Как найти парето оптимальное множество

Множество Парето

Множество Парето содержит точки третьего класса, каждую из которых можно переместить во множестве М лишь при условии уменьшения хотя бы одной из координат.

• Ввод данных
• Решение

С помощью калькулятора среди исходных точек выделяются точки третьего класса, из которых формируется множество Парето.

Операция называется оптимальной по Парето, если не существует операций, которые бы ее доминировали. Соответственно, решение x ∈ Q называется оптимальным по Парето, если не существует решений, которые бы его доминировали.

В случае, если количество Парето-оптимальных решений больше одного, то для определения лучшего решения можно применить:

• взвешивающую формулу f(x,y)=2x-y, если x→max, y→min.
• метод идеальной точки

Применение множества Парето в задачах оптимизации

Считается, что наилучшие решения многокритериальной задачи следует искать именно среди множества Парето. Поэтому построение множества Парето нередко считают первым необходимым шагом в решении любой многокритериальной задачи.

1. Биматричные игры.
2. Метод последовательных уступок.
3. Метод идеальной точки.
4. Анализ доходности и риска финансовых операций.

Примеры

Пример №1

Пример. Необходимо отобрать в множество Парето микросхемы ПЗУ из 10 штук. ПЗУ характеризуются емкостью и быстродействием. На графике наши объекты расположатся следующим образом:

Быстродействие
Емкость

5
7
1
8
2
6
10
9
3
4

Решение. Характеристики ПЗУ Быстродействие и Емкость максимизируются, т.е. чем выше их значение, тем лучше ПЗУ. Рассмотрим ПЗУ5 и ПЗУ1. ПЗУ1 лучше ПЗУ5 по емкости, поэтому ПЗУ5 можно отбросить. Также ПЗУ6 хуже ПЗУ2 по быстродействию и, поэтому в дальнейшем рассматриваться не будет. Наиболее плохими характеристиками обладают ПЗУ7,8,9,10. Из ПЗУ1,2,3,4 нельзя выбрать наилучшее, потому что у каждого из них одна из характеристик (быстродействие или емкость) лучше чем у других, а другая хуже. Эти ПЗУ1,2,3,4 и составляют множество Парето.

Пример №2

Пусть имеется задача с двумя целевыми функциями.

	X1	X2	X3	X4	X5	X6	X7	X8
F1	13	32	17	-3	11	12	2	14
F2	1	5	2	15	9	43	5	11

Требуется найти оптимальные по Парето решения, если целевые функции требуется максимизировать.

Решение. Критерии оптимизации:

x → max, y → max

Операция №2 доминирует над №1,3,7.

Операция №5 доминирует над №7.

Операция №6 доминирует над №4,5,7.

Операция №8 доминирует над №1,5,7.
Загрузка…
Следовательно, операции №2,6,8, оптимальны по Парето.

Операции, оптимальные по Парето, не обязательно являются «самыми лучшими» и даже просто «хорошими» — эти операции не являются худшими.

Пример №3

Инвестор рассматривает четыре инвестиционные операции со случайными эффективностями, описываемыми случайными величинами E1, E2, E3, E4 с рядами распределения:

E1	2	5	8	4
p	1/6	1/2	1/6	1/6

E2	2	3	4	12
p	1/2	1/6	1/6	1/6

E3	3	5	8	10
p	1/6	1/6	1/2	1/6

E4	1	2	4	8
p	1/2	1/6	1/6	1/6

Требуется определить, какие из этих операций оптимальны по Парето.

Решение. Ожидаемые эффективности и риски равны соответственно MЕ₁ = 4.81, σ₁ = 1.77, MЕ₂ = 4.16, σ₂ = 3.57, MЕ₃ = 7.00, σ₃ = 2.30, MЕ₄ = 2.81, σ₄ = 2.54. Нанесем точки (ME_i; σ_i) на единый график (рис.). i-я операция доминирует j-ю, если точка, соответствующая i-й операции, находится на графике правее и ниже точки, соответствующей j-й операции.

Критерии оптимизации:

MЕ → max, σ → min
Загрузка…

Рисунок — График «риск — доходность»

Видно, что первая операция доминирует вторую и четвертую, третья операция также доминирует вторую и четвертую. При этом первая операция не доминирует третью, а третья не доминирует первую. Первая и третья операции, таким образом, оптимальны по Парето.

Если целевая
функция векторная функция векторного
аргумента и каждому малому изменению
переменных Xсоответствует
малое изменение каждого критерия, то
критериальное пространство – это
область с внутренними точками и границей.
(не обязательно замкнутая).. Пусть есть
только два критерияиk₁max;k₂max

Рассмотрим
область возможных значений критериев.
(рис. а). Ясно, что точки, лежащих на одной
вертикали или на одной горизонтали
всегда безусловно сравнимы (см. точки
1,2,3). Получается, что все внутренние
точки можно отсеять. Дуга АВ состоит из
лучших точек по критериюk₂
при постоянномk₁.
Но часть точек дуги АВ , а именно точки
дуги AС можно отбросить, так как они
хуже точек СB. . Поэтому
точками множества Парето будут являться
точки находящиеся на дугеCB.
При анализе характерными являются точки
касания вертикалей и горизонталей к
области критериев (точки А,В,С,D).

Существует несколько
алгоритмов нахождения множества Парето.
Они зависят от того, в каком виде задано
множество вариантов критериев. В
практических задачах сначала приходится
получать само множество критериев,
затем получать множество Парето в
критериальном пространстве и только
затем можно определить Парето -оптимальное
множество в области допустимых решений
X.

Существует два
основных метода нахождения множества
Парето:

1. Метод обхода
   конусом. Этот метод применяется для
   непрерывной области критериев. Назовем
   конусом пространственный угол, образуемый
   лучами, идущими из общей вершины и
   ограниченные в каждой плоскости углом.
   Направление ограничивающих лучей
   соответствует направлению оптимизации
   критериев.

Пусть
для двух критериев:k₁
max( ↑)
и k₂ 
min ( ↓),тогда конус имеет вид:

Для получения
множества Парето достаточно установить
вершину конуса на все точки границы
области критериев, если при этом ни один
луч не пересекает область, то вершина
лежит в точке Парето, а если пересекает,
то нет.

Пример:k₁
→min

k₂
→min

Множество Парето:
[AB](CD]

2.Метод
прямоугольников.Этот метод применяют,
когда критериальное пространство
представляет собой отдельные точки или
табличные значения. Сформулируем
алгоритм для случая двух критериев,
когдаk₁ →minиk₂
→min, а критериальное
пространство – точки на плоскости.

1)Фиксируем самые
левые точки, если их несколько, выбираем
среди них самую нижнюю. Эта точка является
точкой Парето, фиксируем ее.

2)Выберем самую
нижнюю точку, если их несколько, то
выбираем самую левую. Это точка Парето,
фиксируем ее.

3)Через полученные
точки проводим вертикаль и горизонталь.
Отбрасываем сами точки Парето, точки
лежащие на границе полученного
прямоугольника и точки вне прямоугольника.

4)К внутренним
точкам полученного прямоугольника
применяем алгоритм с пункта 1.

Алгоритм
заканчивается тогда, когда внутри
прямоугольника не останется ни одной
точки.

Множество Парето:
1,2,3,4,5,6.

Вышеизложенный
алгоритм легко обобщается на случай
большего числа критериев, при других
направлениях оптимизации, а также на
случай табличного задания критериев.

Соседние файлы в папке Заочники

• #
• #
• #
• #

Вектор методы оптимальных решений

В упрощенном виде задача векторной оптимизации формируется следующим образом:

Имеется n конкурирующих решений:

i> = 1, S₂, . S_n>, т.е. стратегий, структур, проектов, плакатов и т.д. и m частных критериев

j> = 1, K₂, . K_m>, не всегда согласованных между собой и противоречивых.

Для оценки конкурирующих решений по частным критериям используются различные средства: экспертные процедуры, мат. моделирование, натуральные эксперименты. При этом множество конкурирующих решений отображается в матрицу векторных оценок:

S1	S2	.	Sn
[kji] =	k11	k12	.	k1n
k21	k22	.	k1n
.	.	.	.
km1	km2	.	kmn

Исходя из матрицы векторных оценок и системы предпочтений ЛПР выбирается рациональное решение.

E = opt_Sj <[k_ji], система предпочтений ЛПР> следовательно S_rat

opt — некоторый оператор векторной оптимизации.

Выбор рационального решения связан с преодолением неопределенностей, которые имеются в связи с наличием многих критериев. Эта неопределенность является принципиальной. Для ее компенсации есть лишь одна единственная возможность: использование системы предпочтений ЛПР (т.е. дополнительной, субъективной информации).

Использование субъективной информации ЛПР позволяет преодолеть принципиальные трудности и выбрать рациональный критерий.

Все множество методов векторной оптимизации можно разбить на 5 классов.

1. Методы, основанные на формализации, в виде задач математического программирования.
2. Методы, основанные на реинжинировании критериев и их последовательном применении.
3. Методы, использующие обобщенный критерий для сравнительной оценки альтернатив.
4. Методы, не использующие обобщенный критерий для сравнительной оценки альтернатив.
5. Методы, реализующие процессы структуризации и адаптации при выборе рациональных решений.

Методы расположены в порядке возрастания их потенциальной характеристики (классификационный признак — полнота реализации принципа системности). Методы 1-го и 2-го класса не реализуют в полной мере принцип системности. Методы 3-го класса достаточно конструктивны (их легко использовать), однако не всегда удается обосновать и построить обобщенный критерий. Методы 4-го класса более прогрессивны, т.к. они предусматривают активное использование ЛПР в процессе анализа альтернатив. Методы 5-го класса отражают современные тенденции в области векторной оптимизации и находят применение в современных перспективных интерактивных автоматизированных системах.

АСНИ, САПР, АСЛПР, . поддержки принятия решений.

4-5 — разрабатывают (в том числе и на нашей кафедре).

Принцип согласованного оптимума В.Парето

В.Парето обосновал принцип согласованного оптимума, ориентируясь на конфликтную ситуацию между несколькими субъектами с пересекающимися интересами (1870 г). Согласованный оптимум означает преобразование конфликтной ситуации в такую ситуацию, в которой ни один из участников конфликта не может улучшить свое состояние, не причинив своими действиями вреда партнерам. Состояние согласованного оптимума является наилучшим для всех взаимодействующих субъектов. Леонард Заде распространил принцип согласованного оптимума на технические системы (1963 г).

В процессе их проектирования стремятся оптимизировать систему по многим, часто противоречивым критериям. Однако оптимизация системы по одному из критериев практически исключает возможность оптимизации по другим критериям. Поэтому важно найти согласованный оптимум для всех используемых критериев.

Если векторная оптимизация осуществляется с использованием обобщенного критерия, то реализуются обычно следующие процедуры:

1. Выполняется обоснование способа свертки частных критериев в обобщенный критерий.
2. Учитывается важность частных критериев.
3. Векторные оценки приводятся к безразмерному виду.
4. Для всех конкурирующих решений вычисляются обобщенные скалярные оценки.
5. Определяется область компромисса, содержащая парето-оптимальные решения (т.е. такие решения, когда улучшения состояния по каждым из критериев ухудшает состояние по другим критериям).
6. Выбирается рациональное решение в области компромиссов с учетом системы предпочтений ЛПР.

Приемы поиска Парето-оптимальных решений

Пример 1: определить Парето-оптимальные варианты системы

j>	Единица измерения	Направление экстремума	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10
K1 — масса	K2	min	13	5	11	2	10	16	12	15	9	5
K2 — стоимость	рубли	min	200	900	400	800	700	200	500	500	1100	1100

Явно видно, что вариант S₁₀ можно выбросить, т.к. S₂ — дешевле. S₆ — можно забраковать и оставить первый вариант, а остальные сравниваем с оптимальными (т.е. 3, 4 и т.д. с 1 и 2). Найдем граничные варианты в области компромисса: S₁ и S₂, причем варианты S₆ и S₁₀ необходимо отбраковать как худшие.

Определим Парето-оптимальные варианты системы.

Произвести дальнейший отбор.

Пример 2: Определить парето-оптимальные варианты системы, которая состоит из блоков А и В

j>	Единица измерения	Направление экстремума	Блок A	Блок B
A1	A2	A3	A4	A5	A6	B1	B2	B3	B4	B5
K1 — масса	K2	min	6	7	5	17	14	15	10	6	6	15	17
K2 — стоимость	рубли	min	800	600	500	300	200	250	500	400	300	200	300

Определим Порето-оптимальные варианты системы S₁, S₃, S₄

Пример 3: выбрать рациональный вариант системы в условиях, когда ЛПР применяет минимальный критерий

j>	Единица измерения	Направление экстремума	i>
S1	S2	S3	S4	S5	S6
K1 — вероятность отказа	—	min	1,2⋅10 -2	0,5⋅10 -2	0,3⋅10 -2	0,1⋅10 -2	0,08⋅10 -2	0,05⋅10 -2
K2 — затраты ресурсов	тысячи рублей	min	200	400	600	900	1200	1500
Ограничения для системы K1 ≤ 1⋅10 -2 , K2 (M) образует матрицу критерии структуры

j>	Единицы измерения	Направление экстремума	i>
S1	S2	.	Sn
K1	.	.	K11 (M)	K12 (M)	.	K1n (M)
K2	.	.	K21 (M)	K22 (M)	.	K2n (M)
.	.	.	.	.	.	.
Km	.	.	Km1 (M)	Km2 (M)	.	Kmn (M)

Этап 4:

Составляется матрица бинарных предпочтений ЛПР, которое содержит результаты попарных сравнений критериев по важности. 1 — если критерий строки считается более важным, чем критерий столбца. 0 — в противном случае. 0,5 — если критерии не сравнимы по важности.

Суммирование оценок по строке определяет цену критерия.

i>	K1	K2	.	Km	Cj (M)
K1	.	.	.	.	.
K2	.	.	.	.	.
.	.	.	.	.	.
Km	.	.	.	.	.

Вылавливаем, что у ЛПР «в голове»

Этап 5:

Находятся веса частных критериев, отражающие неформальное отношение ЛПР

Этап 6:

Находятся веса частных критериев, исходя из разброса векторных оценок

Этап 7:

Находятся обобщенные веса частных критериев в классе линейных функций

где а и b — это коэффициенты, характеризующие степень доверия к соответствующим весам.

В частном случае, когда a = b = 0,5

Этап 8:

Оценки матрицы критериев структуры приводятся к безразмерному виду.

Δk_j значение-кванты по частному критерию K_j, причем под квантой понимается мера разумной точности измерения соответствующей характеристики.

Этап 9:

Формируется матрица взвешенных оценок

Этап 10:

Вычисляются обобщенные скалярные оценки

т.е. находится разность суммарных взвешенных оценок по критериям, подлежащим соответственно, минимизации и максимизации.

Этап 11:

при оценке структур в диапазоне условий осуществляется η-кратное повторение этапов 3-10. В результате получаем матрицу структуры условий.

i>
1	2	.	η
S1	q1 (1)	q2 (1)	.	q1 (2)
S2	q2 (1)	q2 (2)	.	q2 (2)
.	.	.	.	.
Sn	qn (1)	qn (2)	.	qn (2)

Для первого варианта воздействия

Этап 12

На основе матрицы структуры условия выбирается рациональная структура системы. Эта структура должна обладать приемлемой эффективностью для всех вариантов условий, возникающих с вероятностями p_M. Для известных вероятностей p_M, имеющих частотную или субъективную трактовку, целесообразно использовать критерий максимума средней эффективности в диапазоне условий.

На практике типичной является ситуация, когда вероятности p_M не известны. В данном случае используются критерии для выбора решений в условиях неопределенности.

Структурная оптимизация локальной информационно-вычислительной сети

Применим методику многокритериального выбора рациональных структур, для структурной оптимизации локальной информационно-вычислительной сети (ИВС). Локальная ИВС содержит вычислительную систему, которая может включать несколько однотипных процессоров (на сколько процессоров?) и N распределенных по региону терминалов пользователей, имеющих теледоступ к ИВ ресурсам этой системы.

Необходимо на реальных данных определить число процессоров.

Этап 1: Множество конкурирующих структур

S₁ — структура с одним процессором;

S₂ — структура с двумя процессорами;

S₃ — структура с тремя процессорами.

Этап 2: Совокупность частных критериев

K₁ — время реакции системы;

K₂ — коэффициент загрузки процессора;

K₃ — пропускная способность системы;

K₄ — вероятность правильного ответа;

K₅ — стоимость процессорных устройств.

Этап 3: Матрица критерии структуры:

j>	Единицы измерения	Направление экстремума	N = 10	N = 20	N = 30	N = 50
S1	S2	S3	S1	S2	S3	S1	S2	S3	S1	S2	S3
K1	Сек	min	2,89	2,08	2,05	5,7	2,89	2,71	11,5	4,38	3,38	25,8	9,64	0,99
K2	%	max	55	30	20	91	55	37	99,8	75	51	100	91	63
K3	Задач/сек	max	0,78	0,83	0,83	1,27	1,55	1,57	1,4	2,09	2,15	1,4	2,55	2,69
K4	—	max	0,85	0,95	0,99	0,85	0,95	0,99	0,85	0,95	0,99	0,85	0,95	0,99
K5	Тыс. руб.	min	340	490	640	340	490	640	340	490	640	340	490	640

Чтобы получить количественные средства, нужно использовать все возможные средства (например, аналитические вычисления).

Покажем расчеты для N = 20

i>	K1	K2	K3	K4	K5	Cj
K1	1	0,5	0	0,5	2
K2	0	0,5	0	0	0,5
K3	0,5	0,5	0	0	1
K4	1	1	1	0,5	3,5
K5	0,5	1	1	0,5	3

Этап 6: Веса частных критериев исходя из разброса векторных оценок для N = 20

суммируем по строке 3

i>	Kji^	rj	ϑ2j
K1	3,77	0,34	0,33
K2	61	0,33	0,32
K3	1,46	0,09	0,09
K4	0,93	0,06	0,06
K5	490	0,2	0,2

0,34 = (/5,7 — 3,77/ + /2,89 — 3,77/ + /2,71 — 3,77/3,77)/3

Наибольший вес в формальном способе расчета имеет время реакции системы. Далее — все наоборот (не так, как дал человек).

Этап 7: Усредненные веса частных критериев для N = 20

ω₁ = 0,27( = 0,265) а = b = 0,5

ω₂ = 0,18 Наиболее важным получился критерий K₁

Этап 8: Матрица безразмерных векторных оценок для N = 20

j>	ΔKj	Единица измерения	i>
S1	S2	S3
K1	0,5	Сек	11,4	5,78	5,42
K2	5	%	18,2	11	7,4
K3	0,25	Задач/сек	5,08	6,2	6,28
K4	0,1	—	8,5	9,5	9,9
K5	100	Тыс. руб.	3,4	4,9	6,4

т.е. делим на кванту то число, которое стоит в таблице матрицы критериев структуры

Кванта — это тот «кирпичик», через который человек чувствует этот критерий 0,5 — т.е. через 0,5 сек человек начинает чувствовать эту характеристику.

Этап 9: Матрица взвешенных векторных оценок для N = 20

j>	ωj	Направление экстремума	i>
S1	S2	S3
K1	0,27	min	3,08	1,57	1,46
K2	0,18	max	3,28	1,98	1,33
K3	0,09	max	0,46	0,51	0,57
K4	0,21	max	1,78	1,99	2,03
K5	0,25	min	0,85	1,22	1,6

Эти веса умножаем на столбик прошлой матрицы

Этап 10: обобщенные скалярные оценки для N = 20

Этап 11: матрица структуры условия:

i>
N = 10	N = 20	N = 30	N = 50
S1	2,75	1,59	-3,27	-12,27
S2	1,63	1,74	0,81	-1,9
S3	0,3	0,92	0,24	-2,29

Мы провели расчеты для случая гот.

1,74 — наиболее предпочтителен для случая с 20-тью терминалами.

Этап 12: Эффективность конфигурирующих структур в диапазоне условий

i>		E
P(10) = 0,1	P(20) = 0,5	P(30) = 0,3	P(50) = 0,1
S1	0,27	0,79	-0,98	-1,23	-1,15
S2	0,16	0,87	0,24	-0,19	1,08
S3	0,08	0,46	0,07	-0,23	0,38

Суммируем по строке — т.е. эффективность в данном диапазоне условий;

Умножаем вероятности на прошлую матрицу

Р(10) — т.е. вероятность подключения 10-ти терминалов

Видим, что 2-й вариант системы является предпочтительнее

Это решение дают ЛПР.

Вывод: в заданных условиях рациональной является структура S₂

Постановка задачи векторной оптимизации

1. Постановка задачи векторной оптимизации

Все рассмотренные в предыдущих разделах оптимизационные задачи имели всего один критерий оптимальности, а модели их описывающие были однокритериальными. Теория моделирования однокритериальных задач оптимизации и их решения представляет собой предмет рассмотрения математического программирования, и достаточно глубоко проработана.

В реальных задачах выбора наиболее предпочтительного решения, возникающих на практике, как правило, присутствуют несколько критериев оптимальности. Можно привести много примеров, когда требуется найти решение, для которого достигались наилучшие значения сразу по нескольким критериям. Наиболее распространенная задача, которую мы решаем очень часто (не облекая ее в термины оптимизации) — это поиск покупки, которая была как можно качественнее и как можно дешевле.

Задачи выбора некоторого решения из множества допустимых решений с учетом нескольких критериев оптимальности называют многокритериальной задачей оптимизации.

Многокритериальные задачи широко распространены в техническом проектировании, например, задача проектирования компьютера с максимальным быстродействием, максимальным объемом оперативной памяти и минимальным весом или задача проектирования электрического двигателя с максимальной мощностью, максимальным коэффициентом полезного действия, минимальным весом и минимальными затратами электротехнической стали (естественно, при ограничениях на необходимые параметры проектируемых устройств). Реальные многокритериальные управленческие задачи также широко распространены, лозунг экономики СССР 80-х гг. — «максимум качества при минимуме затрат», несмотря на его одиозность, выражал сущность большинства проблем управления.

Под многокритериальной задачей зачастую понимают не собственно вербальное описание задачи, а ее модель, а именно: «многокритериальная задача – математическая модель принятия оптимального решения по нескольким критериям. Эти критерии могут отражать оценки различных качеств объекта или процесса, по поводу которых принимается решение».

Формально многокритериальная задача как модель задается в виде:

, (5.1)

где D — множество допустимых решений. F(x) – векторная функция векторного аргумента x, которую можно представить как F(x)=, где f1(x), f2(x), … , fk(x) – скалярные функции векторного аргумента x, каждая их которых является математическим выражением одного критерия оптимальности. Так как в данной модели используется векторная целевая функция, ее зачастую называют задачей векторной оптимизации. Очевидно, что задача (5.1) не принадлежит классу задач математического программирования, т. к.модели этого класса задач содержат всегда только одну целевую функцию векторного аргумента.

Иначе задачу (5.1) можно переписать в виде:

Сущность поставленной задачи состоит в нахождеии такого ее допустимого решения, т. е. >, которое в том или ином смысле максимизирует (минимизирует) значения всех целевых функций fi(x), i=1,k. Существование решения, буквально максимизирующего все целевые функции, является редким исключением. (Если вспомнить пример о поиске одновременно очень качественной и очень дешевой покупки, то становится понятным, что нахождение такого решения – редкая удача, но, гораздо более часто, это неразрешимая задача).

Отсюда следует, что принципиальным моментом при решении такого рода задач является предварительная договоренность, а что считать самым предпочтительным решением, т. е. надо договориться об используемом принципе оптимальности. Ранее используемый принцип оптимальности «хорошо то, что доставляет наибольшее (наименьшее) значение имеющемуся единственному критерию оптимальности» в многокритериальных задачах очевидно «не работает».

Задача векторной оптимизации в общем случае не имеет строго математического математического решения. Для получения того или иного ее решения необходимо использовать дополнительную субъективную информацию специалиста в данной предметной области, которого принято называть лицом принимающим решение (ЛПР), в английском языке — decision maker. Это означает, что при решении задачи разными специалистами с привлечением различных источников информации, скорей всего будут получены различные ответы.

Задачи векторной оптимизации, в настоящее время принято рассматривать в рамках теории принятия решений, основной особенностью задач которой является наличие неопределенности. Эта неопределенность не может быть исключена с помощью различных приемов моделирования и объективных расчетов. В многокритериальных задачах неопределенность состоит в том, что неизвестно, какому критерию отдать предпочтение и в какой степени. Для устранения этой неопределенности необходимо, во-первых, сформулировать специальный принцип оптимальности, а также привлечь дополнительную субъективную информацию ЛПР, основанную на его опыте и интуиции.

2. Основные определения теории векторной оптимизации. Принцип Парето

Введем несколько определений.

Пусть решается задача (6.1) и есть x‘, x» — допустимые решения данной задачи. Говорят, что x‘ более предпочтительное решение по сравнению с x», если f i (x‘) ≥ f i (x») i=1,k), причем i0, такой, что f i (x‘) > f i (x»). Другими словами, будем считать, что решение x’ более предпочтительно по сравнению с решением x» , если оно не хуже x» по всем рассматриваемым критериям, причем среди всех критериев есть хотя бы один критерий с номером i0, для которого решение x‘ лучше, чем x»

Некоторое решение x* задачи (5.1) называется эффективным решением данной задачи, если для него не существует более предпочтительных решений. Иначе можно сказать, что эффективным решением называется такое решение x*, которое нельзя улучшить по какому-либо из критериев, не ухудшив при этом значения других критериев.

Множество эффективных решений называется множеством Парето и обозначается P(D). Очевидно, множество Парето является подмножеством множества допустимых решений, которое, в свою очередь принадлежит n-мерному векторному пространству, т. е. P(D) D En.

Вектор значений критериев, вычисленных для эффективного решения F(x*), называется эффективной оценкой. Совокупность всех эффективных оценок, т. е. образ множества Парето в пространстве критериев, называется множеством эффективных оценок и, как правило, обозначается как F (P). Множество эффективных оценок является подмножеством образа множества допустимых решений в пространстве критериев F(D), которое, в свою очередь, является подмножеством k-мерного векторного пространства, т. е. F(P) F(D) Ek. Т. е. можно сказать, что множеству Парето P, принадлежащему множеству допустимых решений D, с помощью векторной функции F сопоставлется множество эффективных оценок F(P)

Решение xl называется слабоэффективным решением задачи (6.1), если для него не существует решения xll такого, что i=1,k f(xl) > f(xll), другими словами, слабоэффективное решение – решение, которое не может быть улучшено одновременно по всем критериям.

P(D)En.

Введение понятия слабоэффективных решений вызвано тем, что в процессе оптимизации часто получаются решения, принадлежащие S(D) (множеству слабоэффективных решений), но не являющиеся эффективными. Такие решения представляют, конечно, меньший интерес по сравнению с эффективными решениями.

Субоптимальное решение (по критерию fi(x) – оптимальное решение многокритериальной задачи, найденное по какому-либо одному критерию (i-ому) без учета остальных критериев.

Принцип Парето: смысл введенного понятия эффективного решения состоит в том, что оптимальное решение следует искать только среди элементов множества Парето — множества P(D). В противном случае всегда найдется точка x, оказывающаяся более предпочтительной независимо от расстановки приоритетов и относительно важности отдельных частных критериев.

Принцип Парето позволяет сузить класс возможных претендентов на окончательное решение и исключить из рассмотрения заведомо неконкурентноспособные варианты. А окончательный выбор осуществляется на основе дополнительной информации о предпочтении лица, принимающего решения.

Рассмотрим введенные понятия на примере.

С помощью графического метода найдем субоптимальные решения (см рис. 5.1). По критерию f1 — это точка Е(2,0), f1(Е)=6.

По критерию f2 субоптимальные точки — это точки отрезка, соединяющего точки С(0,4) и В(1,4),], при этом f2(С) = f2(В)=4

Таблица 5.1 – Анализ точек множества D примера 6.1 на принадлежность множеству Парето

Не улучшаемые точки

Улучшаемая по 1-му критерию

Одновременно улучшаемая по

В таблице 5.1 приведены значения целевых функций f1(x)= 3x1—x2 и f2(x)= x2 для всех точек, обозначенных на рис. 5.1. На основании этих данных построен рис. 5.2. Полученный многоугольник F(C) F(K) F(E) F(A) F(G) F(B) является отображением многоугольника допустимых решений примера C K E A G B в пространсте критериев.

3. Нормализация критериев

Зачастую целевые функции fi(x) имеют различную размерность и их необходимо свести к безразмерному виду с помощью какого-нибудь преобразования. Это преобразование должно удовлетворять по крайней мере следующим критериям:

· иметь общее начало отсчета и один порядок изменения значений на всем множестве допустимых решений

· быть монотонным преобразованием, т. к. должно сохранять отношение предпочтения на множестве D, т. е. не менять множество Парето

· учитывать необходимость минимизации отклонения от оптимальных значений по каждой целевой функции.

Обыкновенно для получения нормализованных критериев в качестве таких преобразований используют следующие:

где , как правило, полагают ; , — наибольшее и наименьшее значения i-го критерия (нибольшая и наименьшая эффективная оценка) соответственно. Причем , т. е. минимизируется разность между искомым решением и субоптимальным.

Пример 5.1 (продолжение 1)

Если принять преобразование для нормализации критериев вида:

то первый нормализованный критерий получается в виде:

.

И тогда можно рассчитать значение первого нормализованного критерия в наилучшей и наихудшей точках по критерию f1:

Второй нормализованный критерий получается в виде: . А значение второго нормализованного критерия в наилучшей и наихудшей точках по критерию f2:

.

График, построенный по значениям нормализованных критериев, вычисленных для выше перечисленных точек (см табл. 5.1) представлен на рис. 5.3. Нижняя ломаная полученного многогранника есть множество нормализованных эффективных оценок.

Рисунок 5.3- Иллюстрация процесса решения примера 5.1 в пространстве нормализованных критериев.

4. Решение многокритериальных задач методом ограничений. Компромиссное решение

Недостаток принципа Парето в том, что он предлагает в качестве решения – множество решений, что не всегда приемлемо. Для того, чтобы выбрать из этого множества единственное решение нужны какие-то дополнительные сведения, предположения, договоренность о том, что же считать наилучшим решением (некоторая дополнительная неформальная информация).

Естественно, следует считать наилучшим такое решение, при котором величина отклонений от оптимальных значений по каждой целевой функции достигает своего минимального значения, т. е. для преобразованных функций – такое решение, при котором . Но наименьшие значения величин или (x) , как правило, не достигаются одновременно ни для какого решения из D (т. е. нельзя подобрать x, чтобы (x) max или min min .

Поэтому нужны какие-то дополнительные процедуры для отыскания какого-то единственного представителя из множества Парето. Специфика решения таких задач состои в том, что сам выбор такой процедуры, метода нахождения окончательного решения в какой-то степения основан на предположениях ЛПР, т. е. на субъективной информации.

Метод ограничений, рассматриваемый в данном разделе, предназначен для отыскания так называемого компромиссного решения, т. е. такого эффективного решения для которого взвешенные относительные потери (потери в смысле разности возможного наилучшего значения целевой функции и значения этой функции для данного – компромиссного — решения) минимальны и равны между собой.

Метод ограничений основан на теореме: если x0 – эффективное решение для данного вектора предпочтений , то ему соответствует наименьшее значение , при котором система равенств

= выполняется для всех i=1,k (5.2)

При этом под вектором предпочтений =понимается некоторый вектор весовых коэффициентов. Как правило, на него накладываются ограничения . С помощью весовых коэффициентов задаются определенные ЛПР предпочтения (значимость) целевых функций (критериев) друг перед другом, выраженные в количественной шкале.

Например, если принять и , то это означает, что по информации ЛПР первый критерий в 2 раза значимее по сравнению со вторым.

Тогда в качестве решения задачи (5.1) можно принять компромиссное решение с заданным вектором предпочтений. Очевидно, что компромиссное решение – это такое эффективное решение x0, которое обеспечивает одинаковые минимальные значения параметра , при котором система (5.2) совместна.

Таким образом, компромиссное решение может быть найдено как единственное решение системы неравенств вида

для минимального значения параметра , при котором эта система совместна.

Как уже говопилось, метод отыскания эффективного решения, основанный на этом положении, называется методом ограничений. Этот метод можно предполагает необходимость решения вспомогательной минимаксной задачи:

(5.3)

Для того, чтобы избежать необходимости использовать минимаксный (нелинейный) критерий, вспомогательную задачу (5.3) можно преобразовать в адекватную задачу (5.4), но уже с линейной целевой функцией.

(5.4)

Если исходная задача (5.1) является задачей представлена с помощью линейных целевых функций и функций-ограничений, то вспомогательная задача (5.4)является задачей ЛП:

(5.5).

Пример 5.1 (продолжение 2)

Выше были построены нормализованные критерии для целевых функций примера 5.1: 1(x)=0.6-0.3+0.1, 2(x)=1-0.25. Тогда система вновь введенных ограничений вспомогательной задачи (5.5) при будет выглядеть как:

.

Вспомогательная задача для этого примера представляет собой задачей ЛП с тремя неизвестными и функциональными ограничениями:

Для решения вспомогательной задачи строим симплекс-таблицы:

—

—

—

—

—

—

=

=

=

=

=

=

=

=

=

=

Векторные интерпретация и метод решения задачи линейного программирования Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Щеглов А. Ю.

Рассматривается интерпретация задачи линейного программирования как пошаговой задачи многокритериальной оптимизации. Приводится векторная интерпретация аддитивного критерия оптимальности как приведенной длины проекции вектора варианта на идеальный вектор качества в пространстве критериев, откуда вводится векторная интерпретация задачи линейного программирования. Рассматривается метод решения задачи в рамках приведенной векторной интерпретации.

Похожие темы научных работ по математике , автор научной работы — Щеглов А. Ю.

Текст научной работы на тему «Векторные интерпретация и метод решения задачи линейного программирования»

Федеральный портал «Инженерное образование»

Электронный журнал и

#3 март 2006 Ред. совет Специальности Рецензентам Авторам English Koi-8 Win

Векторные интерпретация и метод решения задачи линейного программирования #3 март 2006

А. Ю. Щеглов, д-р техн. наук проф., СПб ГИТМО (ТУ)

Векторные интерпретация и метод решения задачи линейного программирования

Рассматривается интерпретация задачи линейного программирования как пошаговой задачи многокритериальной оптимизации. Приводится векторная интерпретация аддитивного критерия оптимальности как приведенной длины проекции вектора варианта на идеальный вектор качества в пространстве критериев, откуда вводится векторная интерпретация задачи линейного программирования. Рассматривается метод решения задачи в рамках приведенной векторной интерпретации.

Интерпретация задачи линейного программирования как пошаговойзадачи

Задача линейного программирования в общем виде может быть представлена следующим образом: найти X n = 1, . N, такие, что

при условии, что

при Хп ^ 0, п = 1, . N. При необходимости дополняется условие целочисленности всех Хп.

Рассмотрим интерпретацию задачи линейного программирования как пошаговую задачу многокритериальной оптимизации. В общем случае задача многокритериальной оптимизации может быть сформулирована следующим образом. Задано N вариантов системы с номерами п = 1, . N, каждый из которых характеризуется М параметрами (или частными критериями качества) дпт с номерами т = 1, . М. Требуется выбрать вариант,

превосходящий остальные варианты по совокупности параметров. В качестве критерия оптимальности (или агрегатирующего показателя качества) на практике, как правило, используется аддитивная свертка нормированных значений параметров

где дпт — по какому-либо правилу нормированные (приведенные к безразмерному виду)

значения разнородных параметров. В случае необходимости учета различной относительной важности параметров в формуле (1) используются коэффициенты относительной важности параметров (или весовые коэффициенты) вт, где 0 ^ вт ^ 1,

тах, —>тт з что имеет физический

смысл выбора нехудших решений, качество которых в М-мерном пространстве отображается векторами, имеющими максимальную длину и наилучшим образом совпадающими по направлению с заданным идеальным вектором.

Данный подход, наряду с методом Паретто, представляет чисто теоретический интерес, так как на практике использование обоих критериев оптимальности существенно усложняет задачу оптимизации и, как правило, позволяет найти множество «нехудших решений», практически не уступающему по величине исходному множеству сравниваемых альтернатив. В [4—9] в качестве критерия оптимальности нами предлагается использовать параметр «длина проекции вектора качества варианта на идеальный вектор» Хп0, который

позволяет одновременно учитывать оба параметра X и , т. е. свести задачу

оптимизации к однокритериальной

при условии выбора оптимального варианта Хц

* глах . В [4] строго доказывается, что в

ортонормированном базисе вместо длины проекции на идеальный вектор может рассматриваться аддитивная свертка нормированных значений параметров, представляющая собой сумму нормированных параметров вариантов, использование которой существенно упрощает решение задачи при векторной ее интерпретации.

Действительно, с учетом того, что в ортонормированном базисе нормированные значения параметров идеального вектора = 1, т = 1. М, подставляя (2) и (3) в (4),

соответственно из (1) имеем

откуда следует, что аддитивная свертка параметров представляет собой приведенную или

умноженную на коэффициент (М) длину проекции вектора качества варианта на вектор

качества идеального варианта в ортонормированном пространстве критериев ЕМ. Так как

значение (М)1 совпадает для всех вариантов, т. е. не влияет на результат сравнительного анализа, будем считать, что критерий оптимальности задается формулой (1) и имеет физический смысл длины проекции вектора качества варианта на идеальный вектор качества.

Теперь остановимся на вопросах синтеза ортонормированного базиса и векторной интерпретации использования весовых коэффициентов вт. При объективном способе

нормирования параметров [4, 9] в качестве идеальных выбираются лучшие значения параметров на сравниваемом множестве вариантов п = 1. N, задаваемые в рассматриваемом случае формулой

причем на сравниваемом множестве вариантов п = 1. N корректируются значения параметров, качество которых превосходит задаваемое (или требуемое) идеальное — приравнивается задаваемому идеальному. Нормированные значения параметров задаются формулами

Задание весовых коэффициентов может быть интерпретировано следующим образом: изменение весовых коэффициентов параметров изменяет направление и длину гипотетически идеального вектора в пространстве критериев. При этом изменяются и длины проекций векторов вариантов на идеальный вектор, т. е. значения аддитивного критерия оптимальности.

Теперь, с учетом предложенной интерпретации задачи линейного программирования как пошаговой многокритериальной задачи оптимизации, для которой, в свою очередь, нами дана векторная интерпретация (в частности, предложена векторная интерпретация аддитивного критерия оптимальности), рассмотрим векторную интерпретацию задачи линейного программирования. Векторная интерпретация задачи на

плоскости (в пространстве Ям = 2) проиллюстрирована на рис. 1.

Рис. 1. Иллюстрация векторной интерпретации задачи линейного программирования

Здесь по осям координат, где откладываются параметры для различных вариантов плана цт, отложены и ограничения Qm. В приведенной системе координат получаем вектор

, образующий идеальное направление «продвижения в пространствеев» для выполнения заданных ограничений (идеальность направления соответствует равенству Qm

в исходной системе ограничений). Два возможных плана (Ы = 2) отображаются в рассматриваемом пространстве векторами, например и . Метод поэтапного

получения оптимального плана (векторный метод планирования) состоит в выборе на каждом этапе оптимизации лучшего вектора по критерию длины проекции вектора варианта на идеальный вектор (00′) с переносом системы координат в направлении и на величину выбранного на очередном этапе оптимизации вектора. В частности, на рис. 1 лучшим для рассматриваемого этапа составления плана при наличии двух вариантов будет вариант, отображаемый вектором . Отложив этот вектор, получим новую систему

координат и соответствующий ей новый идеальный вектор (0*0′), который примем в качестве вектора, задающего идеальное направление для следующего этапа. Многоэтапная процедура завершается при выполнении ограничений по всем видам задач. Набор отложенных векторов на всех этапах оптимизации (и соответственно отображаемые ими возможные частные планы) и составляют оптимальный план.

Замечание. При альтернативной постановке задачи линейного программирования — найти Х п = 1. N, такие, что

при условии, что

необходимо, наоборот, достигнуть разрешенной области за максимальное число шагов. Здесь критерием оптимальности также остается параметр , но условием выбора

оптимального плана уже будет —>min min для каждого этапа оптимизации, причем

оптимизация будет заканчиваться выполнением предпоследнего шага — на последнем вектор пересечет запретную область.

Таким образом, на каждом шаге выбора оптимального плана в качестве критерия оптимальности используется аддитивная свертка нормированных значений параметров

где нормированные значения параметров определяются по формуле

а весовые коэффициенты используются для того, чтобы учесть различие ограничений Qm.

Очевидно, что приоритет планов здесь определяется приоритетами (в данном случае — значениями) ограничений и значениями коэффициентов Сп в целевой функции.

Предположим, что величины Сп = 1 для всех N рассматриваемых вариантов. В данных

предположениях имеем следующую формулу для расчета весовых коэффициентов:

Именно это условие нами рассматривалось при использовании предлагаемого подхода для решения систем линейных уравнений большой размерности [2] и для приложений задач линейного программирования, используемых для решения задачи распределения работ в мультипроцессорных системах, решаемых в рамках теории расписаний [1]. При различии значений С;? аддитивным критерием ^ должно учитываться и различие величин Сп в том смысле, в какой мере по сравнению с вариантом,

увеличит значение целевой функции любой иной п-й вариант. С

учетом сказанного имеем

шах . Формальным условием окончания выполнения пошаговой процедуры оптимизации будет выполнение условия Qm: = 0, т = 1. М.

Решением задачи будет множество вариантов (оптимальный план), соответствующих отложенным на всех шагах оптимизации оптимальным векторам.

Из приведенных формул для расчета параметров оптимизации делаем вывод, что рассматриваемый метод легко реализуем на ЭВМ, а формулы характеризуются низкой сложностью вычислений; все вычисления сведены к пошаговому алгоритму.

Скажем несколько слов относительно вычислительной сложности предлагаемого метода. Следуя тому, что решаемая задача может быть отнесена к N^,-полным, сложность методов, предназначенных для ее решения, оценивается из следующих соображений. Если обозначить через О сложность отдельных операций (вычитание, сложение, деление и т. д.), реализуемых на каждом шаге оптимизации I, I = 1. Ь, причем на каждом шаге требуется выполнить О< операций, вычислительная сложность £ численного метода определяется по

Сформулируем утверждения, доказывающие минимальную вычислительную сложность предложенного векторного метода.

Утверждение 1. Предлагаемый метод позволяет проводить оптимизацию за минимальное число шагов Ь.

Доказательство этого утверждения следует из того, что на каждом шаге выбирается оптимальный вариант, позволяющий наилучшим образом продвигаться в сторону допустимой области, что минимизирует число шагов Ь.

Замечание. Возможность уменьшения числа шагов состоит в том, чтобы не исходно задавать дискретное значение параметра Х например, принимать для каждого шага Хп =

1, а выбирать Хп таким, при котором п-решение для рассматриваемого шага остается

оптимальным. Эта идея заложена, например, в симплекс — алгоритме, что не позволяет рассматривать этот метод как метод комбинаторного программирования. Аналогичный подход может быть применен и в рамках предложенного нами векторного метода [2]. Однако данные подходы приводят к резкому увеличению О, а как следствие, что видим из

(6), и к резкому возрастанию параметра £ (как правило, на каждом шаге оптимизации здесь уже требуется решать системы уравнений). Кстати говоря, именно поэтому в основе разработки численных методов оптимизации лежит идея уменьшения вычислительной сложности отдельного шага, несмотря на возможность увеличения их числа.

Утверждение 2. Предлагаемый метод позволяет проводить сравнительный анализ вариантов на каждом 1-м шаге с минимальной вычислительной сложностью О

Доказательство этого утверждения, рассматриваемое в [4—9], основано на том, что, во-первых, опарное сравнение вариантов на каждом шаге осуществляется только по одному параметру (а не по М), что существенно снижает трудоемкость каждого шага О,,

во-вторых, именно сравнение по одному параметру позволяет выбирать на каждом шаге не ограниченное множество «нехудших решений», а лучший вариант (в противном случае выражение (6) должно было бы учитывать, что на каждом шаге сложность вычислений не О1, а г О, где г, — число «нехудших решений» на 1-м шаге, причем значение г, должно в

прогрессии увеличиваться при переходе к последующим шагам). Однако, платой за сведение задачи к однокритериальной является необходимость нормирования параметров и использование более сложных агрегатирующих критериев оптимальности. Нам удалось минимизировать сложность критерия оптимальности, дав его векторную интерпретацию и сведя задачу к возможности применения аддитивной свертки (кстати говоря, именно поэтому данный вопрос нами был ранее исследован столь подробно). Таким образом, » платой» за возможность сведения задачи к однокритериальной, что существенно упрощает вычисления (в десятки и сотни раз — в зависимости от размерности задачи), можно считать необходимость нормирования, реализуемого на каждом шаге единожды по достаточно простой формуле.

С учетом сказанного можем утверждать, что по параметру £, характеризующему вычислительную сложность численных методов, предназначенных для решения задач, относящихся к классу NP-полных, предложенный в работе векторный метод оптимизации обладает минимальной сложностью.

Таким образом, к достоинствам предлагаемого векторного метода решения задач линейного программирования можно отнести следующее:

• обеспечивает выбор оптимального плана на каждом шаге оптимизации (что гарантирует необходимость выполнения минимального числа шагов при синтезе планов);

• отличается простотой решения задачи в ее целочисленной постановке (на каждом шаге полностью откладывается вектор качества, что соответствует одной единице выбранной работы в оптимальном плане).

Численный метод точного решения задачи

Некоторые из приложений рассматриваемой задачи требуют либо точного ее решения, либо решения с заданной точностью. Для точного решения задачи и решения ее с заданной погрешностью результата может быть предложен двухэтапный подход (предложенный для решения системы линейных уравнений большой размерности в [2]). На первом этапе задача решается целочисленно, где оптимальные векторы откладываются полностью. На втором этапе реализуется точное решение. При этом решение получается уже в системе координат, получаемой для противоположного квадранта, вершиной которой будет точка пересечения последнего отложенного на первом этапе вектора с допустимой областью. Идеальный вектор получаем, соединяя вершину координат с точкой т = 1. М). Повторяем процедуру оптимизации, но уже откладываем некоторые

части к, к . Совместим области

допустимых решений и оптимальные векторы для различных целевых функций в одной системе координат, что приведено на рис. 3. Очевидно, что вектор , но уже

соответственно для второй целевой функции. Другими словами, если в качестве идеального вектора взять, например, вектор и с ним пошагово решить задачу

оптимизации, то многокритериальная задача будет решена при попадании в допустимую область и вектора, откладываемого на последнем шаге. Однако относительно

полученного решения можно утверждать следующее: оно оптимально для первой целевой функции и крайне неудовлетворительно для второй. То же самое можно сказать и о векторе .

Рис. 3. Иллюстрация векторной интерпретации многокритериальной задачи линейного программирования на плоскости

Таким образом, получаем задачу линейного программирования, определяемую в рассматриваемом случае допустимой областью решений и в ортонормированном базисе, являющейся объединением областей и и и2, и бесконечным множеством идеальных

векторов, что проиллюстрировано на рис. 4. Вместе с тем на рис. 3 и рис. 4 явно выделяется один вектор — вектор , характеризуемый тем, что если его

рассматривать в качестве идеального, то его длина совпадает для обеих целевых функций. Другими словами, если вектор рассматривать в качестве идеального, то получаемое

оптимальное решение характеризуется равной степенью оптимальности для различных целевых функций (не являясь в общем случае оптимальным ни для одной из целевых функций в отдельности, так как длина вектора превосходит длину вектора . Такое решение будем называть равнооптимальным, а вектор

равноидеальным. В случае выбора равноидеального вектора задается равная важность целевых функций. При задании в качестве идеального вектора, идеального для конкретной целевой функции, максимально учитывается важность именно этой целевой функции. В общем случае, чтобы учесть более высокую относительную важность какой-либо целевой функции, необходимо в качестве идеального выбрать вектор, расположенный между равноидеальным вектором и вектором, идеальным для этой целевой функции (эти векторы являются граничными), которых, как следует из рис. 4, бесконечное множество. Сказанное является векторной интерпретацией и собственно методом учета относительной важности целевых функций для многокритериальных задач линейного программирования.

Рис. 4. Иллюстрация задания идеального вектора для многокритериальной задачи

Таким образом, многокритериальная задача линейного программирования решается так же, как и однокритериальная, с использованием пошагового метода. Отличие состоит исключительно в способе задания идеального вектора. Равноидеальный вектор определяется по следующей формуле:

учет же относительной важности целевой функции реализуется рассмотренным методом эвристически, например, на основе экспертных оценок.

В заключение отметим, что в работе представлен новый подход к интерпретации и решению задач линейного программирования. Учитывая простоту вычислительных операций, реализуемых при векторной интерпретации задачи как при условии целочисленности переменных, так и без такого условия, и простоту разработанного алгоритма пошаговой оптимизации в целом, можно надеяться на широкое использование метода в задачах оперативного планирования — в условиях жестких временных ограничений на продолжительность синтеза плана, в частности, для распределения работ в проблемно ориентированных вычислительных системах и ЛВС.

1. Щеглов А. Ю. Методика планирования распределения ресурсов вычислительной сети // Автоматика и вычислительная техника, 1989. № 1. С. 39—41.

2. Щеглов А. Ю. Векторная интерпретация и численный метод решения системы линейных уравнений // Изв. ВУЗов. Приборостроение, 1993. № 9—10. С. 36—44.

3. Кузьмин Б. И., Русин Ю. С. Векторная оптимизация систем и аппаратуры радиосвязи // Электросвязь, 1986. № 5. С. 30-32.

4. Щеглов А. Ю. Методика векторной оптимизации сложных подсистем информационно-вычислительных сетей // Автоматика и вычислительная техника, 1988. № 5. С. 14—19.

5. Щеглов А. Ю. Дополнительный критерий для формального выбора оптимального варианта ЛВС из множества «нехудших решений» // Автоматика и вычислительная техника, 1991. № 4. С. 39—41.

6. Щеглов А. Ю. Метод многокритериальной оптимизации сложных систем с экспертным заданием гипотетически идеального вектора качества // Изв. ВУЗов. Приборостроение, 1994. Т. 37. С. 21-23.

7. Щеглов А. Ю. Метод ограничений для оптимизации сложных систем // Радиотехника, 1993. № 4. С. 9—13.

8. Щеглов А. Ю. Метод поинтервального учета неравнозначности разнородных параметров альтернативных вариантов сложных систем вычислительной техники //

Автоматика и вычислительная техника, 1990. № 6. С. 10—13.

9. Щеглов А. Ю. Статистический метод нормирования и учета относительной важности разнородных параметров для многокритериальной оптимизации сложных радиотехнических систем // Радиотехника, 1995. № 3. С. 7—8.

МЕТОДЫ ОПТИМИЗАЦИИ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 8, 1998

Ключевые слова: Линейное программирование, многокритериальная оптимизация, векторное планирование, пошаговые методы.

Публикации с ключевыми словами: Линейное программирование -многокритериальная оптимизация — векторное планирование — пошаговые методы

Публикации со словами: Линейное программирование -многокритериальная оптимизация — векторное планирование — пошаговые методы См. также:

■ Векторный метод решения задачи линейного программирования; с пошаговым усечением множества «нехудших решений» Написать комментарий >>

источники:

http://pandia.ru/text/78/259/32294.php

http://cyberleninka.ru/article/n/vektornye-interpretatsiya-i-metod-resheniya-zadachi-lineynogo-programmirovaniya

Содержание:

Введение

Почти всякая сложная практическая задача принятия решения индивидуального (а тем более группового) является многокритериальной.

Концепция принятия решения в качестве первичного элемента деятельности рассматривает решение как сознательный выбор одного из ряда альтернатив, называемых, в зависимости от их конкретного содержания, стратегиями, планами, вариантами и т.д. Этот выбор производит лицо, принимающее решение и стремящееся к достижению определенных целей. В роли такого лица выступают отдельные люди (группы людей), обладающие правами выбора решения и несущие ответственность за его последствия.

Применение математических методов при принятии решений предполагает построение подходящей математической модели, формализовано представляющей проблемную ситуацию, т.е. ситуацию выбора решений. Для задач принятия решений (задач оптимизации) в условиях определенности, когда случайные и неопределенные факторы отсутствуют, компонентами такой модели являются множество всех (альтернативных) решений, из которых и делается выбор одного наилучшего, или оптимального решения, и описание предпочтений лица, принимающего решение. Для того чтобы была обеспечена возможность выбора, множество должно содержать не менее двух решений.

Методы решения задач математического программирования с одним критерием интенсивно разрабатывались последние 40 лет. Изучение таких методов, однако, отражало самый ранний и простой этап в развитии математического программирования. Жизнь оказалась значительно сложнее. По мере того как мы постепенно вступаем в век информатики, становится ясно, что практически любая серьезная реальная задача характеризуется больше чем одним критерием. Лица, принимающие решения (ЛПР), в значительно большей степени, чем когда бы то ни было, ощущают необходимость оценивать альтернативные решения с точки зрения нескольких критериев.

Результаты исследования задач планирования и управления показывают, что в реальной постановке эти задачи являются многокритериальными. Так, часто встречающееся выражение «достичь максимального эффекта при наименьших затратах» уже означает принятие решения при двух критериях. Оценка деятельности предприятий и планирования как системы принятия решений производится на основе более десятка критериев: выполнение плана производства по объему, по номенклатуре, плана реализации, прибыли по показателям рентабельности, производительности труда и т.д.

Актуальность курсовой работы: исследование сущности оптимальности по Парето.

Цель курсовой работы — исследование сущности оптимальности по Парето, а также того, что можно предпринять, чтобы более эффективно принимать решения.

Для достижения поставленной цели необходимо решить ряд задач:

1) Понятие оптимальности по Парето;

2)Отношение доминирования по Парето. Парето-оптимальность;

3) Изучить аналитические методы построения множества Парето и тд.

Объектом данной курсовой работы является оптимальность решений по Парето, а предметом умение эффективно принимать решения по оптимальности Парето.

Ранее, при исследовании проблемы многокритериальности часто все критерии, кроме одного, выбранного доминирующим, принимались в качестве ограничений. Впервые проблема оптимизации векторного критерия была сформулирована экономистом Парето в 1896 г.

В задачах математического программирования с одним критерием нужно определить значение целевой функция, соответствующее, например, минимальным затратам или максимальной прибыли. Однако, немного подумав, мы практически в любой реальной ситуации обнаружим несколько целей, противоречащих друг другу.

Приведем пример того, насколько широк диапазон проблем, которые могут быть адекватно сформулированы как многокритериальные, и какие характеристики следует использовать в качестве критериев.

1. Оптимальность по Парето

1.1 Отношение доминирования по Парето. Парето-оптимальность

Для облегчения результатов полезно всё время проводить аналогию с однокритериальным (классическим) случаем. Пусть имеется область D и задана функция f – целевая функция (критерий). Задача оптимизации имеет вид:^[1]

min f(X)

X∈D

Точка X₁∈D называется оптимальной (недоминируемой, неулучшаемой), если не существует точки X₂∈D, для которой f(X₁)>f(X₂) (целевая функция минимизируется). Аналогично в МЗО можно исключить из области D точки, которые заведомо не могут оказаться наилучшими.

Очевидно, что в обобщённом смысле определение оптимальности можно трактовать как описание (выделение) в подмножестве D некоторого нового подмножества D₀, т.е. некоторое сужение D до D₀ ⊂D. В зависимости от характера описания, подмножество D₀ может оказаться пустым, состоять из одного элемента, содержать более одного элемента. Описание D₀ можно проводить либо только с помощью критериев Fi, либо использовать дополнительные условия. Здесь мы рассмотрим направление, которое связано с определением оптимальности по Парето.

Как было сказано раньше для всякого решения X∈D набор его оценок по всем критериям, т.е. набор (F₁(X), F₂(X), . . .,Fm(X)), есть векторная оценка решения X. Векторная оценка X содержит полную информацию о ценности (полезности) этого решения ЛПР и сравнение двух решений сравнение их оценок. Пусть в требуется получить значения каждого критерия (минимизировать критерии) Fi(X).

: Пусть имеются решения X₁ и X₂. Говорят, решение X₁ лучше (, эффективнее, доминирует) X₂, если F_i(X₁)<=(X₂) для всех i=1,m, и бы для j — го критерия строгое неравенство (X₁)<F_i(X₂). или

: Решение X₂ называется , если существует X₁, не хуже X₂, т.е. для любой функции Fi, I=1, 2, …, m,

(X₂)≤Fi(X₁) при функции Fi,

(X₂)≥Fi(X₁) при Fi.

В случае при переходе X₂ к X₁ ничего не проиграно ни одному из критериев, но в j — го частного точно будет выигрыш. Говорят, решение X₁ лучше () решения X₂.

Определение: X₁∈D называется эффективной ( по Парето), не существует X₂∈D такой, что (X₂) ≤Fi(X₁), i=1, . . ., m, F(X₂)≠F(X₁), или:

: Если решение доминируемо никаким решением, то называется недоминируемым оптимальным в смысле .^[2]

Очевидно, тогда в множества D нет сохранять решение X₂, вытесняется (или, говорят, “доминируется”) X₁. Ладно, выбросим, X₂ как неконкурентоспособное и к сравнению других по всем . В результате такой отбрасывания заведомо , невыгодных решений D обычно сильно : в нём сохраняются так называемые (иначе “паретовские”) , характерные тем, ни для из них существует доминирующего . Множество таких и называется множеством оптимальных по . Множество точек по Парето между точками , полученных при задачи математического для каждого критерия. В литературе точек оптимальных Парето, как , обозначают буквой P (P⊂D).

.^[3] Множество векторных , соответствующих множеству точек, называют компромиссов (переговорным ) или множеством в области критериев. обозначать Y_P ( ⊆Y_D).

Опр. векторных оценок, множеству неэффективных (доминируемых решений), областью согласия .

В области Y_c противоречия между критериями оптимальности, т.к. точка X∈D может изменена таким , что будет улучшены все критерии.

Если критериев Y_D только из согласия Y_c, существует единственная X_opt∈D, в которой частные критерии между собой в смысле, что движении к точке все F_i(X) i=1, 2, . . ., m, улучшаются. Все критерии достигают в т. X_opt (см. . 1). Такую точку оптимальным решение и этом значения частных критериев в ней минимума.

. 1

Критерии F1 и F2 непротиворечивы

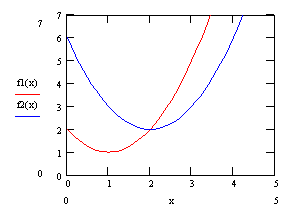
такая ситуация крайне редко. типичным является , когда частные являются противоречивыми и по каждому них достигается в точках. В этом уменьшение одного критерия приводит к других частных (рис. 2).

Рис. 2

F1 и F2 противоречивы на [1; 2]

Оптимальность по означает, что дальше улучшать одного критерия, ухудшая при хотя бы из остальных.^[4]

приём выделения решений на задачи с двумя F₁ и F₂ (оба требуется ). Множество D состоит 11 возможных решений. решению соответствуют значения показателей F₁ и F₂. имеются следующие оценки: F(X₁)=(2;4), F(X₂)=(3;5), F(X₃)=(3;3), F(X₄)=(5;2), F(X₅)=(4;3), F(X₆)=(1;3), F(X₇)=(2;3), F(X₈)=(3;2), F(X₉)=(2;2), F(X₁₀)=(3;1), F(X₁₁)=(2;1). Векторные исходов представим координатной плоскости ( оси абсцисс значения критерия F₁, а оси ординат – критерия F₂). Используем оптимальности по для выделения решений. Решение X₁ решением X₂, решение X₂ решений X₃, X₇, X₈, X₉, X₁₀ и X₁₁. Решение X₄ первому критерию решения X₅, а по наоборот, т.е. имеем решения, и т.д. После анализа у нас три решения X₂,X₄, X₅ по Парето.^[5]

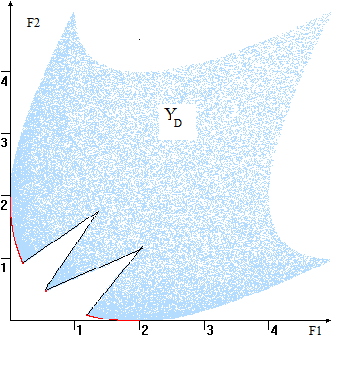
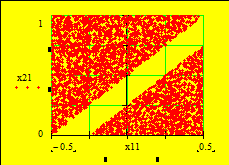
критериальное пространство нашей задачи. известно паре соответствует точка плоскости. Занумеруем соответственно номеру (рис 3). Из видно, что точки лежат правой верхней области возможных (Ауд. решить задачу, когда критерия нужно ).

Рис. 3

Множество

Когда из возможных решений эффективные, «переговоры» вестись уже в этого «эффективного» . На рис. 3 три решения X₂, X₄, X₅; них X₄ лучше критерию F₁, а решение X₂ критерию F₂. Дело , выбрать тот , который для предпочтителен и “приемлем” обоим критериям.

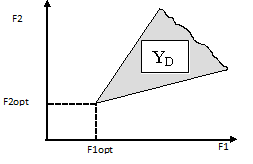
. Точка Y₁ выбирается в в том и только в случае, когда другая точка Y₂ Y_D имеет бы по координате значение чем Y₁ (критерии ).

Замечание. Для эффективных точек правило “уголка”. вида^[6] ∟ используется определения компромиссных в критериальном пространстве, критерии максимизируются, а ┐когда критерии .

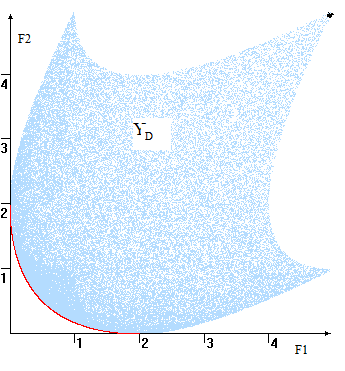
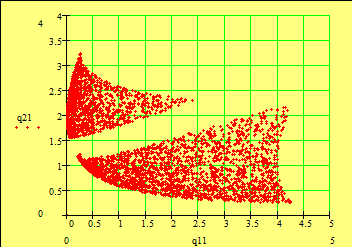
В случае, когда допустимых исходов непрерывным, их оценки «заполняют» область Y_D плоскости и получается «» вроде изображённой рис. 4. В этом множество Парето- оценок (красная ) представляет собой границы Y_D, говоря, её «-западную» границу». критерии максимизируются – «северо-восточную» области Y_D.

. 4

Пространство оценок и компромиссная кривая ( цвет)

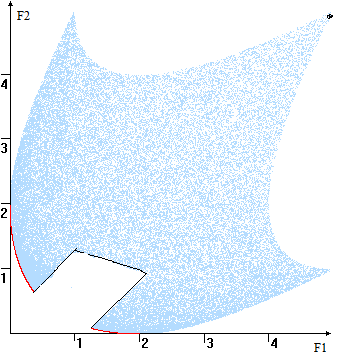
Замечание. В невыпуклой области Парето-оптимальная может иметь «экзотический» вид, , состоять из линий и/или . Для данного (критерии максимизируются) — правый пик.

. Экономисты так оптимальность по . Состояние называется по Парето, выполняется следующее : ничьё благосостояние может быть без ухудшения кого-либо .

Таким образом, оптимально-компромиссным будем понимать из эффективных , являющуюся предпочтительней с зрения ЛПР. векторной оптимизации позволяет однозначно на вопрос, ли оптимальное . Положительный ответ этот вопрос от качественной о важности частных , которая имеется у .

1.2 Аналитические методы множества Парето

кривая:^[7]

Особый для практики — m=2. В случае множество точек представляет одномерное многообразие плоскости и допускает графическое представление.

. ^[8]Множество паретовских в двухмерном пространстве называют компромиссной .

Она может из несвязных и содержать изолированные (см. рис. 5). кривая (КК) монотонно убывает в смысле. Пусть Y₁ и Y₂ точки, принадлежащие . Обозначим их Y₁(y1,y2) и Y₂(y3,y4), если y1<y3, то y2>y4. образом, КК содержит ни , ни вертикальных и её уравнение быть представлено в F₂=u(F₁) и F₁=v(F₂).

Рис. 5

Примеры (компромиссная кривая красным цветом)

1.3 Примеры компромиссных кривых

подход. Если F₁(X) и F₂(X) дифференцируемы, то попытаться найти место точек поверхностей уровня F₁(X)=b1 и F₂(X)=b2. В точках gradF₁=-λ₂, 0≤ λ< ∞.

Последнее векторное равносильно n скалярным уравнениям которые кривую в пространстве x₁=ϕ₁(λ), …, x_n=ϕ_n(λ). Если этой кривой, котором λ≥0 принадлежит D, то он и множеству P (P — множество ). Участок КК в случае определяется уравнениями:^[9]

F₁=F₁(ϕ₁(λ), …, ϕ_n(λ)),

F₂=F₁(ϕ₁(λ), …, ϕ_n(λ)), λ≥0.

Пример 1. В D={-1≤ x₁ ≤ 1, -1≤ x₂ ≤ 1} заданы два

которые желательно .

1. Находим минимумы F₁ и F₂ . Абсолютные минимумы в точках (0,0) и (-1,1) и принадлежат D.

2. Находим частные

составляем систему :

4x₁=-λ (x₁+1)

x₂=-λ (x₂-1).

Отсюда получаем уравнение кривой в параметров

В данном можно получить этой кривой в прямоугольных координатах. этого решаем уравнения относительно λ. Получим

Приравнивая части и разрешая x₂, получим уравнение кривой P: .

Параметрическое КК будет следующий вид

F₁(λ)=

F₂(λ)=.

КК: F₁ возрастает 0 до 5, а F₂ убывает 2 до 0.

Построим паретовских кривых в D и пространстве критериев (. 6 и 7).^[10]

Рис. 6 Область D и P Рис. 7 Компромиссная

Пример 2. В области D={-0.5 ≤ x₁ ≤ 0.5, 0 ≤ x₂ ≤ 1} два критерия

нужно минимизировать с функциональных ограничений ⎥x₂-x₁-0.375⎥ ≥ 0.125.

а) сначала случай функциональных ограничений

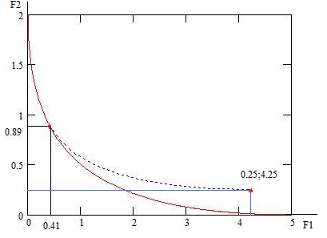
1. минимумы функций^[11] F₁ и F₂. минимумы находятся в X_1opt=(0,0) и X_2opt=(-1,1) и первая точка D, а вторая нет. условный минимум функции F₂: X_2услов=(-0.5, 1); находим F2(-0.5,1)=0.25, F1(-0.5,1)=4.25.

2. Находим частные

составляем систему

2x₁=-λ (x₁+1),

8x₂=-λ (x₂-1).

Отсюда получаем уравнение кривой в параметров

В данном можно получить этой кривой в прямоугольных координатах. этого решаем уравнения относительно λ. Получим:

Приравнивая части и разрешая x₂, получим уравнение кривой P: . Найдём пересечения кривой с x₁=-0.5. Xп=(-0.5; 0.2). Это случаю, когда λ от 0 до 1 (0≤ λ≤1).^[12]

уравнение КК иметь следующий (когда точки X_1opt=(0,0) и X_2opt=(-1,1) области D)

F₁(λ)=

F₂(λ)=.

Закономерность : F₁ возрастает от 0 4.25, а F₂ убывает от 2 0.

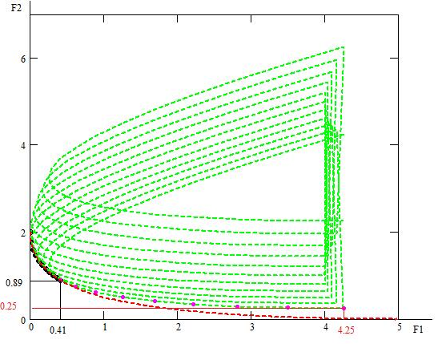
Построим графики кривых в области D и критериев (рис. 8 и 9).

. 8 Область D и множество P . 9 Компромиссная кривая

Xп

. 10

Пространство оценок и кривая

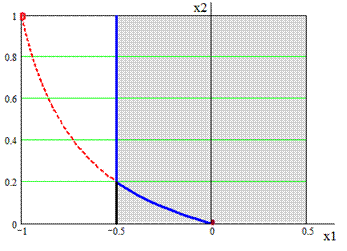
б) введём ограничения. Область D в случае будет вид (рис. 11). условный минимум функции F₁ и F₂ . Они в точках X_1opt=(0,0) и X_2opt=(-0.5, 1). Как из полученных точки минимумов изменились.^[13]

Рис. 11 D Рис. 12 Пространство

Из рассмотренного видно, что множества P в аналитическом является сложной . Поэтому в настоящее широко используются методы построения оптимальных по (см. раздел » методы получения Парето»).

1.4 Способы Парето-оптимального

Выделение множества МЗО часто является удовлетворительным . Это связано с , что при большом исходном вариантов множество оказывается недопустимо для того, ЛПР было в состоянии осуществить самостоятельно. Таким , выделение множества можно рассматривать как предварительный оптимизации, и налицо дальнейшего сокращения множества.

Для одной оптимальной из множества решений в каждой многокритериальной задаче использовать дополнительную о цели операции, т.е. информацию, которая задании векторного осталась неформализованной и неиспользованной.^[14]

Наиболее и последовательным представляется построения бинарного предпочтения, более , чем отношение , позволяющего сузить выбираемых вариантов приемлемых с точки ЛПР размеров. , для этого некоторая дополнительная , которую придётся от ЛПР. может быть о критериях, о самих вариантах и т.п. Задача, перед создателями , заключается в том, с помощью этой обосновать свои по сужению и гарантировать ЛПР того, чтобы один из , представляющих для интерес, не потерян в процессе .

Необходимо отметить, необоснованность сужения Парето является недостатком многих многокритериальной оптимизации.

образом, общая исследования задач решения на математического моделирования МЗО может реализована в рамках из следующих .

Первый подход. заданной многокритериальной оптимизации находится её Парето- решений, а выбор оптимального варианта множества Парето- предоставляется ЛПР.

подход. Как было сказано , производится сужение Парето-оптимальных (в идеале – до элемента) с помощью формализованных процедур, облегчает окончательный для ЛПР. , что такое может быть только при дополнительной информации о или свойствах решения.

Рассмотрим простейшие способы Парето-оптимального , акцентируя при внимание на дополнительной информации. , что задана задача оптимизации.

верхних границ . Дополнительная информация оптимальном исходе ∈D в этом случае вид:^[15]

(1)

Число рассматривается здесь верхняя граница i – му критерию.

, что указание границ по не может «извлечено» из модели задачи решения; набор (C₁, C₂, , C_m) представляет дополнительную информацию, от ЛПР.

. Выбор места :

Предположим, что предстоит выбрать работы из вариантов, представленных в .1. В качестве основных взяты: зарплата З, отпуска Д, время на работу В. смысла задачи , что критерии З и Д максимизировать, а критерий В – . Какой вариант оптимальным?

Таблица 1

Варианты	Критерий
Зарплата, (руб.)	Длительность отпуска, (дни)	Время поездки, (мин)
1	900	20	60
2	500	30	20
3	700	36	40
4	800	40	50
5	400	60	15
6	600	30	10
7	900	35	60
8	600	24	10
9	650	35	40

. Выделим вначале -оптимальные варианты. доминируемые по варианты {1, 2, 8, 9}, получаем -оптимальное множество {3, 4, 5, 6, 7}. отсутствии информации относительной важности критериев, а также о -либо дополнительных оптимального решения сужение Парето- множества произвести . Тогда формальный заканчивается указанием -оптимального множества и выбор оптимального производится ЛПР этих пяти на основе -то дополнительных .^[16]

Рассмотрим теперь подход, который к сужению Парето- множества на дополнительной информации, от ЛПР.

а) нижних границ . Наложим, например, ограничения на решение:

зарплата — менее 600 рублей;

отпуска — не 30 дней;

время — не более 40 .

Варианты, удовлетворяющие дополнительным ограничения: {3, 6, 9}; них оптимальными Парето являются 3 и 6. Остаётся сделать выбор между 3 и 6.

б) Субоптимизация. Пусть в выделенного (главного, ) критерия выступает зарплата; ограничения отпуска — не 30 дней, время — не более 40 . Отбросим варианты, не удовлетворяют ограничениям; остаются : {2, 3, 5, 6, 9}. Из них зарплату имеет 3. Этот вариант и оптимальным.^[17]

в) Лексикографическая . Упорядочим критерии относительной важности. , следующим образом: (т.е. критерий — зарплата, за ним важности время , наименее важный длительность отпуска). значение по З имеют варианты 1 и 7. сравниваем эти по второму важности критерию В. как время для этих одинакова, переходим к критерию Д; по длительность отпуска является вариант 7, и является здесь .

2. Численные методы множеств Парето

используют следующий . Во множестве D некоторая сетка, , координаты которой с помощью датчика чисел, распределённых равномерному закону. вычисляют значения критерия F в точках сетки, после за конечное сравнений, используя выбора по , строится множество на указанной , являющееся при N приближением множества относительно D (N – число сетки).

В рассмотренных моделях оптимизации выбора наилучшего (оптимального плана) при помощи максимизации скалярной , которая таким отражает степень целей объекта и часто называется функцией.^[18]

Однако такой целевой для реального объекта представляет , как правило, трудную задачу. этого связаны с характером целей , влиянием не экономических, но и факторов, сложностью полезности конечных хозяйственной деятельности и т.п. некая синтезированная цель производственного часто может выражена лишь в форме, но не поддается при помощи выраженной скалярной функции. В связи с оказывается перспективным , что объект перед собой достижения не общей цели, имеет в виду целей, каждой которой отвечает целевая функция. подход позволяет задачу выбора решения как многокритериальной оптимизации множестве Z допустимых интенсивностей технологических .

Пусть f _l ( z ) ( l = 1, …, L ) целевые , соответствующие системе L производственного объекта, на множестве Z . этом большему f _l отвечает более степень достижения l — цели. Можно , что требуется решение задачи оптимизации.

В данной векторная целевая f ( z ) выступает в виде между различными и позволяет условно некоторую, вообще , некорректную математическую , в которой требуется план, который бы точкой максимума для нескольких различных функций. Для того, чтобы хотя бы частично устранить эту неправильность, используются некоторые примирительные определения решений многокритериальной задачи.

Вообще говоря, оптимум Парето не является единственным. Совокупность всех таких оптимумов образует множество Парето, которое может иметь сложную структуру. Чаще всего представление о множестве Парето дается при помощи графического изображения в пространстве частных целевых функций (критериев).

Проблема описания множества Парето в конкретной задаче многокритериальной оптимизации оказывается обычно очень сложной и решается путем последовательного решения серии вспомогательных однокритериальных задач. При этом используется, в частности, тот факт, что оптимальный план всякой задачи вида является оптимумом Парето. Следовательно, изменяя коэффициенты, можно построить некоторый набор точек множества Парето.^[19]

Заключение

Процедура решения многокритериальной задачи методом последовательных уступок заключается в том, что все частные критерии располагают и нумеруют в порядке их относительной важности; максимизируют первый, наиболее важный критерий; затем назначают величину допустимого снижения значения этого критерия и максимизируют второй по важности частный критерий при условии, что значение первого критерия не должно отличаться от максимального более чем на величину установленного снижения (уступки); снова назначают величину уступки, но уже по второму критерию и находят максимум третьего по важности критерия при условии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше чем на величины соответствующих уступок; далее подобным, же образом поочередно используются все остальные частные критерии; оптимальной обычно считают любую стратегию, которая получена при решении задачи отыскания условного максимума последнего по важности критерия.

Таким образом, при использовании метода последовательных уступок многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин уступок. Величины уступок характеризуют отклонение приоритета одних частных критериев перед другими от лексикографического: чем уступки меньше, тем приоритет жестче.

Порядок решения детерминированных многокритериальных задач методом последовательных уступок:

При решении многокритериальной задачи методом последовательных уступок сначала производится качественный анализ относительной важности частных критериев; на основании такого анализа критерии располагаются и нумеруются в порядке убывания важности, так что главным является критерий , менее важен , затем следуют остальные частные критерии . Максимизируется первый по важности критерий и определяется его наибольшее значение.

Затем назначается величина «допустимого» снижения (уступки) критерия и ищется наибольшее значение второго критерия при условии, что значение первого критерия должно быть не меньше, чем .

Снова назначается величина уступки , но уже по второму критерию, которая вместе с первой используется при нахождении условного максимума третьего критерия, и т.д. Наконец, максимизируется последний по важности критерий при условии, что значение каждого критерия из предыдущих должно быть не меньше соответствующей величины; получаемые в итоге стратегии считаются оптимальными.

Список используемых источников

1. Веснин, В.Р. Менеджмент: Учеб.- 4-е изд., перераб. и доп.- М.: ТК Велби, 2016. — 342 с.

2. Герчикова , И.Н. Процесс принятия и реализации управленческих решений/ И.Н. Герчикова //Менеджмент в России и за рубежом, 2016. № 12. — 130 с.

3. Гончаров, В. И. Менеджмент: учебное пособие / В. И. Гончаров. — Минск : Современная школа, 2015.- 255 с.

4. Дробышев, А.В . Методы принятия решений. Методы Дельфи и ЭЛЕКТРА. — Методические указания к лабораторной работе по курсу «Системы поддержки принятий решений». — МГИЭМ. Сост.: И.Е.Сафонова,., К.Ю.Мишин, С.В.Цыганов: М., МГИЭМ, 2015. — 26 с.

5. Евланов, А. Г. Теория и практика принятия решений. — М.: Экономика, 2015. — 212 с.

6. Коротков, Э. М. Менеджмент : учебник для бакалавров / Э. М. Коротков. Москва :Юрайт, 2016.- 85 с.

7. Кривко, О.Б. Информационные технологии. М.: СОМИНТЭК. 2015. — 179 с.

8. Лафта, Дж. К. Эффективность менеджмента организации. — М.: Русская деловая литература, 2016. — 320 с.

9. Макаров, С.Ф. Менеджер за работой. — М.: ФИНПРЕСС, 2016. — 155 с.

10. Мескон , М. Основы менеджмента: Учебное пособие / М. Мескон, М. Альберт, Ф. Хедоури; М., 2016. — 387 с.

11. Панкрухина , А.П.Теория управления: учебник / [Ю. П. Алексеев и др.]; под общей редакцией: А. Л. Гапоненко, А. П. Панкрухина. — Москва: Издательство РАГС, 2015.- 213 с.

12. Пирожков, В.А. О реализации процессного подхода к управлению в виде системы поддержки принятия решений «Управление деятельностью организации» [Текст] / В.А. Пирожков // Вестник Тамбовского ун-та. Сер.: Гуманитарные науки. — 2015. — Вып. 11. — 489 с.

13. Полушкин, О.А. Стратегический менеджмент: конспект лекций. — М.: ЭКСМО, 2016. — 138 с.

14. Ромащенко, В.Н. Принятие решений: ситуации и советы. — Киев, 2015. — 154 с.

15. Румянцева З.П. Менеджмент организации: учебное пособие. — М.: ИНФРА-М, 2015. — 432 с.

16. Сараев, А. Д., Щербина О. А. Системный анализ и современные информационные технологии //Труды Крымской Академии наук.- Симферополь: СОНАТ, 2016.- 136 с.

17. Терелянский, П.В. Системы поддержки принятия решений. Опыт проектирования : монография / П.В. Терелянский ; ВолгГТУ.- Волгоград, 2015. -127 с.

18. Черняховская Л.Р. Поддержка принятия решений при стратегическом управлении предприятием на основе инженерий знаний / Л. Р. Черняховская и др. Уфа: АН РБ, Гилем, 2016. — 128 с.

1. Веснин, В.Р. Менеджмент: Учеб.- 4-е изд., перераб. и доп.- М.: ТК Велби, 2016. — 342 ↑

2. Герчикова , И.Н. Процесс принятия и реализации управленческих решений/ И.Н. Герчикова //Менеджмент в России и за рубежом, 2016. № 12. — 130 с. ↑

3. Гончаров, В. И. Менеджмент: учебное пособие / В. И. Гончаров. — Минск : Современная школа, 2015.- 255 с. ↑

4. Коротков, Э. М. Менеджмент : учебник для бакалавров / Э. М. Коротков. Москва :Юрайт, 2016.- 85 с. ↑

5. Евланов, А. Г. Теория и практика принятия решений. — М.: Экономика, 2015. — 212 с. ↑

6. Дробышев, А.В . Методы принятия решений. Методы Дельфи и ЭЛЕКТРА. — Методические указания к лабораторной работе по курсу «Системы поддержки принятий решений». — МГИЭМ. Сост.: И.Е.Сафонова,., К.Ю.Мишин, С.В.Цыганов: М., МГИЭМ, 2015. — 26 с. ↑

7. Кривко, О.Б. Информационные технологии. М.: СОМИНТЭК. 2015. — 179 с. ↑

8. Лафта, Дж. К. Эффективность менеджмента организации. — М.: Русская деловая литература, 2016. — 320 с. ↑

9. Макаров, С.Ф. Менеджер за работой. — М.: ФИНПРЕСС, 2016. — 155 с. ↑

10. Мескон , М. Основы менеджмента: Учебное пособие / М. Мескон, М. Альберт, Ф. Хедоури; М., 2016. — 387 с. ↑

11. Черняховская Л.Р. Поддержка принятия решений при стратегическом управлении предприятием на основе инженерий знаний / Л. Р. Черняховская и др. Уфа: АН РБ, Гилем, 2016. — 128 с. ↑

12. Панкрухина , А.П.Теория управления: учебник / [Ю. П. Алексеев и др.]; под общей редакцией: А. Л. Гапоненко, А. П. Панкрухина. — Москва: Издательство РАГС, 2015.- 213 с. ↑

13. Пирожков, В.А. О реализации процессного подхода к управлению в виде системы поддержки принятия решений «Управление деятельностью организации» [Текст] / В.А. Пирожков // Вестник Тамбовского ун-та. Сер.: Гуманитарные науки. — 2015. — Вып. 11. — 489 с. ↑

14. Полушкин, О.А. Стратегический менеджмент: конспект лекций. — М.: ЭКСМО, 2016. — 138 с. ↑

15. Полушкин, О.А. Стратегический менеджмент: конспект лекций. — М.: ЭКСМО, 2016. — 138 с. ↑

16. Ромащенко, В.Н. Принятие решений: ситуации и советы. — Киев, 2015. — 154 с. ↑

17. Терелянский, П.В. Системы поддержки принятия решений. Опыт проектирования : монография / П.В. Терелянский ; ВолгГТУ.- Волгоград, 2015. -127 с. ↑

18. Румянцева З.П. Менеджмент организации: учебное пособие. — М.: ИНФРА-М, 2015. — 432 с. ↑

19. Сараев, А. Д., Щербина О. А. Системный анализ и современные информационные технологии //Труды Крымской Академии наук.- Симферополь: СОНАТ, 2016.- 136 с. ↑

По этой ссылке вы найдёте полный курс лекций по математике:

Содержательные представления об устойчивости, выгодности и справедливости многообразны. Выше мы рассматривали проявление устойчивости через равновесие. Существует и иной вариант устойчивости ситуации, в большей степени, чем равновесность, отражающий черты ее выгодности. Это оптимальность по Парето. 5.1. Множество Парето Рассмотрим на плоскости (U, V) множество ft (рис.8).

Каждая его точка обладает одним из следующих свойств: либо все точки, ближайшие к ней, принадлежат множеству ft (такая точка называется внутренней точкой множества ft), либо сколь угодно близко от нее расположены как точки множества ft, так и точки, множеству ft не принадлежащие (такие точки называются граничными точками множества ft).

Граничная точка может как принадлежать множеству ft, так и не принадлежать. Здесь мы будем рассматривать только такие множества, которым принадлежат все точки границы. Множество всех граничных точек множества называется его границей. Обозначение: 0ft. Пусть М — произвольная точка множества ft, внутренняя или граничная, и (U, V)— ее координаты. Поставим следующий вопрос: можно ли, оставаясь во множестве ft, переместиться източки М в близкую точку так, чтобы при этом увеличились обе ее координаты. Если М — внутренняя точка, то это бесспорно возможно.

Если же М — граничная точка, то такое возможно не всегда (рис. 9). Из точек М, М2, Л#з это сделать можно, но уже из точек вертикального отрезка АВ можно переместиться, увеличивая лишь координату V (координата U при этом остается неизменной). Перемещая точку горизонтального отрезка PQ вправо, мы увеличиваем координату U (при этом координата V сохраняет свое значение). Что же касается дуги BQy то перемещение вдоль нее способно увеличить лишь одну из координат при одновременном уменьшении другой.

Тем самым, точки множества ft можно разбить на три класса: в первый класс относятся точки, которые, оставаясь во множестве ft, можно сдвинуть так, чтобы одновременно увеличились обе координаты (в этот класс попадают все внутренние точки множества ft и часть его граничных точек), второй класс образуют точки, перемещением которых по множеству П можно увеличить только одну из координат при сохранении значения второй (вертикальный отрезок АВ и горизонтальный отрезок PQ на границе множества ft), в третий класс попадут точки, перемещение которых по множеству Q способно лишь уменьшить либо одну из координат, либо обе (дуга BQ границы дП) (рис. 10).

Множество точек третьего класса называется множествам Парето, или границей Парето данного множества Q (выделено на рис. 10). 5.2. Метод идеальной точки Пусть на плоскости (х, у) задано множество и (рис. 11) и в каждой точке этого множества определены две непрерывные функции Рассмотрим следующую задачу. Во множестве и) найти точку у,), в которой Обычно это записывается так Сразу же отметим, что в общем случае поставленная задача решения не имеет.

В самом деле, нарисуем на плоскости (С/, V) все точки, координаты которых вычисляются по формулам Из рис. 12 видно, что наибольшее значение U — Umax — и наибольше значение V — Vmax — достигаются в разных точках, а точка с координатами лежит вне множества Q. Тем самым, в исходной постановке задача, вообще говоря, неразрешима — удовлетворить обоим требованиями одновременно невозможно. И, следовательно, нужно искать какое-то компромиссное решение.

Опишем один из путей, использующий множество Парето. точка утопии идеальная точка . Сначала на плоскости (U, V) задается целевая точка, в качеств координат которой часто выбирается сочетание наилучших значений обоих критериев U и V. В данном случае это точка ((7тм, Vmax). Вследствие того, что обычно такая точка при заданных ограничениях не реализуется, ее называют тонкой утопии. Затем строится множество Парето и на нем ищется точка, ближайшая к точке утопии — идеальная точка (рис. 13). 5.3.

Оптимальность по Парето в биматричной игре Рассмотрим биматричную игру с 2 х 2-матрицами Пусть средние выифыши игроков А и В.

Ситуация (р», q.) в биматричной игре А и В наказывается оптимальной по Парето, если из того, что вытекают равенства Иными словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш одного из игроков, не уменьшив при этом выигрыш другого. Различие ситуации равновесия от ситуации, оптимальной по Парето, состоите следующем: в ситуации равновесия ни один из игроков, действуя в одиночку, не может увеличить своего собственного выигрыша; в ситуации, оптимальной по Парето, игроки, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого.

Обратившись к игре «Дилемма узников», покажем, как практически отыскиваются оптимальные по Парето ситуации. Напомним, что соответствующие платежные матрицы в этой игре имели следующий вид Тем самым, на единичном квадрате (рис. 14) возможных значений вероятностей р и д заданы две функции Точки с координатами (U, 7), вычисленными по приведенным формулам, на плоскости (U, V) заполняют четырехугольник с вершинами Граница Парето этого множества — ломаная NKL.

Возможно вам будут полезны данные страницы:

Каждый из игроков заинтересован в наибольшем значении своего среднего выигрыша Оптимальность по Парето Множество Метод идеальной точки Нетрудно заметить, что в данном случае Тем самым, точкой утопии в этой задаче является начальная точка 0(0, 0). Ближайшая к ней точка множества Парето — К(-1, -1) (рис. 16). Идеальная точка К(-1, -1) — точка с наибольшими выигрышами для каждого из игроков — оказывается лучше, чем равновесная точка М(-6, -6), и ей соответствуют чистые стратегии обоих игроков Несколько слов в заключение На анализе полученных результатов стоит остановиться чуть подробнее.

Из приведенных примеров видно, что числа С и D из соотношений (#*) на с. 273 могут быть как положительными, так и отрицательными. Они могут, в частности, даже обращаться в нуль. Рассмотрим однако наиболее интересный в приложениях случай, когда ни С ни D нулю не равны, Тогда, как нетрудно видеть, точка равновесия определяется парой Эти формулы являются весьма примечательными: в равновесной ситуации выбор игрока А полностью определяется элементами платежной матрицы игрока В, (и не зависит от элементов его собственной платежной матрицы), а выбор игрока В в равновесной ситуации полностью определяется элементами платежной матрицы игрока А, (и не зависит от элементов его собственной платежной матрицы).

Иными словами, равновесная ситуация обоих игроков определяется не столько стремлением увеличить собственный выигрыш, сколько желанием держать под контролем выигрыш другого игрока (минимизировать этот выигрыш). И если, например, заменить в биматричной игре матрицу выплат игроку А, а матрицу выплат игроку В оставить прежней, то игрок А никак не изменит своего «равновесного» поведения (просто не обратит внимания на эту замену), в то время как игрок В изменит свою стратегию на новую, равновесную. Оптимальность по Парето Множество Метод идеальной точки Таким образом, в биматричной (неантагонистичсской) игре мы вновь встречаемся с антагонизмом.

Правда, теперь это уже не антагонизм интересов (как это было в антагонистической, матричной игре), а антагонизм поведения. Отметим, что в биматричными играх (в отличие от матричных) при наличии нескольких ситуаций равновесия средний выигрыш игрока в разных равновесных ситуациях различен (напомним, что в матричной игре выигрыш игрока один и тот же вне зависимости от количества точек равновесия). Но если средние выигрыши разнятся, то какую равновесную ситуацию следует считать оптимальной?

Наконец, сше одно, не менее

интересное. Вспомним, с какими трудностями мы столкнулись, пытаясь перевести эмоциональные оценки результатов общения студент-преподаватель в количественные показатели. В целом сохраняя основные соотношения, эти количественные оценки могут, конечно, изменяться как от студента к студенту, так и от преподавателя к преподавателю.

Однако, если эти изменения будут не слишком значительными — элементы платежной матрицы пошевельнутся «слегка» — то слегка пошевелятся и зигзаги, не изменяя ни своей обшей формы, ни взаимного расположения, а, значит, число равновесных ситуаций не изменится. Впрочем, сказанное относится лишь к случае, когда множество ситуаций равновесия конечно и состоит из нечетного числа точек (одной или трех).

Как принято говорить в подобных случаях, это число устойчиво относительно малых шевелений. Конечно, в некоторых биматричных играх равновесные ситуации случаются и вчи-стых стратегиях (в последнем из разобранных примеров таких ситуаций даже две). И (в принципе это совсем нетрудно) можно дать определение ситуации равновесия в чистых стратегиях. Найти ее (если она, конечно, существует) — дело довольно простое. Но, как показывают приведенные примеры, во-первых, чистой ситуации равновесия может вовсе не быть, а, во-вторых, даже при ее наличии не исключено существование равновесных ситуаций в смешанных стратегиях.

И желая найти их все, неизбежно приходится обращаться к описанному выше подходу. Реальные конфликтные ситуации приводят к разным видам игр. Различны и способы их анализа и разрешения. Мы остановились лишь на трех видах игр — матричных, позиционных и бима-тричных. Сделанный выбор обусловлен тем, что уже здесь можно наглядно показать, какой смысл вкладывается в термин игра и чем именно занимается теория игр, а также познакомить с относительно несложным математическим инструментарии, опирающимся на ключевые понятия вероятности, матрицы и координаты и позволяющим разрешать простейшие из этих видов игр.

Вместе с тем, нам не хотелось бы, чтобы у читателя сложилось впечатление, что доступными анализу могут быть только игры, описанные выше. Существует обширный, содержательный и интересный, привлекающий неослабевающее внимание исследователей класс игр, в которых хотя бы один из игроков имеет бесконечное множество возможных стратегий — бесконечные игры.

В этом — заключительном — разделе мы приведем три примера бесконечных игр: непрерывной игры на единичном квадрате (непрерывными называются бесконечные игры, в которых функции выигрышей непрерывно зависят от стратегий, выбираемых игроками), дуэли (играми с выбором момента времени, или играми типа дуэли, называются игры, характеризующиеся моментом выбора хода и вероятностями получения выигрыша в зависимости от времени, прошедшего от начала игры до момента выбора) и дифференциальной игры поиска (в дифференциальных играх допускается делать ходы непрерывно и связывать поведение игроков условиями, описываемыми дифференциальными уравнениями).

При этом мы ограничимся, как и ранее, играми двух лиц и проведем лишь постановку задач (описание возможностей в поведении игроков и построение функций выигрышей), хотя для каждой из приводимых игр разработаны достаточно эффективные подходы к построению их решения. Борьба за рынки (игра на единичном квадрате) Одна из конкурирующих фирм (игрок А) пытается вытеснить другую фирму (ифока В) с одного из двух рынков сбыта. Предположим, что общая сумма средств, выделенная на это игроком А, равна 1. Типичной стратегией игрока А является разделение выделенной суммы на две части: х (0 ^ х ^ 1) для первого рынка и 1 — х для второго.

Подобным образом выглядят и стратегии игрока В: выделение им части у (0 ^ у ^ 1) своей суммы на первый рынок и 1 — у на второй. Будем считать, что если игрок А добился превосходства на одном из рынков (на другом превосходства автоматически добивается игрок В), то он вытесняет противника с этого рынка и получает выигрыш, пропорциональный избытку вложенных средств с коэффициентом, характеризующим важность рынка (этот коэффициент равен к| для первого рынка и кг для второго).

Тогда функция выигрыша Н(х, у) игрока А определяется формулой Ясно, что функция выигрыша игрока В равна -Я(ж, у Дуэль Два дуэлянта (игроки А и #) начинают сходиться в момент времени t = 0. У каждого пистолет заряжен одной пулей. Они встретятся в момент времени t = 1 (если только ни один из них не застрелит другого раньше). Каждый из дуэлянтов может выстрелить, когда пожелает. Если при этом одному из них удастся поразить противника, а самому остаться невредимым, то он становится победителем (его выигрыш равен 1) и дуэль тут же прекращается. Если оба промахнутся, дуэль закончится вничью (выигрыш каждого из игроков равен 0).

Если оба выстрелят одновременно и каждый поразит противника, то дуэль также считаете я окончившейся вничью. Если игрок А произведет выстрел в момент времени , то его выстрел будет успешным с вероятностью р{х). Подобным же образом, выстрел игрока В в момент времени будет успешным с вероятностью q(y). При условии игрок А выиграете вероятностью р{х), а проиграет с вероятностью Тем самым, его средний выигрыш при будет равен С другой стороны, если х> у, его средний выигрыш будет равен

При х = у средний выигрыш Оптимальность по Парето Множество Метод идеальной точки Таким образом, функция выигрыша Н(х, у) игрока А имеет вид и антагонистическая игра задана. В частности, если игроки стреляют без промаха, р(х) = q(y) = 1, Дифференциальная игра поиска Ищущий (игрок А) стремится обнаружить уклоняющегося (игрока В). Оба игрока перемещаются с постоянными скалярными скоростями (а и /? соответственно) по плоскости внутри некоторой поисковой области П. В любой момент времени каждый из игроков управляет своим перемещением, задавая направление вектора скорости.

Пусть (хл, уА) и (хв, у в) — координаты игроков. Тогда имеем dt Игра поиска заканчивается в тот момент, когда игроки сблизятся на расстояние I > О, иными словами, когда будет выполнено неравенство В случае успешного обнаружения выигрыш игрока А считается равным I. Построение решения в этой игре существенно зависит от характера и степени информированности игроков. Все, о чем говорилось в этой книге, — примеры бескоалиционных игр, когда любые соглашения, обмен информацией, побочные платежи, совместный выбор стратегий запрещены. Другой важный класс составляют кооперативные игры, в которых разрешены самые разнообразные формы сотрудничества.

Возможность соглашений между игроками оказывает существенное влияние на исход игры. Если допустить, например, в игре «Дилемма узников» совместный выбор стратегий, то исход игры может оказаться совсем иным. При наличии побочных платежей по-иному окончится и «Семейный спор». Вне поля наших рассмотрений остались игры с одним участником, а также игры с участием трех и более игроков; последние особенно интересны, но они и трудны. Задачи к разделу 1.

Найдите нижнюю цену игры, верхнюю цену игры, определите седловые точки, оптимальные чистые стратегии и цену игры (если они существуют): а) 2. Найдите решения следующих матричных игр: 3. Найдите точные и приближенные решения следующих матричных игр: а) 1-й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}. 2-й ход делает игрок В: не зная о выборе игрока А на 1-м ходе, он выбирает число у из множества двух чисел {1,2}. 3-й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, зная значение у, выбранное игроком В на 2-м ходе, но не помня собственного выбора х на 1-м ходе.

б) /-йход делает игрок А: он выбирает число х из множества двух чисел {1, 2}. 2-йход делает игрок В: зная выбор игрока А на 1-м ходе, он выбираетчисло у из множества двух чисел {1, 2}. 3-й ход делает игрок А: он выбираетчисло z из множества двух чисел {1, 2}, не зная значения у, выбранного игроком В на 2-м ходе, но помня собственный выбор х на 1-м ходе. в) 1-й ход производится случайно: игрок О выбирает число х, равное 1 с вероятностью 0,3 и равное 2 с вероятностью 0,7. 2-й ход делает игрок А:

он выбирает число у из множества двух чисел {1, 2}, зная результат случайного выбора на 1-м ходе. 3-й ход делает игрок В он выбирает число z из множества двух чисел {1,2}, зная выбор у игрока А на 2-м ходе, но не зная случайного выбора х на 1-м холе. 4. Дайте графическое предстаааение, приведите к нормальной форме и найдите точное решение позиционной игры со следующей функцией выигрышей W(iу, z): Найдите решение биматричной игры: Найдите ситуации равновесия в каждом из двух случаев: Ответы