Равные вектора
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
 |
| рис. 1 |
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Проверим равенство компонентов векторов
ax = bx = 1
ay = by => 8 = 2 n => n = 8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторов
a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Проверим равенство компонентов векторов
ax = bx = 1
ay = by = 2
az = bz => 4 = 2 n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти пару векторов
Найти пары элементов в векторе
У меня есть следующий вектор. V =
Я хочу найти все пары элементов. Всего у меня будет К (К-1) / 2 пары элементов.
Каким должен быть псевдокод этого алгоритма.
Спасибо dasblinkenlight за вашу помощь. Я написал код, он может помочь кому-то в будущем:
Решение
Вот общие мысли о том, как это сделать:
- Есть N кандидаты в первый член пары
- Когда участник k выбран первым членом пары, есть N-k Кандидаты на второго члена пары
- Вы можете генерировать все пары, используя два вложенными петли
- Вы можете доказать, что общее количество пар N*(N-1)/2 с использованием формула для суммы арифметической прогрессии с шагом 1 ,
Вот как вы можете сделать это с помощью двух циклов:
Примечание. Приведенный выше код использует математические обозначения для интервалов, где квадратные скобки обозначают включение соответствующего конца в интервал, а круглые скобки обозначают исключение соответствующего конца.
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = и b = . Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Как найти вектор коллинеарный вектору
Формула
Примеры нахождения коллинеарного вектора
Подставим координаты заданных векторов в это равенство и найдем значение $m$:
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac =1,5$$
А тогда значения неизвестных параметров $m$ и $n$ находим из равенств
$$frac =2 Rightarrow m=6$$ $$frac =2 Rightarrow n=frac =0,5$$
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Равные векторы
В различных школьных учебниках определение равных векторов даётся по-разному.
В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.
Два вектора называются равными, если они совмещаются параллельным переносом.
(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).
Например, изображенные на рисунке
Равенство векторов обозначают так:
(Свойства равных векторов)
1) Равные векторы сонаправлены и имеют равные длины.
2) Равные векторы имеют равные координаты.
3) От любой точки можно отложить вектор, равный данному, и притом только один.
1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.
2) Пусть дан вектор
с началом в точке A(x1; y1) и концом в точке B(x2; y2).
По определению равных векторов, вектор
равный данному, получен из
Если этот параллельный перенос задан формулами
Найдём координаты каждого из векторов:
То есть координаты равных векторов
Что и требовалось доказать.
Таким образом, координаты задают длину и направление вектора, но не фиксируют его.
3) Пусть даны вектор
и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор
При таком параллельном переносе вектор
переходит в вектор
По определению равных векторов,
Что и требовалось доказать.
На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).
Например,
отложенный от точки C, равен вектору
(Признаки равенства векторов)
1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.
2) Если у векторов соответствующие координаты равны, то векторы равны.
1) Пусть векторы
сонаправлены и имеют одинаковые длины.
Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор
переводит в вектор
По определению равных векторов,
Что и требовалось доказать.
2) Пусть векторы
Параллельный перенос, заданный формулами
переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы
А это означает, что
Что и требовалось доказать.
В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.
Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.
http://b4.cooksy.ru/articles/kak-nayti-paru-vektorov
Материал
урока.
На
прошлых занятиях мы ввели понятие вектора в пространстве.
Отрезок,
для которого указано, какой из его концов является началом, а какой — концом,
называется вектором. Любая точка пространства также является вектором, нулевым
вектором.
Мы
выяснили, что длина ненулевого вектора равна длине
отрезка AB. А длина нулевого
вектора равна 0.
Так
же дали определение коллинеарным векторам. Это векторы, которые лежат на
одной прямой или на параллельных прямых.
Если
коллинеарные векторы имеют одинаковое направление, то они являются сонаправленными.
Если же их направления противоположны, то векторы называют противоположно
направленными.
На
этом уроке мы будем говорить о равных векторах. Определение равных векторов в
пространстве звучит так же, как и определение равных векторов на плоскости.
Равными
называют сонаправленные векторы, длины которых равны.
Ну,
а противоположно направленные векторы, длины которых равны, называют противоположными.
Рассмотрим
пример.
На рисунке изображён куб ABCDA1B1C1D1.
Среди векторов, показанных на рисунке, найдём пары равных и противоположных
векторов.
Перед
нами куб, и стоит вспомнить, что это за фигура. Это многогранник, все грани
которого являются квадратами. Значит, все рёбра куба равны между собой.
Векторы
и
коллинеарны.
Ведь понятно, что ребра AA1
и DD1
параллельны, как противоположные стороны квадрата. Аналогично, параллельны
рёбра DD1
и CC1.
А значит, параллельны рёбра АА1 и CC1.
Так же по рисунку понятно, что данные векторы сонаправлены, а их длины по
условию равны. Тогда векторы и
равны.
Векторы
и
равны по длине,
но противоположно направлены. Значит, эти векторы являются противоположными.
Векторы
и
равны
по длине и сонаправлены, а значит, равны.
Векторы
и
равны
по длине и противоположно направлены, а значит, противоположны.
Также
противоположно направленными и равными по длине будут векторы и
. Они являются
противоположными.
Так
мы с вами выписали две пары равных векторов и три пары противоположных
векторов.
Задача.
правильный
тетраэдр.
,
,
и
середины рёбер
,
,
и
.
1.
Среди изображённых векторов указать пары равных векторов.
2.
Установить вид четырёхугольника .
Решение.
Равными
являются сонаправленные векторы, длины которых равны.
А
для того чтобы векторы были сонаправлены, они должны быть коллинеарны. То есть
должны лежать на параллельных прямых или на одной прямой.
Никакие
рёбра тетраэдра не являются параллельными. Поэтому на рёбрах будем искать
векторы, лежащие на одной прямой. Такими являются векторы и
, а также
и
. Точки P
и М являются серединами соответствующих рёбер. Значит, равны длины векторов и
, а также
и
.
Но
векторы и
противоположно
направлены, а вот векторы и
— сонаправлены.
Так
мы нашли одну пару равных векторов, и
.
Далее
рассмотрим треугольник ABD.
Точки М и N — середины сторон AB
и AD. Значит, МN
— средняя линия. И она параллельна стороне BD,
а также равна её половине.
В
треугольнике CBD отрезок PQ
является средней линией. Он параллелен стороне BD
и равен её половине.
Так
мы получаем, что отрезки МN
и PQ параллельны и равны. Значит, векторы
и
коллинеарны и,
очевидно, сонаправлены. И так как равны их длины, то можно сказать, что эти
векторы равны.
Аналогично,
в треугольнике ADC отрезок NP
является средней линией. Он параллелен стороне AC
и равен её половине.
В
треугольнике ABC отрезок MQ
также
является средней линией. Он параллелен стороне AC
и равен её половине.
Отсюда
получаем, что отрезки NP
и MQ параллельны и равны. А значит,
можем сделать вывод о равенстве векторов и
.
Так
мы с вами нашли три пары равных векторов.
Теперь
осталось определить вид четырёхугольника MNPQ.
Нами
уже установлено, что противоположные стороны этого четырёхугольника параллельны
и равны. А это говорит о том, что данный четырёхугольник является
параллелограммом.
Но
так как все рёбра данного тетраэдра равны, то равны и длины средних линий,
рассматриваемых ранее треугольников.
Получаем,
что MNPQ — параллелограм, все
стороны которого равны между собой. А значит, данный четырёхугольник является
ромбом.
Ответ.
1) ,
,
; 2)
ромб.
Далее
вспомним, что от любой точки плоскости можно отложить вектор равный данному,
и притом только один.
Это
утверждение верно и для любой точки пространства.
Действительно,
если рассмотреть некоторый вектор и
произвольную точку пространства М. Через точки начала и конца данного вектора,
а также через точку М можно провести плоскость.
В
полученной плоскости отложим от точки М вектор равный вектору
. Очевидно, он
искомый. А из построений понятно, что он будет единственным. Ведь первая
аксиома стереометрии говорит, что через 3 точки пространства можно провести
только 1 плоскость.
Говорят
«вектор отложен от
точки М».
Выполним
задание.
В
параллелепипеде ABCDA1B1C1D1
точки K и М — середины сторон A1D1
и B1C1
соответственно. Стоит напомнить, что все грани параллелепипеда являются
параллелограммами, а их противоположные стороны равны. Значит, равны и их
половины.
Итак,
нам нужно назвать векторы, которые получатся, если от данной точки отложить
вектор, равный данному.
Первым
нам нужно назвать вектор, который получится, если от точки C
отложить вектор, равный вектору .
Нам
известно, что от точки пространства можно отложить только один вектор, равный
данному.
Вектор
отложен от
точки C и он равен вектору . Значит, вектор
искомый.
Далее
назовём вектор, который получится, если от точки D
отложить вектор, равный вектору .
Вектор
отложен от
точки D и равен вектору . Значит, он и
является искомым.
Так,
если от точки А1 отложить вектор, равный вектору , то мы получим
вектор .
Если
же от точки C1
отложить вектор, равный вектору , то мы получим
вектор .
И,
отложив от точки М вектор, равный вектору , мы получим
вектор .
Подведём
итоги урока.
На
этом уроке мы выяснили, что, так же как и на плоскости, в пространстве равными
называют сонаправленные векторы, длины которых равны.
Если
же векторы противоположно направлены и их длины равны, то такие векторы
называют противоположными.
Так
же мы отметили, что от любой точки пространства можно отложить вектор, равный
данному вектору, и притом только один.
Всем
этим знаниям мы нашли применение при решении задач.
Определение. Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Условие равенства векторов.Вектора равны, если их координаты равны.
Примеры задач на равенство векторов
Примеры плоских задач на равенство векторов
Пример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.
Решение:
a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Пример 2. При каком значении параметра n вектора a = {1; 8;} и b = {1; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by => 8 = 2n => n = 8/2 = 4
Ответ: при n = 4 вектора a и b равны.
Примеры пространственных задач на равенство векторов
Пример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.
Решение:
a = c — так как их координаты равны,
a ≠ b — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by = 2
az = bz => 4 = 2n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.
В данной публикации мы рассмотрим, какие векторы называются равными и как определить их равенство. Также разберем примеры задач по этой теме.
- Условие равенства векторов
- Примеры задач
Условие равенства векторов
Векторы a и b равны, если у них одинаковая длина, они лежат на одной или параллельных прямых, а также направлены одну и ту же сторону. То есть такие векторы коллинеарны, сонаправлены и равны по длине.
a = b, если a ↑↑ b и |a| = |b|.
Примечание: векторы равны, если равны их координаты.
Примеры задач
Задание 1
Какие из векторов являются равными: a = {6; 8}, b = {-2; 5} и c = {6; 8}.
Решение:
Из перечисленных векторов равны a и c, так как у них одинаковые координаты:
ax = cx = 6
ay = cy = 8.
Задание 2
Выясним, при каком значении n векторы a = {1; 18; 10} и b = {1; 3n; 10} равны.
Решение:
Сначала проверим равенство известных координат:
ax = bx = 1
az = bz = 10
Чтобы равенство было верным, нужно чтобы ay = by:
3n = 18, следовательно n = 6.
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие вектора
Иногда, к примеру, в физике, для характеристики некоторых величин необходимо не только их числовое значение, но и направление (скорость, ускорение, сила…). Такие величины называются векторными величинами или коротко векторами. Напомним, что величины, не требующие направления, называются скалярными величинами.
Для введения понятия геометрического вектора будем использовать понятие отрезка. Введем следующее определение.
Определение 1
Граничные точки отрезка — это концы отрезка.
Отрезок может иметь два направления. Для обозначения направления будем называть одну граничную точку отрезка началом, а другую концом. Направление будет указываться от начала отрезка к его концу.
Определение 2
Вектором или направленным отрезком называется отрезок, для которого указано, какая из граничных точек считается началом, а какая концом данного отрезка.
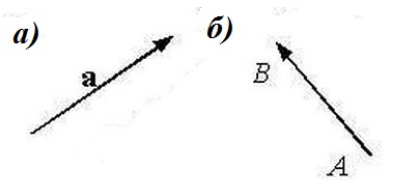
Обозначение: $overrightarrow{AB}$ — вектор $AB$ с началом в точке $A$ и концом в точке $B$.
Также вектор может обозначаться одной маленькой буквой: $overrightarrow{a}.$
Рисунок 1. Примеры векторов: а) вектор $overrightarrow{a}$; б) вектор $overrightarrow{AB}$.
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Нулевым вектором называется любая точка плоскости.
Обозначение: $overrightarrow{0}$.
Определение 4
Длиной или модулем вектора $overrightarrow{a}$ называется длина отрезка $a.$
Обозначение: $|overrightarrow{a}|$
«Векторы, понятие вектора, равенство векторов» 👇
Замечание 1
Отметим, что длина нулевого вектора равна нулю: $left|overrightarrow{0}right|=0$.
Равенство векторов
Для введения определения равных векторов для начала нужно ввести несколько других понятий.
Определение 5
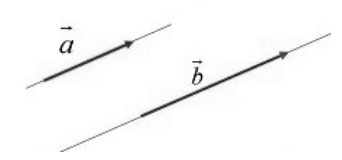
Ненулевые векторы называются коллинеарными, если они принадлежат одной прямой или расположены на параллельных прямых (рис.2).
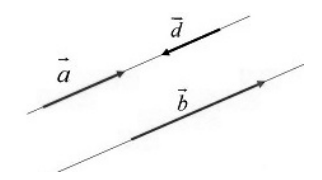
Рисунок 2. Коллинеарные векторы
Определение 6
Ненулевые векторы называются сонаправленными, если они:
-
Коллинеарны.
-
Направлены в одну и туже сторону (рис. 3).
Рисунок 3. Сонаправленные векторы
Обозначение: $overrightarrow{a}uparrow uparrow overrightarrow{b}$
Определение 7
Ненулевые векторы называются противоположно направленными, если они:
-
Коллинеарны.
-
Направлены в разные стороны (рис. 4).
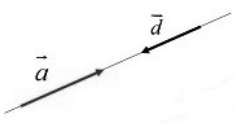
Рисунок 4. Противоположно направленные векторы
Обозначение: $overrightarrow{a}uparrow downarrow overrightarrow{d}$
Введем теперь непосредственно определение равных векторов.
Определение 8
Векторы называются равными, если:
-
Они являются сонаправленными;
-
Они имеют равные длины.
То есть, если $overrightarrow{a}uparrow uparrow overrightarrow{b}$ и $left|overrightarrow{a}right|=|overrightarrow{b}|$, то $overrightarrow{a}=overrightarrow{b}$ (рис. 5).
Рисунок 5. Равные векторы
Примеры задач на понятие вектора
Пример 1
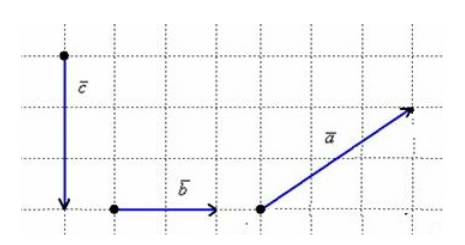
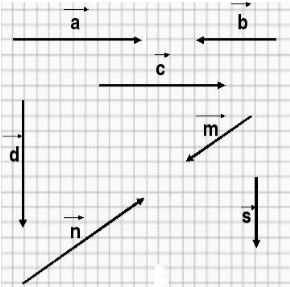
Найти длину векторов, если одна клетка имеет площадь $1 {см}^2$(рис. 6).
Рисунок 6.
Решение.
Так как клетка имеет площадь $1 {см}^2$, то очевидно, что
[left|overrightarrow{b}right|=2] [left|overrightarrow{c}right|=3]
Длину вектора $overrightarrow{a}$ найдем с помощью теоремы Пифагора. Получим:
[{|overrightarrow{a}|}^2=3^2+2^2] [{|overrightarrow{a}|}^2=9+4] [{|overrightarrow{a}|}^2=13] [left|overrightarrow{a}right|=sqrt{13}]
Ответ: $left|overrightarrow{a}right|=sqrt{13}$, $left|overrightarrow{b}right|=2$, $left|overrightarrow{c}right|=3$.
Пример 2
Найти равные векторы (рис 7).
Рисунок 7.
Решение.
Используя определение 8, видим, что $overrightarrow{a}uparrow uparrow overrightarrow{c}$ и $left|overrightarrow{a}right|=|overrightarrow{c}|$, следовательно, $overrightarrow{a}=overrightarrow{c}$
Ответ: $overrightarrow{a}=overrightarrow{c}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме