Как найти пары пропорциональные отрезки

Пропорциональные отрезки

Отрезки AB и CD пропорциональны отрезкам AB₁ и CD₁, если:

или

Отношением отрезков AB и CD называется отношение их длин, т.е. ( frac {AB}{CD}. )

Пример 1. На рисунке 1 заданы отрезки ( small AB, ; CD, ; A_1B_1,; C_1D_1. ) Определить, являются ли отрезки ( small AB ) и ( small CD ) пропорциональны отрезкам ( small A_1B_1 ) и ( small C_1D_1 ).

Решение. Запишем длины отрезков:

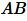
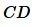
Отношение отрезков и равно:

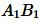
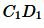
Отношение отрезков и равно:

Выполнено равенство

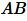
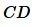
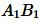
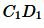
значит отрезки и пропорциональны отрезкам и .

Легко убедится, что выполяется также равенство (2) (это следует также из правила перекрестного умножения):

Пример 2. На рисунке 2 заданы отрезки ( small AB, ; CD, ; A_1B_1,; C_1D_1. ) Определить, являются ли отрезки ( small AB ) и ( small CD ) пропорциональны отрезкам ( small A_1B_1 ) и ( small C_1D_1 ).

Решение. Запишем длины отрезков:

Тогда

Следовательно

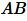
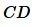
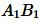
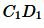
Следовательно отрезки и не пропорциональны отрезкам и .

Теорема Фалеса и теорема о пропорциональных отрезках

ТЕОРЕМА ФАЛЕСА:

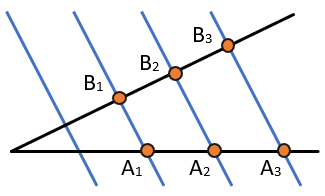
1. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

<>

Если (A_{1}B_{1} parallel A_{2}B_{2} parallel A_{3}B_{3}), (A_{1}A_{2} = A_{2}A_{3}), то (B_{1}B_{2} = B_{2}B_{3}).

2. Эта теорема применима также и к пересекающимся прямым:

Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекает равные отрезки и на другой прямой.

3. Из теоремы Фалеса следуют определения средней линии треугольника и средней линии трапеции.

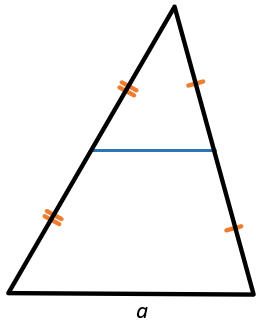
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

(a parallel m, m = frac{1}{2}a)

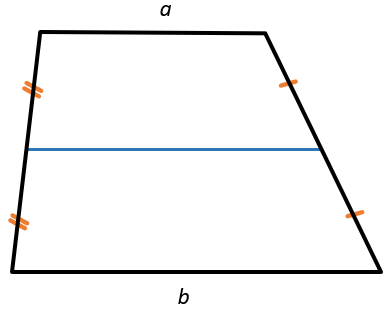
Средняя линия трапеции параллельна основаниям и равна их полусумме:

(m parallel a, b, m = frac{a + b}{2})

ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ:

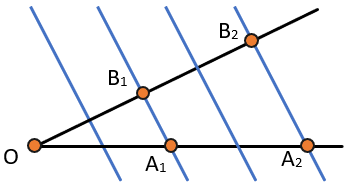
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Если (A_{1}B_{1} parallel A_{2}B_{2},) то (frac{OA_{1}}{OA_{2}} = frac{OB_{1}}{OB_{2}})

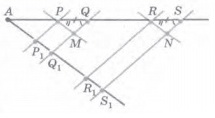
Теорема. Если на одной стороне угла отметить отрезки равной длины и провести несколько параллельных прямых через их концы, то эти прямые на другой стороне высекают также равные отрезки.

Доказательство. Пусть на одной стороне угла А отмерены отрезки PQ и RS, которые равны между собой. Через концы этих отрезков провели прямые, которые параллельны между собой и которые пересекают  вторую сторону угла А в точках Р₁, Q₁, R₁, S₁. Докажем, что отрезки Р₁Q₁ и R₁S₁ равны.

Через точки Р и R проведем прямые, параллельные другой стороне угла, которые пересекают прямые QQ₁ и SS_l в точках М и N соответственно.

Треугольники PQM и RSN равны, так как их стороны PQ и RS равны по условию, углы PQM и RSN равны как соответственные при параллельных QQ₁ и SS₁, пересеченных прямой AS, углы QPM и SRN равны как соответственные при параллельных РМ и RN, пересеченных прямой AS. Поэтому соответствующие стороны РМ и RN этих треугольников одинаковые.

Четырехугольники РР₁Q₁M и RR₁S₁N  —  параллелограммы. Поэтому отрезки P₁Q₁ и R₁S₁ равны соответственно отрезкам РМ и RN.

Поскольку отрезки РМ и RN равные, то равны и отрезки P₁Q₁ и R₁S₁.

Эта теорема называется теоремой Фалеса.

Фалес Милетский (около 625—547 до н. э.) — философ, математик и астроном, который, как считают, был первым греческим геометром.

Теорема. Если от вершины угла отложить последовательно равные друг другу отрезки на одной его стороне  и на другой стороне также равные друг другу отрезки, то прямые, проходящие через соответствующие концы отложенных отрезков, параллельны.

Доказательство. Пусть на одной стороне угла С от его вершины отмечены отрезки СМ и MN равной длины, на другой стороне — отрезки CP и PQ равной длины.

Докажем, что прямые MP и NQ параллельны. Через точку N проведем прямую, которая будет параллельна прямой MP. Пусть эта прямая пересекает сторону CP в точке Q₁. Тогда, по теореме Фалеса, PQ_l = СР. Но в соответствии с условием CP = PQ. Поэтому PQ_l = PQ, а это означает, что точки Q₁ и Q совпадают. Значит, прямая NQ_l совпадает с прямой NQ, и поэтому прямая NQ параллельна прямой MP.

Теорему Фалеса можно обобщить на так называемые пропорциональные отрезки.

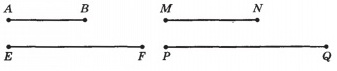
Пары отрезков (АВ, EF) и (MN, PQ) называют пропорциональными отрезками, если отношение отрезков одной пары равно отношению отрезков другой пары, т. е. AB/EF = MN/PQ.

Теорема. Если стороны угла пересечены тремя прямыми, которые друг другу параллельны , то отношение отрезков, которые образуются на одной из сторон угла, совпадает с отношением соответствующих отрезков, образованных на второй стороне угла.

Эта теорема позволяет утверждать, что если даны угол А и прямая р, то любая пара прямых, которые параллельны прямой р, отсекают на сторонах угла два отрезка, отношение длин которых постоянно и определяется только направлением прямой р.

Теорема. Если от вершины угла отложить последовательно на одной его стороне два отрезка, а на другой стороне два пропорциональных им отрезка, то прямые, проходящие через соответствующие концы отложенных отрезков, параллельны.

Теорема. Биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам.

Как разделить отрезок на n равных частей можно, обратившись к администратору Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра.. Также совершенно бесплатно мы расскажем вам как разделить отрезок в отношении m/n или как построить четвертый отрезок, пропорциональные первым трем данным.