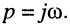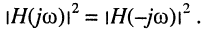Важнейшей
характеристикой линейной электрической
цепи является комплексная
передаточная функция H(jω).
При этом электрическую цепь удобно
изображать в виде четырехполюсника
(рис. 4.1), на входные зажимы (1 — 1’) которого
подается сигнал в виде напряжения с
комплексной амплитудой Uт1, или
тока с комплексной амплитудой Im1,
а реакция снимается с выходных зажимов
(2 — 2′) также в виде напряжения или тока
с комплексными амплитудами Um2, Im2. Комплексная
передаточная функция (КПФ) определяется
как отношение комплексной амплитуды
реакции цепи к комплексной амплитуде
входного воздействия.
В
зависимости от типов входного воздействия
и реакции цепи различают следующие виды
КПФ:
1. Комплексная
передаточная функция по напряжению
Комплексные
передаточные функции определяются на
частоте со сигнала воздействия и зависят
только от параметров цепи.
Как
всякую комплексную величину H(jω) можно
представить в показательной,
тригонометрической и алгебраической
форме:
есть
вещественная и мнимая
части комплексной
передаточной функции цепи.
Из
(4.5) —(4.8) нетрудно получить соотношения,
связывающие АЧХ и ФЧХ с вещественными
и мнимыми частями комплексной передаточной
функции
АЧХ
и ФЧХ являются наиболее фундаментальными
понятиями теории цепей и широко
используются на практике. Важность этих
характеристик для систем электрической
связи, радиовещания и телевидения
объясняется самой природой передачи
сигналов определенного спектрального
состава по каналам связи. Требования
к АЧХ и ФЧХ различных устройств являются
определяющими при проектировании
любой аппаратуры связи, так как от
степени их выполнения во многом зависит
качество передачи информации.
Пример. Определить
КПФ по напряжению Hu(jω),
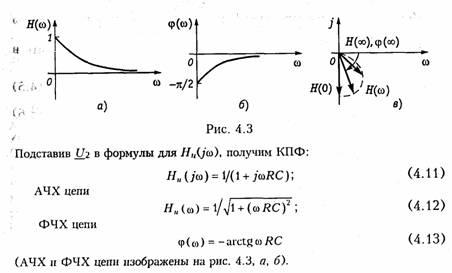
АЧХ и ФЧХ цепи, изображенной на рис. 4.2.
Согласно (4.1) запишем:
АЧХ
и ФЧХ цепи можно представить единым
графиком, если построить зависимость
КПФ H(jω)
от частоты со на комплексной плоскости.
При этом конец вектора H(jω)
опишет некоторую кривую, которая
называется годографом комплексной
передаточной функции (рис. 4.3, в).
В
ряде случаев частотные характеристики
цепи могут изменяться в очень широких
пределах, поэтому более удобно их
оценивать в логарифмическом масштабе.
С этой целью для оценки АЧХ вводят
понятие логарифмической
амплитудно-частотной характеристики (ЛАХ):
Оценивается
ЛАХ согласно (4.14) в децибелах (дБ). В
активных цепях К называют
еще логарифмическим
усилением. Для
пассивных цепей вместо коэффициента
усиления оперируютослаблением
цепи:
которое
также оценивается в децибелах.
Наряду
с передаточными функциями (4.1) —(4.4) в
ряде случаев (см. гл. 16, 17,18) находят
применение комплексные функции,
определяющиеся отношением комплексной
реакции к комплексному воздействию
на входных зажимах электрической цепи
(рис. 4.4)
Функции
вида (4.16) носят название комплексных
входных функций цепей.
3.2. Частотные характеристики последовательного колебательного контура
В
радиотехнике и электросвязи большое
значение имеет явление
резонанса. Резонансом называют
такое состояние электрической цепи,
состоящей из разнохарактерных реактивных
элементов, при котором фазовый сдвиг
между входным током и приложенным
напряжением равен нулю. Цепи, в которых
возникает явление резонанса,
называют колебательными
контурами,или резонансными
цепями.
Колебательные
контуры и явления резонанса находят
широкое применение в радиотехнике и
электросвязи. Резонансные цепи являются
составной частью многих радиотехнических
устройств: избирательные цепи в
радиоприемниках и усилителях,
частотно-зависимые элементы
автогенераторов, фильтров, корректоров,
других устройств. Для получения
высоких технико-экономических показателей
(избирательности, полосы пропускания,
коэффициента прямоугольности,
равномерности и т. д.) резонансные цепи
должны иметь достаточно сложную структуру
(многоконтурные связанные цепи, активные
резонансные системы и др.). Некоторые
из этих систем будут рассмотрены в гл.
15, 17. В настоящей главе изучим основные
особенности работы цепей в режиме
резонанса на примере простейших
колебательных контуров.
Простейший
колебательный контур содержит индуктивный
и емкостный элементы, соединенные
последовательно {последовательный
контур) или
параллельно (.параллельный
контур).В
последнее время широкое распространение
получили резонансные цепи на базе
операционных усилителей (ОУ). Различают
два типа резонансов: напряжений и
токов. В последовательном контуре
возникает резонанс
напряжений, а
в параллельном — резонанс
токов.
Частоту,
на которой наблюдается явление резонанса,
называют резонансной.
На
рис. 4.5 изображена схема последовательного
контура с реактивными элементами L и С и
резистивным сопротивлением R, характеризующим
потери в контуре. Приложим к контуру
гармоническое напряжение с
частотой ω. Комплексное входное
сопротивление контура на данной частоте
определяется согласно уравнению
На
резонансной частоте комплексное
сопротивление носит чисто активный
характер, т. е. Z = R, ток
совпадает по фазе с приложенным
напряжением и достигает максимального
значенияIо
= U/R. Реактивные
сопротивления контура на резонансной
частоте ω0 равны
друг другу:
Величина
ρ носит название характеристического
сопротивления контура.
Резонансные
свойства контура характеризуются добротностью
контура, которая
в общем случае определяется величиной
где Wp —
максимальные значения реактивной
энергии, запасенной в контуре при
резонансе; WT — активная
энергия, поглощаемая в контуре за
период Т. Величина,
обратная добротности, называется затуханием
контура и
обозначается d:
Величина Q безразмерна
и обычно колеблется для реальных контуров
от 10 до 100 и выше. Для выяснения физического
смысла параметра Q исследуем
энергетические соотношения в контуре
при резонансе. Положим, например, что
при резонансе ток в цепи Определим
согласно (1.10) и (1.13) сумму энергий
электрического и магнитного полей:
так
как уменьшение WL сопровождается
увеличением We и
наоборот. Таким образом,
происходит
периодический обмен энергией между
элементами I и
С без участия источника. Энергия
источника расходуется только на
покрытие тепловых потерь в элементе
активного сопротивления R; реактивная
мощность при резонансе не потребляется.
Активная
энергия, рассеиваемая в контуре за
период Т, равна
Таким
образом, добротность Q показывает,
во сколько раз резонансные напряжения
на реактивных элементах превышают
приложенное напряжение. Отсюда
следует и термин «резонанс напряжений».
Это свойство контура «усиливать»
приложенное напряжение резонансной
частоты широко используется на практике.
Величины
ρ, ωо, Q, d являются вторичными
параметрами контура
в отличие от величин R, L,
С называемых первичными.
Анализируя
характер уравнений напряжений и
токов в RLC-цепи,
фазовых сдвигов между ними при
гармоническом воздействии нетрудно
видеть, что они являются
частотно-зависимыми. Эта зависимость
вытекает непосредственно из зависимости
реактивных
элементов XL И ХС .ОТ
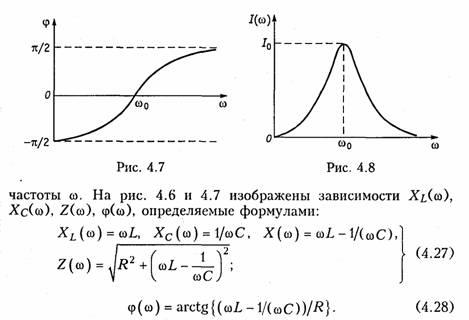
Из
представленных характеристик следует,
что при ω <ω0 цепь
имеет емкостный характер (Х<0; φ <0)И
ТОК опережает
по фазе приложенное напряжение при ω
>ω0 характер
цепи индуктивный (X >
0; φ > 0) и ток отстает по фазе от
приложенного напряжения; при со = соо
наступает резонанс напряжений (X = 0;
φ = 0) и ток совпадает по фазе с приложенным
напряжением. Полное сопротивление
цепи принимает при этом минимальное
значение Z = R.
Зависимость
действующего значения тока от частоты
можно найти из уравнения (4.18)*:
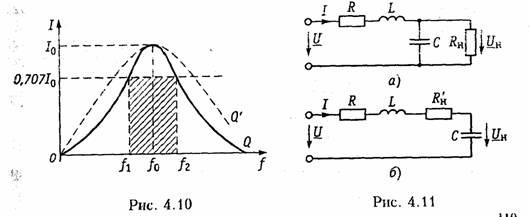
Зависимости I(ω), UL(ω), UC(ω) называются резонансными
характеристиками тока и напряжений. Анализ
зависимости I(ω)
показывает, что она достигает максимума
при резонансе ω =ω0
Выходное
напряжение обычно снимается с емкостного
или индуктивного элемента контура.
В соответствии с этим представляет
наибольший практический интерес КПФ
по напряжению относительно элементов
С и L:
Анализ
полученных зависимостей показывает,
что с увеличением добротности Q (уменьшением
затухания d) частоты
ωс и ωL сближаются
с резонансной частотой ωо.При
этом CCт и HLmвозрастают.
Степень
отклонения режима колебательного
контура от резонанса принято
оценивать абсолютной,
относительной и обобщенной
расстройками. Отклонение
от резонансного режима может происходить
в результате изменения частоты; задающего
генератора или
вариации параметров
контура.
Расстройки
определяются следующим образом:
абсолютная
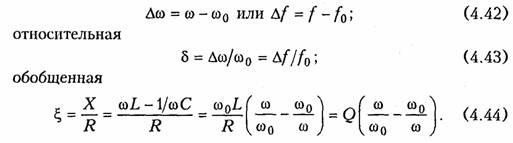
Наиболее
широко в теоретических исследованиях
применяется обобщенная расстройка ζ, так
как ее использование существенно
упрощает расчет. Например, модуль входной
проводимости можно записать через
обобщенную расстройку ζ, в форме
Важной
характеристикой колебательного контура
является полоса пропускания. В общем
случае абсолютной
полосой пропускания называют
диапазон частот в пределах которого
коэффициент передачи уменьшается в √2
раз по сравнению с максимальным*.
Абсолютная полоса пропускания равна
Уравнения
(4.50) могут быть положены в основу
экспериментального определения
добротности по резонансной кривой
тока I(ω).
Формула (4.50) показывает, что чем выше
добротность Q,
тем меньше полоса пропускания и наоборот.
Причем, поскольку с увеличением
потерь R добротность
контура падает, то подключение к
контуру сопротивления нагрузки или
источника с внутренним сопротивлением
приводит к расширению полосы пропускания.
Пример. Определить
полосу пропускания контура, нагруженного
на резистивное
сопротивление Rн (рис.
4.11, й).
Преобразуем
параллельный участок С и RH в
эквивалентный последовательный с
помощью формул (3.56):
т.
е. при подключении высокоомной нагрузки
к контуру его резонансная частота
не изменяется, но увеличиваются потери
в контуре (рис. 4.11, б). При этом уменьшается
добротность Q’
= p/(R+RH’)
и увеличивается полоса пропускания
контура (4.10).
В
заключение следует отметить, что на
практике обычно используются
высокодобротные контуры, причем
низкоомные нагрузки подключаются к
контурам через различные согласующие
устройства (трансформаторы, повторители
и др.). Для получения высоких качественных
характеристик (большого входного и
низкого выходного сопротивлений, высокой
добротности, малой чувствительности
резонансной частоты и выходного сигнала
от нагрузки) применяют электронные
аналоги колебательных контуров,
реализуемых на базе зависимых
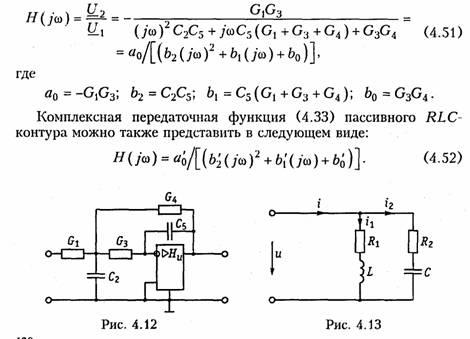
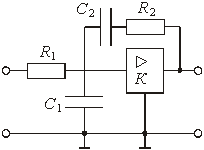
источников. На рис. 4.12 изображена схема
колебательного контура, реализованного
на базе ARC-звена,
второго порядка (рис. 3.37, а), где
принято Y1 = G1; Y2 =jωC2; Y3 = Gз; Y4 = G4; Y5 = jωC5.
При этом комплексная передаточная
функция цепи с учетом (3.138)
где т.
е. (4.52) совпадает с (4.51) с точностью до
постоянных множителей.
Таким
образом, с помощью рассмотренной активной
цепи можно получить электронный
аналог колебательного контура. На базе
активных элементов можно реализовать
и другие схемы электронных аналогов
колебательных контуров, важным
преимуществом которых является отсутствие
индуктивностей, высокое значение
добротности, слабо зависящей от нагрузки,
легкость перестройки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Свойства передаточных функций
Определение 1
Передаточная функция – это способ математического описания динамической системы.
Передаточная функция в основном используется в цифровой обработке сигналов, а также в теории управления. Она представляет собой дифференциальный оператор, который выражает связь между выходом и входом линейной стационарной системы. Если известны передаточная функция и входной сигнал системы, то можно восстановить выходной сигнал. В теории управления передаточная функция непрерывной системы является отношением преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.
Определение 2
Преобразование Лапласа – это интегральное преобразование, которое связывает между собой функцию комплексного переменного с функцией вещественного переменного.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Передаточная функция какой-либо системы определяет все ее динамические свойства, таким образом первоочередная задача расчета системы управления сводится к определению ее передаточной функции. К основным свойствам передаточных функций относятся:
- Импульсная переходная функция представляет собой оригинал для передаточной функции.
- В физически реализуемых системах порядок полинома числителя передаточной функции не может быть больше порядка полинома ее знаменателя.
- Числитель и знаменатель передаточной функции представляют собой характеристические полиномы дифференциального уравнения перемещения линейной системы. Полюса передаточной функции являются корнями характеристического полинома знаменателя, а нули корни характеристического полинома числителя.
- Для систем с неизменяемыми параметрами компонентов и с сосредоточенными параметрами передаточная функция представляет собой дробно-рациональную функцию
Передаточная функция электрической цепи. Пример решения задач
Передаточная функция линейной электрической цепи представляет собой отношение электрической выходной величины к входному воздействию, которые выражены в операторной форме и рассматриваются при нулевых начальных условиях, таким образом выражение передаточной функции выглядит следующим образом:
«Передаточная функция» 👇
$Н(р) = F2(p) / F1(p)$
где: F2 — выходная электрическая величина; F1 — входное воздействие.
Различают следующие основные виды передаточных функций для электрических цепей:
- Безразмерная (по напряжению) передаточная функция.
- Фазо-частотная характеристика.
- Амплитудно-частотная характеристика.
Общий вид передаточной функции по напряжению, которая очень часто используется для анализа электрических цепей частотными методами, следующий:
$H(jw) = F2(jw)/F1(jw)$
Рассмотрим схему электрической цепи, которая представлена на рисунке ниже:
Рисунок 1. Схема цепи. Автор24 — интернет-биржа студенческих работ
В комплексном виде передаточная функция для нее будет выглядеть следующим образом:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
В вышеприведенном выражении модуль:
$|Hu(jw)|=Hu(w)=U2(w) / U1(w)$
Рассмотрим схему, которая представлена на рисунке ниже
Рисунок 3. Схема. Автор24 — интернет-биржа студенческих работ
Необходимо определить коэффициент передачи по напряжению, а также амплитудно-частотную и фазо-частотную характеристики для вышеприведенной цепи. Для нее формула для расчета коэффициента передачи по напряжению будет иметь следующий вид:
$Hu(jw) = U2(jw) / U1(jw)$
Выражение комплексной функции U2(jw) будет иметь следующий вид:
$U2 = I(jw)*(1/jwC)=U1(jw) / (R+(1/jwC)) * 1/jwC = U1(jw) / (1+(jwRC)$
Если мы подставим формулу для U2 в выражение для Hu(jw), то получим комплексную передаточную функцию следующего вида:
$Hu(jw) = 1/(1+jwR*C)$
Таким образом амплитудно-частотную характеристику рассматриваемой цепи можно выразить:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Фазо-частотная характеристика определяется по формуле:
$фu = -arctgwR*C$
Если изменять частоту (w) от 0 до определенного значения, можно изобразить графики фазо-частотной и амплитудно-частотной характеристик.
Рисунок 5. Графики. Автор24 — интернет-биржа студенческих работ
Амплитудно-частотная и фазо-частотная характеристики могут быть представлены единым графиком, если построить зависимость комплексной передаточной функции от частоты w на комплексной плоскости. В данном случае конец вектора передаточной функции будет описывать кривую, называемую годографом комплексной передаточной функции.
Рисунок 6. График. Автор24 — интернет-биржа студенческих работ
В некоторых случаях оперируют таким понятием, как логарифмическая амплитудно-частотная характеристика
$К =20lgН(w)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
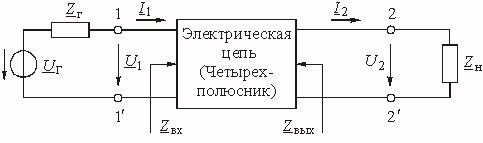
Электрическую цепь любой сложности, имеющую две пары зажимов для подключения к источнику и приемнику электрической энергии, в технике связи называют четырехполюсником. Зажимы, к которым подключается источник, называются входными, а зажимы, к которым присоединяется приемник (нагрузка) – выходными зажимами (полюсами).
В общем виде четырехполюсник изображают, как показано на рис. 1.1. К входу четырехполюсника 1–1′ подключен источник электрической энергии с комплексным действующим значением напряжения и внутренним сопротивлением
. К выходным зажимам 2–2′ присоединена нагрузка с сопротивлением
. К входным зажимам приложено напряжение с комплексным действующим значением
, к выходным – с комплексным действующим значением
. Через входные зажимы протекает ток с комплексным действующим значением
, через выходные зажимы – с комплексным действующим значением
. Заметим, что в роли источника и приемника электрической энергии могут выступать другие четырехполюсники.
Рис. 1.1
На рис. 1.1 использованы символические обозначения напряжений и токов. Это означает, что анализ электрической цепи проводится для гармонического колебания определенной частоты. Для данного гармонического колебания можно определить передаточную функцию нагруженного четырехполюсника, которая будет представлять собой отношение комплексного действующего значения выходной электрической величины к комплексному действующему значению входной электрической величины.
Если входным воздействием считать напряжение генератора с комплексным действующим значением , а реакцией четырехполюсника на это воздействие – напряжение с комплексным действующим значением
или ток с комплексным действующим значением
, то получаются комплексные передаточные функции общего вида:
, (1.1)
. (1.2)
В частных случаях, когда заданными воздействиями являются напряжение на входных зажимах четырехполюсника или ток, протекающий через эти зажимы, получают следующие четыре разновидности передаточных функций:
– комплексный коэффициент передачи по напряжению (для активных четырехполюсников, например усилителей, он носит название коэффициента усиления по напряжению);
– комплексный коэффициент передачи по току (для активных цепей – коэффициент усиления по току);
– комплексное передаточное сопротивление;
– комплексная передаточная проводимость.
Часто в теории цепей используют нормированную или рабочую передаточную функцию четырехполюсника:
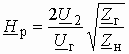
которая получается путем нормирования (1.1) множителем 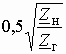
Как всякую комплексную величину Н можно представить в показательной форме:
, (1.4)
где – модуль комплексной передаточной функции, а j – ее аргумент.
Рассмотрим комплексную передаточную функцию по напряжению
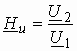
Подставляя в (1.5) запись комплексных действующих значений
,
получим
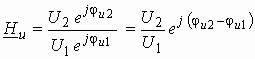
Из сравнения этого выражения с (1.4) видно, что
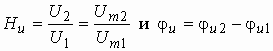
т. е. модуль комплексной передаточной функции по напряжению (или комплексного коэффициента усиления по напряжению) показывает во сколько раз изменяется действующее значение (амплитуда) гармонического колебания напряжения на выходе цепи по сравнению с аналогичным значением на входе цепи, а аргумент этой функции определяет сдвиг фаз между гармоническими колебаниями напряжения на входе и выходе.
Точно так же можно найти:
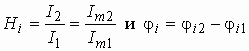
Все сказанное выше о коэффициенте передачи по напряжению справедливо и для коэффициента передачи по току.
Если мы будем изменять частоту гармонического колебания, то выражение (1.4) следует записать в виде:
. (1.6)
Функция частоты называется амплитудно-частотной характеристикой цепи (АЧХ). Она показывает какие изменения в амплитуды гармонических колебаний вносит цепь на каждой частоте.
Функция частоты называется фазо-частотной характеристикой цепи (ФЧХ). Соответственно эта характеристика показывает какой фазовый сдвиг приобретает гармоническое колебание каждой частоты при распространении по цепи.
Комплексную передаточную функцию можно представить также в алгебраической форме:
,
где Re и Im означают реальную и мнимую части комплексной величины.
Из теории комплексных величин известно, что
Пример 1.1
Определить коэффициент передачи по напряжению , АЧХ и ФЧХ цепи, изображенной на рис. 1.2, а.
Согласно (1.5) запишем
.
Найдем комплексную функцию на выходе цепи:
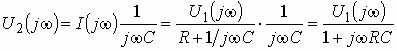
Подставив в формулу для
, получим комплексную передаточную функцию:
;
Рис. 1.2
АЧХ цепи
;
ФЧХ цепи
.
Изменяя частоту w от 0 до Ґ , можем изобразить графики АЧХ и ФЧХ цепи (рис. 1.2, б и в).
АЧХ и ФЧХ цепи можно представить единым графиком, если построить зависимость комплексной передаточной функции от частоты w на комплексной плоскости. При этом конец вектора
опишет некоторую кривую, которая называется годографом комплексной передаточной функции (рис. 1.3).
Рис. 1.3
Часто специалисты оперируют понятием логарифмической амплитудно-частотной характеристики (ЛАХ):
.
Значения величины К оцениваются в децибелах (дБ). В активных цепях, содержащих усилители, величину К называют еще логарифмическим усилением. Для пассивных цепей вместо коэффициента усиления вводят понятие ослабления цепи:
, (1.7)
которое также оценивается в децибелах.
Пример 1.2
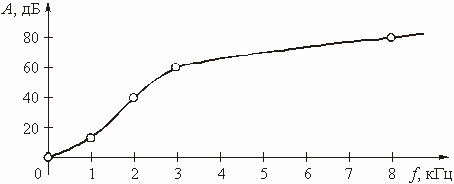
Известно, что модуль коэффициента передачи по напряжению цепи принимает следующие значения:
f = 0 кГц Н(f) = 1
f = 1 кГц Н(f) = 0,3
f = 2 кГц Н(f) = 0,01
f = 4 кГц Н(f) = 0,001
f = 8 кГц Н(f) = 0,0001
Рис. 1.4
Изобразить график ослабления цепи.
Значения ослабления цепи, рассчитанные по (1.7), приведены в таблице:
|
f, кГц |
0 |
1 |
2 |
4 |
8 |
|
А(f), дБ |
0 |
12 |
40 |
60 |
80 |
График А(f) приведен на рис. 1.4.
Если вместо комплексных сопротивлений емкости и индуктивности
иметь дело с операторными сопротивлениями емкости
и индуктивность pL, то в выражении
нужно заменить
на р.
Операторная передаточная функция цепи может быть записана в общем виде как дробно-рациональная функция с вещественными коэффициентами:
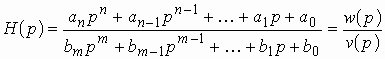
или в виде
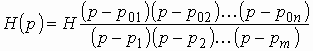
где – нули;
– полюсы передаточной функции;
.
Заменив в (1.8) оператор р на jw , вновь получим комплексную передаточную функцию цепи
,
где АЧХ цепи
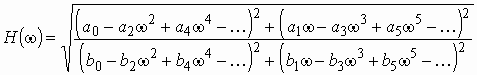
ФЧХ цепи
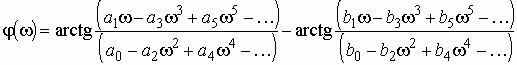
Учитывая, что является иррациональной функцией, обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:
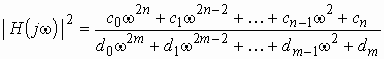
где коэффициенты получаются путем объединения коэффициентов при одинаковых степенях переменной w .
Пример 1.3
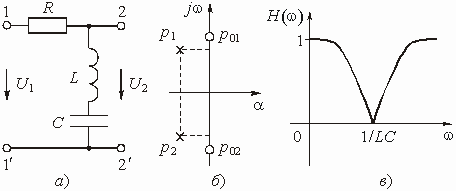
Найти коэффициент передачи по напряжению и квадрат АЧХ цепи, изображенной на рис. 1.5, а.
Коэффициент передачи по напряжению этой цепи равен
где Н = 1, ,
.
Корни числителя этой рациональной дроби, т. е. нули передаточной функции,
.
Корни знаменателя, или полюсы передаточной функции,
Рис. 1.5
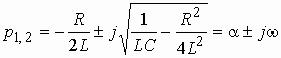
На рис. 1.5, б показано расположение нулей и полюсов функции при .
По теореме Виета
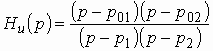
Амплитудно-частотная характеристика определяется из путем замены р на
и вычисления модуля полученной функции
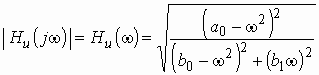
Квадрат АЧХ запишется в виде
где ;
;
;
.
АЧХ цепи изображена на рис. 1.5, в.
Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей:
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточной функции располагаются в левой полуплоскости комплексной переменной р. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции . Выберем входное воздействие
или в операторной форме
. Изображение выходного напряжения
в этом случае численно равно
, т. е.
где – полином числителя передаточной функции;
– коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
Перейдем от изображения к оригиналу
:
, (1.13)
где в общем случае .
В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (1.13) вещественные части полюсов должны быть отрицательными
, т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. n Ф m. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией переменной w с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.
5. Квадрат АЧХ не может принимать отрицательных и бесконечно больших значений при w > 0. Неотрицательность следует из свойств квадрата модуля комплексной величины. Конечность значений АЧХ на реальных частотах объясняется так же, как и в свойстве 3.
В большинстве цепей с зависимыми источниками имеется по крайней мере два пути прохождения сигнала: прямой (от входа к выходу) и обратный (с выхода на вход). Обратный путь прохождения сигнала реализуется с помощью специальной цепи обратной связи (ОС). Таких путей, а значит и цепей ОС, может быть несколько. Наличие в цепях с зависимыми источниками ОС придает им новые ценные качества, которыми не обладают цепи без ОС. Например, с помощью цепей ОС можно осуществить температурную стабилизацию режима работы цепи, уменьшить нелинейные искажения, возникающие в цепях с нелинейными элементами и т. д.
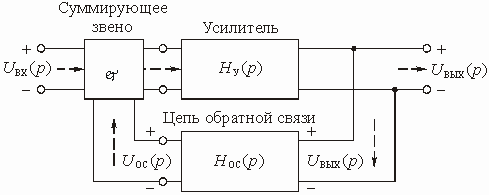
Любую цепь с обратной связью можно представить состоящей из двух четырехполюсников (рис. 1.6).
Рис. 1.6
Активный линейный четырехполюсник с передаточной функцией по напряжению является усилителем. Его иногда называют основным элементом цепи и говорят, что он образует канал прямого усиления.
Пассивный четырехполюсник с передаточной функцией по напряжению называется цепью обратной связи. На входе цепи осуществляется суммирование входного напряжения
и напряжения обратной связи
.
Выведем формулу передаточной функции по напряжению цепи, изображенной на рис. 1.6. Пусть на вход подается напряжение . Его операторное изображения
. На выходе цепи возникает напряжение
. В соответствии с рис. 1.6 его операторное изображение
. (1.14)
Операторное изображение можно записать через передаточную функцию
цепи обратной связи
.
Тогда выражение (1.14) можно переписать в виде
или
. (1.15)
Операторная передаточная функция по напряжению цепи с ОС (см. рис. 1.6).
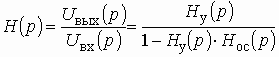
Пример 1.4
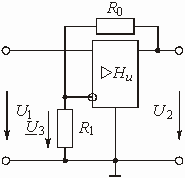
На рис. 1.7 изображена цепь на операционном усилителе (ОУ), предназначенная для масштабирования напряжения. Найти передаточную функцию этой цепи.
Получим передаточную функцию этой цепи как цепи с обратной связью, используя формулу (1.16).
Цепью обратной связи на схеме рис. 1.7 служит Г-образный делитель напряжения, составленный из резистивных сопротивлений и
. Выходное напряжение усилителя
поступает на вход цепи ОС; напряжение ОС
снимается с резистора
. Передаточная функция по напряжению цепи ОС
Рис. 1.7
.
Воспользуемся формулой (1.16) и учтем, что входное напряжение и напряжение обратной связи
не суммируются, а вычитаются. Тогда получим передаточную функцию масштабного усилителя:
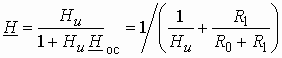
Учитывая, что в реальных ОУ значение >> 1, окончательно имеем:
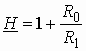
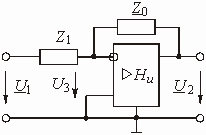
Пример 1.5
Звено на ОУ с частотно-зависимой ОС представлено на рис. 1.8. Найти передаточную функцию этого звена.
Рис. 1.8
Чтобы проанализировать прямой путь прохождения сигнала и путь прохождения сигнала ОС, необходимо воспользоваться методом наложения. Для этого следует поочередно исключать источники входного напряжения и напряжения обратной связи, заменяя их внутренним сопротивлением. В случае идеальных источников напряжения их внутреннее сопротивление равно нулю. Напряжение , приложенное к звену, ослабляется входной цепью, представляющей собой Г-образный делитель напряжения с сопротивлениями
и
в плечах. Передаточная функция по напряжению такого делителя равна
.
Цепь обратной связи также является Г-образным четырехполюсником с передаточной функцией.
Коэффициент усиления ОУ .
В соответствии с формулой (1.16) получаем передаточную функцию звена:
Учитывая, что >> 1, получаем:
.
Данное звено может выполнять различные функции в зависимости от вида сопротивлений и
. При
и
звено превращается в инвертирующий масштабный усилитель; при
и
– в интегратор; при
и
– в дифференциатор.
Пример 1.6
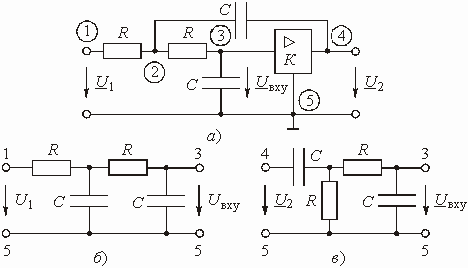
Звено второго порядка с регулируемым коэффициентом усиления представлено на рис. 1.9, а. Найти передаточную функцию этого звена.
Анализ прохождения входного сигнала и сигнала в цепи ОС показывает, что звено имеет входную цепь, изображенную на рис. 1.9, б и цепь ОС, показанную на рис. 1.9, в. Передаточные функции этих цепей можно получить матричным методом, например, рассматривая каждую цепь как каскадное соединение соответствующих Г-образных четырехполюсников.
Рис. 1.9
Для входной цепи
. (1.17)
Для цепи ОС
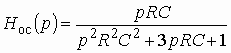
С учетом (1.16) получим передаточную функцию звена
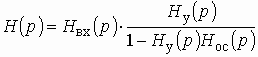
Коэффициент передачи усилителя . Тогда, подставляя (1.17) и (1.18) в (1.19), после преобразования имеем
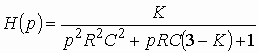
Переходя в (1.16) от оператора р к оператору , получаем комплексную передаточную функцию
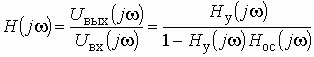
Произведение представляет собой комплексную передаточную функцию усилителя и цепи обратной связи при условии, что обратная связь разорвана (рис. 1.10). Функцию
называют передаточной функцией по петле ОС или петлевым усилением. Введем понятия положительной и отрицательной обратной связи. Эти понятия играют заметную роль в теории цепей с обратной связью.
Рис. 1.10
Предположим вначале, что передаточные функции ,
,
не зависят от частоты и являются вещественными числами. Такая ситуация возможна, когда в цепи отсутствуют LC-элементы. При этом
может быть как положительным, так и отрицательным числом. В первом случае сдвиг фаз между входным и выходным напряжениями или, другими словами, сдвиг фаз по петле обратной связи равен нулю или
, k = 0, 1, 2, … Во втором случае, когда
, сдвиг фаз по этой петле равен
или
.
Если в цепи с обратной связью сдвиг фаз по петле равен нулю, то обратная связь называется положительной, если же сдвиг фаз равен , то такая обратная связь называется отрицательной.
Передаточную функцию можно изобразить в виде векторов и показать их на комплексной плоскости. При положительной обратной связи вектор
находится на положительной вещественной полуоси, а при отрицательной обратной связи – на отрицательной вещественной полуоси.
Кривая, которую описывает конец вектора при изменении частоты w (рис. 1.11), называется, как известно, годографом.
Рис. 1.11
Представление в виде годографа позволяет определить вид обратной связи в случае частотнозависимой обратной связи.
Обратная связь называется положительной, если годограф лежит в правой, и отрицательной – если в левой полуплоскости комплексной плоскости. Отрицательная ОС применяется для стабилизации коэффициента усиления, подавления паразитных сигналов, коррекции частотных характеристик; положительная ОС может являться причиной неустойчивости цепи.
Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения. Таким образом, для определения условий устойчивости цепи достаточно найти характеристическое уравнение и его корни. Как видим, условия устойчивости можно определить и не вводя понятие обратной связи. Однако здесь возникает ряд проблем. Дело в том, что вывод характеристического уравнения и определение его корней являются громоздкой процедурой, особенно для цепей высокого порядка. Введение понятия обратной связи облегчает получение характеристического уравнения или даже дает возможность обойтись без него. Крайне важно и то, что понятие обратной связи адекватно физическим процессам, возникающим в цепи, поэтому они становятся более наглядными. Глубокое понимание физических процессов облегчает работу по созданию автогенераторов, усилителей и т. д.
Рассмотрим цепь (см. рис. 1.6) и выведем ее характеристическое уравнение. Пусть и, значит,
. Тогда из (1.15) следует:
. (1.21)
Здесь (в противном случае цепь нельзя считать возбужденной) и поэтому равенство (1.21) выполняется при условии
. (1.22)
Если записать передаточную функцию основной цепи в виде , а цепи ОС –
, то уравнение (1.22) перепишется следующим образом:
.
Это равенство выполняется при
. (1.23)
Выражение в левой части этого равенства является полиномом, поэтому (1.23) можно записать в общем виде:
. (1.24)
Это и есть характеристическое уравнение цепи.
Корни уравнения (1.24) в общем случае являются комплексными величинами
где . Зная корни характеристического уравнения, можно записать выходное напряжение:
. (1.25)
Чтобы напряжение не возрастало безгранично, всем корням
характеристического уравнения необходимо иметь отрицательные вещественные части, т. е. корни должны располагаться в левой полуплоскости комплексной переменной
. Цепь с ОС, обладающая такими свойствами, называется абсолютно устойчивой.
При исследовании цепей с обратной связью могут возникать две проблемы. Если проектируемая цепь должна быть устойчивой, то необходимо располагать критерием, который по виду функций и
позволял бы судить об отсутствии корней характеристического уравнения в правой полуплоскости р. Если обратная связь используется для создания неустойчивой автоколебательной цепи, то следует убедиться, что корни уравнения (1.24) расположены, наоборот, в правой полуплоскости. При этом необходимо иметь такое расположение корней, при котором самовозбуждение происходило бы на требуемой частоте.
Рассмотрим критерий устойчивости цепи, названный критерием Найквиста, и позволяющий судить об устойчивости цепи с обратной связью по свойствам разомкнутой цепи (рис. 1.10).
Передаточная функция разомкнутой цепи, или петлевое усиление, входит в характеристическое уравнение (1.22):
, (1.26)
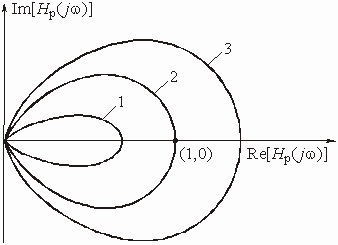
Если найдется такая частота w , для которой конец вектора попадает в точку с координатами (1, j0), то это будет означать, что выполняется условие (1.26), т. е. на этой частоте в цепи произойдет самовозбуждение. Значит, по годографу можно определить, устойчива цепь или нет. Для этого используется критерий Найквиста, который формулируется следующим образом: если годограф передаточной функции разомкнутой цепи не охватывает точку с координатами (1, j0), то при замкнутой цепи обратной связи цепь является устойчивой. В том случае, когда годограф
охватывает точку (1, j0), цепь неустойчива. На рис. 1.11 показаны годографы трех цепей с положительной обратной связью (цифра 1 соответствует годографу устойчивой цепи).
Пользуясь критерием Найквиста, легко получить условия самовозбуждения цепи с ОС. Запишем выражение для в виде
,
где ,
– модули передаточных функций;
,
– фазовые сдвиги соответственно в основном элементе и в цепи ОС.
Условия пересечения годографом оси абсцисс при
Х 1 можно записать в виде двух условий:
- условие (уравнение) баланса фаз
, где n = 0, 1, 2, …;
- амплитудное условие
Х 1, или
Х 1.
Выполнение неравенства соответствует режиму возникновения колебаний с нарастающей амплитудой, что характерно для начального этапа самовозбуждения. Выполнение равенства соответствует режиму генерации гармонического напряжения на частоте с постоянной амплитудой и носит название баланса амплитуд.
Как будет показано ниже, уравнение баланса фаз позволяет определить частоту, на которой происходит самовозбуждение цепи с ОС, а уравнение баланса амплитуд дает возможность определить величину амплитуды генерируемого колебания с частотой
в стационарной режиме.
Пример 1.7
Исследуем устойчивость цепи, изображенной на рис. 1.9, а. В ней можно выделить усилительный элемент с передаточной функцией и цепь обратной связи (рис. 1.9, в) с передаточной функцией (1.18)
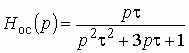
где .
Кроме того, напомним, что на усилитель сигнал поступает через входную цепь (рис. 1.9, б), передаточная функция которой (см. (1.17))
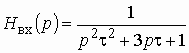
Получим характеристическое уравнение цепи:
или
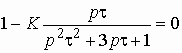
Откуда окончательно получаем
.
Корни этого характеристического уравнения
зависят от коэффициента усиления усилителя К. Расположение корней и
на плоскости комплексного переменного р для разных коэффициентов усиления и соответствующие этому графики свободных колебаний в цепи показаны на рис. 1.12.
Устойчивость данной цепи можно исследовать и с помощью критерия Найквиста. Комплексная передаточная функция разомкнутой цепи равна
Рис. 1.12
На рис. 1.11 приведены годографы устойчивой (К = 2, кривая 1) и неустойчивой (К = 3, кривая 2; К = 4, кривая 3) цепи.
Вопросы и задания для самопроверки
1. Что такое комплексная передаточная функция? Какие виды комплексных передаточных функций четырехполюсника известны?
2. Определить коэффициент передачи по напряжению , АЧХ и ФЧХ цепи, изображенной на рис. 1.2, а, если выходным напряжением является напряжение на резисторе R. Построить графики АЧХ и ФЧХ.
Ответ: 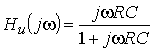
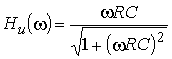
90° – arctg wRC.
3. Определить коэффициент передачи по напряжению при холостом ходе и коэффициент передачи по току при коротком замыкании для П-образного четырехполюсника в продольную ветвь которого включена индуктивность L, а в поперечные ветви – емкость С. Ответ: 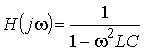
4. Определить ослабление, вносимое цепью рис. 1.2, а, при R = 31,8 кОм и = 10 кОм.
Ответ: 12 дБ.
5. Что такое операторная передаточная функция? Как она связана с комплексной передаточной функцией? Как определить нули и полюсы операторной передаточной функции?
6. Определить операторную передаточную функцию, комплексный коэффициент передачи по напряжению, АЧХ и квадрат АЧХ последовательного колебательного контура, изображенного на рис. 1.5, а, если выходным напряжением является напряжение на емкости С. Построить график АЧХ цепи.
Ответ: 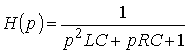
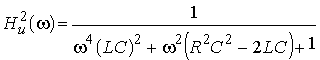
7. Перечислить основные свойства операторных передаточных функций пассивных цепей.
8. Как рассчитывается передаточная функция цепи с обратной связью?
9. Доказать, что операторная передаточная функция дифференциатора на операционном усилителе равна (–pRC). Построить график АЧХ такого дифференциатора.
10. Рассчитать передаточную функцию каскадного соединения цепей, изображенных на рис. 1.2, а и 1.7. Построить график АЧХ полученной цепи.
11. Определить передаточную функцию фильтра, изображенного на рис. 1.13.
Рис. 1.13
Ответ: 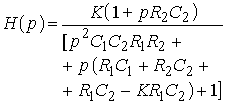
12. Что такое годограф петлевого усиления? Как по годографу определить тип обратной связи?
13. Как формулируется критерий устойчивости Найквиста? Для каких цепей он используется?
14. Определить комплексную передаточную функцию разомкнутой цепи, изображенной на рис. 1.13. Исследуйте зависимость устойчивости цепи от величины коэффициента усиления К.
Ответ: 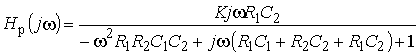
Содержание:
Операторные передаточные функции:
Практический смысл и назначение операторного метода в теории электрических цепей состоит, прежде всего, в представлении соотношения вход/выход в операторной форме, что даёт возможность существенно упростить процедуры анализа и синтеза электрических цепей и обеспечить связь между временным и частотным описаниями как колебаний, действующих в цепи, так и самой цепи.
Законы Ома и Кирхгофа в операторной форме
Покажем, что решение задач анализа колебаний в электрической цепи существенно упрощается при использовании операторного метода.
Законы Кирхгофа в операторной форме
Пусть токи
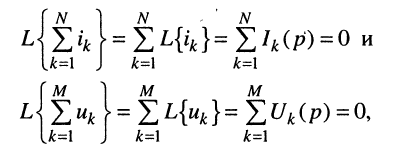
что говорит о формальной справедливости законов Кирхгофа для токов и напряжений, выраженных в операторной форме.
Операторные сопротивления и проводимости элементов электрических цепей
Убедимся в справедливости закона Ома для L-изображений колебаний на зажимах элементов R, L, С при нулевых начальных условиях (см.разд. 15.2) и найдём операторные изображения 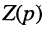
Для элемента активного сопротивления
откуда
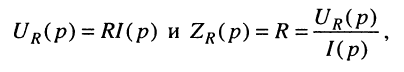
т. е. операторное активное сопротивление равно самому активному сопротивлению, поэтому операторная активная проводимость равна самой активной проводимости
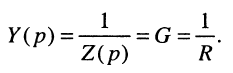
Для элемента индуктивности
правило дифференцирования даёт:
откуда операторные сопротивление и проводимость индуктивности равны:
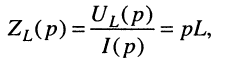
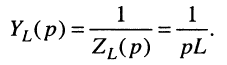
Для элемента ёмкости
правило интегрирования даёт:
откуда операторные сопротивление и проводимость ёмкости равны:
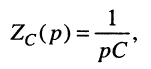
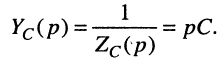
Заметим, что поскольку оператор р согласно (16.2) определён как комплексное переменное
операторные сопротивления и проводимости элементов L и С получаются заменой оператора 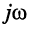
Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
Закон Ома при нулевых начальных условиях формально верен и для сложных двухполюсников, если в числе их элементов не содержатся независимые источники.
Определение:
Операторным сопротивлением 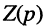
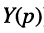
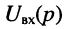
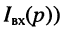
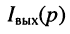
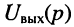
(соответственно 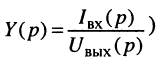
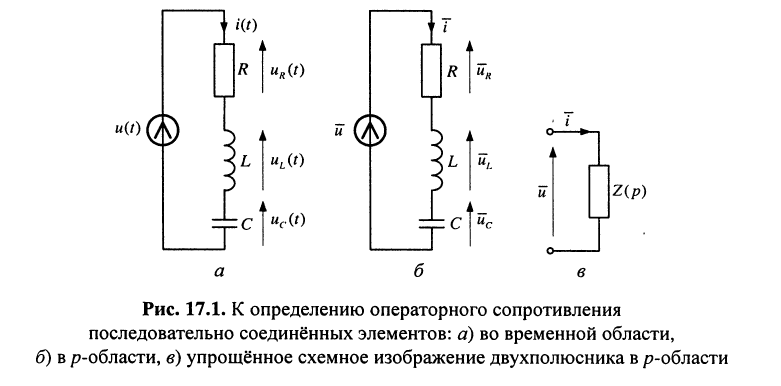
Пример 17.1.
Найти операторное сопротивление двухполюсника (рис. 17.1), состоящего из последовательно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Напряжение на зажимах двухполюсника при нулевых начальных условиях равно
Применим к полученному уравнению преобразование Лапласа:
откуда следует, что при последовательном соединении элементов их операторные сопротивления складываются, как и для комплексных сопротивлений, но оператор 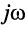
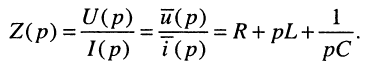
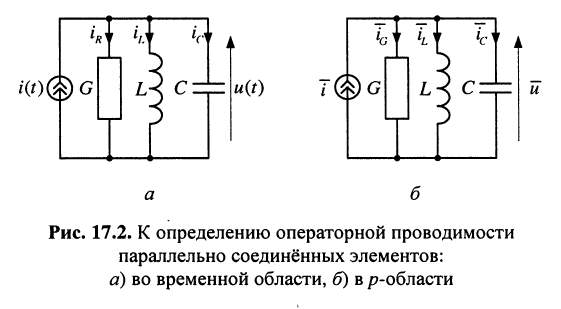
Пример 17.2.
Найти операторную проводимость двухполюсника (рис. 17.2), состоящего из параллельно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Для тока 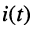
поэтому операторную проводимость заданного двухполюсника можно записать сразу:
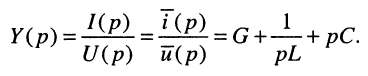
В силу дуальности последовательного и параллельного контуров выражение (17.9) можно было записать сразу на основании формулы (17.8).
Выражения (17.8) и (17.9) представляют собой входные операторные функции цепи. Они дают основания определению операторного сопротивления и проводимости двухполюсника общего вида.
Операторные сопротивление и проводимость двухполюсника общего вида
Закон Ома, при нулевых начальных условиях, формально можно применить и для сколь угодно сложных двухполюсников. Ранее
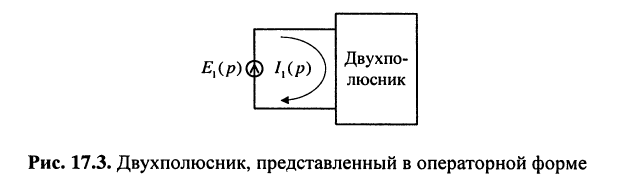
(см. лекцию 5) было установлено, что если на входе двухполюсника действует источник напряжения с ЭДС 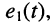
Переходя к L-изображениям напряжений, токов и сопротивлений элементов цепи, получим представление двухполюсника в операторной форме (рис. 17.3), что позволяет записать L-изображение входного тока:
Теперь согласно определению операторной проводимости и операторного сопротивления имеем:
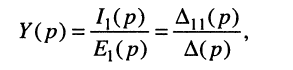
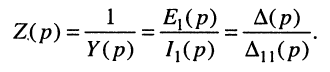
При этом нужно помнить, что определители и алгебраические дополнения в таких формулах записываются с учётом свойств преобразования Лапласа, как это сделано в примерах 17.1 и 17.2.
Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
В лекции 15 было показано, что во временной области соотношение вход/выход линейной электрической цепи при произвольном воздействии описывается уравнением свёртки:
где h(t) — импульсная характеристика, x(t) — воздействие, y(t) — реакция. При этом воздействие и реакция могут быть напряжениями или токами.
Для описания соотношения вход/выход в операторной форме воспользуемся L-изображением свёртки
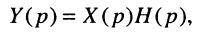
откуда получаем соотношения вход/выход в операторной форме
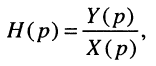
которое называют передаточной функцией.
Определение:
Передаточной функцией линейной электрической цепи называется отношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.
Выражение (17.13) говорит о том, что передаточная функция является L-изображением импульсной характеристики, т. е. импульсная характеристика является обратным преобразованием Лапласа передаточной функции:
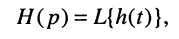
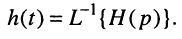
Именно этими зависимостями объясняется содержащееся в определении передаточной функции требование нулевых начальных условий.
Связь между передаточной функцией и переходной характеристикой можно установить, если воспользоваться интегралом Дюамеля (15.20а) при нулевых начальных условиях:
когда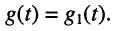
Первый сомножитель правой части полученного уравнения содержит L-изображение производной, поэтому окончательно можно записать:
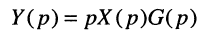
и
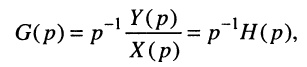
что полностью соответствует связи импульсной и переходной характеристик (15.16).
Обратим внимание на то, что передаточная функция может быть получена из комплексных частотных характеристик формальным образом, а именно — простой заменой в КЧХ 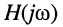
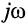
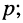
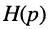
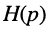
В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве реакции цепи, различают четыре вида передаточных функций:
операторное передаточное сопротивление
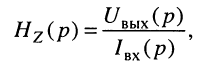
операторную передаточную проводимость
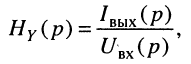
передаточную функцию по току
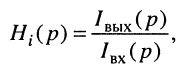
передаточную функцию по напряжению
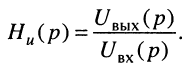
Последние две функции иногда называют операторными передаточными коэффициентами по току и по напряжению соответственно.
По любой из передаточных функций (17.18)—(17.21) нетрудно найти L-изображение реакции цепи, а затем и саму реакцию на заданное воздействие, поскольку любая передаточная функция Н(р) согласно (17.12) может рассматриваться как связующий коэффициент между L-изображения ми воздействия Х(р) и реакции Y(p).
Пример 17.3.
Записать передаточную функцию для последовательного колебательного контура (рис. 17.1, б) относительно напряжения на индуктивности.
Решение. По определению передаточной функции для индуктивности имеем
Но операторное напряжение на индуктивности равно:
поэтому
Подставляя сюда операторное сопротивление (17.8), получаем искомую передаточную функцию:
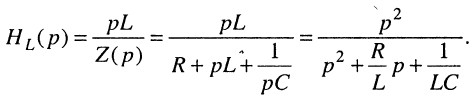
Аналогично можно получить и другие передаточные функции для последовательной, параллельной или более сложной цепи. В последнем случае потребуется составить систему уравнений для L-изображений колебаний, воспользовавшись методом контурных токов или узловых напряжений.
Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
Задача 17.1.
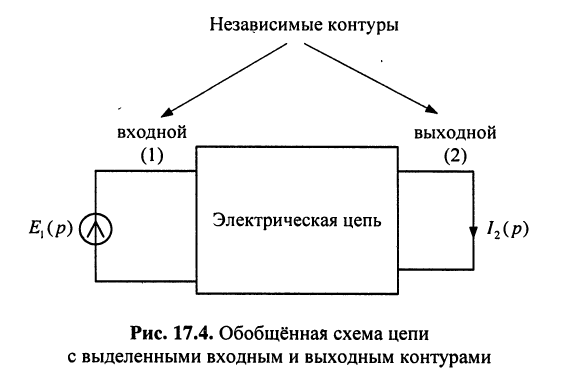
Получить и исследовать общее выражение для передаточной функции цепи, когда воздействие представляет собой ЭДС источника напряжения, а реакцией является ток в выделенной ветви анализируемой цепи (рис. 17.4).
Решение. Выберем независимые контуры в цепи так, чтобы через источник напряжения замыкался ток только одного входного контура, а через интересующую нас ветвь — ток только одного выходного контура. На рис. 17.4 они обозначены индексами 1 и 2 соответственно.
Теперь, как и в задаче 5.2, необходимо положить 
откуда по определению передаточной функции имеем операторную передаточную проводимость
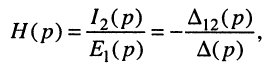
где 
a 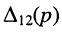
Заметим, что определитель и все его миноры представляют собой рациональные функции оператора р, все коэффициенты которых являются вещественными числами. Это объясняется тем, что при раскрытии определителя над его элементами совершаются только операции умножения, сложения и вычитания, а сами элементы представляют собой простейшие рациональные
функции с вещественными коэффициентами вида (17.11). Раскрывая определитель 
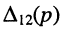
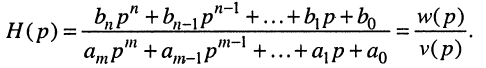
Полиномы числителя 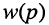
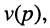
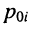
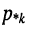
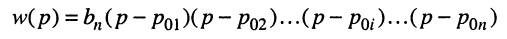
и
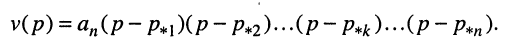
Отсюда передаточная функция (17.24) приобретает вид:
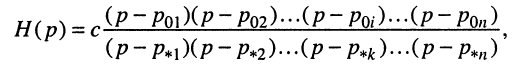
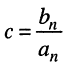
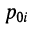
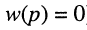
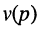
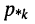
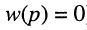
Названия корней уравнения 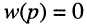
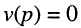
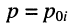
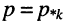
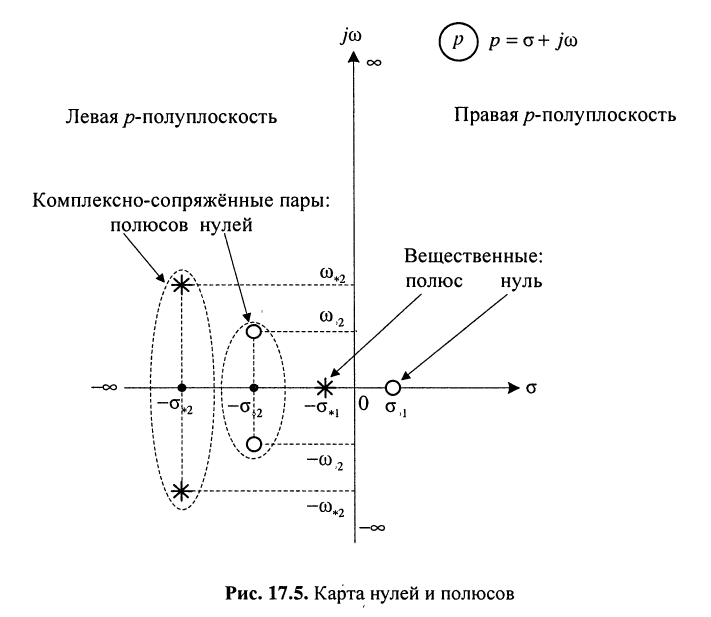
Нули и полюсы наглядно отображаются на комплексной p -плоскости (рис. 17.5) значками ( ° ) и ( * ) соответственно.
На рис. 17.5 показаны:
и 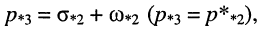
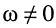
Отображение нулей и полюсов на p-плоскости называют картой нулей и полюсов. Различают левую и правую р-полуплоскости.
Карта нулей и полюсов позволяет оценить ряд свойств электрической цепи и, в частности, определить её устойчивость с точки зрения устойчивости передаточной функции.
Утверждение:
цепь является строго устойчивой тогда и только тогда, когда её передаточная функция имеет, полюсы только в левой р-полуплоскости, исключая мнимую ось.
Доказательство. Напомним, что цепь называется строго устойчивой, если при нулевых начальных условиях ограниченное по величине воздействие
вызывает ограниченную по величине реакцию
Но реакцию y(t) при нулевых условиях можно найти с помощью уравнения свёртки
Отсюда при заданных ограничениях имеем соотношение
из которого следует, что для получения равномерно ограниченной для всех t реакции, т. е. для обеспечения строгой устойчивости цепи должно выполняться условие абсолютной сходимости интеграла от импульсной характеристики:
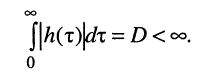
Найдём расположение полюсов, которое соответствует полученному условию. Для этого представим импульсную характеристику h(t) цепи как обратное L-изображение передаточной функции (17.15) путём разложения последней на сумму простых дробей (16.28):
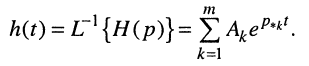
Подставим в интеграл (17.28) правую сумму (17.29)
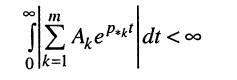
и проведём ряд несложных преобразований.
Поскольку модуль суммы не превосходит суммы модулей, справедливо следующее неравенство:
которое проинтегрируем:
В правой части полученного неравенства поменяем местами знаки суммирования и интегрирования и оставим только знак равенства:
Рассмотрим интеграл в правой части равенства, содержащий модуль экспоненты, при
Здесь, во-первых,
во-вторых, первая экспонента под интегралом всегда неотрицательна, поэтому знак модуля можно опустить:
Остаётся исследовать сходимость интеграла при положительном и отрицательном показателе
Сходимость интеграла при 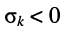
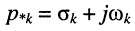
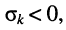
Связь передаточной функции с частотными и временными характеристиками цепи
Как было показано в лекции 10, для определения частотных характеристик АЧХ 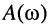
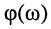
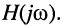
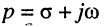
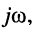
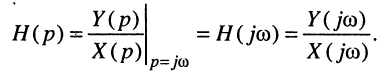
Отсюда имеем:
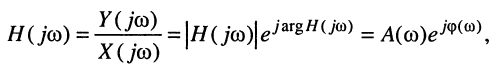
где
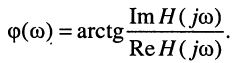
Эквивалентное выражение для КЧХ получается из (17.31), если воспользоваться комплексными функциями числителя и знаменателя:
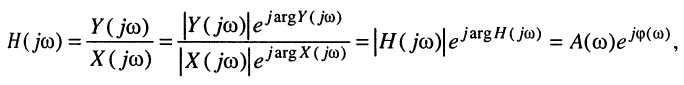
где
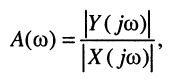
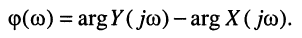
Вследствие того, что функция
является иррациональной, обычно при анализе и синтезе цепей используют квадрат АЧХ:
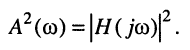
Перечислим основные свойства передаточных функций и квадрата АЧХ пассивных цепей.
- Передаточная функция является L-изображением импульсной характеристики.
- Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами.
- Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
- Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей; приневыполнении этого свойства АЧХ на бесконечно больших частотах
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
- Частотные характеристики цепи вычисляются по передаточной функции при подстановке
- Квадрат АЧХ является чётной рациональной функцией переменной с вещественными коэффициентами:
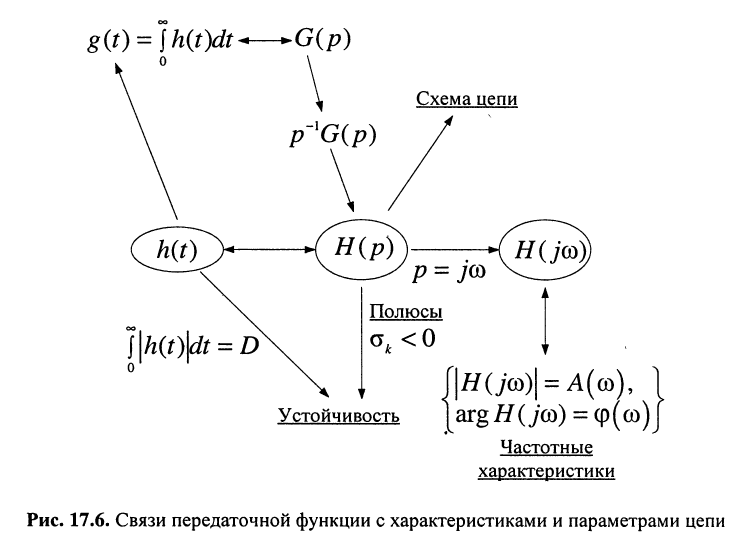
- По передаточной функции можно изобразить схему цепи
Обобщённая схема связи передаточной функции с характеристиками и свойствами цепи представлена на рис. 17.6.
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей


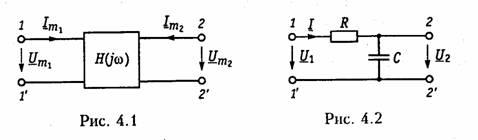

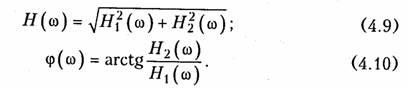
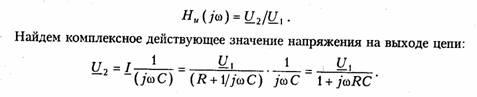
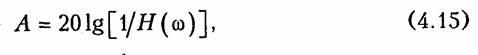



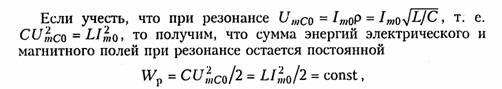


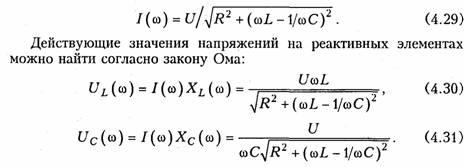
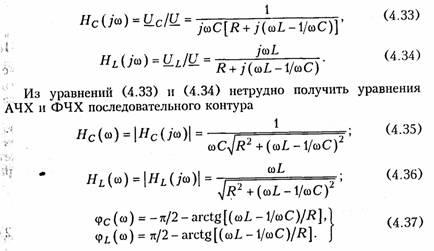
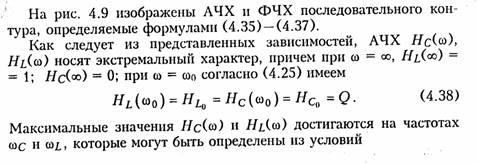

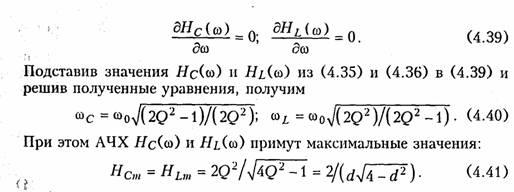
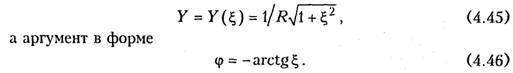

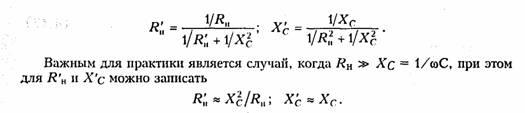










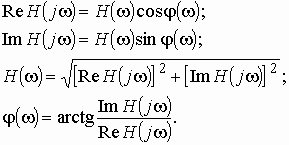
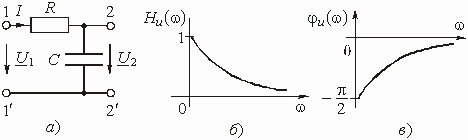
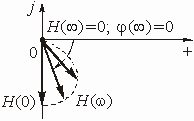


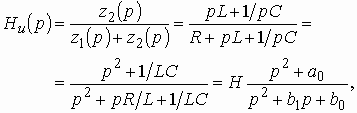
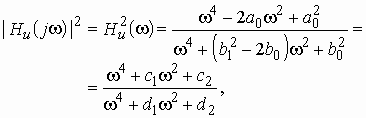

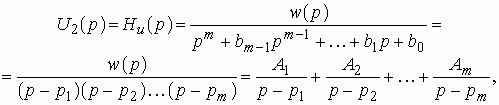

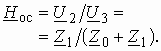
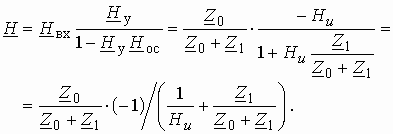

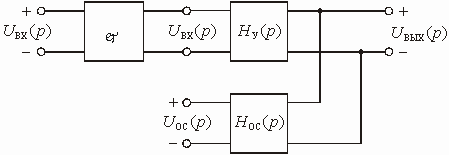

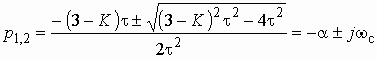
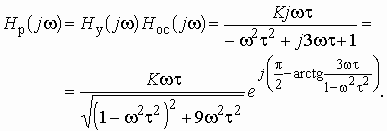
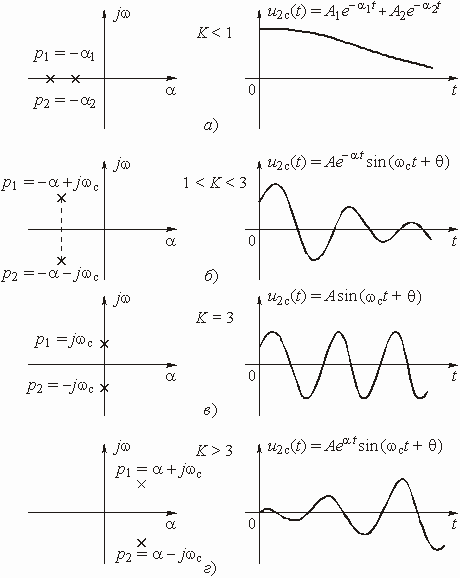
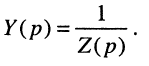
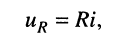
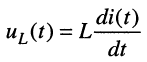
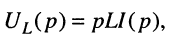
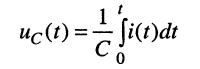
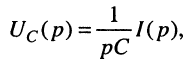
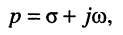
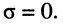
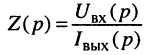
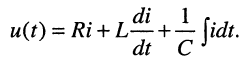
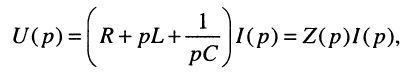
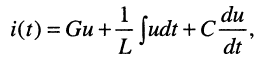
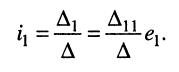
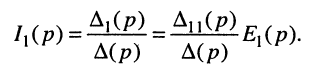
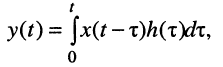
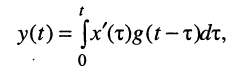
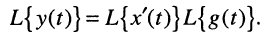
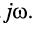
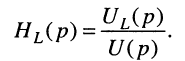
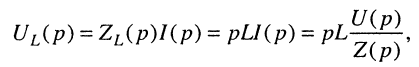
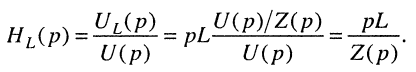
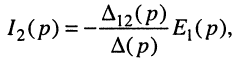
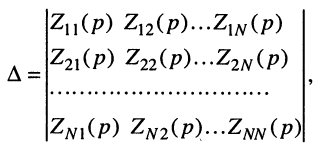
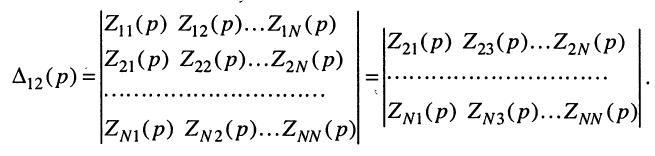
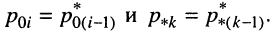
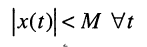
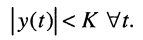
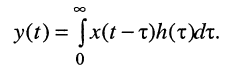
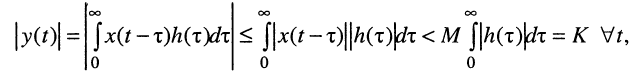
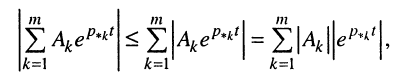
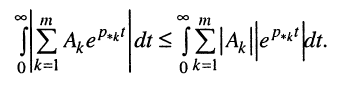
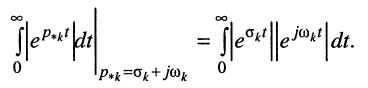
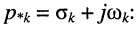
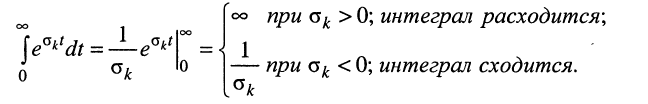
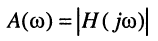
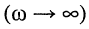 должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.