Переднее и заднее фокусные расстояния.
Р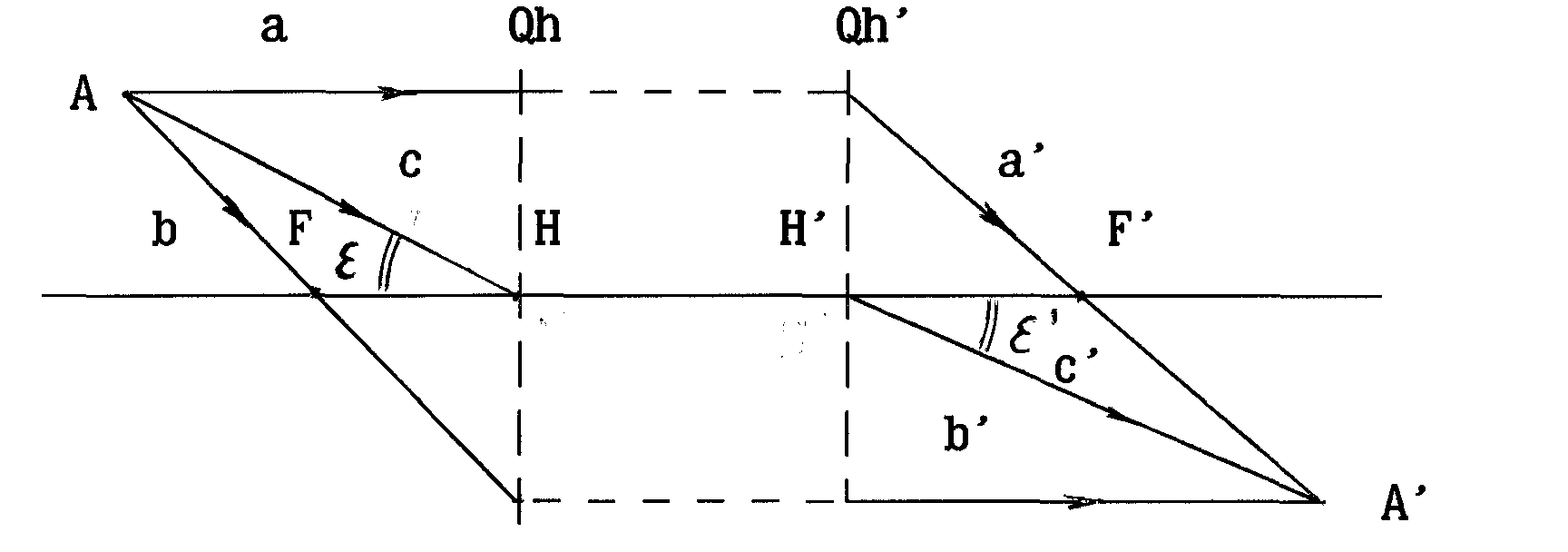
точкиНдо переднего фокусаFявляется передним фокусным расстоянием
оптической системы – f,
Рис.7. Графическое
определение положения главных плоскостей
и фокусов оптической системы: а — задних,
б — передних.
а расстояние
H‘F‘-от
задней главной точки Н’до заднего
фокусаF’ — задним фокусным
расстоянием f ′(рис.7).
Фокусные расстояния
отсчитывают от соответствующих главных
точек с учетом правила знаков. Если
оптическая система находится в однородной
среде, например в воздухе ( n=n‘ = 1), тоf ′ =
—f, т.е. фокусные расстояния равны по
абсолютному значению.
В общем случае –
f ′ / f
= n/n‘.Так какn > 0 иn‘
> 0, то фокусные расстояния всегда имеют
разные знаки.
Обычно оптическую
систему характеризуют задним фокусным
расстоянием, поэтому, если f
′ > 0,то система
считается положительной, если
f
‘< 0,то — отрицательной.
Узловые точки оптической системы.
Точки предмета и
изображения, лежащие на оптической оси,
для которых угловое увеличение равно
плюс единице (
= +1), называются узловыми точками
оптической системыNиN
Будем в дальнейшем
рассматривать только оптические системы
расположенные в однородной среде, для
которых n=n
,f
=f,
а следовательно, узловые точкиN,Nи главные точкиH,Hтакой системы
совпадают.
В этом случае
сопряженные лучи, проходящие через
главные точки HиHпараллельны друг другу (рис.8), т.е.
=‘.
Построение изображений и хода лучей в идеальной оптической системе.
Графическое решение
задачи построения изображения предмета
в оптической системе сводится к построению
изображения отдельных точек предмета,
а в конечном итоге к построению хода
лучей через оптическую систему. При
этом используются свойства кардинальных
элементов идеальной оптической
системы.Для построения любой точки
предмета достаточно построить ход хотя
бы двух лучей, проходящих через предметную
точку. Точка пересечения этих лучей
после прохождения их через оптическую
систему будет изображением предметной
точки.
Обычно для построения
используют так называемые характерные
лучи, ход которых в оптической системе
хорошо известен, т.е. лучи, проходящие
через фокусы и главные (узловые) точки
оптической системы
Луч (а),проходящий
через предметную точку (А) и падающий
на систему параллельно оптической оси,
после преломления на задней главной
плоскости (Oh)’проходит через задний фокус (F‘).
Луч (b),
проходящий через предметную точку и
передний фокус, после преломления на
передней главной плоскости идет
параллельно оптической оси.
Л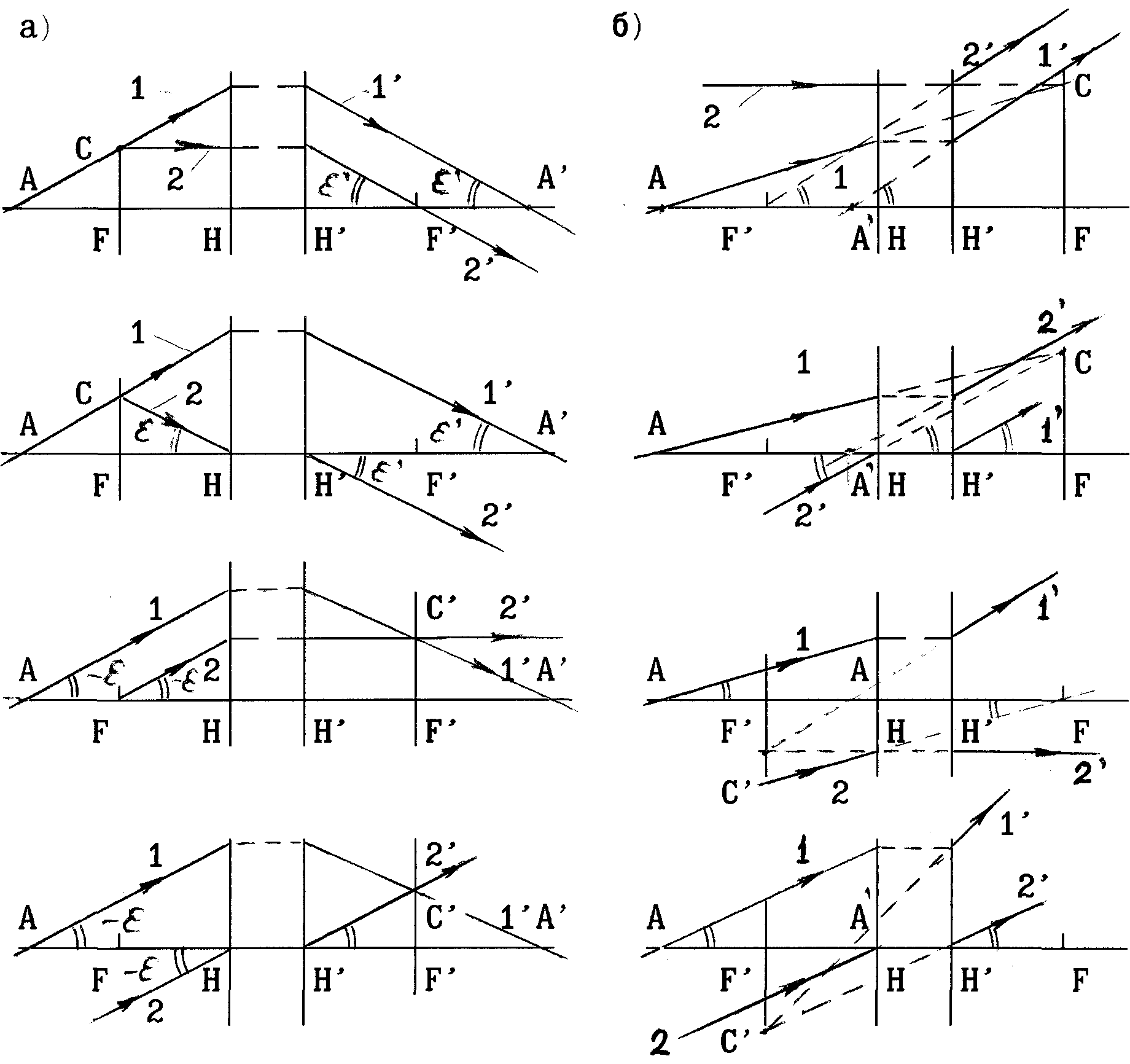
(c), проходящий через
предметную точку и переднюю главную
(узловую) точку, выходит из задней главной
(узловой) точки параллельно падающему
лучу (=)
.
Этими тремя лучами
удобно пользоваться, если предметная
точка расположена вне оптической оси.
Если же точка расположена на оптической
оси, то все три описанных выше луча
совпадают с оптической осью.
Поэтому для
построения изображения точки, расположенной
на оптической оси, необходимо построить
ход хотя бы одного луча, пересекающего
оптическую ось в предметной точке, и
найти точку пересечения этого луча
после выхода из оптической системы с
оптической осью. Эта точка и будет
изображением исходной предметной точки.
Рис.9. Построение
хода лучей в положительной (а) и
отрицательной (б) оптической системе.
1— заданный луч,2 —вспомогательный
луч.
На рис.9 показаны
четыре способа построения хода лучей
через положительную и отрицательную
оптические системы. Для построения
используются вспомогательные лучи,
проходящие через фокусы или главные
точки.
Точки, общие для
заданного и вспомогательного лучей в
передней фокальной плоскости, обозначены
точкой С,а точки общие для тех же
лучей в задней фокальной плоскости
обозначены соответственно через С‘.Лучи, выходящие из точек С,после
прохождения оптической системы будут
параллельными между собой. Параллельные
лучи, падающие на оптическую систему
соберутся в точке С’.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Переднее фокусное расстояние
Cтраница 1
Переднее фокусное расстояние / — расстояние от передней главной точки до переднего фокуса.
[1]
Проходящие через объект лучи света образуют за передним фокусным расстоянием окуляра 5 FOK действительное увеличенное и перевернутое изображение 1 объекта. Это изображение рассматривается через окуляр, для которого это изображение является объектом наблюдения. Таким образом, окуляр лишь увеличивает изображение, образуемое объективом, и никаких деталей наблюдаемого объекта выявить не может.
[2]
В случае объективов с большой апертурой и малым передним фокусным расстоянием освещение объекта производится с помощью микрообъектива, который в этом случае одновременно выполняет роль микроконденсора. Как это ясно из рисунка, она принципиально ничем не отличается от ранее рассмотренной схемы рис. 34, б, применяемой для освещения прозрачных объектов.
[3]
Гельмгольца, а [ 0 005 мм); f — переднее фокусное расстояние глаза, равное 15 4 мм.
[5]
Фокус F называется обычно передним фокусом, фокус F — задним фокусом; соответственно этому расстояние / называется передним фокусным расстоянием, расстояние / — задним фокусным расстоянием.
[7]
Фокус F называется обычно передним фокусом, фокус f — задппм фикусом; соответственно этому расстояние / называется передним фокусным расстоянием, расстояние / — задним фокусным расстоянием.
[9]
Фокус F называется обычно передним фокусом, фокус F — задним фокусом; соответственно этому расстояние / называется передним фокусным расстоянием, расстояние / — задним фокусным расстоянием.
[10]
При измерениях яркости поверхностей с направленно-рассеянным отражением, которые освещены несколькими источниками, оказываются существенными не только диаметр объектива и заднее фокусное расстояние, но также и переднее фокусное расстояние телескопической системы. Например, при наблюдении удаленного источника, свет которого отражается с некоторым рассеянием ( как и в случае зеркального отражения) от близко расположенной поверхности, отсчет яркости при фокусировке прибора на эту поверхность будет отличаться от отсчета, полученного при фокусировке на бесконечность. Следует сказать, что в общем случае наиболее точные результаты все-таки получаются при фокусировке на бесконечность.
[11]
Оно означает, что расстояние между главной плоскостью первой линзы в пространстве изображений и главной плоскостью второй линзы в пространстве объектов должно быть равно сумме заднего фокусного расстояния первой линзы и переднего фокусного расстояния второй линзы. Сравнение с (4.111) показывает, что это эквивалентно условию F FZ, но тогда формулы (4.100) и (4.105) дают для комбинированной системы бесконечно большое асимптотическое фокусное расстояние, что является критерием телескопической системы. Из (4.137) мы видим также, что в этом случае и расстояние между главными плоскостями бесконечно велико.
[13]
V, например, лежит слева от FI, то передняя главная плоскость HI расположена слева от F. Заметим также, что переднее фокусное расстояние системы выражается через передние фокусные расстояния двух линз, в то время как заднее фокусное расстояние системы явно зависит от задних фокусных расстояний линз.
[14]
V, например, лежит слева от FI, то передняя главная плоскость HI расположена слева от F. Заметим также, что переднее фокусное расстояние системы выражается через передние фокусные расстояния двух линз, в то время как заднее фокусное расстояние системы явно зависит от задних фокусных расстояний линз.
[15]
Страницы:
1
2
Фокусное расстояние
У центрированных оптических приборов (объективы, лупы, окуляры, очковые линзы и т.п.) есть пара замечательных точек: переднего и заднего фокусов. Эти точки на оптических схемах обозначают F и F’ соответственно. Параллельный пучок света пришедший вдоль оптической оси объектива собирается в точке заднего фокуса F’. Светящаяся точка расположенная в переднем фокусе F даст на выходе из объектива параллельный пучок света распространяющийся вдоль оптической оси. Обе эти точки лежат на оптической оси — оси симметрии центрированного оптического прибора.
Есть и еще одна пара замечательных точек на оптической оси объектива — так называемые главные точки: H — передняя и H’ — задняя. Расстояние от H до F — называют передним фокусным расстоянием f, а от H’ до F’ — задним фокусным расстоянием f’. Заметим, что для обычного объектива работающего в воздухе f’ — величина положительная, а f = -f’. Если известно положение этих точек, то возможно в приближении так называемых «нулевых лучей» построить изображение любой точки в пространстве предметов (грубо говоря, слева от оптической схемы). см. рисунок.
- cardinals.JPG (16.65 КБ) 18140 просмотров
Фокусные расстояния f’ и f (обычно выражаются в мм) — самые важные масштабные характеристики объективов. f’ определяет масштаб изображения, которое строится объективом:
y’ = f’·φ = f’·φo/57.3 = f’·φ’/(60·57.3) = f’·φ»/(60·60·57.3), (1)
где y’ — линейный размер изображения предмета небольшого углового размера φр (в радианах), или φо (в градусах), или φ’ (в угловых минутах*), или φ» (в угловых секундах).
или в обратном угловой размер предмета φ (радианы, градусы, минуты, секунды) который на приемнике имеет линейный размер y в мм:
φ (рад) = y/f’, (1.a)
φ°= 57.3*y/f’, (1.b)
φ’ = 57.3*60*y/f’ или примерно 3500*dy/f (1.c)
φ»= 57.3*60*60*y/f’ или примерно 200000*dy/f[/b] (1.d)
Например, размер диска Луны (φ = 30 угловых минут) в фокальной плоскости объектива с фокусным расстоянием f’ = 400 мм будет равен y’ = f’·φ/(60’·57.3o) = 400·30’/3438 = 3.5 мм. На кадр со сторонами 35х24 мм в фокусе астрографа с фокусным f’ = 150 мм поместится по этим формулам φ° = 57.3·y’/f’ поле зрения 13 на 9 градусов (57.3·35/150 и 57.3·24/150). Фокусное расстояние однозначно (с точностью до дисторсии) определяет доступное поле зрения объектива 2W = 2·arctg(Y’/f’), где 2W — угловое поле зрения, Y’ — половинка диагонали кадра или радиус полевой диафрагмы.
Фокусные расстояния линз (объективов) также позволяет рассчитывать ход лучей в оптических системах в так называемом нулевом приближении (см. «Полезные оптические соотношения» — формулы отрезков, Ньютона и прохождения луча через тонкую линзу).
*) В расчетной оптике величины относящиеся к пространству изображений (например заднее фокусное расстояние, задний фокус, размер изображения и т.д.) снабжают апострофом: f’, F’, y’ для того, чтобы отличать от точек и величин относящихся к пространству предметов: f, F, y.
- cardinalies.JPG (42.78 КБ) 18129 просмотров
Связь фокусного расстояния с доступным полем зрения телескопа
Для телескопа фокусное расстояние его объектива главным образом определяет величину доступного поля зрения. У более короткофокусных телескопов (обычно это рефракторы и телескопы по схеме Ньютона) доступное поле зрения шире. Более длиннофокусные телескопы (обычно это разнообразные Кассегрены) имеют более ограниченное входное поле зрения. Связь доступного поля зрения телескопа 2w (в градусах) с фокусным расстоянием его объектива f’ проста: 2w = 57.3*D/f’, где D — диаметр максимально возможной полевой диафрагмы окуляра. D ограничено диаметром окулярной трубки телескопа, в телескопах оборудованных 2″ фокусером это 46 мм, а в телескопах оборудованных 1.25″ фокусером 27 мм. На основе этой формулы получается такая вот табличка:
Доступные поля зрения в телескопах
с разными фокусными расстояниями
| fD | 2″/46 мм | 1.25″/27 мм |
| 250 мм | 10.5° | 6.2° |
| 500 мм | 5.3° | 3.1° |
| 750 мм | 3.5° | 2.1° |
| 1000 мм | 2.6° | 1.5° |
| 1250 мм | 2.1° | 1.2° |
| 1500 мм | 1.8° | 62′ |
| 1750 мм | 1.5° | 53′ |
| 2000 мм | 1.3° | 46′ |
| 2250 мм | 1.2° | 41′ |
Апертура
Апертура A и A’ другая базовая характеристика оптических приборов — она связана со способностью оптики ограничивать световые пучки, которые проходят через нее от предмета к изображению. Различают входную апертуру A (ограничение размеров световых пучков от предмета попадающих в оптических прибор) и выходную апертуру A’ (ограничение размеров световых пучков, которые строят изображение). И та и другая апертура связаны между собой и определяются явно или неявно заданной апертурной диафрагмой — механическим узлом оптического устройства выполненным в виде отверстия постоянного или переменного размера в непрозрачном материале, который максимально ограничивает осевой пучок света (который строит изображение на оптической оси). Роль апертурной диафрагмы может играть оправа линзы (не всегда первой), края зеркал и т.д. Иногда оптический узел «заимствует» апертурную диафрагму у другого, с которым он работает совместно (например, окуляр обычно не имеет своей апертурной диафрагмы). Входная (передняя) и выходная (задняя) апертура измеряются по-разному, в зависимости от того с каким предметом/изображением работает оптическое устройство. Входная апертура телескопа (удаленный предмет) это обычно диаметр осевого пучка D, а у микроскопа (близкий предмет) так называемая числовая апертура — синус угла, под которым выходит крайний луч из осевой точки предмета умноженный на показатель преломления среды. Чем апертура больше, тем меньше влияние дифракции и больше способность прибора собирать свет и строить более яркие изображения. Но чем больше апертура тем обычно больше влияние остаточных аберраций ухудшающих качество изображения, и тем более сложную конструкцию объектива приходится разрабатывать для контроля этих аберраций.
Зависимость проницания (M) и
разрешения (ф») от апертуры
телескопа (D в дюймах и мм)
| D,» | D,мм | M, зв.вел. | ф» |
| 3.1 | 80 | 12.0 | 1.50 |
| 3.9 | 100 | 12.5 | 1.20 |
| 5 | 127 | 13.0 | 0.94 |
| 6 | 152 | 13.4 | 0.79 |
| 7 | 180 | 13.8 | 0.67 |
| 8 | 203 | 14.0 | 0.59 |
| 10 | 254 | 14.5 | 0.47 |
| 12 | 305 | 14.9 | 0.39 |
| 14 | 356 | 15.3 | 0.34 |
| 16 | 407 | 15.5 | 0.29 |
| 18 | 457 | 15.8 | 0.26 |
| 20 | 508 | 16.0 | 0.24 |
В телескопе входная и выходная апертуры связаны между собой простым соотношением:
A = Г·A’, (2)
где A, мм — входная апертура (диаметр входного зрачка),
A’, мм — выходная апертура (диаметр выходного зрачка),
Г — увеличение
В объективе (фотообъективе, объективе телескопа) соотношение меняется:
A’ = 0.5·A/f’об, (3)
где A, мм — входная апертура объектива (ее диаметр),
A’, мм — выходная апертура (синус апертурного угла),
f’об — заднее фокусное расстояние объектива
Зрачки
Зрачок характеристика тесно связанная с апертурой. Выходной зрачок — это изображение апертурной диафрагмы последующей частью оптического прибора. А входной зрачок — изображение апертурной диафрагмы через предыдущую часть оптической системы в пространство предметов. Входная апертура у телескопа или объектива это диаметр входного зрачка D, выходная апертура телескопа или окуляра — диаметр его выходного зрачка D’. Так называемые главные лучи (средние лучи световых пучков) проходят через центр входного и выходного зрачка. При совместном использовании оптики, в которой есть свои апертурные диафрагмы следует добиваться совмещения соответствующих входных и выходных зрачков и согласовывать из размеры для предотвращения срезания внеосевых пучков. Простейший пример — визуальные наблюдения в телескоп, когда входной зрачок глаза наблюдателя (или просто — зрачок) следует совместить с выходным зрачком телескопа (окуляра).
Соотношения диаметров входного и выходного зрачков телескопа — см. формулу (2).
Разрешение
Разрешение — то минимальное расстояние между светящимися точками (линиями) в пространстве предметов или изображения, которое способен разрешить оптический прибор — построить изображение однозначно трактуемое как двойное. В зависимости от типа оптики это расстояние следует измерять в угловой (для «удаленных» предметов) или линейной (для «близких») мере. Для телескопа в пространстве предметов это минимальное угловое расстояние между равными по яркости компонентами двойной звезды, при котором между их изображениями еще виден темный промежуток. Обычно полагают, что звезды разрешены, если расстояние между максимумами в дифракционной картине изображения равно или больше радиусу первого темного кольца, при этом относительный провал яркости между максимумами составит 26% (критерий Рэлея). Визуальное разрешение при наблюдении в телескоп ограничено многими другими факторами кроме дифракции: недостаточным увеличением, дефектами зрения наблюдателя, аберрациями и ошибками изготовления объектива и окуляра, светорассеиванием, неоднородностями показателя преломления воздуха внутри и вне телескопа, недостаточно или избыточной яркостью объекта наблюдения, величиной центрального экранирования и т.д. Но только дифракция представляет собой по настоящему непреодолимое препятствие для разрешения, а все остальные факторы можно более или менее эффективно преодолеть. В таком идеализированном случае предел разрешения будет равен
ф» = 140″/D, (4)
где ф» — разрешение в угловых секундах, D — диаметр входной апертуры (зрачка) телескопа.
Есть и другие формулы в которых вместо 140″ используют коэффициент 120″ (5% провал яркости между максимумами), 114″ (плоская «полочка») и другие. Обычно эту величину и приводят производители телескопов, хотя, возможно, и не совсем правомерно (без учета остаточных аберраций и допусков на ошибки изготовления).
В линейной мере объектив имеет предел разрешения
д = 0.55*f’/D (мкм), (5)
где f’ — фокусное расстояние, а D — диаметр объектива.
То есть из-за дифракции на приемнике невозможно разрешить детали отстоящие друг от друга на расстояние меньшее, чем д, если середина спектрального диапазона инструмента приходится на волну с длиной λo = 0.55 мкм. В общем случае д = λo*f/D
Относительное отверстие и фокусное расстояние
Относительное отверстие, которое представляют обычно в виде дроби 1:k — это для объективов отношение диаметра входной апертуры (зрачка) к заднему фокусному расстоянию: 1/k = D/f’, где k еще называют диафрагменным числом (диафрагмой) или относительным фокусным расстоянием k = f’/D. Чем относительное отверстие объектива больше, тем более яркие изображения он строит (поэтому светосила объектива пропорциональна квадрату его относительного отверстия) и тем меньшие по линейному размеру детали он может построить в плоскости изображения. Но и тем труднее совладать в нем с остаточными аберрациями. Заметим, что предел разрешения на фотоприемнике у идеального фотообъектива пропорционален его относительному фокусному расстоянию:
д = λ·k, (6)
где λ, мкм — длина волны середины спектрального диапазона (для визуальных и бытовых фотографических приборов принимают λ = 0.546 мкм), k — относительное фокусное расстояние (с учетом всех использованных экстендеров/редьюсеров и проч.).
Поле зрения/изображения
Поле — максимальный по размеру предмет или его изображение, которые пропускает оптических прибор характеризуется обычно линейной 2Y (2Y’) или угловой 2W (2W’) величиной. Для «удаленного» предмета (как он представляется объективу телескопа или фотоаппарата) 2W и изображения (которое, например, создается окуляром телескопа или лупой) 2W’ поле измеряют в угловой мере — это удвоенный угол между осью оптического прибора и направлением на границу поля зрения, измеренный из центра входного или соответственно выходного зрачка. Для «ближнего» предмета (как он представляется объективу микроскопа или лупе) 2Y или изображения (как у фотообъектива) 2Y’ поле измеряют в линейной мере (в мм) — это удвоенное расстояние от оси прибора до дальней точки кадра.
Как входное, так и выходное поле зрения ограничивается единственной полевой диафрагмой, расположенной на предмете или изображении (возможно промежуточном) или совокупностью виньетирующих диафрагмами (элементы конструкции трубы, оправы оптических элементов, их края). Полевая диафрагма располагается в плоскости изображения и формирует резкую границу кадра (поля зрения), а виньетирующие диафрагмы (не сопряженные оптически с предметом/изображением) — нерезкую. Довольно часто узлы сложных оптических приборов наследуют полевую диафрагму у других узлов. Например, объектив телескопа обычно не имеет собственной полевой диафрагмы (хотя может иметь немало виньетирующих, предназначенных, например, для светозащиты), а «использует» полевую диафрагму окуляра. Поэтому поле зрения телескопа (до известных пределов) определяется окуляром, но может быть ограничено виньетированием на конструкциях объектива (включая размеры фокусера, диагонального зеркала и т.д.).
Значение входного (видимого, TFOV — true field of view) поля зрения телескопа можно рассчитать следующим образом:
2W = 2·arctg(Y’/f’)
или с хорошим приближением:
2W, градусы = 57.3·2Y’/f’об = 2W’ок/Г, (7)
2W, угл.минуты = 60·2Wгр = 3444·2Y’/f’об = 60·2W’ок/Г, (8)
где
2Y’, мм — диаметр полевой диафрагмы окуляра (уменьшенное на кратность линзы Барлоу, если она использовалась) или диагонали кадра на фотоприемнике;
f’об, мм — фокусное расстояние объектива;
2W’ок, градусы — угловое поле зрения окуляра;
Г — увеличение телескопа.
Значение выходного поля зрения телескопа (AFOV — apperant field of view) или углового поля зрения окуляра (при нулевой угловой дисторсии):
2W’, градусы = 57.3·2Y’/f’ок = 2W’ок·Г, (9)
где f’ок, мм — фокусное расстояние окуляра.
Часто для определения видимого поля зрения 2W телескопа используют прием «остановки часовика». Измеряют время t в секундах, за которое достаточно яркая звезда пересечет поле зрения по диаметру от одного края до другого, при остановленном часовом механизме. Тогда поле зрения в угловых минутах определяется следующим образом
2W = t·cos(б)/4, (10)
где б — склонение звезды (для звезд у небесного экватора где б = 0 и cos(б) = 1 угловое поле зрения определяется проще: 2W = t/4).
Увеличение
Увеличение Г — характеризует соотношение размеров изображения и сопряженного с ним объекта.
Для телескопа, бинокля или подзорной трубы это самая важная характеристика — отношение малого угла dw’, под которым глаз видит изображение объекта, к углу dw под которым этот объект виден объективу телескопа: Г = dw’/dw. Для небольших углов полей зрения, характерных для телескопа, более-менее верны (если не вдаваться в детали) следующие общеизвестные соотношения, следующие из этого определения увеличения:
Г = f’об/f’ок ≃ D/D’ ≃ 2W’/2W, (11)
где 2W’ — поле зрения окуляра (или угловой размер наблюдаемого изображения), 2W — поле зрения объектива (или угловой размер наблюдаемого объекта), D — диаметр входной апертуры (входного зрачка) телескопа, D’ — диаметр выходного зрачка телескопа, f’об — фокусное расстояние объектива, f’ок — фокусное расстояние окуляра (если использована линза Барлоу следует домножить на ее заявленную кратность). Увеличение телескопа численно равное D/6-D/7 (D — в мм) принято называть ночным равнозрачковым (выходной зрачок телескопа примерно равен зрачку наблюдателя ночью), 1.5·D — разрешающим (дальнейший рост увеличения не увеличивает детализацию изображения, но приводит к падению яркости).
Для проекционных систем, микро- и макрообъективов увеличение это отношение линейных размеров малого фрагмента изображения dy’, к размеру этого же фрагмента на объекте dy: Г = dy’/dy. Такое увеличение еще называют поперечным увеличением, поскольку это отношение размеров предмета/изображения поперек оптической оси прибора. Стоит обратить внимание на то, оптический прибор (как, к примеру, большинство фотообъективов) может уменьшать размер изображения по сравнению с оригинальным размером объекта (иначе как бы фотографируемые люди поместились на кадр 24х35 мм ), в этом случае оптики продолжают говорить об увеличении, но значение Г при этом меньше единицы. При оборачивании изображения (вверх ногами) величина увеличения Г отрицательная. Для расчета поперечного увеличения верны следующие формулы:
Г = z/f = f’/z’ = a’/a = y’/y, (12)
где z — расстояние от предмета до переднего фокуса изображающей оптической системы, f и f’ — переднее и заднее фокусное расстояния (для объектива в воздухе они равны между собой), z’ — расстояние от заднего фокуса до плоскости изображения, a — передний отрезок (от предмета до передней главной плоскости объектива), a’ — задний отрезок (расстояние от объектива — точнее его задней главной плоскости — до изображения).
Назад к оглавлению статей
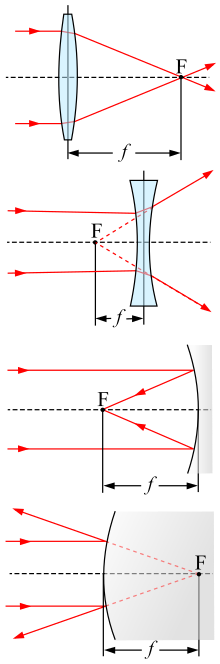
«Заднее фокусное расстояние» перенаправляется сюда. Для получения информации о расстоянии от объектива до пленки в камере см. Фокусное расстояние фланца .
Фокусная точка F и фокусное расстояние f положительной (выпуклой) линзы, отрицательной (вогнутой) линзы, вогнутого зеркала и выпуклого зеркала.
Фокусное из оптической системы является мерой того , насколько сильно система сходится или расходится зажигать ; это обратное из системы оптической мощности . Положительное фокусное расстояние указывает на то, что система собирает свет, а отрицательное фокусное расстояние указывает на то, что система рассеивает свет. Система с меньшим фокусным расстоянием изгибает лучи более резко, фокусируя их на более коротком расстоянии или быстрее рассеивая. Для особого случая тонкой линзы в воздухе положительное фокусное расстояние — это расстояние, на котором первоначально коллимированные (параллельные) лучи попадают в фокус , или, альтернативно, отрицательное фокусное расстояние указывает, как далеко перед линзой должен находиться точечный источник. располагаться так, чтобы формировать коллимированный пучок. Для более общих оптических систем фокусное расстояние не имеет интуитивного значения; это просто величина, обратная оптической мощности системы.
В большинстве фотографий и во всей телескопии , где объект находится практически бесконечно далеко, большее фокусное расстояние (меньшая оптическая сила) приводит к большему увеличению и более узкому углу обзора ; и наоборот, меньшее фокусное расстояние или более высокая оптическая сила связаны с меньшим увеличением и более широким углом зрения. С другой стороны, в таких приложениях, как микроскопия, в которых увеличение достигается за счет приближения объекта к объективу, более короткое фокусное расстояние (более высокая оптическая сила) приводит к большему увеличению, поскольку объект можно приблизить к центру проецирования.
Приближение тонкой линзы
Для тонкой линзы в воздухе фокусное расстояние — это расстояние от центра линзы до основных фокусов (или фокусных точек ) линзы. Для собирающей линзы (например, выпуклой линзы ) фокусное расстояние положительно и представляет собой расстояние, на котором луч коллимированного света будет сфокусирован в единственное пятно. Для расходящейся линзы (например, вогнутой линзы ) фокусное расстояние отрицательно и представляет собой расстояние до точки, от которой коллимированный луч кажется расходящимся после прохождения через линзу.
Когда линза используется для формирования изображения некоторого объекта, расстояние от объекта до линзы u , расстояние от линзы до изображения v и фокусное расстояние f связаны соотношением
Фокусное расстояние тонкой выпуклой линзы можно легко измерить, используя ее для формирования изображения удаленного источника света на экране. Объектив перемещается до тех пор, пока на экране не сформируется резкое изображение. В таком случае1/ты пренебрежимо мало, и фокусное расстояние тогда определяется как
Определить фокусное расстояние вогнутой линзы несколько сложнее. Фокусным расстоянием такой линзы считается точка, в которой распространяющиеся лучи света встретились бы перед линзой, если бы линзы не было. Во время такого теста изображение не формируется, и фокусное расстояние необходимо определять, пропуская свет (например, свет лазерного луча) через линзу, исследуя, насколько этот свет рассеивается / изгибается, и следуя за лучом света. назад к фокусной точке объектива.
Общие оптические системы
Для толстой линзы (имеющей значительную толщину) или системы формирования изображения, состоящей из нескольких линз или зеркал (например, фотографического объектива или телескопа ), фокусное расстояние часто называют эффективным фокусным расстоянием (EFL), чтобы отличить его от других часто используемых параметров:
- Переднее фокусное расстояние (лит) или передние фокусное расстояние (П) ( ы Р ) расстояние от передней фокальной точки системы (F) до вершины на первую оптическую поверхности (S 1 ).
- Заднее фокусное расстояние (BFL) или заднее фокусное расстояние (BFD) ( s ′ F ′ ) — это расстояние от вершины последней оптической поверхности системы (S 2 ) до задней фокусной точки (F ′).
Для оптической системы в воздухе эффективное фокусное расстояние ( f и f ‘ ) дает расстояние от передней и задней главных плоскостей (H и H’) до соответствующих фокальных точек (F и F ‘). Если окружающая среда не воздух, то расстояние умножается на показатель преломления среды ( n — показатель преломления вещества, из которого сделана сама линза; n 1 — показатель преломления любой среды перед линзой. линзы; n 2 — это линза любой среды за ней). Некоторые авторы называют эти расстояния передними / задними фокусными расстояниями , отличая их от передних / задних фокусных расстояний , определенных выше.
Как правило, фокусное расстояние или EFL — это значение, которое описывает способность оптической системы фокусировать свет, и значение, используемое для расчета увеличения системы. Остальные параметры используются при определении , где изображение будет сформировано для данной позиции объекта.
Для случая линзы толщиной d в воздухе ( n 1 = n 2 = 1 ) и поверхностей с радиусами кривизны R 1 и R 2 эффективное фокусное расстояние f определяется уравнением Линсмейкера :
где n — показатель преломления линзовой среды. Количество1/ж также известен как оптическая сила линзы.
Соответствующее переднее фокусное расстояние:
и заднее фокусное расстояние:
В используемом здесь знаковом соглашении значение R 1 будет положительным, если первая поверхность линзы выпуклая, и отрицательным, если она вогнутая. Значение R 2 отрицательно, если вторая поверхность выпуклая, и положительно, если вогнутая. Обратите внимание, что соглашения о знаках различаются у разных авторов, что приводит к разным формам этих уравнений в зависимости от используемого соглашения.
Для сферически изогнутого зеркала в воздухе величина фокусного расстояния равна радиусу кривизны зеркала, деленному на два. Фокусное расстояние положительное для вогнутого зеркала и отрицательное для выпуклого зеркала . В знаковом соглашении, используемом в оптической конструкции, вогнутое зеркало имеет отрицательный радиус кривизны, поэтому
где R — радиус кривизны поверхности зеркала.
См. Радиус кривизны (оптика) для получения дополнительной информации о знаках радиуса кривизны, используемых здесь.
В фотографии
Объектив 28 мм
Объектив 50 мм
Объектив 70 мм
Объектив 210 мм
Пример того, как выбор объектива влияет на угол обзора. Фотографии выше были сделаны 35-мм камерой на фиксированном расстоянии от объекта.
Красным цветом показаны изображения черных букв в тонкой выпуклой линзе с фокусным расстоянием f . Выбранные лучи показаны буквами E , I и K синим, зеленым и оранжевым цветом соответственно. Обратите внимание, что E (на 2 f ) имеет реальное и перевернутое изображение равного размера; I (в точке f ) имеет изображение на бесконечности; и K (приж/2) имеет двойное, виртуальное и вертикальное изображение.
В этом компьютерном моделировании настройка поля зрения (путем изменения фокусного расстояния) при сохранении объекта в кадре (путем соответствующего изменения положения камеры) приводит к сильно различающимся изображениям. На фокусных расстояниях, приближающихся к бесконечности (0 градусов поля зрения), лучи света почти параллельны друг другу, в результате чего объект выглядит «сплющенным». На малых фокусных расстояниях (большее поле зрения) объект кажется «укороченным».
Фокусные расстояния объектива камеры обычно указываются в миллиметрах (мм), но некоторые старые объективы имеют маркировку в сантиметрах (см) или дюймах.
Фокусное расстояние ( f ) и поле зрения (FOV) объектива обратно пропорциональны. Для стандартного прямолинейного объектива FOV = 2 арктангенса. Икс/2 ж, где x — диагональ пленки.
Когда фотографический объектив установлен на «бесконечность», его задняя узловая точка отделена от датчика или пленки в фокальной плоскости фокусным расстоянием объектива. Объекты, расположенные далеко от камеры, затем создают четкие изображения на датчике или пленке, которые также находятся в плоскости изображения.
Чтобы визуализировать более близкие объекты в резком фокусе, объектив необходимо отрегулировать так, чтобы увеличить расстояние между задней узловой точкой и пленкой, чтобы пленка находилась в плоскости изображения. Фокусное расстояние ( f ), расстояние от передней узловой точки до фотографируемого объекта ( s 1 ) и расстояние от задней узловой точки до плоскости изображения ( s 2 ) связаны следующим образом:
В качестве сек 1 уменьшается, ˙s 2 должна быть увеличена. Например, рассмотрим обычный объектив для 35-мм камеры с фокусным расстоянием f = 50 мм. Для фокусировки удаленного объекта ( s 1 ≈ ∞) задняя узловая точка линзы должна находиться на расстоянии s 2 = 50 мм от плоскости изображения. Чтобы сфокусировать объект на расстоянии 1 м ( s 1 = 1000 мм), линзу необходимо отодвинуть на 2,6 мм от плоскости изображения до s 2 = 52,6 мм.
Фокусное расстояние объектива определяет увеличение, при котором он отображает удаленные объекты. Он равен расстоянию между плоскостью изображения и точечным отверстием, которое отображает удаленные объекты того же размера, что и рассматриваемая линза. Для прямолинейных линз (то есть без искажения изображения ) отображение удаленных объектов хорошо моделируется как модель камеры-обскуры . Эта модель приводит к простой геометрической модели, которую фотографы используют для вычисления угла обзора камеры; в этом случае угол обзора зависит только от отношения фокусного расстояния к размеру пленки . В общем, угол обзора зависит также от искажения.
Объектив с фокусным расстоянием, примерно равным размеру диагонали пленки или формата сенсора, известен как нормальный объектив ; его угол обзора аналогичен углу, который образует достаточно крупный отпечаток, просматриваемый на типичном расстоянии просмотра диагонали отпечатка, что, таким образом, дает нормальную перспективу при просмотре отпечатка; этот угол обзора составляет около 53 градусов по диагонали. Для полнокадровых фотоаппаратов формата 35 мм диагональ составляет 43 мм, а типичный «нормальный» объектив имеет фокусное расстояние 50 мм. Объектив с фокусным расстоянием меньше обычного часто называют широкоугольным объективом (обычно 35 мм и меньше для камер формата 35 мм), тогда как объектив, который значительно длиннее обычного, может называться телеобъективом ( обычно 85 мм и более для камер формата 35 мм). Технически линзы с длинным фокусным расстоянием являются «телеобъективами» только в том случае, если фокусное расстояние больше, чем физическое расстояние объектива, но этот термин часто используется для описания любого объектива с длинным фокусным расстоянием.
Из-за популярности стандарта 35 мм комбинации камера-объектив часто описываются в терминах их фокусного расстояния , эквивалентного 35 мм , то есть фокусного расстояния объектива с таким же углом зрения или полем зрения. , если используется с полнокадровой 35-мм камерой. Использование фокусного расстояния, эквивалентного 35 мм, особенно распространено в цифровых камерах , в которых часто используются датчики размером меньше 35 мм пленки, и поэтому для достижения заданного угла обзора требуются соответственно более короткие фокусные расстояния с коэффициентом, известным как кроп-фактор .
Смотрите также
- Глубина резкости
- Диоптрий
- f-число или фокусное отношение