Мы с вами продолжаем рассматривать прямолинейное
равноускоренное движение тела. Теперь давайте рассмотрим, как определить
проекцию вектора перемещения тела при его равноускоренном движении без
начальной скорости. В этом случае уравнение проекции перемещения будет иметь
вид:
Для простоты дальнейших рассуждений будем считать, что
направление векторов перемещения и ускорения тела совпадают. Тогда записанное
нами уравнение мы можем переписать, подставив в него вместо проекций векторов
ускорения и перемещения их модули:
Так как ускорение тела является величиной постоянной, то из
формулы следует, что при прямолинейном равноускоренном движении модуль
вектора перемещения прямо пропорционален квадрату времени, в течение которого
это перемещение совершено.
Например, если тело за некоторый промежуток времени t1 совершило
перемещение s1,
то за вдвое большее время оно совершит в четыре раза большее перемещение. Если
промежуток времени увеличится в 3 раза, по сравнению с первоначальным, то
перемещение тела увеличится уже в 9 раз, по сравнению с первоначальным. Логично
предположить, что в случае увеличения промежутка времени в k раз, перемещение увеличится в k2 раз. Только
помним, что число k
должно быть натуральным:
Данную закономерность можно представить графически в виде
последовательных отрезков перемещений:
Или с помощью графика скорости для равноускоренного движения
без начальной скорости:
Из рисунков хорошо видно, что в случае увеличения
промежутков времени, отсчитываемых от начала движения, в целое число раз,
модули соответствующих векторов перемещений возрастают как ряд квадратов
последовательных натуральных чисел:
Теперь давайте найдём отношения модулей перемещений,
проходимых телом за равные последовательные промежутки времени. Получим, что модули
векторов перемещений, совершаемых телом за равные последовательные промежутки
времени при прямолинейном равноускоренном движении без начальной скорости,
относятся как ряд нечётных чисел:
Полученными закономерностями обладает только равноускоренное
движение. Поэтому ими можно пользоваться в случае, когда требуется определить,
как движется тело — с ускорением или без него.
Например, пусть нам требуется определить, является ли
движение гусеницы равноускоренным, если она за первые 10 секунд движения
переместилась на 5 сантиметров, за вторые 10 секунд — на 15 сантиметров, а за
третьи 10 секунд — на 25 сантиметров.
Для этого найдём отношения перемещений, совершённых за второй
и третий промежутки времени, к перемещению гусеницы на первом отрезке времени:
Таким образом видим, что полученные отношения представляют
собой последовательный ряд нечётных чисел. Значит, движение гусеницы было
равноускоренным.
Закрепление материала. В течение восьми равных
промежутков времени от начала движения тело, двигаясь равноускорено,
переместилось на 160 метров. Какой путь прошло это тело в течение двух первых
таких же промежутков времени?
- Подробности
- Обновлено 06.03.2019 16:34
- Просмотров: 350
1. По каким формулам рассчитываются проекция и модуль вектора перемещения тела при его равноускоренном движении из состояния покоя?
Исходная расчетная формула проекции вектора перемещения тела, движущегося равноускоренно:
Проекция вектора перемещения тела, движущегося равноускоренно, если его начальная скорость v0 равна нулю:
Модуль вектора перемещения при прямолинейном равноускоренном движении без начальной скорости прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено:
2. Каковы закономерности равноускоренного движения без начальной скорости ?
а)
ОА : ОВ : ОС : OD : 0E = 1 : 4 : 9 : 16 : 25
т. е. при увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t1, модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел.
б)
OA : AB : BC : CD : DE = 1 : 3 : 5 : 7 : 9
т. е. модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени (каждый из которых равен t1), относятся как ряд последовательных нечётных чисел.
3. Во сколько раз увеличится модуль вектора перемещения тела при увеличении времени его движения из состояния покоя в n раз?
При увеличении в n раз времени движения, отсчитываемого от момента начала движения, перемещение увеличивается в n2 раз.
4. Как относятся друг к другу модули векторов перемещений тела, движущегося равноускоренно из состояния покоя, при увеличении времени его движения в целой число раз по сравнению с t1?
При увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t1, модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел.
5. Как относятся друг к другу модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, если это тело движется равноускоренно из состояния покоя?
Модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, относятся как ряд последовательных нечётных чисел.
6. С какой целью можно использовать эти закономерности?
ОА : ОВ : ОС : OD : ОЕ = 1 : 4 : 9 : 16 : 25
ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9
Вышеуказанные закономерности присущи только равноускоренному движению.
Ими можно пользоваться, если необходимо определить, является движение равноускоренным или нет.
Например:
Задача.
Определим, было ли равноускоренным движение улитки, которая:
—
за первые 20 с движения переместилась на 0,5 см,
—
за вторые 20 с — на 1,5 см,
—
за третьи 20 с — на 2,5 см.
Для этого найдём, во сколько раз перемещения, совершённые за второй и третий промежутки времени, больше, чем за первый:
Значит, 0,5 см : 1,5 см : 2,5 см = 1 : 3 : 5.
Поскольку эти отношения представляют собой ряд последовательных нечётных чисел, то движение тела было равноускоренным.
Равноускоренный характер движения был выявлен на основании закономерности:
ОА : АВ : ВС : CD : DE = 1 : 3 : 5 : 7 : 9
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Прямолинейное равноускоренное движение
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в XVI веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении без изменения направления скорости модуль перемещения совпадает по своему значению с пройденным путем. Формула выглядит следующим образом:
где – это ускорение.
Примеры равноускоренного движения без начальной скорости
Равноускоренное движение без начальной скорости – важный особый случай равноускоренного движения. Рассмотрим примеры:
1. Свободное падение без начальной скорости. Примером такого движения может быть падение сосульки в конце зимы (рис. 1).
Рис. 1. Падение сосульки
В тот момент, когда сосулька отрывается от крыши, ее начальная скорость равна нулю, после чего она движется равноускоренно, ведь свободное падение – это равноускоренное движение.
2. Старт любого движения. Например, автомобиль трогается с места и разгоняется (рис. 2).
Рис. 2. Старт движения
Когда мы говорим, что время набора скорости 100 км/ч у автомобиля той или иной марки, например, 6 с., чаще всего мы говорим о движении равноускоренном без начальной скорости. Аналогично когда мы говорим о старте ракеты и т. д.
3. Особую актуальность равноускоренное движение имеет для разработчиков оружия. Ведь вылет любого снаряда или пули – это движение без начальной скорости, а во время движения в стволе пуля (снаряд) движется равноускоренно. Рассмотрим пример.
Длина автомата Калашникова – . Пуля в стволе автомата движется с ускорением
. С какой скоростью пуля будет вылетать из ствола?
Рис. 3. Иллюстрация к задаче
Для нахождения скорости вылета пули из ствола автомата воспользуемся выражением для перемещения при прямолинейном равноускоренном движении, если неизвестно время:
Движение осуществляется без начальной скорости, а значит, , тогда
.
Получим следующее выражение для нахождения скорости вылета пули из ствола:
Решение задачи записываем следующим образом с учетом единиц измерения в СИ:
|
Дано:
|
СИ:
|
Решение:
|
|
|
Ответ: |
Равноускоренное движение без начальной скорости часто встречается и в природе, и в технике. Более того, умение работать с таким движением позволяет решать обратные задачи, когда начальная скорость существует, а конечная равна нулю.
Случай равномерного движения
Если , то уравнение, приведенное выше, превратится в уравнение:
Это уравнение дает возможность найти пройденный путь равномерного движения. в данном случае является проекцией вектора перемещения. Ее можно определить как разность координат:
. Если подставить это выражение в формулу, то получим зависимость координаты от времени:
Случай движения без начальной скорости
Рассмотрим ситуацию, когда – начальная скорость равна нулю. Это значит, что движение начинается из состояния покоя. Тело покоилось, затем начинает приобретать и увеличивать скорость. Движение из состояния покоя будет записываться без начальной скорости:
Если S (проекцию перемещения) обозначить как разность начальной и конечной координаты (), то получится уравнение движения, которое дает возможность определить координату тела для любого момента времени:
Проекция ускорения может быть, как отрицательной, так и положительной, поэтому можно говорить о координате тела, которая может как увеличиваться, так и уменьшаться.
График зависимости скорости от времени 
Так как равноускоренное движение без начальной скорости является особым случаем равноускоренного движения, рассмотрим график зависимости проекции скорости от времени для такого движения.
На рис. 4 представлен график зависимости проекции скорости от времени для равноускоренного движения без начальной скорости (график начинается в начале координат).
График устремлен вверх. Это говорит о том, что проекция ускорения положительна
Рис. 4. График зависимости проекции скорости от времени при равноускоренном движении без начальной скорости
Используя график, можно определить проекцию перемещения тела или пройденный путь. Для этого необходимо посчитать площадь фигуры, ограниченной графиком, координатными осями и перпендикуляром, опущенным на ось времени. То есть необходимо найти площадь прямоугольного треугольника (половина произведения катетов)
где – конечная скорость при равноускоренном движении без начальной скорости:
тогда:
На рис. 5 представлен график зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости.
Рис. 5. График зависимости проекции перемещения от времени двух тел для равноускоренного движения без начальной скорости
Начальная скорость обоих тел равна нулю, так как вершина параболы совпадает с началом координат:
У первого тела проекция ускорения положительна , у второго – отрицательна
. Причем у первого тела проекция ускорения тела больше, так как перемещение у него осуществляется быстрее.
Пропорциональность пути квадрату времени
– пройденный путь (с точностью до знака), он пропорционален
, т. е. квадрату времени. Если рассматривать равные промежутки времени –
,
,
, то можно заметить следующие соотношения:
Если продолжить вычисления, закономерность сохранится. Пройденные расстояния увеличиваются пропорционально квадрату увеличения промежутков времени.
Например, если , то пройденный путь будет пропорционален
. Если
, пройденный путь будет пропорционален
и т. д. Расстояние будет расти пропорционально квадрату этих промежутков времени (рис. 6).
Рис. 6. Пропорциональность пути квадрату времени
Перемещения за последовательные (равные) промежутки времени
Если за единицу времени выбираем некий промежуток, то полные расстояния, пройденные телом за последующие равные промежутки времени, будут относиться как квадраты целых чисел.
Иными словами, перемещения, совершенные телом за каждую последующую секунду, будут относиться как нечетные числа:
Рис. 7. Перемещения за каждую секунду относятся как нечетные числа
Исследованные два очень важных заключения свойственны только прямолинейному равноускоренному движению без начальной скорости.
Рассмотренные закономерности на примере задачи
Задача. Автомобиль начинает двигаться от остановки, т. е. из состояния покоя, и за четвертую секунду своего движения проходит 7 м. Определите ускорение тела и мгновенную скорость через 6 с после начала движения (рис. 8).
Рис. 8. Иллюстрация к задаче
Решение: автомобиль начинает движение из состояния покоя, следовательно, путь, который проходит автомобиль, рассчитывается по формуле: . Мгновенная скорость определяется как
.
– расстояние, которое автомобиль прошел за четвертую секунду своего движения. Его можно выразить как разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с (рис. 9).
Рис. 9. Разность полного пути, пройденного телом за 4 с, и пути, пройденного телом за 3 с
Решив уравнение, получаем ускорение .
Чтобы определить мгновенную скорость, т. е. скорость в конце шестой секунды, следует ускорение умножить на время, т. е. на 6 с, во время которых тело которое продолжало двигаться.
Заключение
Уравнения, которые сегодня мы использовали в уроке, впервые были исследованы Галилео Галилеем. На следующем уроке мы рассмотрим, как именно были проведены эти опыты.
Список литературы
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «phscs.ru» (Источник)
- Интернет-портал «fizikaklass.ru» (Источник)
- Интернет-портал «sernam.ru» (Источник)
Домашнее задание
- Запишите формулу, которая используется для определения перемещения тела при его равноускоренном движении из состояния покоя.
- Если увеличить время движения тела из состояния покоя в 5 раз, во сколько увеличится модуль вектора перемещения тела?
- Автобус начинает свое движение от остановки и за 5 с своего движения проходит 15 м. Определите ускорение автобуса через 8 с после начала движения.
Равномерно ускоренное движение без начальной скорости
Перемещение выраженное через скорость и время
Тело начинает двигаться равноускоренно из состояния покоя.
|
На графике скорости перемещение равно площади треугольника
[s = frac{ut}{2}] Здесь: |
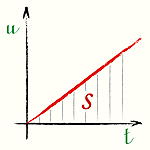 График скорости — Равномерно ускоренное движение без начальной скорости |
Скорость выраженная через ускорение и время
|
Поскольку движение начинается из состояния покоя, то изменение скорости равно величине скорости, достигнутой к моменту времени t, и скорость вычисляется по следующей формуле:
[u = at] |
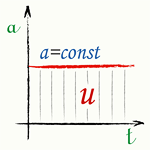 График ускорения — Равномерно ускоренное движение без начальной скорости |
Перемещение выраженное через ускорение и время
|
Из формул (1) и (2) получается следующая формула пройденного пути:
[s = frac{at^2}{2}] Здесь: |
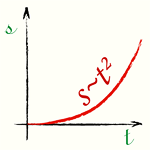 График перемещения — Равномерно ускоренное движение без начальной скорости |
Равномерно ускоренное движение без начальной скорости |
стр. 399 |
|---|
Тема: Перемещение тела при прямолинейном равноускоренном движении
без начальной скорости.
Цель: определить условия, позволяющие находить перемещение тела при прямолинейном равноускоренном движении без начальной скорости.
Ход урока
Основной материал.
Закономерности, присущие прямолинейному равноускоренному движению
без начальной скорости.
-
=
t +
; если
= 0, то
=
,а S =
модуль вектора перемещения прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено.
-
Если за время t,
=
, за время
=2
,
=
, за время
=3
,
=
, отношение модулей перемещений равно отношению квадратов последовательных натуральных чисел:
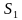
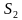

(Арабские цифры используются около символов величин, характеризующих движение от его начала.)
-
Модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, относятся как ряд последовательных нечетных чисел
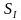

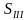
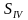
(Римские цифры указывают на то, что данная физическая величина не связана с началом движения. Например, 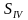
-
При прямолинейном равноускоренном движении без начальной скорости модуль перемещения, совершенного телом за первую секунду, численно равен половине модуля ускорения.
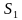
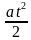

= 1
;
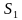
·1
=
.
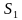
Эти закономерности используются для доказательства равноускоренного характера движения.
Решение задач на нахождение перемещения тела
при прямолинейном равноускоренном движении без начальной скорости.
Задача 1
О пределить среднюю скорость движения тела, если первую половину пути оно прошло со скоростью 10 м/с, а вторую — со скоростью 15 м/с.
Задача 2
Н айти перемещение, пройденный телом в равноускоренном движении из состояния покоя за время 1 мин, если ускорение равно 0,2 м/с2.
Задача 3
В равноускоренном движении из состояния покоя тело прошло путь 100 м. Определить время движения, если ускорение было равно 0,5 м/с2.
Задача 4
Тело движется прямолинейно с ускорением 0,6 м/с2. Какой путь оно пройдет в первую и десятую секунду, если начальная скорость была равна нулю?
Задача 5
Поезд в метро, двигаясь прямолинейно и равноускоренно из состояния покоя, за четвертую секунду прошел 4,34 м.
Определите:
а) модуль перемещения, совершенного поездом за первую секунду;
б) ускорение движения и скорость, которую он приобрел к концу шестой секунды движения.
Карточка № 1
-
Тело, двигаясь без начальной скорости, прошло за первую секунду 1 м, за вторую — 2 м, за третью — 3 м, за четвертую — 4 м и т. д. Является ли такое движение равноускоренным?
-
Автомобиль трогается с места с ускорением 2 м/с2. Каково его перемещение за 5 с? Какую скорость он наберет за это время?
Карточка № 2
-
Стартующая ракета за 10 с набрала скорость 100 м/с. С каким ускорением двигалась ракета? Каково ее перемещение за это время?
-
При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определите путь тела за седьмую секунду.
Домашнее задание: §8; упр. 8
Решение задач на чтение и составление
уравнения прямолинейного равноускоренного движения.
-
Прямолинейное движение тела описывается уравнением движения: х = 10 — 8t +
.
Написать уравнение скорости движения. Какое перемещение совершило тело за первые 2 с движения? Через какое время от начала движения тела его координата будет равна нулю?
-
На рисунке показаны положения двух человек в момент времени t = 0, а также их начальные скорости и ускорения.
Записать уравнения движения, построить графики проекции скоростей двух тел.
-
Уравнение скорости имеет вид
= 2 + 5t. Найдите перемещение тела за пятую секунду.















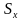 =
= 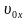 t +
t + 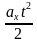 ; если
; если  , за время
, за время  =2
=2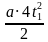 , за время
, за время  =3
=3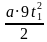 , отношение модулей перемещений равно отношению квадратов последовательных натуральных чисел:
, отношение модулей перемещений равно отношению квадратов последовательных натуральных чисел: