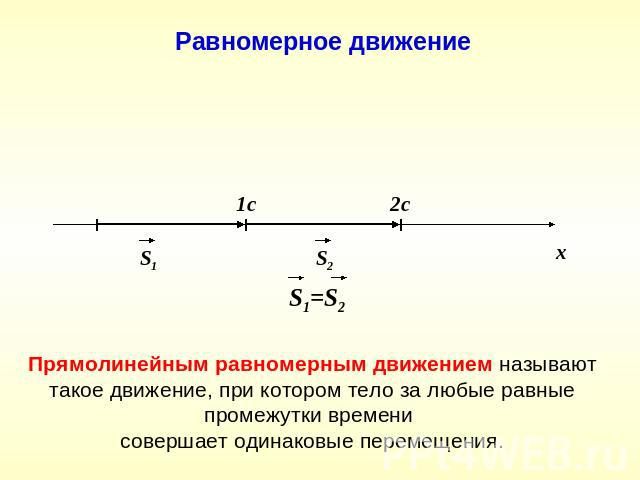
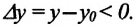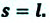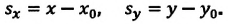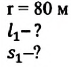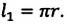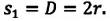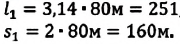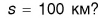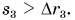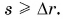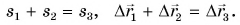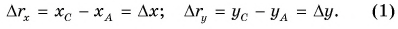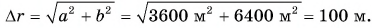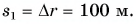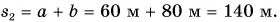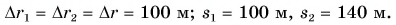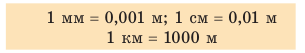Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения.
v→=s→t.
Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s→=v→⋅t.
О направлении векторов этих величин относительно друг друга можно судить, в частности, по уравнениям, записанным в векторной форме.
Проекция перемещения на ось (OX) рассчитывается по формуле
sx=vxt
, где (upsilon_x) — проекция скорости на ось (OX) принимает положительное значение, если направление перемещения совпадает с направлением оси (OX); принимает отрицательное значение, если перемещение противоположно направлено относительно оси (OX).
Если при решении задач направление движения не влияет на смысл условия и ход решения задачи, то направление векторных величин можно не учитывать. Тогда говорят о модулях величин, то есть их размере без учёта направления: (|vec{s}|=|vec{upsilon}|cdot t) можно заменить на s=vt.
При прямолинейном равномерном движении модуль перемещения равен пройденному пути: (|vec{s}|=s), если направление скорости совпадает с направлением вектора перемещения.
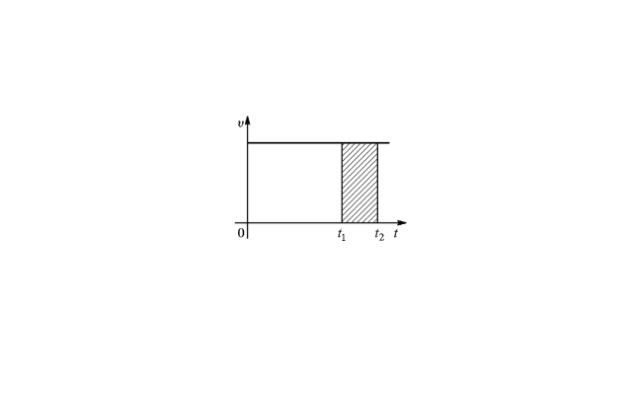
На рисунке представлена зависимость (v(t)) для равномерного движения.
Формула для расчета модуля перемещения: s=v1⋅t1.
Однако произведение v1⋅t1, т.е. скорости на промежуток времени, численно равно площади (S) закрашенной фигуры (в данном случае прямоугольника).
Это наблюдение позволяет сделать вывод; что при прямолинейном равномерном движении модуль перемещения численно равен площади прямоугольника, которые образуется между графиком скорости и осью времени. При этом необходимо учитывать моменты времени: начало наблюдения за объектом и конец наблюдения. В данном случае начало наблюдения соответствует точке (O,) а конец наблюдения — точке t1.
Можно говорить о равенстве пройденного пути и площади под графиком скорости.
В процессе механического движения положение тела в
пространстве меняется с течением времени. До сегодняшнего дня при решении
большинства задач на движение тел, мы использовали понятие «путь». Оно вам
хорошо известно. Напомним, что путь — это длина траектории, пройденной телом
за время наблюдения.
А траектория — это воображаемая линия в пространстве, по
которой движется тело.
Путь чаще всего обозначают малой латинской буквой s, а единицей пути в СИ
является метр.
Путь — это скалярная величина, то есть величина, имеющая
числовое значение, но не имеющая направления.
Положение тела через некоторый промежуток времени можно
определить, зная траекторию движения, начальное положение тела на траектории и
пройденный телом за этот промежуток времени путь. Если же траектория движения
тела неизвестна, то его положение в некоторый момент времени определить нельзя,
поскольку один и тот же путь тело может пройти в разных направлениях. Покажем
это.
Пусть, например, из лыжной базы в 20 километрах к северу от
города вышел лыжник и за 2,5 часа прошёл 20 километров пути. Как определить,
куда он пришёл? Ведь он мог находиться в различных местах, удалённых от лыжной
базы не более чем на 20 километров. Он мог дойти, например, до города. А мог,
пройдя в каком-либо направлении 10 километров, вернуться на базу. В любом
случае путь будет равен 20 километрам, но положение лыжника в пространстве
будет разным.
Поэтому для определения положения лыжника нам необходимо
знать направление его движения и расстояние, пройденное им в этом направлении. Направленный
отрезок прямой, соединяющий начальное положение тела с его конечным положением,
называется перемещением тела.
Таким образом, перемещение — это векторная величина, то есть
имеет направление и числовое значение (модуль).
Обозначается перемещение, как и путь, малой латинской буквой s, только со стрелочкой
над ней. Единицей перемещения в СИ является метр.
Таким образом, если знать начальное положение тела и его
перемещение за некоторый промежуток времени, то можно легко определить
положение тела в конце этого промежутка времени.
— А как складываются или вычитаются между собой пути и как
перемещения?
Так как путь — это величина скалярная, то пройденные пути
складываются и вычитаются арифметически. Например, если известно, что катер
проплыл 10 километров на север. Затем 15 километров на восток и ещё 30
километров на юго-восток, то общий путь, пройденный катером, равен 55
километрам.
Перемещения же складываются и вычитаются по правилам сложения
и вычитания векторов.
Давайте вспомним, как складываются векторы. Итак, если два
вектора направлены одинаково, то их сумма — это вектор того же направления,
имеющий модуль, равный сумме модулей данных двух векторов.
Если же направления векторов противоположны, то их сумма —
это вектор, который направлен так же, как вектор, модуль которого больше. При
этом модуль полученного вектора равен разности модулей слагаемых векторов.
— А как сложить векторы, направленные под углом друг к другу?
Для этого существуют несколько правил. Первое называется правилом
параллелограмма.
Чтобы сложить два вектора по этому правилу, необходимо
параллельным переносом совместить начала слагаемых векторов. Затем построить
параллелограмм, принимая складываемые векторы за его стороны. Суммой векторов
будет являться вектор, совпадающий с большей диагональю параллелограмма.
Второе правило называется правилом треугольника. Чтобы
сложить два вектора по этому правилу, необходимо параллельным переносом
совместить конец одного вектора с началом второго вектора. Вектор, проведённый
из начала вектора а в конец вектора b, и равен их сумме.
Если нам требуется найти сумму нескольких векторов, то необходимо
параллельным переносом совместить векторы так, чтобы каждый следующий вектор
выходил из конца предыдущего. Замыкающий вектор, проведённый из начала первого
вектора в конец последнего, и есть искомая сумма данных векторов. Такой способ
сложения называется правилом многоугольника.
Ну и наконец, если требуется найти разность двух векторов,
необходимо параллельным переносом совместить начала векторов a и b. А затем провести
вектор из конца вычитаемого вектора в конец уменьшаемого вектора.
Вспомнив правила сложения и вычитания векторов, мы можем
утверждать, что общем случае, перемещение не совпадает с траекторией движения
тела. А модуль перемещения — с пройденным путём.
Например, пусть автомобиль отправился из Москвы в
Санкт-Петербург и вернулся обратно. Кратчайший автомобильный маршрут от центра
Москвы до центра Санкт-Петербурга имеет протяжённость 710 километров. Поэтому
путь, который проехал автомобиль, составляет 1420 километров. А вот его
перемещение равно нулю. Поэтому помните, что модуль перемещения и пройденный
путь равны только в том случае, если тело движется по прямолинейной траектории
в одну сторону. Иными словами, путь не может быть меньше модуля
перемещения.
Закрепление материала.
Определите сумму и разность взаимно перпендикулярных векторов
a и b. Найдите модули
векторов суммы их суммы и разности.
В заключении урока давайте посмотрим, зависит ли форма
траектории, путь и перемещение от выбора системы отсчёта. Для этого проделаем
такой опыт. Приложим к диску вертикальную рейку в его середине и раскрутим
диск. Теперь проведём вдоль рейки мелом от центра диска вниз. При таком
движении в системе отсчёта, связанной с Землёй, траекторией мела является
прямая линия. А путь и модуль перемещения мела будут равны.
Однако на диске при этом вычерчивается спираль, которая
показывает траекторию движения того же самого мела в системе отсчёта, связанной
с диском, — и эта траектория является криволинейной.
Или вот ещё один опыт, описанный ещё в книге Галилея «Диалог
о двух системах мира». Суть опыта в следующем. С вершины мачты плывущего
корабля на его палубу падает ядро. В системе отсчёта, связанной с кораблём,
траектория движения ядра — это прямолинейный отрезок. Однако с точки зрения
наблюдателя, стоящего на берегу, ядро имело некоторую начальную горизонтальную
скорость, равную скорости корабля. Поэтому траектория движения ядра
криволинейная.
Таким образом, на этом примере мы видим, что форма
траектории, путь и перемещение тела в различных системах отсчёта различны.
Решая задачи, связанные с движением тел, мы использовали такие величины, как скорость или средняя скорость, время движения и пройденный путь. Но дело в том, что знание пройденного телом пути не всегда дает нам возможность определить конечное положение тела в пространстве.
Поэтому в физике используется специальная векторная величина — перемещение. На данном уроке вы узнаете, чем перемещение отличается от пути и как его найти, если для этого требуется произвести сложение или вычитание нескольких перемещений.
Путь
Вспомним уже знакомые нам определения (рисунок 1).
Путь — это длина траектории, по которой двигалось тело в течение определенного промежутка времени.
Траектория — это воображаемая линия в пространстве, по которой движется тело.
Мы обозначали путь буквами $s$ или иногда $l$. При этом путь всегда был для нас скалярной величиной. То есть эта величина не указывала нам никакое направление, а просто давала нам информацию численного характера — сколько метров прошло тело при его движении.
Зачем же теперь нам понадобилось вводить еще одну величину? Давайте рассмотрим на примере, почему знания пройденного телом пути может быть недостаточно для определения его положения в пространстве в какой-то определенный момент времени.
Итак, пусть нашим рассматриваемым телом (материальной точкой) будет автомобиль. Он выезжает из точки O. За $1 space ч$ он проехал путь, равный $60 space км$. И где же он теперь? На рисунке 2 показаны разные точки (A, B, C, D), где он может оказаться. Длины траекторий OA, OB, OC и OD равны между собой ($l = 60 space км$).
Как вы видите, мы не можем ответить на вопрос, где же находится автомобиль в конце своего движения.
Перемещение
Чтобы избежать неопределенности, показанной выше, мы вводим новую физическую величину — перемещение.
Что называют перемещением тела (материальной точки)?
Перемещение — это вектор, соединяющий начальное положение тела с его последующим положением в пространстве.
Обратите внимание, что перемещение — это векторная величина. То есть она имеет некоторое направление.
Обозначается перемещение той же буквой, что и путь, но со стрелочкой — $vec s$. В СИ модуль перемещения $|vec s|$ измеряется в метрах ($м$).
Как тогда будет выглядеть векторы перемещений для автомобиля, который мы рассматривали ранее? Взгляните на рисунок 3.
- Если бы автомобиль прямолинейно поехал на север — вектор был бы $vec s_{OA}$;
- При прямолинейном движении на юго-восток — вектор $vec s_{OC}$;
- По криволинейной траектории OD — вектор $vec s_{OD}$;
- Движение до точки B и обратно в точку O (по кругу) — вектор перемещения $vec s_{OB}$ будет равен нулю.
Зная начальное положение тела и вектор перемещения, мы можем однозначно определить, где это тело находится.
Сложение путей
Рассмотрим, как мы можем найти суммарный путь, если он складывается из нескольких.
Например, самолет движется на север и пролетает $100 space км$. Затем $150 space км$ на запад и еще $300 space км$ на юго-запад (рисунок 4).
Путь — скалярная величина. Значит, складывать пути мы будем арифметически:
$s = s_1 + s_2 + s_3 = 100 space км + 150 space км + 300 space км = 550 space км$.
Вычитание и сложение перемещений
Если мы рассматриваем подобные операции с перемещениями, то здесь у нас будут действовать правила сложения и вычитания векторов.
Если два вектора $vec a$ и $vec b$ имеют одинаковое направление, то их сумма — это вектор $vec c$ того же направления. Его модуль будет равен сумме модулей двух данных векторов: $|vec c| = |vec a| + |vec b|$ (рисунок 5).
Если направления векторов $vec a$ и $vec b$ противоположны, то их сумма — это вектор $vec c$, одинаковый по направлению с тем вектором, модуль которого больше ($vec a$). Модуль итогового вектора будет равен разности модулей слагаемых векторов: $|vec c| = |vec a| − |vec b|$ (рисунок 6).
Правило параллелограмма
Если векторы расположены под некоторым углом друг к другу, то мы можем использовать правило параллелограмма.
Для этого мы совмещаем начала векторов $vec a$ и $vec b$, которые нужно сложить друг с другом, и достраиваем параллелограмм на их основе (рисунок 7).
Суммой данных векторов является вектор $vec c$, выходящий из точки, в которой расположены начала слагаемых векторов $vec a$ и $vec b$, и совпадающий с большей диагональю параллелограмма.
Правило треугольника
Также при работе с векторами вы можете использовать правило треугольника. Для этого нужно совместить конец одного вектора с началом другого (рисунок 8). Так мы получим вектор $vec c$, равный сумме $vec a$ и $vec b$.
Правило многоугольника
Если нам потребуется найти сумму более, чем двух векторов, то мы используем правило многоугольника.
Например, нам нужно сложить четыре вектора $vec a$, $vec b$, $vec c$ и $vec d$. Для этого мы совмещаем векторы так, чтобы каждый следующий выходил из конца предыдущего (рисунок 9). Затем соединяем начало первого вектора $vec a$ и конец последнего $vec d$ и получаем суммарный вектор $vec e$.
Вычитание векторов
Наконец, если нам потребуется найти разность двух векторов $vec a$ и $vec b$, нужно совместить их начала. Затем мы проводим вектор $vec c$ ($vec c = vec a space − space vec b$) из конца вычитаемого вектора $vec b$ в конец уменьшаемого вектора $vec a$ (рисунок 10).
Упражнения
Упражнение №1
Какую физическую величину определяет водитель автомобиля по счетчику спидометра — пройденный путь или перемещение?
Посмотреть ответ
Скрыть
Ответ:
Счетчик, расположенный под спидометром, по которому смотрят так называемый «пробег» автомобиля называется одометром (рисунок 11). Этот прибор считает количество оборотов колеса. Каждый оборот колеса соответствует определенному пройденному пути, поэтому показания прибора выводятся в километрах.
Соответственно, одометр показывает пройденный автомобилем путь, а не его перемещение.
Упражнение №2
Как должен двигаться автомобиль в течение некоторого промежутка времени, чтобы по спидометру можно было определить модуль перемещения, совершенного автомобилем за этот промежуток времени?
Посмотреть ответ
Скрыть
Ответ:
Автомобиль должен двигаться прямолинейно. Тогда пройденный им путь будет равен модулю перемещения.
Перемещение при прямолинейном равномерном движении

4.7
Средняя оценка: 4.7
Всего получено оценок: 145.
4.7
Средняя оценка: 4.7
Всего получено оценок: 145.
Наиболее простым видом движения является прямолинейное равномерное движение. Рассмотрим перемещение при таком движении.
Формула перемещения
Прямолинейное равномерное движение – это движение с постоянной скоростью $v$, без ускорения ($a=0$).
Модуль вектора перемещения у такого движения прямо пропорционален времени движения $t$:
$$s=vt$$
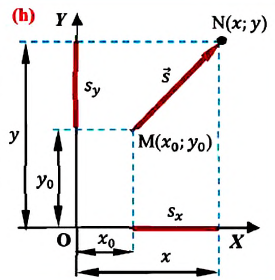
А по определению, вектор перемещения равен разнице между начальной и текущей координатами материальной точки:
$$s=x-x_0$$
Подставляя значение вектора перемещения из одной формулы в другую, можно получить зависимость, описывающую текущую координату материальной точки в зависимости от времени:
$$x-x_0=vt$$
Окончательно имеем:
$$x=x_0+vt$$
Это и есть формула перемещения при прямолинейном равномерном движении.
Эту формулу можно представить и в векторном виде:
$$overrightarrow x=overrightarrow {x_0}+overrightarrow v t$$
Движение на плоскости или в пространстве
При движении по плоскости или в трехмерном пространстве следует использовать векторную форму представленной формулы. Векторы проецируются на оси координат, и дальше проводятся расчеты для каждой координаты вектора перемещения.
Например, если начальная координата на плоскости задана точкой $(1,2)$, скорость задана вектором $(3,4)$, то после проекции на оси абсцисс и ординат получаем две формулы:
- По оси абсцисс: $$x=1+3t$$
- По оси ординат: $$x=2+4t$$
Теперь, подставив время (например, 5с) в эти формулы, получим точку $(16,22)$, которая будет координатами точки перемещения в указанный момент.
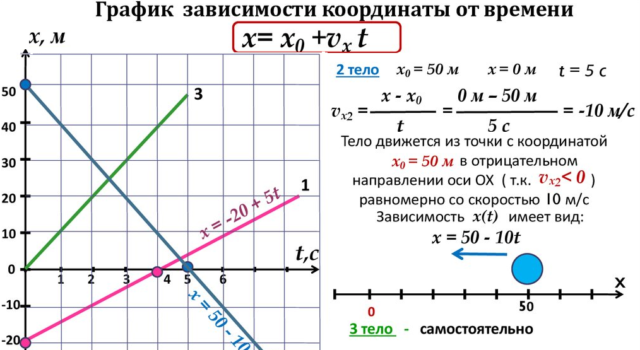
График перемещения
Во многих случаях движение тел удобно представлять в виде графика. По оси абсцисс в этом случае откладывается время в пути, а по оси ординат – значение координаты. Для построения графика используется полученная формула.
Исходя из вида формулы, а также построив несколько различных графиков, можно отметить важные особенности графика перемещения при равномерном прямолинейном движении:
- График представляет собой прямую.
- Тангенс угла наклона графика равен $v$.
- График пересекает ось ординат в точке $(0,x_0)$.
- График пересекает ось абсцисс в точке $(-{x_0over v},0)$.
- График пройдет через начало координат, если $x_0=0$.
График перемещения и траектория движения – это не одно и то же! График показывает зависимость координаты от времени по одной из осей. Траектория движения же показывает путь, который прошла точка вдоль прямой, на плоскости или в пространстве. Таким образом, если материальная точка движется на плоскости – для описания ее перемещения требуется два графика, а если в пространстве – то три, по количеству координатных осей.
График скорости
Вид графика скорости при равномерном прямолинейном движении можно построить, учитывая, что для равномерного движения $v=const$. График константы всегда представляет собой горизонтальную прямую, параллельную оси абсцисс. При этом, чем больше значение скорости, тем выше будет лежать эта прямая.
Из этого же графика ясно, что значение перемещения при данной скорости равно площади прямоугольника под прямой. Высота прямоугольника равна модулю скорости. Ширина прямоугольника равна времени пути.
Что мы узнали?
Координата перемещения при прямолинейном равномерном движении описывается формулой $x=x_0+vt$. Если движение происходит на плоскости или в пространстве – необходимо использовать векторный вид формулы и проецировать вектора на оси координат. График перемещения при равномерном движении представляет собой прямую.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Валера Исхаков
10/10
-
Елизавета Фомичёва
10/10
-
Андрей Коробкин
10/10
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 145.
А какая ваша оценка?
Содержание:
Путь и перемещение:
Вы знаете, что любой вид движения совершается по определенной траектории.
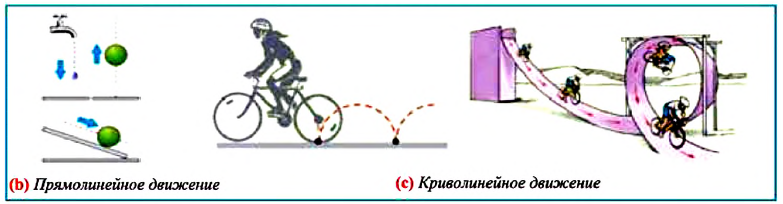
Траектория — это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
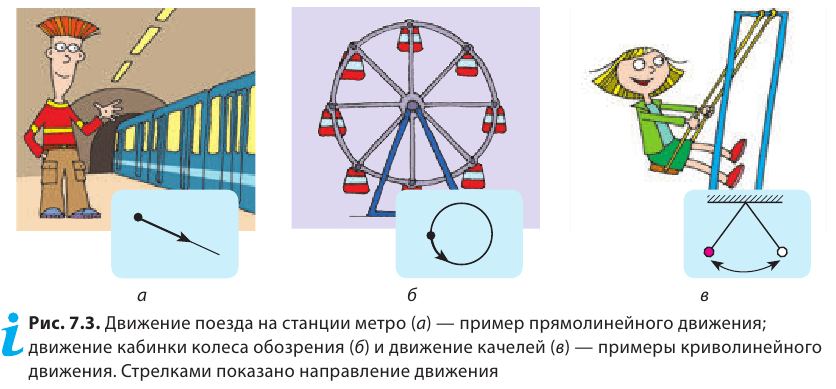
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, — криволинейным (с).
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 
Изменение координат материальной точки во время движения
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается 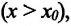
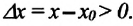
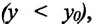
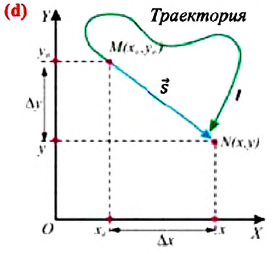
Изменение радиус-вектора материальной точки во время движения
На следующем рисунке представлены радиус-векторы 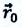
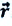
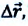
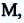
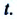

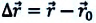
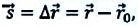
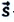
Перемещение — это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.
Векторная величина — это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами — сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
Материальная точка прошла расстояние 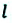
Материальная точка прошла расстояние 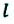
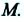
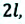
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение 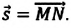
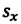
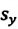
Одинаковы ли путь и перемещение
Задача:
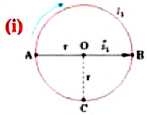
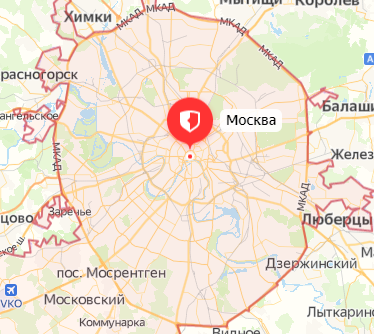
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
Решение:
Пройденный путь 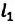
Модуль перемещения же равен диаметру окружности:
Вычисление:
Что такое путь и перемещение
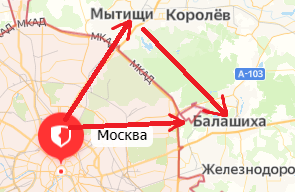
Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
Обозначим перемещение символом 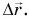
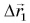
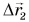
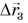
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением 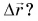
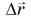
Сравнивать путь S можно с модулем перемещения 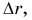
В рассматриваемом примере путь, пройденный автобусом за два часа, 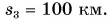
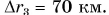
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль 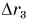
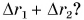
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
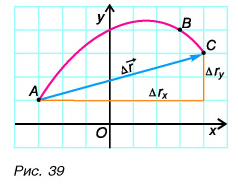
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 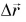
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
- Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
Путь конькобежца:
Путь пешехода:
Ответ:
- Заказать решение задач по физике
Траектория движения
Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).
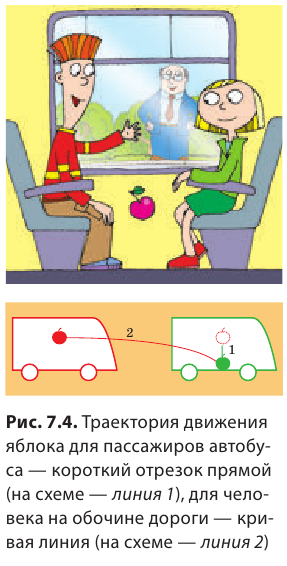
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
Чем путь отличается от перемещения
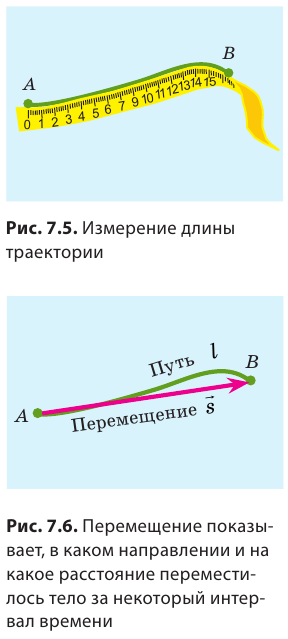
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
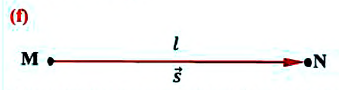
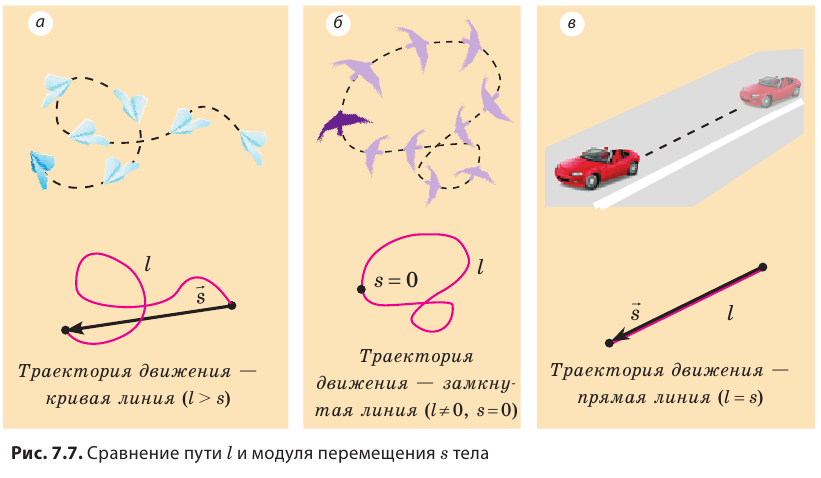
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом 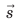
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 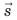
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось