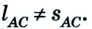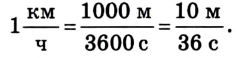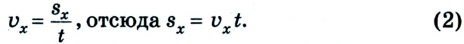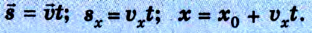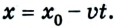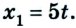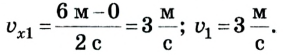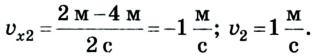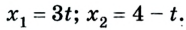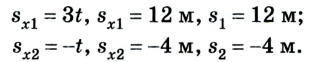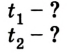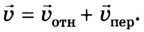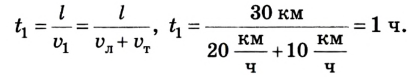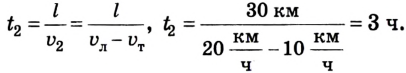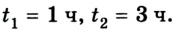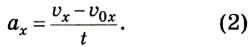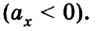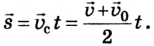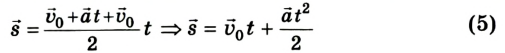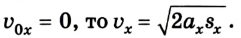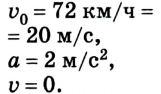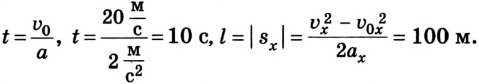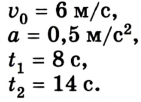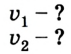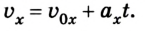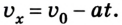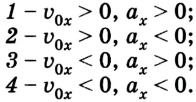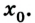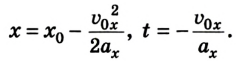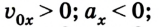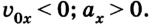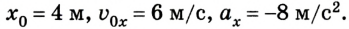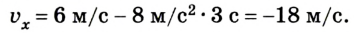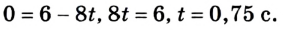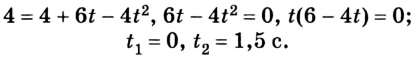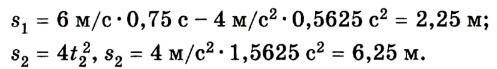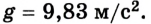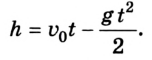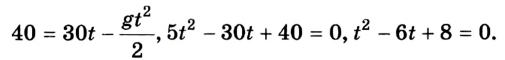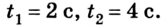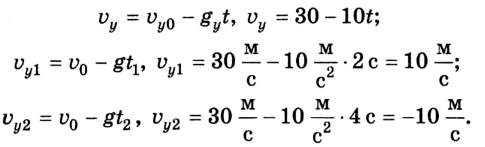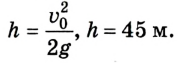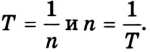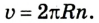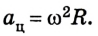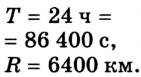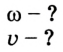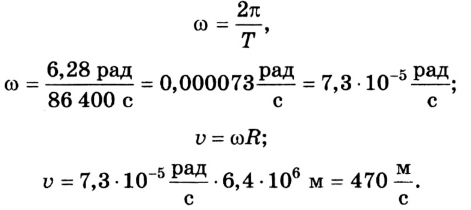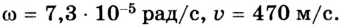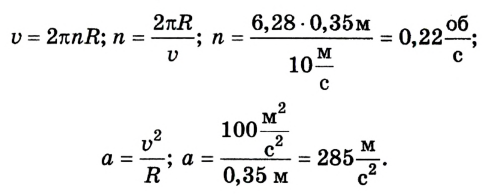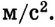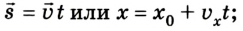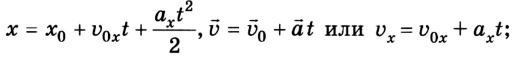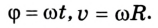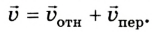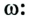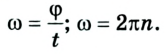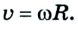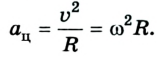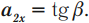В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
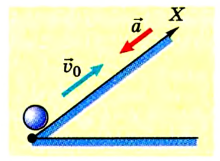
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Здесь — x нулевое- начальная координата. v нулевое — начальная скорость. Продифференцируем по времени, и получим скорость
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Содержание:
Основная задача механики — описание движения тел, т. е. выяснение закона (уравнения) их движения. Как отмечал А. Эйнштейн, наиболее фундаментальная проблема, остававшаяся нерешенной на протяжении тысячелетий, — это проблема движения. Собственно, учение о движении стало наукой лишь со времен Галилео Галилея и Исаака Ньютона.
Кинематика, изучает конкретные механические та их взаимодействия с другими телами. Она фактически объединяет простейшие пространственно-временные зависимости, в частности изменение координат тела со временем (как функцию времени).
Поэтому кинематику часто называют геометрией движения.
Кинематика изучает механические движения тел без учета их взаимодействия с другими телами.
Кинематика
Физика изучает разнообразные явления и процессы, происходящие вокруг нас. Как вам известно, в зависимости от их природы различают механические, тепловые, электрические, магнитные, световые и другие физические явления. Раздел физики, который объясняет движение и взаимодействие тел, называется механикой.
Слово «механика» впервые ввел Аристотель. Оно означает «машина».
Механика — одна из древнейших наук. Ее возникновение и развитие связано с практическими потребностями человека. Первые труды по механике, в которых рассматривались свойства простых механизмов и машин, появились еще в Древней Греции. Весомый вклад в ее становление сделали такие корифеи науки, как Аристотель (IV в. до н. э.), Архимед (III в. до н. э.), Леонардо да Винчи (XV в.), Галилео Галилей (XVII в.) и др. В завершенном виде как классическая теория она получила обоснование в работе Исаака Ньютона «Математические начала натуральной философии» (1687 г.). Современная механика, в основе которой лежит теория относительности, создана в начале XX в. Альбертом Эйнштейном.
Основная задача механики состоит в том, чтобы на основании параметров движения тела: координат, пройденного пути, перемещения, угла поворота, скорости, силы и т. д. — найти закон или уравнение, которое описывает это движение.
Основная задача механики состоит в том, чтобы найти уравнение движения тела с помощью параметров, описывающих это движение.
Т. е. если мы при помощи этих физических величин сможем установить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от способов ее решения в механике выделяют три раздела: кинематика, динамика и статика.
Кинематика изучает, как движется тело, не вникая в причины, вызывающие именно такое движение. Поэтому кинематические уравнения состоят лишь из пространственных характеристик механического движения: пройденного пути, изменения координат тела, скорости и т. д. В них нет сил, изменяющих это движение.
В переводе с греческого слово кинематика» (kinematos) означает движение.
Механическое движение и траектория движения
Чаще всего в обыденной жизни мы наблюдаем явление, которое называется механическим движением. Например, автомобиль едет по дороге, в небе «плывут» тучи, ребенок катается на качелях, Луна вращается вокруг Земли и т. д. Во всех этих случаях происходит изменение положения одного тела или его частей относительно других. Чтобы убедиться в этом, необходимо выбрать тело отсчета, относительно которого можно фиксировать положение движущегося тела в любой момент времени. Тело отсчета выбирают произвольно. В приведенных примерах это может быть столб или дерево возле дороги, дом, поверхность Земли и т. д.
Для того чтобы описать движение тела, необходимо точно знать его местоположение в пространстве в произвольный момент времени, т. е. уметь определять изменение положения тела в пространстве относительно других тел с течением времени. Как известно, легче всего это можно сделать с помощью системы координат. Например, зафиксировать «адрес» тела как определенное его положение в пространстве, измерив расстояния или углы в некоторой системе координат.
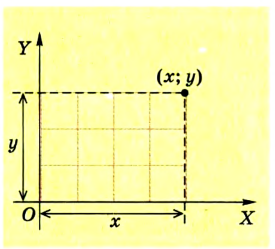
Например, в географии положение тела на земной поверхности задается двумя числами на пересечении меридиана и параллели, которые называются географической долготой и широтой. В математике «адрес» точки чаще всего определяют ее координатами, в частности в прямоугольной (декартовой) системе координат на плоскости — это расстояния х и у (рис. 1.1).
Взаимные изменения положения тела или его частей в пространстве с течением времени называются механическим движением.
Систему координат, как правило, связывают с телом отсчета. В данном случае движущееся тело характеризуется изменением положения в пространстве относительно тела отсчета, т. е. изменением его координат с течением времени.
Математически это можно записать в таком виде: х = x(t); у = y(t).
Для того чтобы определить такое изменение в любой момент времени, с телом отсчета и системой координат необходимо связать средство измерения времени, к примеру секундомер или хронометр. Тогда тело отсчета, связанную с ним систему координат и секундомер как единое целое называют системой отсчета.
Как известно, реальные физические тела имеют форму и объем. Поэтому однозначно задать их положение в пространстве не всегда представляется возможным, поскольку различные их части имеют разные координаты. Однако эту проблему можно упростить, если не брать во внимание размеры тела. Такое возможно лишь при определенных условиях.
Чтобы выяснить их, рассмотрим движение автомобиля. На значительных расстояниях, например на шоссе между Киевом и Харьковом, размерами автомобиля можно пренебречь, поскольку они значительно меньше расстояния между этими городами. Поэтому нет необходимости рассматривать особенности движения каждой части кузова автомобиля — достаточно его представить как движение точки.
Таким образом, для упрощения описания движения тел, когда их размерами при определенных условиях можно пренебречь, применяют понятие материальной точки. Это условное тело, не имеющее размеров, которое определяет положение реального тела в пространстве при помощи координат такой, материальной точки. Ее геометрический образ — невесомая точка, не имеющая размеров. В случае поступательного движения, при котором все точки тела движутся одинаково, любое тело можно считать материальной точкой.
Материальная точка — это физическая модель, при помощи которой представляют реальное тело, пренебрегая его размерами.
Часто кроме движущихся предметов мы наблюдаем тела, пребывающие в состоянии покоя. Однако абсолютно неподвижных тел в природе не существует.
Рассмотрим такой пример. В вагоне на столе стоит бутылка с водой (рис. 1.2). Во время движения поезда разные наблюдатели — пассажир в купе и провожающий на перроне — оценят ее состояние движения по-разному. Для сидящего пассажира она неподвижна, поскольку расстояние от него до бутылки не изменяется. Для провожающего на перроне 16 она движется, потому что изменяет свое положение с течением времени в системе отсчета, связанной с перроном.
Следовательно, состояние покоя является относительным, равно как и состояние движения, поскольку зависит от выбранной системы отсчета. Поэтому в дальнейшем при рассмотрении движения тела мы в первую очередь будем определяться с выбором системы отсчета, потому что от этого нередко зависит сложность уравнений, описывающих данное движение. Правильный выбор системы отсчета ведет к упрощению уравнений движения.
Состояние покоя и состояние движения тела относительны, поскольку зависят от выбора системы отсчета.
Рассмотрим движущееся тело, последовательно фиксируя его положение в определенные моменты времени. Если теперь соединить все точки, в которых побывало тело во время своего движения, то получим мнимую линию, которая называется траекторией движения. Траектория движения может быть видимой (след от самолета на небосклоне, линия от карандаша или ручки при записи в тетради) и невидимой (полет птички, движение теннисного мяча и т. д.).
По форме траектории механическое движение бывает прямолинейным и криволинейным (рис. 1.3).
Положение броуновской частички через определенные промежутки времени.
Рис. 1.3. Различные формы траектории
Траектория прямолинейного движения — прямая линия. Например, падение тела с определенной высоты или движение шарика по наклонному желобу. Во время криволинейного движения тело перемещается по произвольной кривой. Часто реальное движение тел является комбинацией прямолинейного и криволинейного движений. Например, комбинированным есть движение автобуса по маршруту: на разных участках траектория его движения может быть и прямолинейной, и криволинейной.
Поскольку движение тел происходит в определенных системах отсчета, то и траектория рассматривается относительно них. Ведь она отображает во времени последовательные положения тела в некоторой системе отсчета. Поэтому она будет отличаться формой в различных системах отсчета, т. е. траектории движения также относительны. Например, все точки колеса велосипеда относительно его оси описывают окружность, однако в системе отсчета, связанной с землей, эта линия более сложная (рис. 1.4).
Рис. 1.4. Траектория движения точки обода колеса велосипеда
Путь и перемещение
Зная траекторию движения, можно определить путь, пройденный телом: для этого необходимо измерить длину траектории между начальной и конечной точками движения.
Путь — это длина траектории, которую проходит тело или материальная точка за определенный интервал времени. Он обозначается латинской буквой l. Данная физическая величина является скалярной и характеризуется лишь значением длины траектории движения.
В Международной системе единиц (СИ) путь измеряется в метрах (м). На практике используют также другие единицы пути — километр (км), сантиметр (см) и др.
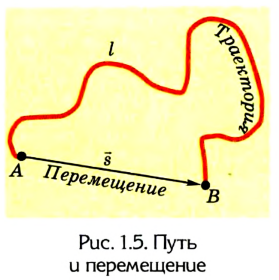
Часто, для того чтобы более полно охарактеризовать движение тела и найти его новое положение, кроме пройденного пути (длины траектории), необходимо указать также направление, в котором двигалось тело. Например, водителю автомобиля приходится ехать по извилистой дороге (рис. 1.5).
Пройденный путь — это длина дороги I, по которой ехал автомобиль. Водитель же совершил перемещение в пространстве из точки А в точку В, которое можно найти, соединив начальное и конечное положение тела прямой линией, указав при этом направление движения.
Следовательно, направленный отрезок прямой, соединяющий начальное положение движущегося тела с конечным, называется перемещением. Перемещение — это векторная величина. Оно обозначается латинской буквой 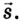
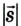
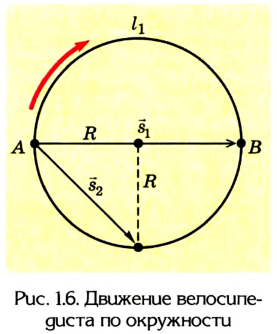
Путь и перемещение могут отличаться своими значениями. Чтобы убедиться в этом, рассмотрим движение велосипедиста по окружности радиуса R= 100 м (рис. 1.6).
Допустим велосипедист стартует в точке А. Проехав половину окружности, он окажется в точке В. Пройденный им путь равен дуге 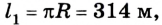
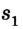
В момент времени, когда велосипедист проедет 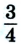
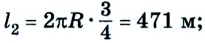
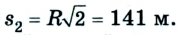
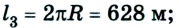
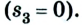
Путь и перемещение имеют также одинаковые значения, когда тело движется прямолинейно лишь в одном направлении.
В рассмотренном нами примере пройденный путь и перемещение разные, отличаются по своему значению. Возникает вопрос: могут ли они совпадать, быть одинаковыми? Можно легко убедиться в том, что такое возможно, если, во-первых, траектория движения будет прямой, во-вторых, движение происходит в одну сторону. Как подтверждение этого, рассмотрим — такой пример.
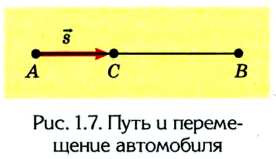
Допустим, что автомобиль движется прямолинейно по шоссе из пункта А в пункт В, а затем возвращается в пункт С. Расстояние между пунктами 2 км и 4 км соответственно, все они размещены на одной прямой (рис. 1.7).
Двигаясь из пункта А в пункт В, автомобиль проходит путь 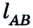
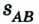
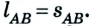
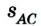
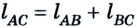
Следовательно, пройденный путь и перемещение по своему значению одинаковы лишь в том случае, если тело движется по прямой и не изменяет направление движения.
Равномерное прямолинейное движение
Простейшим видом механического движения является равномерное прямолинейное движение. Это такое движение, при котором тело, двигаясь по прямой, за любые одинаковые интервалы времени совершает одинаковые перемещения. Его траектория — прямая линия. Поэтому его можно описать переменой одной из координат, например х = x(t), если координатная ось совпадает с направлением движения.
Пусть тело в начальный момент движения имеет координату 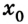
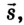
Как известно, в СИ скорость
измеряется в метрах за секунду (м/с). 1 м/с — это скорость такого равномерного прямолинейного движения, при которой тело за 1 с совершает перемещение 1 м. На практике используют также другие единицы скорости, например километр в час:
Поскольку перемещение 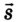
При равномерном движении значение скорости остается постоянным, поскольку за любые равные интервалы времени совершаются равные перемещения.
Как известно, основной задачей механики является определение положения тела в пространстве в произвольный момент времени. Следовательно, чтобы ее решить, надо найти координаты тела либо их изменение во времени: х — x(t). В механике такое уравнение называется уравнением движения. При решении задач с использованием уравнения движения векторные величины, характеризующие движение тела, записывают в проекциях на соответствующую ось. Следовательно, из формулы (1) получаем:
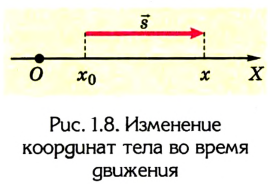
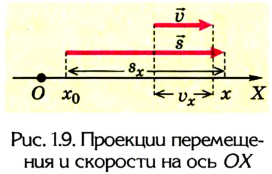
Из рисунков 1.8 и 1.9 понятно, что 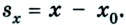
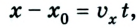
Уравнения равномерного прямолинейного движения:
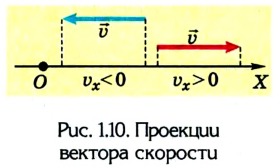
Рассмотрим теперь различные случаи равномерного прямолинейного движения (рис. 1.10).
Из рисунка следует, что если направление движения тела совпадает с направлением координатной оси, то 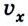
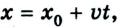
Если же направление движения тела противоположно направлению координатной оси, то 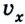
Как решать задачи кинематики
Решение любой физической задачи в определенной степени можно условно разделить на три этапа: физический, математический и анализ решения.
На физическом этапе:
- ✓ анализируют условие задачи и описание физической ситуации, заданной условием;
- ✓ выясняют физическую модель явления, лежащего в основе задачи;
- ✓ физическую модель явления представляют в графической форме (рисунки, чертежи, схемы, графики и т. д.);
- ✓ сокращенно записывают условия задачи в систематизированном виде.
На математическом этапе:
- ✓ предлагают математическую модель задачи, составляют общие уравнения, описывающие физические явления, представленные в условии задачи;
- ✓ определяют конкретные условия и параметры, при которых происходит данное явление;
- ✓ конкретизируют общие уравнения в виде частных решений аналитическим, графическим или числовым способом, производят вычисления.
- На этапе анализа решения:
- ✓ производят проверку единиц физических величин и находят значения искомых величин;
- ✓ анализируют результаты, их достоверность и правдоподобность;
- ✓ ищут иные методы решения задачи и выбирают наиболее рациональный из них.
В ходе решения задач кинематики главное состоит в том, чтобы за заданными параметрами движения (координаты, перемещение, скорость и др.) записать уравнение движения. Или наоборот, если уравнение движения известно, ищут физические величины, которые его описывают.
Решение задач кинематики подчинено определенной последовательности умственных действий, так называемому алгоритму, при помощи которого поиск решения задачи значительно облегчается. Представим его как последовательность шагов в ходе решения задачи.
- Шаг 1. В соответствии с условием задачи выберите систему отсчета. Определите начальные значения координат, связав их с телом отсчета.
- Шаг 2. Выясните характер движения (равномерное, неравномерное) и вид траектории (прямолинейная, криволинейная).
- Шаг 3. Сделайте рисунок, иллюстрирующий условие задачи. Свяжите рисунок с выбранной системой отсчета, обозначьте на нем векторные физические величины.
- Шаг 4. Отобразите проекции перемещения, скорости, других векторных величин и запишите уравнение движения тела в общем виде. При необходимости составьте дополнительные уравнения, которые объединяют эти кинематические величины.
- Шаг 5. Решите уравнения относительно искомых величин. Определите их значения, оцените достоверность результата.
- Шаг 6. Проанализируйте полученный ответ. Если он противоречит смыслу задачи, начните поиск иного решения.
- Шаг 7. Произведите поиск иных возможных путей решения задачи. Оцените, какое из решений наиболее рационально.
Задача №1
Из пунктов А и В, расстояние между которыми 80 км, одновременно начали движение навстречу друг другу два велосипедиста. Первый ехал со скоростью 5 м/с, второй -3 м/с. Определите:
- 1) через какое время они встретятся и где это произойдет;
- 2) какой путь они пройдут до момента встречи и какое совершат перемещение;
- 3) через какое время от начала движения расстояние между ними будет 20 км.
Решение
1. Выберем такую систему отсчета, начало координат которой совпадает с пунктом А. В общем виде уравнение движения тела имеет такой вид: 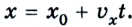
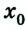
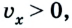
У второго велосипедиста 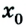
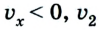
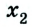
Вследствие движения координаты обоих велосипедистов с течением времени изменяются: у первого она возрастает, у второго — уменьшается. В момент их встречи координаты обоих велосипедистов равны: 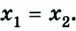
5t = 80 000 — 3t; St = 80 000; отсюда t = 10 000 с = 2,8 ч. Таким образом, велосипедисты встретятся через 2,8 часа.
Место их встречи определяют координаты 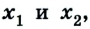
Задача №2
Поскольку велосипедисты по условию задачи ехали прямолинейно и не изменяли направления движения, то пройденный ими путь равен модулю перемещения (или его проекции):
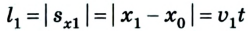
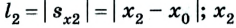
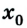
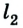
Или 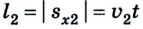
3. Чтобы найти время, когда расстояние между велосипедистами будет равно 20 км, достаточно записать равенство 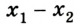
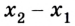
5t — 80 000 + 3t = 20 000; 8t = 100 000; t = 12 500 с = 3,5 ч.
80 000 — 3t — 5t = 20 000; 8t = 60 000; t = 7500 с = 2,1 ч.
Почему получено два разных ответа? Внимательно проанализировав условие задачи, заметим, что на расстоянии 20 км друг от друга велосипедисты будут дважды — когда едут навстречу друг другу (2,1 ч) и когда разъезжаются после встречи, продолжая движение (3,5 ч).
Графики равномерного прямолинейного движения
Для того чтобы лучше усвоить особенности изменений параметров равномерного движения (координат, пути, перемещения, скорости) с течением времени, рассмотрим соответствующие графические зависимости, следующие из уравнения равномерного прямолинейного движения.
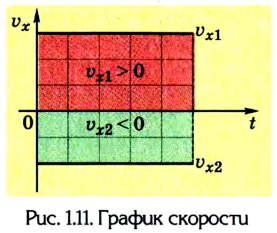
1. График скорости v = u(t). Как известно, скорость тела при равномерном прямолинейном движении с течением времени не изменяется, т. е. v = const. Поэтому график скорости — это прямая, параллельная оси времени t, которая находится над ней, если проекция скорости положительна (рис. 1.11), или под ней, если она отрицательна.
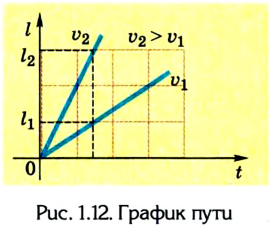
2. График пути l = l(t). Из формулы пути l = vt следует, что между пройденным путем и временем существует прямо пропорциональная зависимость. Графически она отображается прямой, проходящей через начало координат (ведь длина пути не может иметь отрицательных значений). В зависимости от значения скорости наклон графика будет разным (рис. 1.12): чем больше скорость, тем круче прямая.
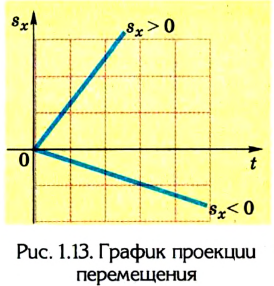
3. График проекции перемещения 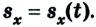
График проекции перемещения всегда проходит через начало координат. Угол наклона прямой, как и в случае графика пути, зависит от значения скорости: чем она больше, тем круче график проекции перемещения.
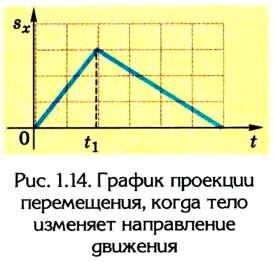
Если тело изменяет направление движения — сначала движется в одну сторону, а затем возвращается назад, то график проекции перемещения принимает вид, изображенный на рисунке 1.14 (в момент времени 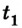
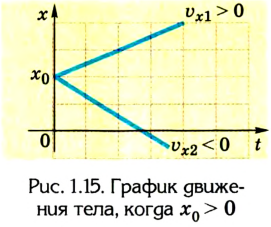
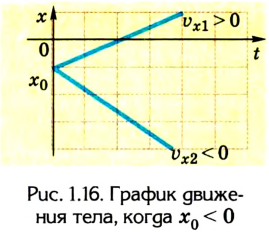
4. График движения тела х = x(t) характеризует изменение координат тела с течением времени. Из уравнения движения 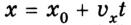
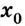
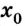
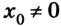
Так как проекция скорости может иметь положительные и отрицательные значения (направление вектора скорости может совпадать или быть противоположным выбранному направлению оси), то график может подниматься вверх (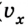
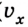
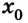
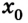
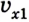
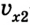
Таким образом, при помощи графиков можно выяснить характер движения тел и изменения соответствующих величин с течением времени t.
Задача №3
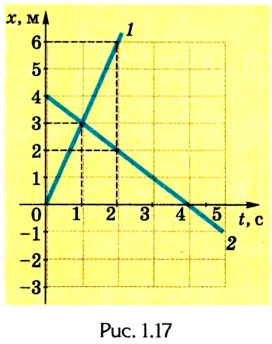
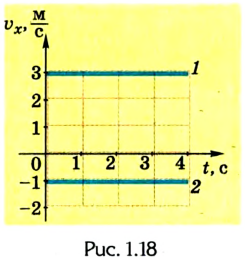
На основании графика движения (рис. 1.17):
- 1) определить скорость движения тел;
- 2) составить уравнения движения обоих тел;
- 3) найти перемещение тел за 4 с;
- 4) определить время и место их встречи;
- 5) найти расстояние между телами через 2 с после начала движения;
- 6) построить графики скорости, проекции перемещения и пути.
Решение
1. Скорость тела определяется на основании формулы
Время движения выбираем произвольно, руководствуясь простотой расчетов. Например, используем значение t = 2 с. Тогда тело 1 через 2 с будет иметь координату 6 м; его начальная координата 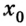
У тела 2 начальная координата равна 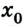
2. Уравнение движения для обоих тел будет иметь такой вид:
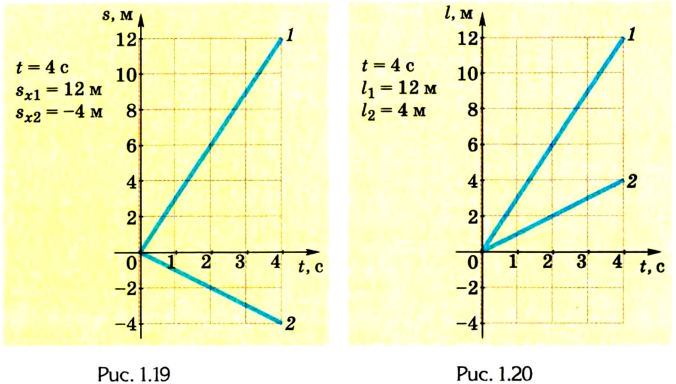
3. Перемещение тел за время t = 4 с равно:
4. В момент встречи тел их координаты будут одинаковы, т. е. это точка пересечения графиков. При помощи перпендикуляра, проведенного к оси координат, можно установить координату места встречи — она равна 3 м. Для определения времени встречи необходимо опустить перпендикуляр на ось времени t; получим t = 1 с.
5. Согласно графикам движения тел через 2 с тело 1 имеет координату
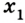
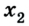
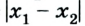
6. Используя предыдущие данные решения задачи, построим соответствующие графики (рис. 1.18-1.20).
Относительность движения. Закон сложения скоростей
Для того чтобы описать механическое движение и определить его параметры — траекторию, перемещение, пройденный путь, скорость и др., следует прежде всего выбрать систему отсчета и проанализировать движение тела или материальной точки относительно тела отсчета, выбранного произвольно. В природе существует множество систем отсчета и описание движения может одновременно производиться в каждой из них. Например, лодка, плывущая по реке, движется относительно ее берегов, относительно теплохода, который плывет рядом, относительно пешеходов, стоящих на берегу, и т. д.
Чаще всего систему отсчета связывают с телом, которое в данной ситуации считается неподвижным: с землей, берегом реки, населенным пунктом, столбом на обочине дороги и др. Такая система отсчета считается неподвижной.
С телами, которые движутся в неподвижных системах отсчета равномерно и прямолинейно, связывают подвижные системы отсчета. Следует учитывать, что удачный выбор системы отсчета намного упрощает решение задачи.
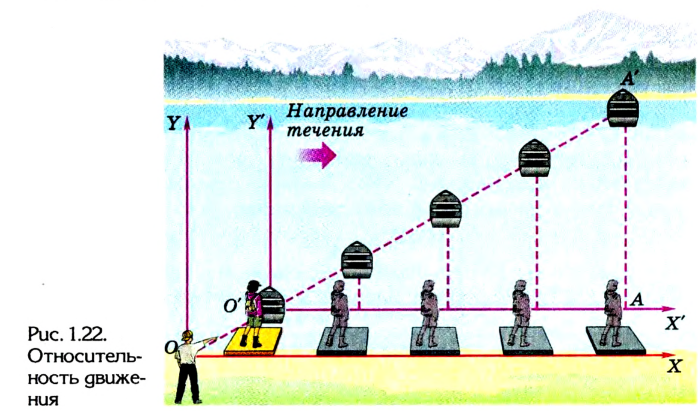
Рассмотрим движение какого-либо тела, например лодки, плывущей по реке, в различных системах отсчета (рис. 1.22).
Пусть лодка пересекает реку перпендикулярно к ее течению. За движением лодки следят два наблюдателя — один на берегу реки (неподвижная система отсчета XOY), другой с плота, который перемещается относительно берега со скоростью течения реки (подвижная система отсчета X’O’Y’).
Первый наблюдатель будет видеть перемещение лодки по прямой ОА’. Второй наблюдатель, находясь в подвижной системе отсчета, увидит иную картину: лодка будет удаляться от него по прямой, перпендикулярно к течению, и когда она достигнет противоположного берега в т. А’, плот будет находится точно напротив нее в т. А.
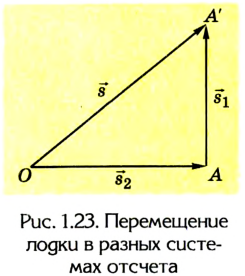
Таким образом, относительно подвижной системы отсчета лодка совершает перемещение 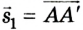
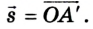
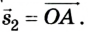
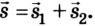
Разделив каждый член уравнения на время движения t, одинаковое для подвижной и неподвижной систем отсчета, получим:
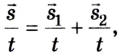
Уравнение (1) называется законом сложения скоростей: скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости самой подвижной системы отсчета относительно неподвижной. Сложение скоростей в данном случае также выполняется согласно правилам сложения векторов.
Движение тела в подвижной системе отсчета называется относительным, движение самой подвижной системы отсчета относительно неподвижной является переносным. Таким образом, механическое движение тел относительно различных систем отсчета может быть представлено независимыми движениями: а) относительным движением тела в подвижной системе отсчета; б) переносным движением подвижной системы отсчета относительно неподвижной. В соответствии с данным утверждением закон сложения скоростей приобретает вид:
т. е. скорость тела в неподвижной системе отсчета равна геометрической сумме относительной и переносной скоростей.
Скорость тела в неподвижной системе отсчета иногда называют абсолютной.
- Заказать решение задач по физике
Задача №4
Моторная лодка плывет по реке от одного поселка к другому, расстояние между которыми 30 км. Скорость лодки в стоячей воде 20 км/ч, а скорость течения реки относительно берегов 10 км/ч. За какое время лодка преодолеет расстояние между поселками, двигаясь сначала по течению, а затем, возвращаясь назад, против него?
Дано:
Решение
Согласно закону сложения скоростей
В скалярной форме, учитывая знаки проекции скоростей, получим:
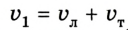
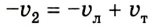
Следовательно, время движения лодки между поселками по течению:
Время движения лодки против течения:
Ответ:
Равноускоренное движение. Ускорение
При равномерном прямолинейном движении скорость тела в различных точках траектории остается неизменной. Однако в реальной жизни мы чаще имеем дело с неравномерным движением, когда скорость тела может изменяться и по своему значению, и по направлению. Если за любые равные интервалы времени скорость тела изменяется одинаково либо по значению, либо по направлению, то такое движение называется равноускоренным.
Изменение значения скорости может происходить довольно быстро (например, движение пули в ружье, старт ракеты, разбег самолета и т. п.) или сравнительно медленно (начало движения поезда, торможение автомобиля). При этом также следует учитывать, что скорость как векторная величина может изменять свое направление, которое тоже характеризует неравномерность движения. В физике для оценивания быстроты изменения скорости движения применяют физическую величину, которая называется ускорением.
Для характеристики неравномерного движения используют понятие ускорения, которое определяет, насколько быстро I изменяется скорость движения.
Ускорение — это векторная физическая величина, равная отношению изменения скорости тела к интервалу времени, в течение которого это изменение произошло:
где 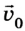
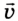
Из определения равноускоренного движения следует, что его ускорение является постоянной величиной (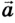
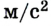
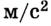
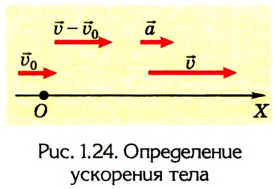
Значение ускорения определяют, учитывая векторные свойства данной физической величины. В частности, в проекциях на ось ОХ (рис. 1.24) формула ускорения приобретает вид:
В случае, когда 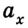
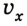
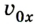
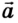
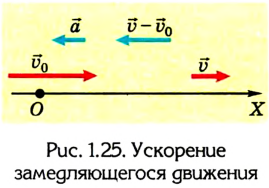
Если скорость тела со временем уменьшается 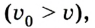
В данном случае в соответствии с выбранным направлением координатной оси ОХ проекция ускорения будет отрицательной
Вместе с тем знак проекции ускорения не определяет характер движения — оно ускоряющееся или замедляющееся, в зависимости от выбора системы отсчета. В этом легко убедиться, если рассмотреть случай, когда оба тела движутся в противоположных направлениях. Тогда одно из тел имеет положительную проекцию ускорения 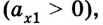
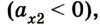
Из формул (1) и (2) можно получить кинематическое уравнение скорости для равноускоренного движения:
или в проекциях на ось ОХ:
Выведем теперь кинематическое уравнение перемещения для равноускоренного движения. Учтем, что скорость во время такого движения постоянно изменяется, например сначала она равна 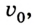
Подставив в данную формулу уравнение (3) и произведя некоторые преобразования, получим:
или в проекциях на ось ОХ:
Если начальная скорость тела равна 0 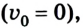
или в проекциях на ось ОХ:
Для прямолинейного движения, учитывая, что 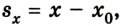
или для случая, когда 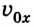
Следует помнить, что в ходе решения задач необходимо учитывать знаки проекций в соответствующих уравнениях.
При определении проекции перемещения не всегда известно время, в течение которого происходило движение. Тогда можно воспользоваться иным уравнением. Чтобы его получить, подставим в кинематическое уравнение 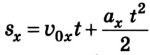
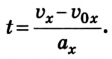
Отсюда 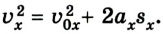
Задача №5
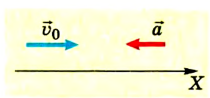
Водитель начинает тормозить в тот момент, когда спидометр автомобиля фиксирует скорость 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 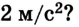
Дано:
t -?
l — ?
Решение
По условию задачи спидометр показывает начальную скорость автомобиля 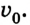
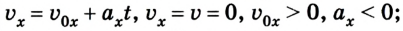
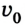
Ответ: автомобиль остановился через 10 с, проехав 100 м.
Задача №6
Шарик толкнули по наклонному желобу вверх со скоростью 6 м/с. Шарик движется с ускорением 0,5 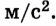
Дано:
Решение
Направим ось ОХ вдоль желоба (см. рис.).
Учитывая знаки проекций скорости и ускорения, имеем
Отсюда уравнение для 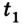
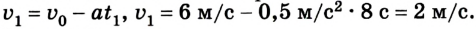
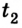
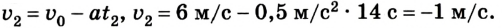
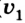
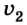
Ответ: 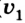
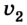
Графики равноускоренного движения
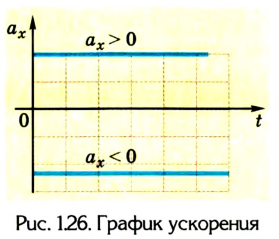
1. График ускорения а = a(t). Как известно, при равноускоренном движении ускорение является величиной постоянной (а = const). Поэтому зависимость проекции ускорения от времени отображает прямая, параллельная оси времени t. В зависимости от значения проекции ускорения -положительная она или отрицательная — данная прямая размещена над осью или под ней (рис. 1.26).
2. График скорости и = v(t).
Линейная зависимость скорости от времени обусловлена математическим видом ее кинематического уравнения 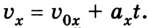
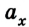
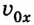
Если 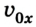
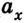
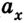
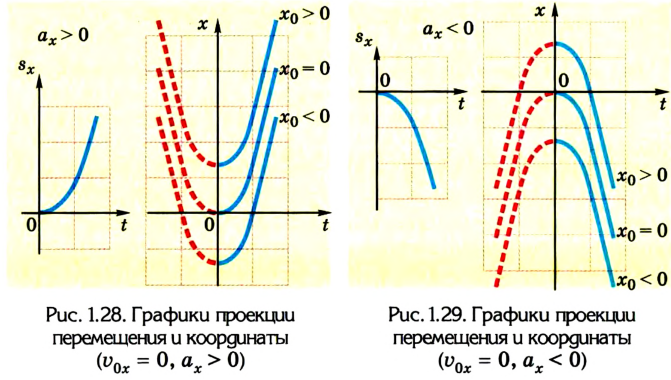
3. График проекции перемещения 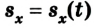
Кинематические уравнения перемещения и координат представляют собой квадратные уравнения вида 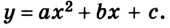
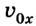
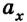
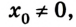
Если 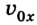
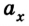
Если 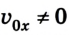
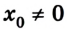
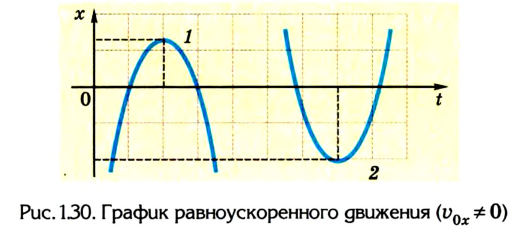
Представленные на рисунке 1.30 графики отображают такие параметры равноускоренного движения:
1)
2)
Задача №7
Прямолинейное движение тела описывается уравнением 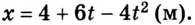
- 1) характер движения тела и его скорость через 3 с от начала движения;
- 2) в какой момент времени после начала его отсчета тело изменило направление движения на противоположное;
- 3) в какой момент времени после начала его отсчета тело вернется в начальную точку;
- 4) перемещение и пройденный путь через 2 с.
Решение
1. Для определения скорости тела в любой момент времени необходимо составить уравнение скорости 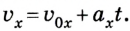
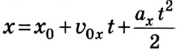
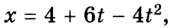
При таких условиях уравнение скорости для данного движения приобретает вид: 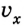
Следовательно, скорость движения равна 18 м/с. Отрицательное ее значение свидетельствует о том, что направление скорости противоположно выбранному направлению координатной оси. Движение тела замедляется 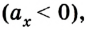
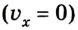
2. Для определения момента изменения направления движения надо уравнение скорости приравнять к 0 и решить его относительно t:
3. Тело вернется в начальную точку, когда его координата примет значение начальной координаты, т. е. х = 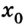
Следовательно, тело имело координату в начале движения 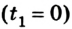
4. Для определения перемещения через 2 с после начала движения составим уравнение проекции перемещения
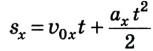
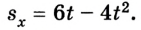
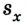
Для определения пройденного пути следует учесть, что тело меняло направление движения, поэтому 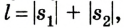
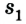
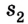
Таким образом, пройденный путь равен:
l = 2,25 м + 6,25 м = 8,5 м.
Свободное падение тел. Ускорение свободного падения
Многочисленные наблюдения и опыты убеждают нас в том, что все тела падают на землю вследствие притяжения к ней. Если тело бросить вертикально вверх, оно все равно упадет на землю: вначале его скорость будет уменьшаться, а затем оно начнет падать вниз со всевозрастающей скоростью.
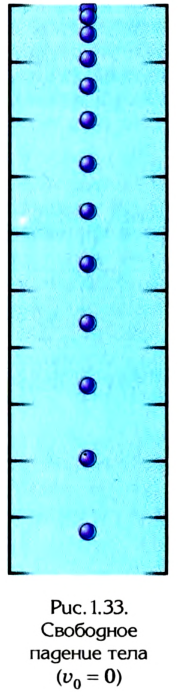
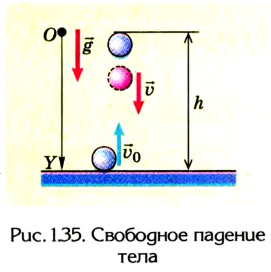
Анализ характера движения падающего тела (рис. 1.33) показывает, что данное движение равноускоренное, т. е. за равные интервалы времени оно проходит разные расстояния, которые с течением времени пропорционально увеличиваются.
Долгое время считалось, что различным телам Земля придает разное ускорение, и поэтому они падают на нее неодинаково — одни быстрее, другие медленнее. Это, как оказалось впоследствии, ложное представление подтверждал жизненный опыт: легкое перышко, падающее вместе со свинцовым шариком, достигало земли гораздо позже его. Этот, на первый взгляд, очевидный факт вынуждал многих людей искаженно воспринимать действительное протекание явления свободного падения тел. Если повторить данный опыт в условиях, когда на тело не действуют другие факторы, кроме земного притяжения, например в цилиндрической колбе, из которой откачан воздух, то результат будет иным: оба тела упадут одновременно. Этот опыт впервые выполнил И. Ньютон. Он подтвердил, что в условиях свободного падения, т. е. когда на тело действует только сила тяжести, все тела, независимо от их массы и формы, падают одинаково. Следовательно, свободное падение — это равноускоренное движение тел под действием силы тяжести при отсутствии посторонних влияний на них (сопротивление воздуха, электромагнитное взаимодействие и др.). Свободное падение происходит не только на Земле вследствие притяжения к ней всех тел. Оно происходит на всех планетах, Солнце, Луне и др. Однако падение тела ускорение свободного падения у них, конечно же, разное.
Выдающийся итальянский физик Галилео Галилей, изучая движение тел по наклонной плоскости, установил, что шары одинакового диаметра, изготовленные из дерева, железа, слоновой кости и других материалов, следовательно, разной массы, имеют одно и то же ускорение. Увеличивая угол наклона, он пришел к выводу, что значение ускорения при этом растет, но остается одинаковым для всех тел, независимо от их массы. Если увеличивать угол наклона плоскости до 90°, т. е. до ее вертикального положения, выводы в отношении ускорения тел останутся теми же.
Ведь при этом не появилось каких-либо дополнительных факторов, влияющих на характер движения тел. Для подтверждения данного вывода ученый провел известный опыт с пушечным ядром и пулей от мушкета, бросая их с Пизанской башни (рис. 1.34): оба тела достигали земли одновременно. Таким образом Г. Галилей экспериментально установил, что ускорение свободного падения не зависит от массы тел и является постоянной величиной для каждой планеты.
Благодаря многочисленным измерениям ускорения свободного падения для Земли определено его среднее значение у поверхности: 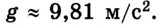
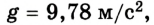
Поскольку свободное падение и движение тела, брошенного вертикально вверх (как частный случай свободного падения), являются равноускоренным движением, все его кинематические уравнения применимы и для данного случая. Вместе с тем в соответствующих уравнениях надо учитывать направление движения.
Выберем ось ОУ для вывода кинематических уравнений свободного падения тела (рис. 1.35).
Учитывая знаки проекций векторных величин на ось ОУ, а также то, что проекцию вертикального перемещения (высоту) обозначают
буквой h, получим:
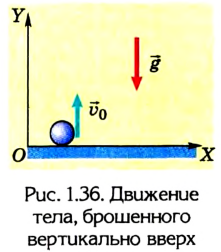
Задача №8
Тело брошено вертикально вверх с начальной скоростью 30 м/с (рис. 1.36).
1. Через какое время оно будет на высоте 40 м?
Воспользуемся уравнением движения
Для упрощения уравнения можно принять 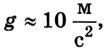
Решив квадратное уравнение, получим два корня
Оба корня удовлетворяют условию задачи. Ведь тело было на высоте 40 м дважды: через 2 с, двигаясь вверх, и через 4 с, падая вниз.
2. Какую скорость имеет тело, пролетая отметку 40 м?
На одной и той же высоте значение скорости тела по модулю одинаково, а по направлению противоположно.
3. На какую максимальную высоту поднимется тело?
В наивысшей точке скорость тела равна 0. Следовательно,
Несложно определить, что все время движения составляет 6 с, общее перемещение тела равно 0, а пройденный путь l = 90 м.
Движение точки по окружности
Ранее мы рассматривали равноускоренное движение, траекторией которого была прямая. При таком движении изменяется значение скорости, а ее направление остается неизменным. В жизни чаще встречаются криволинейные движения (орбитальное движение планет, повороты транспорта нa дороге, карусели и т. п.), во время которых происходят изменения направления скорости движения. Здесь проявляется векторный характер ускорения.
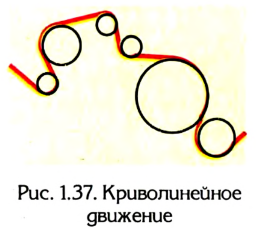
По форме траектории криволинейное движение может быть достаточно разнообразным. Однако его всегда можно представить в виде последовательных участков, состоящих из отрезков прямых и дуг окружностей различного диаметра (рис. 1.37). Т. е. любое криволинейное движение является комбинацией прямолинейного движения и движения тела по окружности.
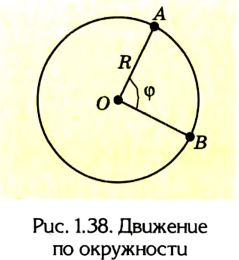
Рассмотрим равномерное движение материальной точки по окружности. Пусть она равномерно движется по окружности радиуса R и за некоторое время t перемещается из точки А в точку В (рис. 1.38).
Угол, который при этом описывает радиус, называется угловым перемещением.
Угловое перемещение обозначают греческой буквой 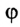
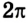
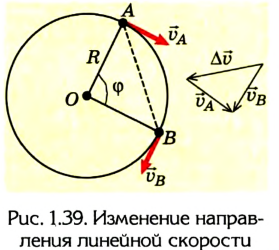
Движение точки по окружности характеризуют также период вращения и частота вращения. Период вращения — это время, в течение которого материальная точка совершает полный оборот по окружности, т. е. поворот на угол 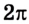
где t — время вращения, N — количество совершенных оборотов. В СИ период вращения Т измеряется в секундах (с). Частота вращения n характеризует количество оборотов тела или материальной точки вокруг центра вращения за 1 секунду:
где N — количество оборотов, совершенных за время t.
В СИ частота вращения измеряется в оборотах за секунду (об/с).
Между частотой и периодом вращения существует взаимообратная зависимость:
Для определения быстроты движения точки по окружности используют понятие угловой скорости. Это физическая величина, равная отношению углового перемещения 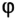
В СИ угловая скорость измеряется в радианах за секунду (рад/с). 1 рад/с равен угловой скорости такого равномерного движения точки по окружности, при котором за 1 с совершается угловое перемещение 1 рад.
Поскольку за период Т угловое перемещение 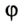
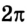
Равномерное движение материальной точки по окружности характеризуется специфическими кинематическими величинами, благодаря которым его описывают при помощи соответствующих уравнений. Это — угловое перемещение и угловая скорость, период и частота вращения. Наряду с ними применяется и привычное для нас понятие скорости, которое в данном случае называют линейной скоростью.
Во время равномерного движения точки по окружности значение ее линейной скорости остается неизменным 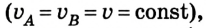
Поэтому линейную скорость можно характеризовать как скорость тела в некоторой точке. Она направлена по касательной к дуге в данной точке (точка А и точка В). В этом можно убедиться, приложив к точильному камню стальной нож: искры от него летят по касательной к поверхности камня в том месте, куда поднесли нож.
Линейная скорость тела, которое движется по окружности, все время изменяется по направлению и в любой точке траектории направлена по касательной к дуге этой окружности.
Поскольку в данном случае линейная скорость по модулю не изменяется, то из формулы скорости равномерного движения и 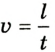
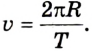
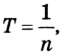
Сравнивая формулы линейной скорости 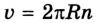
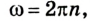
Как уже отмечалось, изменение направления вектора скорости также вызывает ускорение, ведь как векторная величина оно равно 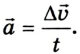
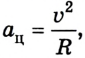
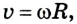
Задача №9
Земля делает один оборот вокруг своей оси за 24 ч. Вычислить угловую и линейную скорости вращения точек поверхности Земли, которые находятся на экваторе. Радиус Земли равен 6400 км. Считайте, что ось вращения проходит сквозь полюсы.
Дано:
Решение
Вращение Земли вокруг своей оси можна считать равномерным.
Следовательно,
Ответ:
Задача №10
Велосипедист едет по дороге со скоростью 10 м/с. Сколько оборотов за секунду делают колеса велосипеда, если они не скользят? Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Дано:
v = 10 м/с,
R = 0,35 м.
n — ? а — ?
Решение
Ответ: n = 0,22 об/с, а = 285
Итоги:
Кинематика изучает механическое движение тел, не рассматривая причин, вызывающих именно такое движение. Описание механического движения в кинематике основывается на выяснении характера изменений координат, перемещений, скорости с течением времени. Для того чтобы описать движение тела, необходимо установить закон (уравнение) изменения во времени координат или скоростей тела относительно других тел. Изменение положения тела в пространстве с течением времени характеризуется перемещением. Это векторная величина, которая определяет не только пройденный путь, но и направление, в котором происходило движение.
Механическое движение по форме траектории может быть прямолинейным или криволинейным, по характеру движения — равномерным или равноускоренным. В зависимости от этого уравнения движения имеют вид:
для равномерного прямолинейного движения
для равноускоренного прямолинейного движения
для равномерного движения по окружности
Механическое движение относительно. Это означает, что траектория, перемещение, пройденный путь, скорость, зависят от выбора системы отсчета. Механическое движение относительно различных систем отсчета может быть представлено двумя независимыми движениями — относительным движением тела в подвижной системе отсчета и переносным движением подвижной системы отсчета относительно неподвижной. Данное утверждение подтверждает закон сложения скоростей -скорость тела в неподвижной системе отсчета равна векторной сумме относительной и переносной скоростей:
Равноускоренное движение характеризует векторная физическая величина, называемая ускорением: 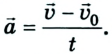
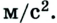
Криволинейное движение можно представить как последовательность участков, состоящих из отрезков прямых и дуг окружностей разного диаметра. Равномерное движение тела или материальной точки по окружности характеризуется угловым перемещением 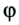
Линейная и угловая скорости согласуются между собой в виде соотношения:
При равномерном движении точки по окружности вследствие изменения направления линейной скорости возникает центростремительное ускорение:
- Законы сохранения в физике
- Международная система единиц СИ
- Математика — язык физики
- Законы Ньютона в физике
- Магнитное поле Земли
- Ядерная энергетика в физике
- Динамика в физике
- Статика в физике
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Содержание
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Основные формулы по теме «Кинематика»
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ), единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ), единица измерения — м/с2.
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
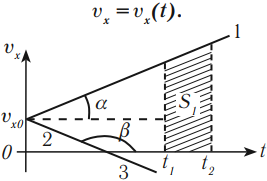
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равноускоренном движении – прямая.
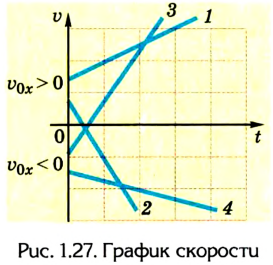
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ), единицы измерения – м/с2.
Важно! ( g ) = 9,8 м/с2, но при решении задач считается, что ( g ) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
3 (60.13%) 150 votes