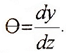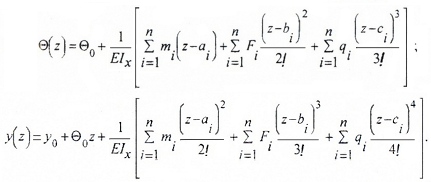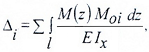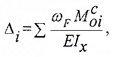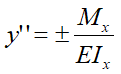Задача. Для балки определить перемещения в т. А, В, С, D, подобрать сечение из двух швеллеров из условия прочности, проверить жесткость, показать изогнутую ось балки. Материал — сталь Ст3, допускаемое перемещение 
- Определим опорные реакции.
Наносим значение опорных реакций на расчетную схему
2. Строим эпюру моментов от заданной нагрузки – грузовую эпюру МF.
Т.к. под равномерно распределенной нагрузкой линия параболическая кривая, то для её проведения потребуется дополнительная точка – поставим т.К в середине нагрузки.
Строим эпюру МF от заданной нагрузки.
3. Подберем сечение из двух швеллеров:
Подбираем 2 швеллера №33 см3.
Проверим прочность подобранного сечения.
Прочность обеспечена.
4. Определим перемещения в заданных точках. Снимаем с балки всю нагрузку. Для определения линейных перемещений (прогибов) прикладываем единичную силу (F=1), а для определения угловых перемещений — единичный момент .
Точки А и В – это опоры, и по граничным условиям в шарнирных опорах прогиб невозможен, а угловое перемещение присутствует. В точках С и D будут и линейные (прогибы), и угловые (углы поворота) перемещения.
Определим угловое перемещение в т.А. Прикладываем в А единичный момент (рис. б). Строим эп , определяем в ней необходимые ординаты. (рис. в).
Ординаты эп.МF – все положительные, эп. – тоже.
Перемещения будем определять методом Мора по формуле Симпсона.
Определим момент инерции Iх для сечения.
Модуль продольной упругости Е для Ст3 Е = 2·105 МПа = 2·108 кПа. Тогда:
Угол поворота φА получился положительным, это значит, что угол поворота сечения совпадает с направлением единичного момента.
Определим угол поворота φВ. (рис.г,д )
Теперь определим перемещения в т. С (линейное и угловое). Прикладываем единичную силу (рис. е), определяем опорные реакции и строим эп. от единичной силы (рис.ж).
Рассмотрим рис. е.
Строим эп. :
Определим прогиб в т. С.
Для определения угла поворота в т. С приложим единичный момент (рис. з), определим опорные реакции и построим эпюру единичных моментов (рис. и).
(знак «— « говорит о том, что реакция RА направлена в обратную сторону. Показываем это на расчетной схеме – рис.з).
Строим эп. ,
Поскольку m=1 приложен в т. С пролета балки, то момент в т. С определим как от левых, так и от правых сил.
Определим прогиб в точке С.
(знак «-» говорит о том, что угол поворота направлен противоположно направлению единичного момента)
Аналогично определим линейное и угловое перемещения в т. D.
Определим уD . (рис. к).
Строим эп. (рис.л) :
Определим φD (рис. м):
Строим эп. — (рис.н).
Определим угол поворота:
(угол поворота направлен в сторону, противоположную единичному моменту).
Теперь покажем изогнутую ось балки (упругую линию), которой стала прямолинейная ось под действием нагрузки. Для этого зарисуем первоначальное положение оси и в масштабе отложим вычисленные перемещения (рис.о).
Проверим жесткость балки , где f – максимальный прогиб.
Максимальный прогиб — жесткость не обеспечена.
Т.о. в данной задаче мы убедились в том, что не всегда сечения, подобранные из условия прочности (в данном случае – сечение из двух швеллеров) удовлетворяют условиям жесткости.
Для решения вопросов жесткости элементов требуется определять перемещения (линейные, угловые). Существуют несколько способов определения перемещений, одним из которых является определение перемещений по интегралу Мора.
Алгоритм вычисления перемещений по интегралу (формуле) Мора:
1. Составляем выражение изгибающего момента MF от действующей нагрузки.
2. Снимаем с балки (рамы, фермы и т.д.) все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу (если определяем линейное перемещение) либо единичный момент
(если определяем угловое перемещение) по направлению искомого перемещения. Составляем выражение изгибающего момента
от единичного фактора.
3. Подставляем выражения моментов в интеграл Мора:
где: Δ — перемещение в общем виде, знак Σ распространяется на все участки балки; EI – изгибная жесткость на участке.
Потенциальную энергию можно определять через работу внешних сил (см. — здесь).
В общем случае: 
δ0 – соответствующая этой силе деформация (удлинение, угол закручивания, угол поворота и тому подобное) называется обобщённым перемещением.
Под обобщённой силой Р0 следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.
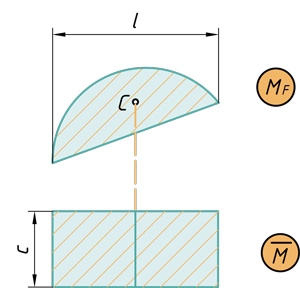
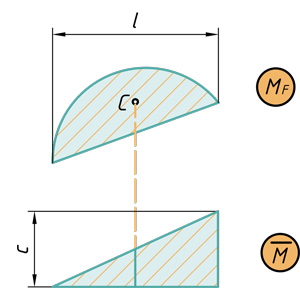
Рассмотрим общий случай нагружения при изгибе.
За отдельные обобщенные силы здесь можно принимать:
1) Сосредоточенную силу Р с реакциями 
2) Два момента М0 с соответствующими реакциями.
3) Равномерно распределённую нагрузку q с реакциями А и В.
Обобщённым перемещением δ0 будем называть величину, характеризующую деформацию, на которую нужно умножить обобщённую силу, чтобы подсчитать произведённую ею работу.
Обобщённым перемещением будут:
1) Прогиб f под силой P,

2) Взаимный угол поворота сечений, где приложены моменты М0 :
θ=θ1+θ2, или углы поворота в отдельности θ1 и θ2.
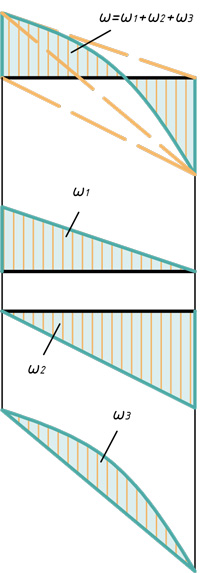
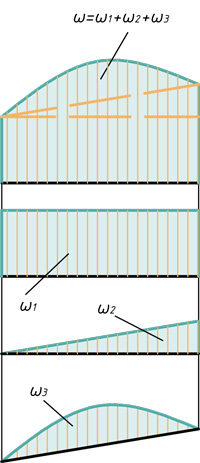
3) Площадь, заключённая между первоначальной и изогнутой осью балки в районе расположения распределённой нагрузки:
Следует отметить, что если действующая на конструкцию нагрузка представлена несколькими обобщёнными силами (Р01, P02, P03,… и т. д.),то каждое из обобщённых перемещений (δ01, δ02, δ03 и т. д.) является, вообще говоря, функцией всех обобщённых сил:

и так далее.
Так, прогиб под силой Р (см. рисунок) является результатом действия не только силы Р , но и моментов М0 и распределённой нагрузки q.
Обобщённое перемещение будем считать положительным, если соответствующая обобщённая сила на этом перемещении совершает положительную работу.
Обобщённое перемещение, соответствующее определённой обобщённой силе, не изменится при изменении способа закрепления элемента конструкции.
Зависимости 
Здесь а11, а21 и т. д. – некоторые коэффициенты пропорциональности.
Первый индекс указывает порядковый номер перемещения, второй – порядковый номер обобщённой силы.
Потенциальная энергия деформации, создающаяся в упругой системе в результате действия нескольких обобщённых сил, равна половине суммы произведений обобщённых сил на соответствующие обобщённые перемещения, получающиеся от совместного действия всех обобщённых сил:
Потенциальная энергия деформации U равна работе внешних сил W (см. — здесь).
Рассмотрим отдельные виды деформаций.
Растяжение -сжатие
Кручение
Изгиб
При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е. линейно с ними связаны и растут постепенно вместе с ними. Множитель ½ появился здесь как следствие того, что нагружение является статическим и деформации упруги – работа внешних сил измеряется площадью заштрихованного треугольника.
Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению в том сечении, где эта сила приложена.
Таким образом, в общем случае можно записать:

Под обобщённой силой Р0 следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.
Для определения перемещений при изгибе (прогибов и углов поворота сечений балок) существуют различные методы (способы). Это интеграл (формула) Мора, метод начальных параметров, метод (правило) Верещагина, формула Симпсона. Кроме них существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.
Представим, что к стержню подвешен груз. При статическом растяжении упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза (уменьшение) за счёт перемещения нижнего конца стержня полностью переходит в потенциальную энергию деформации стержня (увеличение).
Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится, и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится. Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.
Статической называется такая нагрузка, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения этих частей, т. е. их скорость остается постоянной и ускорение отсутствует. При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой.
При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере. Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу.
Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы.
Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.
Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок UF. Тогда величина UF измеряется положительной работой этих нагрузок WF, с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил W, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.
Закон сохранения энергии при деформациях упругих систем принимает вид:
UF = U
Заменяя в этой формуле величины UF и U численно равными им значениями работ WF и —W, получаем иную формулировку этого закона:
WF = —W или WF + W = 0
Эта формулировка закона сохранения энергии совпадает с так называемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю. Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии. А потенциальная энергия деформации U численно равна работе внешних сил WF, проделанной ими этой деформации:
U = WF
Для определения перемещения по формуле Симпсона необходимо:
- Построить грузовую эпюру моментов (эпюру моментов от действия всех внешних нагрузок).
- Построить единичную эпюру моментов. Для этого в сечении, где нужно определить линейное перемещение (прогиб) приложить единичную силу, а для определения углового перемещения — единичный момент, и от данного единичного фактора построить эпюру изгибающих моментов.
- Перемножить эпюры (грузовую и единичную) по формуле, которая называется формулой Симпсона:
где li – длина участка;
EIi – жесткость балки на участке;
– значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;
– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.
Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».
Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.
Во многих случаях интегрирования по Мору можно избежать и применить способ«перемножения» эпюр. Одним из таких способов является способ Симпсона, но также можно определить перемещения по способу (правилу) Верещагина. Этот способ А.К. Верещагин предложил в 1924 году, будучи студентом.
Рассмотрим последовательность действий по правилу Верещагина. Начальный этап такой же, как по формуле Мора и способу Симпсона, т.е. вначале строится грузовая эпюра от действующих нагрузок (действительное состояние), затем рассматриваем балку во вспомогательном состоянии. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила, равная единице , а если требуется найти угол поворота, то приложить следует сосредоточенную пару сил, момент, равный единице. Строится эпюра единичных моментов или эпюра от единичной нагрузки. Далее перемещение вычисляется по формуле:

Этот способ становится понятным,если доказать, что результат перемножения двух эпюр ,одна и которых произвольна ,а другая линейна, равен произведению площади грузовой эпюры на ординату единичной, взятой под центром тяжести грузовой эпюры.
Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:
- Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),
- Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.
Пусть грузовая эпюра произвольна, а единичная линейна (так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то единичная эпюра М0 оказывается ограниченной прямыми линиями). Пусть грузовая эпюра М(z) имеет криволинейное очертание, а эпюра М0 – прямолинейное (см. рисунок). Произведение
можно рассматривать как элемент
площади эпюры М, заштрихованной на рисунке.
Так как ордината М0 равна то произведение
, а весь интеграл

— статический момент площади эпюры М(z) относительно оси ординат
Но! Статический момент площади ,как известно, это произведение самой площади на координату центра тяжести. Тогда
, 
— это
ордината в единичной эпюре, расположенной под центром тяжести грузовой эпюры. Окончательно, перемещение равно:
Таким образом, результат перемножения двух эпюр равен произведению площади грузовой эпюры на ординату другой (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры.
Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс», а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».
Виды перемещений. Дифференциальное уравнение упругой линии балки
При плоском изгибе балки её упругая линия, лежащая в плоскости действия внешних сил, искривляется, точки этой линии получают некоторые перемещения.
Произвольно выбранная точка С перемещается как в направлении, перпендикулярном АВ, так и вдоль этой линии на величину . Наибольший практический интерес представляет перемещение
, которое называется прогибом балки. Угол между направлениями 1-1 и 2-2 называется углом поворота сечения балки. Таким образом , перемещения бывают линейные и угловые.
Наряду с расчётом балки на прочность необходимо производить и расчёт на жёсткость, то есть определять прогибы и углы поворота балки. Существует несколько способов решения задачи о деформациях балок. Рассмотрим аналитический способ. Установим зависимость координаты – уравнение упругой линии.
Из рисунка видно ,что
Правила знаков для перемещений, знаки перемещений
Угол считается положительным, если сечение поворачивается против хода часовой стрелки и наоборот. Прогиб считают положительным согласно принятому направлению осей координат. Если ось координат направлена вверх, то положительным будет прогиб вверх, а отрицательным — вниз.
Для нахождения зависимости y=f(z) используем известное соотношение между кривизной оси с изгибающим моментом и жесткостью сечения балки
При постоянных моменте, кривизне и жесткости балка изгибается по окружности.
Из математики известно, что кривизна кривой может быть выражена так:
Пренебрегая 
Или
При приближённом дифференциальном уравнении изогнутой оси балки пользуются принципом малости перемещений, а если перемещения очень большие, то используют точное дифференциальное уравнение. В технике допускаемая величина прогиба , где
— длина пролёта балки. Уравнение
представляет собой линейное дифференциальное уравнение второго порядка с разделяющимися переменными и может быть проинтегрировано в общем виде:
где v- линейное перемещение (прогиб), θ – угловое перемещение, С1 и С2 – постоянные интегрирования.
С1– угол поворота в начале координат, умноженной на величину ЕI;
С2 – прогиб балки в начале координат, умноженный на EI.
Значения этих постоянных определяют из граничных условий ,т.е. условий опирания балки и условий на границах смежных участков. Вот эти условия:
— у свободно лежащей балки прогибы на обеих опорах равны нулю. При симметричном нагружении у такой балки угол поворота в середине пролета также равен нулю;
— у консольной балки в заделке и прогиб и угол поворота равны нулю;
— на границе смежных участков балки прогиб и угол поворота одинаковы как для левого, так и для правого участка.
Определение перемещений по методу начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)
где у0 и φ0 – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:
Порядок определения перемещений по универсальным формулам:
- Определить все опорные реакции.
- Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
- Ось у направить вверх, ось z — вдоль балки.
- Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
- Зная начальные параметры у0 и φ0, по универсальным формулам определить интересующие нас перемещения.
При использовании универсальных формул необходимо выполнять следующие требования:
а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.
б) Каждая внешняя сила (Мi, Fi, qi) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.
Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила , а если требуется найти угол поворота, то приложить следует сосредоточенную пару
.
Далее в одном и том же произвольном сечении обоих состояний (то есть и действительного, и вспомогательного) составляются аналитические выражения изгибающего момента, которые подставляются в формулу, называемую «интегралом Мора»:
где: знак Σ распространяется на все участки балки,
а EI – изгибная жесткость на участке.
Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр. Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:
Здесь обозначено: a, b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М,
— крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния .
Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс: а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».
Следует иметь в виду, что способы «перемножения» эпюр (кроме способа Симпсона известен еще способ Верещагина) применимы только при наличии двух условий:
- Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),
- Одна из двух эпюр моментов на этом участке
должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.
При наличии нескольких участков на балке, удовлетворяющих указанным двум условиям, формула для определения перемещений принимает вид:
Если результат вычисления получается положительным, то, следовательно, направление искомого перемещения совпадает с направлением «единичного силового фактора» ( ), а если результат отрицательный, значит искомое перемещение происходит в направлении, противоположном этому фактору.
Формула Симпсона, записанная через моменты, выглядит следующим образом: перемещения (прогиб или угол поворота) равны
где li – длина участка;
EIi – жесткость балки на участке;
MF – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;
– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.
При перемножении эпюр будет полезным для определения ординат эпюр изгибающих моментов:

Задача
Определить угол поворота сечения на левой опоре φА
1) Находим опорные реакции действительного состояния 
2) Строим эпюру моментов действительного состояния М.
3) Выбираем вспомогательное состояние для определения угла поворота φА.
4) Находим опорные реакции вспомогательного состояния
«Реагируем» на знак «минус».
5) Строим эпюру моментов вспомогательного состояния:
6) «Перемножаем» эпюры
Поскольку одна из них (а именно ) линейна на всем пролете и не имеет перелома, а эпюра М тоже без перелома, то в формуле Симпсона будет всего один участок, и тогда
Знак «плюс» говорит о том, что сечение А поворачивается в сторону «единичного момента»
Метод начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)
где у0 и φ0 – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:
Порядок определения перемещений по универсальным формулам:
- Определить все опорные реакции.
- Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
- Ось у направить вверх, ось z — вдоль балки.
- Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
- Зная начальные параметры у0 и φ0, по универсальным формулам определить интересующие нас перемещения.
При использовании универсальных формул необходимо выполнять следующие требования:
а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.
б) Каждая внешняя сила (Мi, Fi, qi) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.
Задача
Найти прогиб конца консоли.
Решение
- Задаемся направлениями опорной реакции А и реактивного момента в заделке МА и составляем уравнения статики:
(1) ,
откуда А = q·2 + F = 10·2 + 20 = 40кН,
(2) ,
откуда
- Помещаем начало координат в заделку (т.0).
- Ось у направляем вверх, ось z – вдоль балки (вправо).
- Формулируем условия закрепления балки при выбранном расположении начала координат:
при z = 0: уА = 0 (1)
φА= 0 (2).
Реализуем эти условия с помощью универсальных формул:
(1): 0=ЕIу0, откуда у0=0,
(2): 0=ЕIφ0, откуда φ0=0.
- Учитывая найденные значения у0 и φ0, с помощью формулы прогибов найдём прогиб конца консоли:
при z = 4м
Знак «плюс» результата говорит о том, что прогиб конца консоли происходит в положительном направлении оси у, то есть вверх.
Для получения численного значения прогиба результат следует разделить на изгибную жёсткость балки ЕI, то есть
Как отмечалось ранее, деформацией при изгибе является искривление продольной оси балки.
Вследствие этого искривления, точки и поперечные сечения балки получают линейные и угловые перемещения.
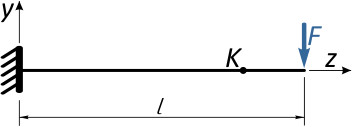
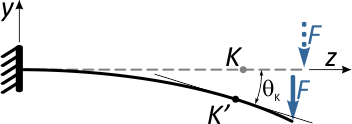
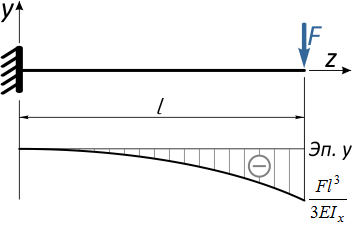
Рассмотрим на примере простой консольной балки.
Линейные перемещения
Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.
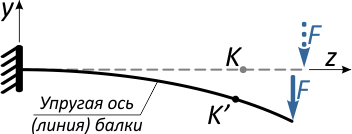
Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.
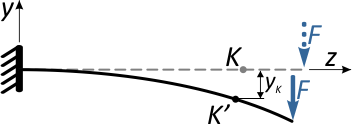
Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (yK)
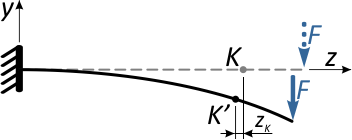
и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — zK
Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае zK<< yK), поэтому ими пренебрегают, ограничиваясь вычислением прогибов.
Линейные перемещения (прогибы балки) измеряются в метрах или кратных единицах измерения (миллиметрах и сантиметрах).
Прогибы, при которых сечение в результате деформации балки перемещается вверх принимаются положительными.
Именно по величине прогибов определяется жесткость балки.
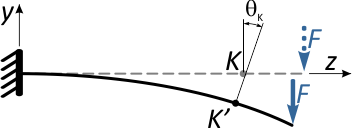
Угловые перемещения
Кроме линейных, сечения балки при изгибе получают и угловые перемещения.
Проведем касательные к продольной оси балки в точках K и K’.
В первом случае линия касательной совпадает с прямой осью балки, во втором – располагается под углом θ.
Угол между касательными очевидно равен углу между нормалями к оси балки в этих точках.
Этот угол θK называется углом наклона сечения K в результате деформации балки.
Вычисляется в радианах, с последующим переводом в градусы.
Между линейными и угловыми перемещениями при изгибе существует дифференциальная зависимость.
Например, в сечениях, углы наклона которых равны нулю следует ожидать экстремума изогнутой линии балки на данном участке.
Методы расчета перемещений
Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:
Метод начальных параметров (МНП)
Перемещения рассчитываются по уравнениям МНП
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения.
Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.
Подробнее >>
Интеграл Мора
Интеграл Мора относится к энергетическим методам расчета перемещений.
В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем.
Подробнее >>
Способ Верещагина
Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем.
Подробнее >>
Метод интегрирования дифференциального уравнения упругой линии балки
Непосредственное интегрирование дифференциального уравнения упругой линии
является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.
По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.
Эти вычисления и построения необходимы для проверки балок на жесткость.
Примеры решения задач >
Лекции по сопромату >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Прогиб стержня
при косом изгибе определяется на
основании принципа суперпозиции как
геометрическая сумма прогибов от
независимого действия прямых поперечных
изгибов
в направлении главных осей
инерции сечения. При этом искомый полный
прогиб
где u
и v
– соответственно составляющие по осям
х
и у,
вычисленные любым известным методом.
Например, перемещение
концевого сечения консольной балки
(рис. 9.5), нагруженной силой F,
будет равно

где
и
– перемещение концевого сечения
консольной балки в направлении
соответствующих осейх
и у,
определяемые, например, по способу
Верещагина; Fх
= Fcos
,
Fy
= Fsin
.
Покажем, что в
каждом сечении балки полный прогиб
перпендикулярен нейтральной линии:
,
.
(9.10)
Здесь
– угол наклона полного прогиба к оси
x.
Произведение
угловых коэффициентов полного прогиба
и нейтральной оси будет равно
.
Пример
На
двухопорную балку с консолью действует
распределенная нагрузка q
=
20 кН/м в вертикальной плоскости и сила
F
=
20 кН
в горизонтальной плоскости l
=
4 м, а
=
1 м, []
= 160 МПа,
Е
= 2105
МПа.
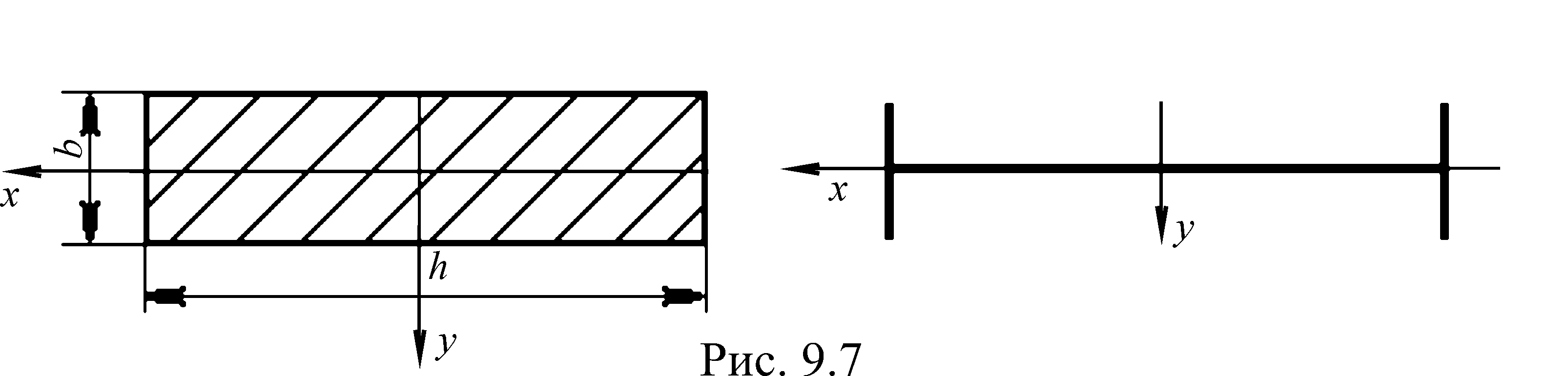
Подобрать сечение
двутавра и прямоугольника с отношением
сторон
.
Оценить отношение весов балок двутаврового
и прямоугольного сечения. Построить
эпюру напряжений, найти положение
нейтральной линии, определить перемещение
сеченияС
для балки
прямоугольного сечения.
Решение
1. Определение
реакций на опорах от сил, действующих
в вертикальной и горизонтальной
плоскостях.
,
Проверка
2. Анализ внутренних
силовых факторов от сил, действующих в
вертикальной и горизонтальной плоскостях,
построение эпюр Q
и М.
Вертикальная
плоскость
,
Горизонтальная
плоскость
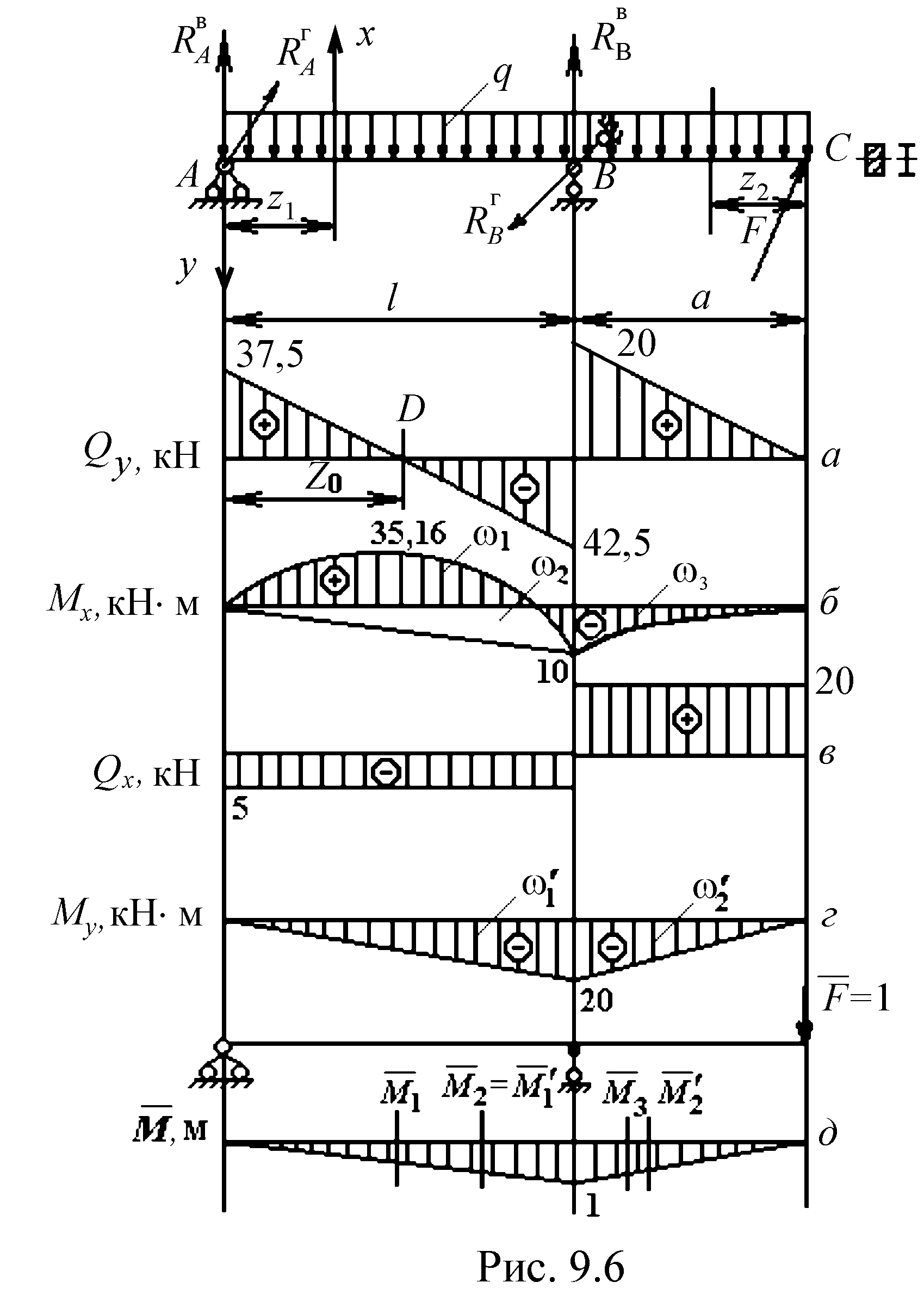
Строим эпюры
поперечных сил и изгибающих моментов
от сил, действующих в вертикальной
плоскости (рис. 9.6, а,
б) и от сил,
действующих в горизонтальной плоскости
(рис. 9.6, в,
г).
Определяем
экстремальное значение изгибающего
момента в пролете от сил, действующих
в вертикальной плоскости.
3.
Определение экстремального значения
расчетного момента.
На основании
формулы (9.8) расчетный изгибающий момент
на первом участке для прямоугольного
сечения при K
= 2 равен
,
.
Экстремальное
значение расчетного момента
.
Расчетный изгибающий
момент в сечении В:
.
Наибольший расчетный
момент имеем в пролете:
.
Для двутаврового сечения приK = 8
определяем расчетный момент в пролете:
На опоре В
Опасным
сечением для двутавра будет сечение В
с
4.
Подбор сечений из условия прочности
:
а) прямоугольное
сечение:
тогда
принимаем
б) двутавровое
сечение:
1-е приближение:
№ 45,
2-е приближение:
№ 50,
Перенапряжение
составляет
3-е приближение:
№ 55,
Недонапряжение
составляет
Принимаем двутавр
№ 50.
Определим отношение
площадей прямоугольного сечения
и
двутавра.
Из найденного
отношения следует, что значительная
рациональность двутавровых сечений по
отношению к прямоугольным, полученная
при плоском поперечном изгибе, ощутимо
снижается при косом изгибе.
6. Определим
рациональное положение балок.
Повернем сечения
балок на 90.
Для прямоугольника
,
(в пролете).
(в сечении В).
Положение сечения
на рис. 9.7 не рациональное, так как
напряжения значительно возросли.
Двутавровое
сечение:
,
(в пролете).
(в сечении В).
Положение двутавра
на рис. 9.7 не рациональное.
7. Построение эпюры
нормальных напряжений в аксонометрии
для прямоугольного сечения в опасном
сечении.
Опасное сечение
находится на расстоянии 2,375 м от опоры
А.
Определим изгибающие моменты Мх
и Му
в этом сечении.
,
8. Определение
положений силовой и нейтральной линий.
Положение силовой
линии:
Положение нейтральной
линии:
Силовая и нейтральная
линии изображены на рис. 9.8.
9. Определение
полного перемещения сечения С.
Определим перемещение
способом Верещагина в плоскости yAz
и xAz
для балки двутаврового сечения.
Эпюра вспомогательного
состояния от единичной силы изображена
на рис. 9.6, д.
Полное перемещение
сечения С.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
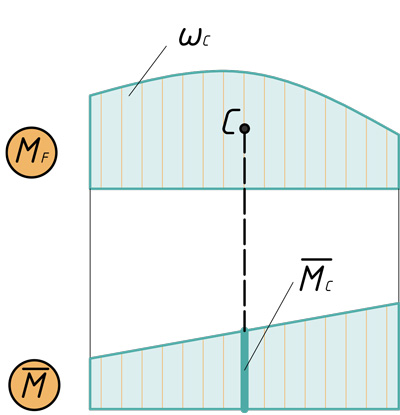
({ V={ M }_{ F } }cdot overline { M } ={ omega }_{ C }cdot { overline { M } }_{ C } )
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
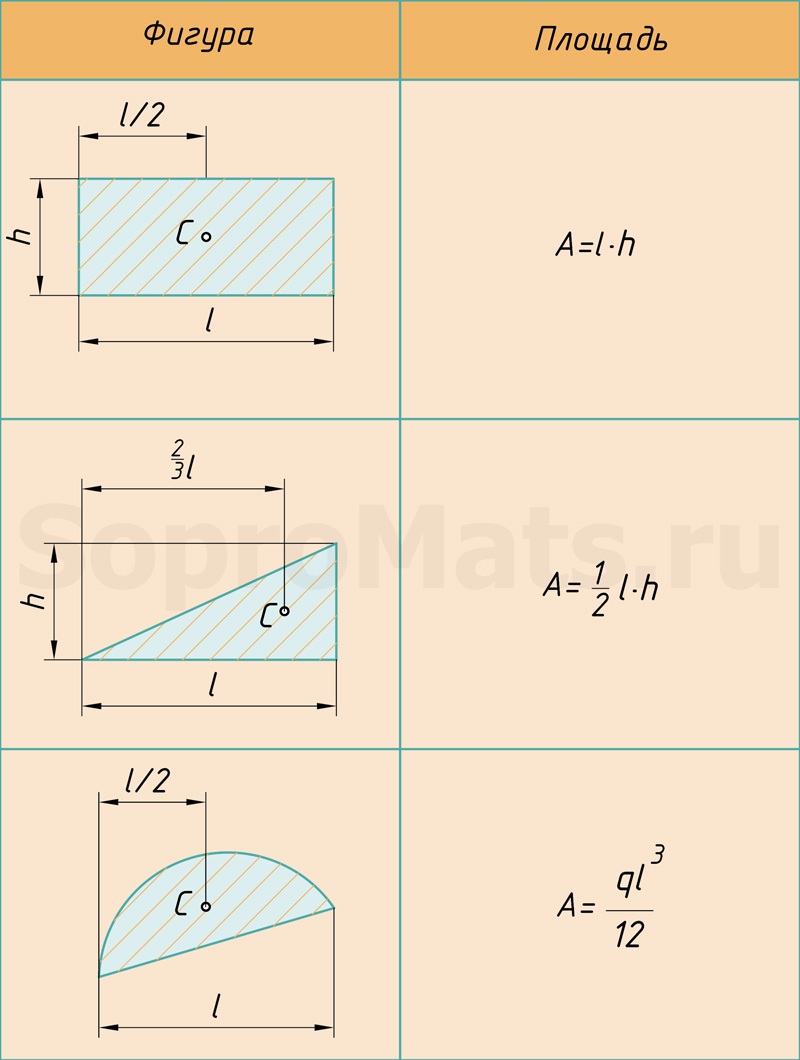
Площадь и центр тяжести эпюр
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
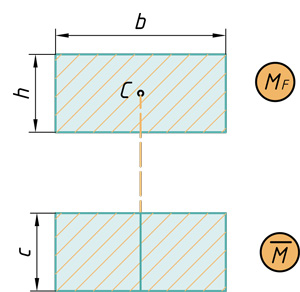
Прямоугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot c } )
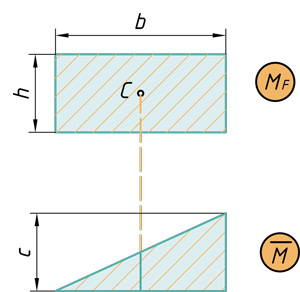
Прямоугольник на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot frac { 1 }{ 2 } cdot c } )
Треугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { 1 }{ 2 } cdot bcdot hcdot c } )
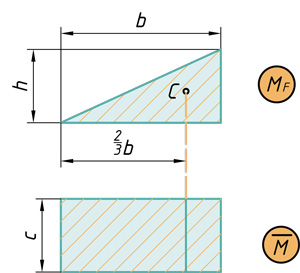
Параболический сегмент на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot c } )
Параболический сегмент на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot frac { 1 }{ 2 } cdot c } )
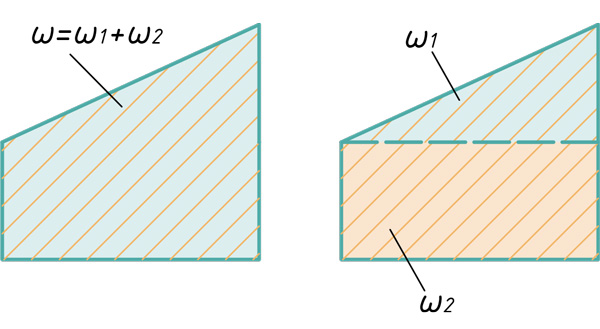
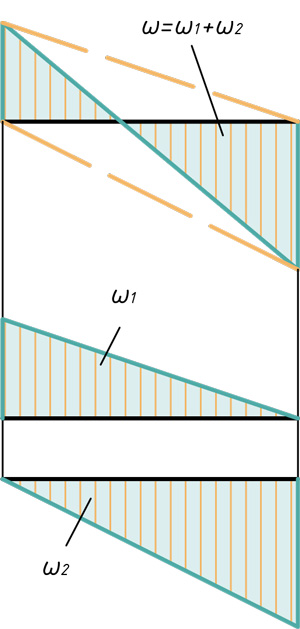
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
Прямоугольник и треугольник
Два треугольника
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
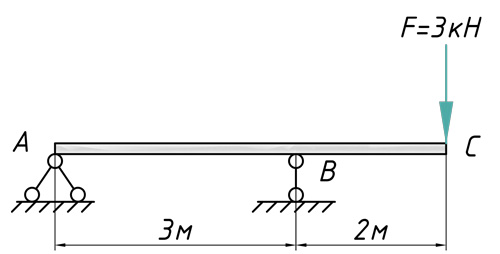
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
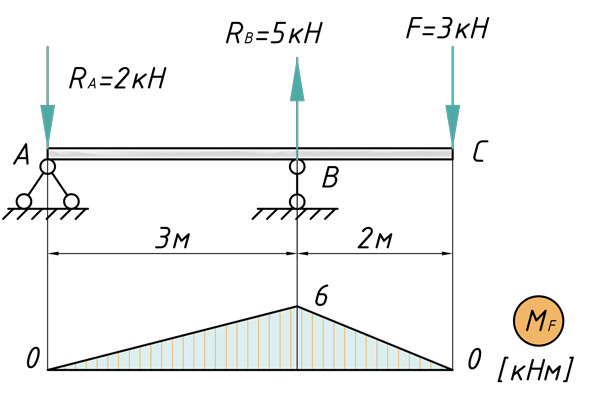
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
[ { V }_{ C }=frac { 1 }{ E{ I }_{ x } } (frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 2 }{ 3 } cdot 2+frac { 1 }{ 2 } cdot 6cdot 2cdot frac { 2 }{ 3 } cdot 2)=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } ]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
[ { V }_{ C }=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } =frac { 20cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =0.289см ]
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
[ { theta }_{ C }=frac { 1 }{ E{ I }_{ x } } (-frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 1 }{ 3 } cdot 1)=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } ]
[ { { theta } }_{ C }=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } =-frac { 3cdot { 10 }^{ 7 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =-0.0004рад ]
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
Перемещения при изгибе
Чтобы судить о работе балок, недостаточно знать только напряжения, которые возникают в ней при деформировании.
Прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной жесткости. Если балка сильно прогибается под нагрузкой, то в ней могут возникнуть колебания с большими амплитудами, приводящие к дополнительным напряжениям.
Для проверки жесткости балки необходимо уметь определять перемещения при изгибе отдельных точек ее оси.
В результате изгиба ось балки становится криволинейной. Кривизна оси балки:
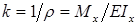
Произвольная точка, лежащая на оси балки переместится в направлении вертикальной оси y и продольной оси z. Вертикальное перемещение при изгибе будем обозначать буквой v и называть прогибом балки. Продольное перемещение при изгибе точки будем обозначать буквой u.
Касательная, проведенная к точке, расположенной на изогнутой оси балки, будет повернута по отношению к прямолинейной оси на некоторый угол 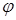
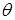
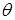
Проверка жесткости балки при изгибе сводится к требованию, согласно которому наибольший ее прогиб (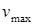
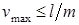
Здесь число m устанавливается нормами проектирования и колеблется обычно в пределах от 300 до 1000. Для ответственных сооружений, например, для мостов, 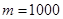
во-первых, при малых вертикальных перемещениях (прогибах v) угол наклона касательной к изогнутой оси балки и угол поворота поперечного сечения балки: 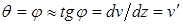
во-вторых, горизонтальным перемещением (u) можно пренебречь, так как оно по сравнению с прогибом (v) и углом поворота поперечного сечения (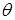
Таким образом, для определения полной картины деформации при изгибе необходимо получить уравнение оси изогнутой балки: 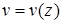
Если уравнение оси изогнутой балки известно, можно построить кривую прогибов и найти наибольший прогиб, который позволит нам судить о жесткости балки.
В ряде задач возникает необходимость и в определении угла поворота поперечного сечения.