Содержание
- 1 Введение
- 2 Алгоритм
- 2.1 Вершины и полуребра
- 2.1.1 Время работы
- 2.2 Грани
- 2.2.1 Построение графа [math]G[/math]
- 2.2.2 Маркировка граней
- 2.3 Итог
- 2.1 Вершины и полуребра
- 3 Общее время работы
- 4 См.также
- 5 Источники информации
Введение
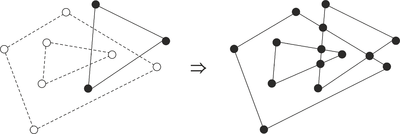
Пример работы алгоритма пересечения ППЛГ
Пересечением двух ППЛГ является ППЛГ, получающийся наложением двух исходных ППЛГ с созданием вершин в точках пересечения ребер. Определим пересечение двух ППЛГ и как ППЛГ , такой, что в нем существует грань тогда и только тогда, когда существуют грани в и в такие, что является наибольшим связным подмножеством . Иначе говоря, пересечение двух ППЛГ — это разбиение плоскости с помощью ребер из и .
| Задача: |
| Необходимо построить РСДС для , имея РСДС для и . Кроме того, для каждой грани из будем хранить ссылки на грани из и , содержащие ее. |
Алгоритм
Для начала скопируем ППЛГ и в новый РСДС. Далее необходимо преобразовать полученный РСДС, чтобы он соответствовал . Отдельно рассмотрим преобразования вершин, полуребер и граней.
Вершины и полуребра
Алгоритм заметающей прямой
Алгоритм базируется на заметающей прямой, определяющей пересечения отрезков. Запускаем алгоритм на множестве отрезков, представляющих собой ребра из и . Напомним, что алгоритм поддерживает очередь событий и текущий статус заметающей прямой. Также будем поддерживать ссылки между ребрами статуса и соответствующими полуребрами из РСДС. Поддерживаемый инвариант: в любой момент времени РСДС над заметающей прямой корректен.
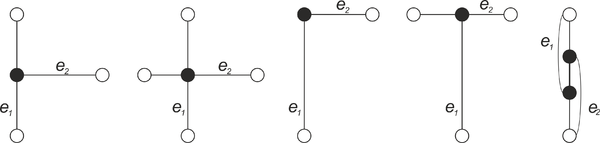
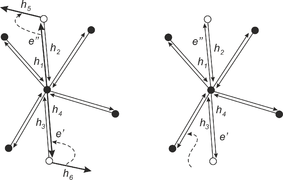
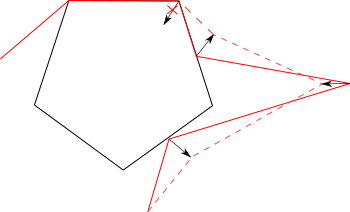
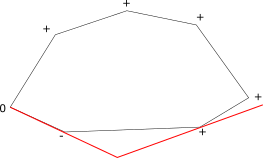
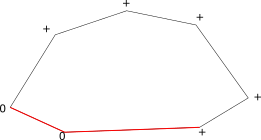
Обработка точки события происходит следующим образом: сначала обновляем и (как в алгоритме пересечения отрезков). Если оба ребра события принадлежат одному ППЛГ, переходим к следующему событию. В противном случае, необходимо модифицировать РСДС. Возможны следующие варианты пересечений (см. рисунок ниже):
- Вершина ребра проходит через ребро , разбивая его на два новых ребра.
- Ребро пересекает ребро . Образуется четыре новых ребра.
- Ребра и пересекаются в общей вершине.
- Вершина ребра проходит через ребро , разбивая его на два новых ребра.
- Ребра и имеют общий отрезок. Образуется новое ребро.
Варианты пересечений ребер и . Слева направо случаи (a) — (e).
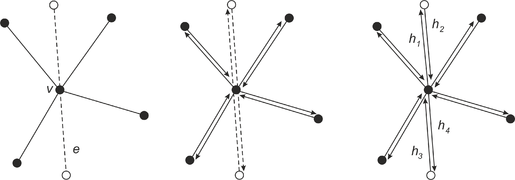
Рассмотрим один из случаев, остальные обрабатываются аналогично. Пусть ребро из проходит через вершину из . Ребро заменяем двумя ребрами и . Два полуребра, соответствующих , заменяются четырьмя полуребрами: два существующих полуребра будут исходить из концов , а два новых полуребра — из (см. рисунок). Устанавливаем ссылки на близнецов для ребер и . Обновим ссылки на следующие полуребра для и , пусть это будут и , соответственно. Не забудем установить полуребра и в качестве предыдущих полуребер у и . Теперь обновим ссылки на полуребра, инцидентные вершине . Для этого сначала при помощи порядка обхода определим, между какими полуребрами находится . Рассмотрим полуребро : свяжем его с первым полуребром, видимым из при обходе по часовой стрелке и исходящем из . Полуребро должно быть связано с первым полуребром, идущим в , при обходе против часовой стрелки. Аналогично обработаем .
|
Пересечение вершины и ребра |
|
Время работы
Большинство шагов алгоритма работают константное время. Определение соседних полуребер с и происходит за линейное время от степени вершины. Следовательно, обновление РСДС не увеличивает время работы алгоритма пересечения отрезков, поэтому сведения о вершинах и полуребрах для итогового РСДС могут быть вычислены за время , где — сумма сложностей и , — количество точек пересечения.
Грани
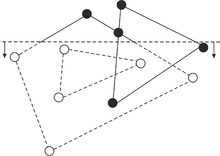
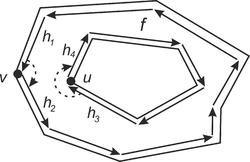
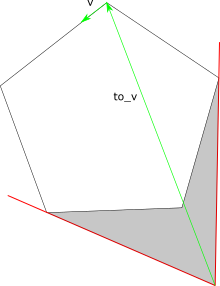
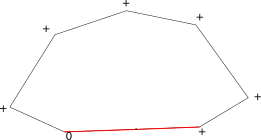
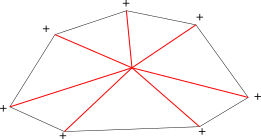
Поиск внешних границ и дырок. Вершины и – левые вершины циклов. Для полуребер и грань является внутренней, для полуребер и – внешней.
Необходимо получить информацию о гранях итогового РСДС: ссылка на полуребро внешней границы, список ссылок на полуребра дырок внутри грани, ссылка на грани из и , содержащие новую грань. Также необходимо для полуребер установить ссылки на инцидентную грань.
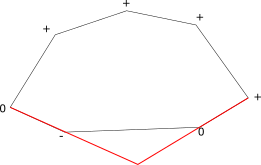
У каждой грани существует уникальная внешняя граница, поэтому количество граней будет на единицу больше, чем количество внешних границ (дополнительная граница ограничивает весь ППЛГ). Таким образом, каждой грани можно ставить в соответствие внешнюю границу данной грани (кроме внешней грани ППЛГ, для нее мы введем мнимую внешнюю границу). Следовательно, необходимо обойти все внешние границы ППЛГ и создать грань для каждой границы. Для того, чтобы определить, является цикл внешней границей или дыркой, рассмотрим самую левую вершину цикла (определяется обходом по циклу). Напомним, что полуребра ориентированы так, что инцидентная им грань лежит левее полуребра. С учетом этого, оценим угол внутри грани между полуребрами, инцидентными . Если угол меньше , то цикл является внешней границей грани, в противном случае – лежит внутри грани. Данное свойство выполняется для вершины , но может не выполняться для остальных вершин.
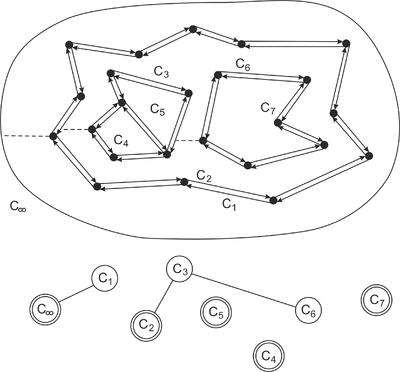
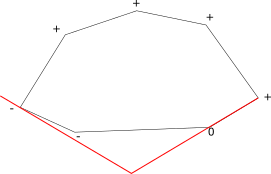
Для определения того, какие границы принадлежат одной грани, построим вспомогательный граф , в котором каждая граница является вершиной. Также добавим вершину для мнимой границы внешней грани. Между двумя вершинами графа, соответствующим двум циклам РСДС, существует ребро тогда и только тогда, когда один цикл является границей дырки, а второй цикл является ближайшим слева к самой левой вершине первого цикла. Если левее самой левой вершины цикла нет полуребер, то соединим этот цикл с мнимой границей внешней грани ППЛГ.
| Лемма: |
|
Каждой компоненте связности графа соответствует множество циклов, инцидентных только одной грани. |
| Доказательство: |
|
Рассмотрим цикл , ограничивающий дырку в грани . Грань лежит левее самой левой вершины , поэтому должен быть связан с другим циклом грани . Следовательно, циклы одной компоненты связности графа ограничивают одну и ту же грань. Покажем, что каждый цикл, ограничивающий дырку грани , находится в одной компоненте связности с внешней границей грани . Предположим, что существует цикл, для которого это не выполняется. Пусть – самый левый такой цикл, причем его левая вершина также самая левая. По определению, существует ребро между и циклом , который лежит левее . Следовательно, лежит в одной компоненте связности с , причем не является внешней границей . Получается, что лежит левее , что противоречит определению . |
Построение графа
Напомним, что в алгоритме заметающей прямой для пересечения отрезков мы искали ближайший отрезок, находящийся левее точки события. Эта информация необходима для построения графа . Сначала создадим вершину для каждой границы. Далее необходимо построить ребра в графе, для этого найдем левую вершину каждой дырки и определим, какое ребро лежит слева от данной вершины. Для эффективности будем для каждого полуребра хранить ссылку на вершину графа, содержащую это полуребро. Таким образом, информация о гранях может быть восстановлена за время , после алгоритма заметающей прямой. Также заметим, что информацию о структуре графа можно хранить в записях граней.
Маркировка граней
Необходимо для каждой грани РСДС определить, какие грани из и содержат ее. Рассмотрим вершину грани . Если является пересечением ребра из и ребра из , то по указателям на инцидентные грани можно определить, какие грани содержат данные ребра. Если является вершиной , то мы можем определить только грань из , содержащую . Необходимо научиться определять грань из , содержащую . То есть для каждой вершины из мы должны знать, какая грань из содержит данную вершину, и наоборот. Это также делается заметающей прямой.
Итог
Вход: два ППЛГ и , представленные в виде РСДС.
Выход: пересечение и , представленное в виде РСДС .
- Скопируем и в новый РСДС .
- Найдем пересечения ребер из и с помощью заметающей прямой. При обработке события будем обновлять , если событие затрагивает и . Также для вершины события сохраним информацию о ближайшем полуребре слева.
- Найдем граничные циклы в , обходя .
- Построим граф , вершинам которого соответствуют циклы, соединив ребрами дырки и циклы, ближайшие слева к левым вершинам дырок.
- Для каждой компоненты связности графа : пусть – внешняя граница компоненты связности, ограничивающая грань . Создать запись для этой грани, установить ссылку на полуребро внешней границы грани и ссылки на полуребра дырок грани. Также для всех полуребер грани установить ссылки на инцидентную грань.
- Для каждой грани из установить ссылки на грани из и , содержащие .
Общее время работы
| Теорема: |
|
Пусть имеет сложность , имеет сложность , . Пересечение и может быть построено за время , где – количество точек пересечения и . |
| Доказательство: |
| Копирование двух РСДС в один занимает времени, заметающая прямая работает времени по лемме. Создание граней работает линейное время от сложности . Маркировка граней РСДС работает за . |
См.также
- ППЛГ и РСДС (PSLG и DCEL): определение, построение РСДС множества прямых
- Пересечение множества отрезков
Источники информации
- de Berg, Cheong, van Kreveld, Overmars. Computational Geometry, Algorithms and Applicants, 2008. pp. 33-39
Быстрый поиск касательных и пересечений у выпуклых многоугольников
Время на прочтение
9 мин
Количество просмотров 7.1K
Я недавно сделал маленькую библиотеку для решения задачи поиска кратчайшего пути на 2D карте с выпуклыми препятствиями. В процессе реализации я придумал пару алгоритмов и трюков, описания которых я нигде не встречал. Поэтому делюсь этими «изобретениями» с общественностью.
Горжусь тем, что мое решение работает очень быстро. Для внушительного количества полигонов все операции можно выполнять каждый кадр. Т.е. не надо ничего запекать и вся геометрия карты может меняться в каждом кадре.
Касательные
Некоторые читатели могут возмутиться, что к полигонам, как недифференцируемым кривым, касательных нет. Но тут я использую термин не из матанализа с таким же названием. В моем случае касательная к полигону — это прямая, пересекающая его ровно в одной точке, или проходящая через сторону.
Откуда вообще эти касательные берутся? Несложными рассуждениями можно доказать, что все кратчайшие пути на карте с выпуклыми полигонами-препятствиями состоят из отрезков прямых, которые или совпадают со стороной одного из препятствия, или обоими концами являются или концом пути или касаются какого-то полигона.
Доказательство
Доказательство от противного. Допустим в кратчайшем пути какая-то часть не является прямым отрезком, или является прямым отрезком, не совпадающим со стороной полигона и один из его концов не является концом пути или касательной. У кривой всегда можно чуть-чуть срезать «угол». Ведь эта кривая не может идти по границе полигона, который состоит из прямых отрезков. Противоречие с тем, что путь кратчайший. Далее будем считать, что путь состоит из прямых отрезков.
Если же отрезок просто висит концом в пространстве или лежит на границе полигона, но не является касательной к нему, то можно этот конец чуть чуть подвинуть чтобы выпрямить угол со следующим отрезком, сократив тем самым путь. Опять противоречие.
Единственные случаи, когда мы не можем сократить путь слегка подвинув границу отрезка пути — это если отрезок уже совпадает со стороной полигона или касается его.
Все случаи выше показаны на картинке. Красным показан какой-то путь, пунктиром — сокращенный путь.
Из наблюдения выше получается следующий алгоритм построения кратчайшего пути по карте: Для всех вершин полигонов и внешних точек (возможные начала и концы путей) нужно построить касательные ко всем полигонам. Оставить только те, которые касаются обоих полигонов. Добавить к этому все границы полигонов и отрезки между внешними точками. Потом выкинуть все отрезки, которые пересекаются с каким-то препятствием. Построить граф где эти отрезки — это ребра. Найти в нем кратчайший путь.
Наивный алгоритм
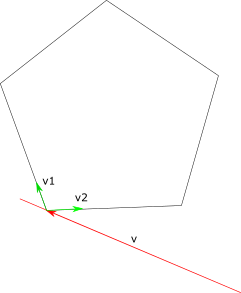
Самый простой метод построить касательные из точки — это перебрать все вершины полигона и найти те, где обе стороны лежат по одну сторону от прямой точка-вершина. Понять. что стороны лежат по одну сторону можно проверив знаки векторных произведений векторов сторон (v1, v2) и вектора из точки (v):
Получается что-то вроде такого:
// |p| хранит вершины полигона в порядке обхода против часовой стрелки.
// Класс Point используется для хранения точек или векторов.
// Оператор ^ переопределен для векторного произведения.
// Оператор - переопределен для векторной разности
std::pair<int, int> Polygon::GetTangentIds(const Point &a) {
int n = p.size();
std::pair<int, int> res = { -1, -1 };
for (int i = 0; i < n; ++i) {
if (p[i] == a) {
res = { i, i };
break;
}
Point v1 = p[i] - p[(i + n - 1) % n];
Point v = p[i] - a;
Point v2 = p[(i + 1) % n] - p[i];
double dir1 = v1 ^ v;
double dir2 = v ^ v2;
if (dir1 < eps && dir2 < -eps) {
res.first = i;
}
if (dir1 > eps && dir2 > -eps) {
res.second = i;
}
}
return res;
}Обратите внимание на сравнения с eps — так правильно сравнивать вещественные числа, чтобы ошибки округления не ломали алгоритм. Плюс или минус выбираются в зависимости от строгости сравнения. < -eps — это значит строго меньше 0, < eps — значит меньше равно. Знаки расставлены в коде выше так, чтобы выбрать самую удаленную вершину, если точка a лежит на продолжении стороны.
Этот метод работает за O(n). Можно отдельно рассмотреть случай вершины номер 0 и номер n-1, чтобы избавиться от модуля.
Быстрый логарифмический алгоритм
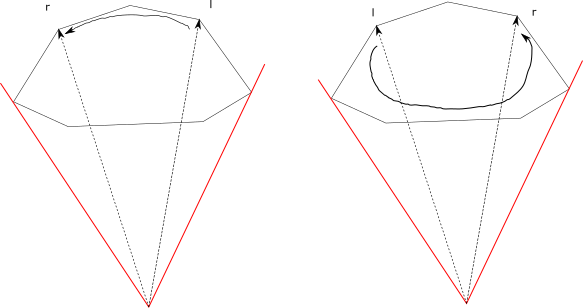
Раз уж точки уже упорядочены в порядке обхода, то тут явно напрашивается применение бинарного или хотя бы троичного поиска. Искать сразу две далекие точки одним алгоритмом не получится, поэтому будем запускать наш логарифмический поиск два раза — для левой и правой касательной.
Еще одна проблема — очень сложно даже думать о каком-то упорядоченном поиске в зацикленном контейнере. Поэтому разорвем наш полигон в первой вершине. Просто проверим, вдруг она является искомым концом касательной. Если нет, то можно забыть про сторону между последней и первой вершиной и не думать о зацикленности полигона.
Если взять произвольную сторону полигона, то можно понять, лежит ли она на «лицевой» или обратной стороне полигона. Похожим методом считается освещенность граней в компьютерной графике — достаточно посмотреть на скалярное произведение нормали к стороне и вектора из вершины. Но можно не считать нормали, а брать векторное произведение с вектором-стороной:
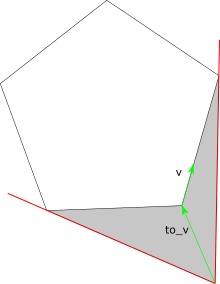
Если вектор-сторона идет слева направо относительно вектора на начало стороны, то это — лицевая сторона. В противном случае — это обратная сторона. Концы касательных — это вершины между «лицевыми» и «обратными» сторонами.
Уже можно было бы запустить бинарный поиск, если бы мы точно знали, что одна граница отрезка лежит на лицевой стороне, а другая — на обратной. Но их такие еще найти надо. Тут можно воспользоваться еще одним наблюдением — вершины внутри одной стороны строго упорядочены: лицевая сторона идет слева направо, а обратная сторона — справа налево. Если у нас есть две вершины на лицевой стороне (или обе на обратной), то мы можем легко понять, лежат ли концы касательных между них: Надо только посмотреть, лежит ли последняя вершина раньше первой в порядке вершин:
Если обе вершины на обратной стороне, то переключение между обратной и лицевой стороной происходит между ними (в порядке обхода) только если вторая вершина «перескочила» лицевую сторону и оказалась раньше первой вершины отрезка. Аналогичное правило действует для двух вершин на лицевой стороне.
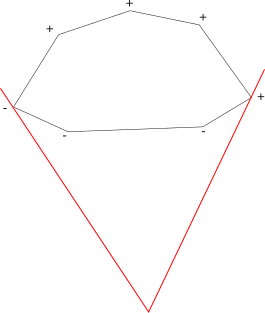
Давайте для конкретики введем «знаки» у вершин. Все вершины, сторона из которых идет справа налево относительно вектора из точки начала касательных, обозначим как «+» вершины — в них значение векторного произведения будет положительно. Все точки, сторона из которых лежит на лицевой стороне или идет слева направо относительно начала касательных, обозначим «-» — в них значение векторного произведения отрицательно.
Есть еще один неприятный случай: некоторые вершины могут иметь нулевое векторное произведение, если касательная совпадает со стороной (обозначим такие вершины «0»-вершинами). Еще более странные случаи, если точка-начало касательных лежит на стороне полигона, или вообще совпадает с вершиной. Ниже приведены все возможные случаи расположения начала касательных и «знаки» вершин:
- Касательные не совпадают ни с одной стороной.
- Левая касательная совпадает со стороной.
- Точка лежит на пересечении двух сторон.
- Правая касательная совпадает со стороной.
- Точка лежит на стороне.
- Точка совпадает с вершиной.
- Точка внутри полигона.
Нули могут быть с обоих концов от отрезка из плюсов, минусов может и не быть. Одно точно видно — плюсы есть всегда. Поэтому давайте в качестве левой касательной брать «0/-» вершину, перед которой идет «+» вершина, а в качестве правой касательной — «+» вершину, перед которой идет «0/-» вершина. Этот подход из нескольких возможных концов (при совпадении стороны и касательной) найдет самую далекую. Если же нужен самый близкий конец, то можно после выполнения логарифмического алгоритма попытаться подвинуть левый конец вперед вдоль полигона, а правый — назад. Еще, последний случай (точка внутри полигона) немного все портит. В полигоне ничего кроме «+» нет. И мы никогда не найдем границу между двумя областями. Надо аккуратно проверить, что наш поиск не повисает в этом случае и не выдает какие-то неправильные ответы.
Итак, алгоритм для левой касательной:
1. Проверить, вдруг самая первая вершина удовлетворяет условию касательной. Если это не так, то мы знаем, что переключение между "+" и "0/-" происходит (если оно вообще есть) где-то между вершинами с 0 по n-1.
2. l=0, r=n-1.
4. Пока r-l > 1:
4.1. Подсчитать "знак" вершины l.
4.2. Взять m: ceil((l+r)/2). Обратите внимание, условие 4. означает, что l < m < r.
4.3. Подсчитать знак вершины m.
4.4. Присвоить r = m, если выполняется один из трех случаев:
l - "+" и m - "-/0"
l - "+" и m - "+" и l лежит левее m
l - "-/0" и m - "/0" и l лежит правее m (или на одной прямой с ней)
4.5. Иначе присвоить l = m.Есть один нетривиальный момент, что делать, если l и m имеют одни и те же знаки лежат на одной прямой с точкой начала касательных? Т.е. вершина l не лежит ни строго левее ни строго правее m?
Это возможно только в случаях 2, 3, 6 — когда левая касательная совпадает со стороной. Если правая касательная совпадает со стороной, то знаки у вершин будут разные (дальняя — всегда +). При этом l и m указывают на 2 соседние вершины! Но, поскольку у нас поддерживается l < m, мы же разорвали цикл и ищем внутри не зацикленного массива, то это значит, что l — тот самый искомый конец касательной. Т.е. в случае, если обе вершины имеют знаки «-/0» и лежат на одной прямой, мы должны сдвинуть правый конец. Поэтому в пункте 4.4 сравнения надо делать именно так, если знаки совпадают во втором случае.
Для поиска правой касательной строгость сравнения должна быть в обратную сторону. Если обе вершины «-/0» и они лежат на одной прямой, то надо сдвинуть левую границу.
Итак, весь код алгоритма:
Код
std::pair<int, int> Polygon::GetTangentIdsLogarithmic(const Point& a) const
{
std::pair<int, int> res = { -1, -1 };
const int n = points_.size();
Point vl = points_[1] - points_[0];
Point to_l = points_[0] - a;
Point v_prev = points_[0] - points_[n - 1];
Point to_prev = points_[n - 1] - a;
double pointing_l = to_l ^ vl;
double pointing_prev = to_prev ^ v_prev;
int l = 0;
int r = n - 1;
// Проверка, что вершина 0 - левая касательная.
if (pointing_prev > eps && pointing_l < eps) {
res.first = 0;
// Случай совпадения касательной и стороны
if (pointing_l > -eps) {
Point v_next = points_[2] - points_[1];
Point to_next = points_[1] - a;
double pointing_next = to_next ^ v_next;
// точка начала еще может лежать на стороне
if (pointing_next < -eps) {
res.first = 1;
}
else if (pointing_next < eps) {
// Или совпадать с вершиной 1.
return { 1, 1 };
}
}
}
else {
// Бинарный поиск.
while (l < r - 1) {
int m = (r + l + 1) / 2;
Point vm = points_[m + 1] - points_[m];
Point to_m = points_[m] - a;
double pointing_m = to_m ^ vm;
double lm_dir = to_l ^ to_m;
if (((pointing_m < eps) || (lm_dir < -eps)) &&
((pointing_l > eps) || (lm_dir > -eps))) {
r = m;
}
else {
l = m;
to_l = to_m;
pointing_l = pointing_m;
}
}
// На случай, если |a| лежит внутри полигона, надо проверить, что бинпоиск
// остановился на ответе, а не просто на случайной вершине.
int next = (r + 1) % n;
Point to_r = points_[r] - a;
Point vr = points_[next] - points_[r];
double pointing_r = to_r ^ vr;
if (pointing_r < eps && pointing_l > eps) {
res.first = r;
// Проверка, что |a| лежит на продолжении стороны.
Point v_next = points_[(next + 1) % n] - points_[next];
Point to_next = points_[next] - a;
double pointing_next = to_next ^ v_next;
if (pointing_r > -eps) {
// Проверка, что |a| не лежит на стороне.
if (pointing_next < -eps) {
res.first = next;
}
else if (pointing_next < eps) {
// Или совпадает с вершиной.
return { next, next };
}
}
}
else return { -1, -1 };
}
// Теперь работаем с правой касательной.
vl = points_[1] - points_[0];
to_l = points_[0] - a;
v_prev = points_[0] - points_[n - 1];
to_prev = points_[n - 1] - a;
pointing_l = to_l ^ vl;
pointing_prev = to_prev ^ v_prev;
l = 0;
r = n - 1;
// Проверка первой вершины
if (pointing_prev < eps && pointing_l > eps) {
res.second = 0;
// Может ее надо подвинуть назад.
if (res.first != n - 1 && pointing_prev > -eps) {
res.second = n - 1;
}
}
else {
while (l < r - 1) {
int m = (r + l + 1) / 2;
Point vm = points_[m + 1] - points_[m];
Point to_m = points_[m] - a;
double pointing_m = to_m ^ vm;
double lm_dir = to_l ^ to_m;
if (((pointing_l < eps) || (lm_dir < eps)) &&
((pointing_m > eps) || (lm_dir > eps))) {
r = m;
}
else {
l = m;
to_l = to_m;
pointing_l = pointing_m;
}
}
// Проверка, что бинпоиск остановился на ответе.
Point to_r = points_[r] - a;
Point vr = points_[(r + 1) % n] - points_[r];
double pointing_r = to_r ^ vr;
if (pointing_r > eps && pointing_l < eps) {
res.second = r;
// Проверка, что ответ нужно подвинуть назад.
if ((res.first != l) && pointing_l > -eps) {
res.second = l;
}
}
}
return res;
}
Несмотря на длинный и, возможно, пугающий код, этот алгоритм работает быстрее наивного уже при n=4.
Проверка пересечения отрезка и полигона за O(1)
*terms and conditions apply.
Следующий трюк, которым я хотел поделиться — это как пересекать отрезок и полигон за константу, при выполнении некоторых допущений. Во-первых, ни один конец отрезка не лежит внутри полигона, и, во-вторых, касательные уже должны быть известны. В противном случае, можно за логарифм построить касательные и проверить, что концы отрезка не лежат внутри полигона. Это дало бы логарифмический алогритм проверки на пересечение.
Оба этих допущения выполняются в моей библиотеке поиска кратчайшего пути вокруг препятствий. Возможных отрезков, которые нужно проверять на пересечение — O(k*n^2), если у нас n полигонов с k вершинами. Когда как точек, из которых они торчат — всего O(k*n). Поэтому гораздо быстрее сначала проверить все точки-концы отрезков по одному разу и вычеркнуть все отрезки из плохих точек. Второе допущение выполняется, потому что все касательные на все полигоны мы и так строим — это же и есть кандидаты на ребра в графе кратчайших путей. Для проверки на пересечения они достаются бесплатно.
Итак, нам даны полигон, отрезок с концами вне полигона и касательные из одного конца отрезка. Если отрезок пересекает полигон, то он точно должен пересекать и хорду между двумя концами касательных (иначе один из его концов должен был бы лежать внутри полигона). Т.е. получается, что нужно проверить пересечение лишь с одним отрезком, а это можно сделать за O(1).
Suppose there are a number of convex polygons on a plane, perhaps a map. These polygons can bump up against each other and share an edge, but cannot overlap.
To test if two polygons P and Q overlap, first I can test each edge in P to see if it intersects with any of the edges in Q. If an intersection is found, I declare that P and Q intersect. If none intersect, I then have to test for the case that P is completely contained by Q, and vice versa. Next, there’s the case that P==Q. Finally, there’s the case that share a few edges, but not all of them. (These last two cases can probably be thought of as the same general case, but that might not be important.)
I have an algorithm that detects where two line segments intersect. If the two segments are co-linear, they are not considered to intersect for my purposes.
Have I properly enumerated the cases? Any suggestions for testing for these cases?
Note that I’m not looking to find the new convex polygon that is the intersection, I just want to know if an intersection exists. There are many well documented algorithms for finding the intersection, but I don’t need to go through all the effort.
Dandan писал(а):
Рассмотрения попарного пересечения отрезков не хватит
Тоже верно.
Dandan писал(а):
пересекает нечетном числе точек(вершина считается за две)
С этим нужно поосторожнее. Намного поосторожнее. Потому как возможны два варианта (1) луч касается ломаной внешним образом (считаем два раза); (2) пересекает ломаную (считаем один раз). Проще всего этого избежать, выбрав луч не проходящий ни через одну из точек. Благо в выборе луча мы свободны. Альтернатива (может быть и много лучшая): смотреть, находятся ли свободные концы отрезков в разных полуплоскостях. Плюс проверять на еще одну радость, лежащие на луче отрезки (их выбрасываем, но как-бы совмещаем смежные с ними).
Итого, суммарный алгорифм выглядит так: быстро проверяем вложенность многоугольника 



Еще один вопрос, требующий некоторого внимания, это возможность самопересечения ломаной (границы многоугольника). В случае, если это возможно, есть разные определения того, что значит внутри многоугольника.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
struct pt { int x, y; }; inline int area (pt a, pt b, pt c) { return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x); } inline bool intersect_1 (int a, int b, int c, int d) { if (a > b) swap (a, b); if (c > d) swap (c, d); return max(a,c) <= min(b,d); } bool intersect (pt a, pt b, pt c, pt d) { return intersect_1 (a.x, b.x, c.x, d.x) && intersect_1 (a.y, b.y, c.y, d.y) && area(a,b,c) * area(a,b,d) <= 0 && area(c,d,a) * area(c,d,b) <= 0; } |