Как найти пересечение множества прямоугольников

На собеседовании получил задачку:

Есть два прямоугольника. У каждого известны координаты левый верх и
правый низ. Нужно написать функцию, которая ответила бы на вопрос о
том, пересекаются ли эти прямоугольники.

Задачку я решил с помощью массивов и собеседование давно закончилось, но подозреваю, что решение не достаточно хорошее:

def gen_rectangle(cords):
  """Генерирует массив координат всех занимаемых прямоугольником точек"""
  rectangle = []
  for i in range(cords[0][0], cords[1][0]):
    for j in range(cords[0][1], cords[1][1]):
      rectangle.append((i, j))
  return rectangle


def intersection(cord1, cord2):
  """Есть ли пересечение"""
  rectangle1 = gen_rectangle(cord1)
  rectangle2 = gen_rectangle(cord2)
  
  for i in rectangle1:
    for j in rectangle2:
      if i == j:
        return 'We have intersection!'
  return 'All good'


cord1 = ((1, 1), (4, 8))   # первый прямоугольник
cord2 = ((3, 3), (16, 20)) # второй прямоугольник
print(intersection(cord1, cord2))

Например: если прямоугольники будут ну очень большими, то каждая занимаемая одним прямоугольником точка — это два int, такое решение не оптимально расходует память.
Как мое решение можно улучшить?

Источник

Содержание

  • 1 Определение
  • 2 Как строится?
  • 3 Как отвечать на запрос?
  • 4 Псевдокод
  • 5 Причем тут пересечение прямоугольника с множеством прямоугольников?

Определение

Priority Search Tree позволяет решать следующую задачу. Даны точек, а также запросы. Каждый запрос характеризуется отрезком по одной координате , а также числом по другой координате. Для каждого запроса структура возвращает все точки, которые находятся в отрезке по одной координате, и имеют другую координату не больше . На каждый запрос дерево отвечает за , где — количество точек в ответе.

Как строится?

Дерево строится рекурсивно. Выберем точку с наименьшей -координатой (если таких несколько, то из них выберем с наименьшим ). Все остальные точки отсортируем по и разобьем на две равные (количество может отличаться на один) части. Далее будем считать, что все точки первой части имеют координату меньше всех точек второй части (с одинаковыми поступаем как обычно — сравниваем по ). Для каждого из двух множеств, если оно не пусто, построим дерево рекурсивно.

Теорема:

PST занимает памяти.
Доказательство:
Каждая точка будет корнем ровно одного дерева. Количество деревьев не превышает количества точек. В сумме .
Теорема:

Максимальная глубина PST .
Доказательство:
При рекурсивном вызове количество точек уменьшается как минимум в два раза.
Теорема:

Построение PST работает за времени.
Доказательство:
Необходимо отсортировать точки по — для этого необходимо . Построение каждого дерева требует , где — количество точек в дереве, чтобы найти минимальную по точку, а также для построения новых списков точек для сыновей. На каждом уровне точек, уровней , значит, в сумме тоже .

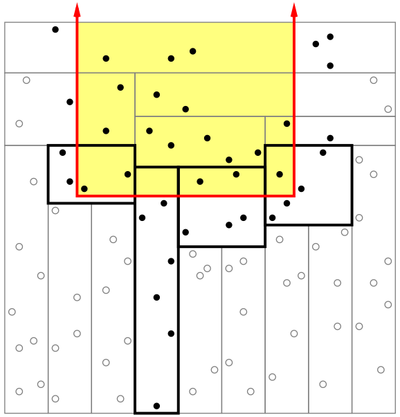
Как отвечать на запрос?

Если корня больше , то никакие точки дерева не могут быть в ответе. Будем хранить также минимальную и максимальную по точки, которые лежат в поддереве. Тогда, если отрезок запроса по не пересекается с отрезком по всех точек поддерева, то также никакие точки из дерева не должны быть добавлены в ответ. Если корень дерева лежит в нужном интервале, добавим его в ответ. Вызовем рекурсивно поиск ответа для двух сыновей.

Теорема:

Будет получен правильный ответ на запрос.
Доказательство:
Вроде бы очевидно.
Теорема:

Ответ на запрос работает за , где — размер ответа.
Доказательство:
Тут все сложнее. Представим, что мы ищем и (из запроса) в PST как в обычном дереве поиска по . Рассмотрим все точки, которые лежат между двумя путями поиска. Среди них рассмотрим точки с . Ровно эти точки и есть ответ. Разобьем все вершины на три группы. Первая — вершины, которые лежат хотя бы на одном из двух путей. Их . Вторая — вершины, которые находятся между двумя путями. Третья — все остальные. Время обработки вершин первой группы не превышает . Как только мы зашли в вершину третей группы, сразу поймем, что отрезок по не пересекается с запросом и выйдем. А зайти в них мы можем только из вершин, которые лежат на двух путях (а их ). Отлично! Зайдя в вершину второй группы, мы либо ее добавим в ответ и продолжим, либо выйдем, так как единственная причина, почему корень не подошел — его слишком большой, а, значит, и все вершины поддерева не подходят. В итоге их обработка занимает . В сумме все хорошо!

Псевдокод

 struct PST 
   point root
   point min_y, max_y
   PST *down, *up

 // pts sorted by y
 PST * build_PST(vector<point> pts)
   if (pts.size() == 0)
     return NULL
   min_y = max_ y = root = min_element(pts) // by x
   remove_element(pts, root)
   int mid = pts.size() / 2
   vector<point> down_pts = pts[0..mid]
   vector<point> up_pts = pts[mid+1..pts.size() - 1]
   down = build_PST(down_pts)
   up = build_PST(up_pts)
   if (down != NULL)
     min_y = min(min_y, down->min_y)
   if (up != NULL)
     max_y = max(max_y, up->max_y)

 void req(PST * tree, int y1, int y2, int x_max, vector<point> & ans)
   if (tree == NULL)
     return
   if (x_max < tree->root.x)
     return
   if (y1 > tree->max_y || y2 < tree->min_y)
     return
   if (tree->root in [y1..y2]x[-inf;x_max])
     answer.push_back(tree->root)
   req(tree->down, y1, y2, x_max, ans)
   req(tree->up, y1, y2, x_max, ans)

Причем тут пересечение прямоугольника с множеством прямоугольников?

PSTVIEW.png

Задача решается следующим образом. Будем находить ответ тремя разными способами, а их объединение и будет настоящим ответом. Будем считать, что объединение множеств можно делать за , где — суммарное количество элементов в них.

Первый способ. Найдем все прямоугольники, в которых прямоугольник из запроса лежит полностью. Для этого нужно решать такую задачу. Дано множество прямоугольников, для заданной точки найти все прямоугольники, в которых она лежит. Это точно можно решать за с помощью двухмерного дерева интервалов. А может можно и проще.

Второй способ. Найдем все прямоугольники, которые полностью лежат внутри заданного в запросе. Для этого воспользуемся range tree. Просто для каждого прямоугольника добавим в range tree его левый верхний угол. Задав запрос в виде нашего прямоугольника, мы получим то, что и нужно.

Третий способ. Найдем все прямоугольники, хотя бы одна сторона которого пересекает заданный в запросе. Для этого воспользуемся деревом отрезков. В структуру добавим все стороны всех прямоугольников и зададим запрос в виде нашего прямоугольника.

Утверждается, что все прямоугольники, которые нам нужны — объединение ответов, полученных тремя способами. Оценивать асимтотику всего этого мне совсем не хочется, но, наверное, это времени на запрос. памяти из-за range tree и на построение. Но, возможно, я что-то забыл или что-то можно сделать более эффективно.

Источник

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

 

Пересечения прямоугольников

Сообщение09.07.2014, 01:30 

Аватара пользователя


21/09/13
57

Подскажите как доказать, что если любые три прямоугольника из некоторого множества пересекаются, то существует точка, которая принадлежит всем им.

Профиль  

ET 

Re: Пересечения прямоугольников

Сообщение09.07.2014, 04:26 


08/05/08
593

Теорема Хелли?
Только там кажется говорится для конечного

множества «выпуклых множеств»

Профиль  

Cash 

Re: Пересечения прямоугольников

Сообщение09.07.2014, 10:36 
Заслуженный участник


12/09/10
1540

Для прямоугольников верно и в случае бесконечного их количества.

Профиль  

Skeptic 

Re: Пересечения прямоугольников

Сообщение09.07.2014, 14:25 


01/12/11
∞
1047

Это автоматически следует из понятия «пересечение».

Профиль  

Aritaborian 

Re: Пересечения прямоугольников

Сообщение09.07.2014, 17:10 

Аватара пользователя


11/06/12
10363
стихия.вздох.мюсли

Нет, не следует. Иначе зачем Хелли?

Профиль  

TopLalka 

Re: Пересечения прямоугольников

Сообщение10.07.2014, 14:42 

Аватара пользователя


21/09/13
57

Я нашел доказательства для двумерного случая и конечного количества выпуклых фигур. Подскажите как пользуясь компактностью доказать и для бесконечного случая.

Профиль  

Someone 

Re: Пересечения прямоугольников

Сообщение10.07.2014, 14:45 
Заслуженный участник
Аватара пользователя


23/07/05
17973
Москва

Подскажите как пользуясь компактностью доказать и для бесконечного случая.

Если пересечение любого конечного набора компактов из данного семейства не пусто, то…

Профиль  

TopLalka 

Re: Пересечения прямоугольников

Сообщение10.07.2014, 16:57 

Аватара пользователя


21/09/13
57

Профиль  

Skeptic 

 Re: Пересечения прямоугольников

Сообщение11.07.2014, 07:28 


01/12/11
∞
1047

Возьмём треугольник. Построим на каждой стороне треугольника с внешней стороны по прямоугольнику. Эти прямоугольники пересекаются, но не имеют общих точек, принадлежащих одновременно всем прямоугольникам.

Профиль  

TOTAL 

Re: Пересечения прямоугольников

Сообщение11.07.2014, 07:45 
Заслуженный участник
Аватара пользователя


23/08/07
5188
Нов-ск

Возьмём треугольник. Построим на каждой стороне треугольника с внешней стороны по прямоугольнику. Эти прямоугольники пересекаются, но не имеют общих точек, принадлежащих одновременно всем прямоугольникам.

Я тоже так могу:
Возьмём семиугольник. Построим на каждой стороне семиугольника с внешней стороны по прямоугольнику. Эти прямоугольники пересекаются, но не имеют общих точек, принадлежащих одновременно всем прямоугольникам

Профиль  

Cash 

 Re: Пересечения прямоугольников

Сообщение11.07.2014, 08:41 
Заслуженный участник


12/09/10
1540

Профиль  

Skeptic 

Re: Пересечения прямоугольников

Сообщение11.07.2014, 08:43 


01/12/11
∞
1047

TOTAL

, соотнесите это с постановкой задачи и попробуйте её доказать.

Профиль  

TOTAL 

Re: Пересечения прямоугольников

Сообщение11.07.2014, 08:49 
Заслуженный участник
Аватара пользователя


23/08/07
5188
Нов-ск

Прямоугольник задается двумя вершинами $(x_{ur}, y_{ur})$ и $(x_{dl}, y_{dl})$

Две вершины мало, ведь прямоугольник можно наклонять.

Профиль  

Cash 

 Re: Пересечения прямоугольников

Сообщение11.07.2014, 08:51 
Заслуженный участник


12/09/10
1540

ошибиться вроде негде…

Две вершины мало, ведь прямоугольник можно наклонять.

Ну вот оно и есть, сознание замутненное пикселями :-)

Профиль  

Skeptic 

Re: Пересечения прямоугольников

Сообщение11.07.2014, 11:19 


01/12/11
∞
1047

Задача решается при дополнительном условии: стороны прямоугольников параллельны осям координат.

Профиль  

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

I implemented it like this:

bool rectCollision(const CGRect &boundsA, const Matrix3x3 &mB, const CGRect &boundsB)
{
    float Axmin = boundsA.origin.x;
    float Axmax = Axmin + boundsA.size.width;
    float Aymin = boundsA.origin.y;
    float Aymax = Aymin + boundsA.size.height;

    float Bxmin = boundsB.origin.x;
    float Bxmax = Bxmin + boundsB.size.width;
    float Bymin = boundsB.origin.y;
    float Bymax = Bymin + boundsB.size.height;

    // find location of B corners in A space
    float B0x = mB(0,0) * Bxmin + mB(0,1) * Bymin + mB(0,2);
    float B0y = mB(1,0) * Bxmin + mB(1,1) * Bymin + mB(1,2);

    float B1x = mB(0,0) * Bxmax + mB(0,1) * Bymin + mB(0,2);
    float B1y = mB(1,0) * Bxmax + mB(1,1) * Bymin + mB(1,2);

    float B2x = mB(0,0) * Bxmin + mB(0,1) * Bymax + mB(0,2);
    float B2y = mB(1,0) * Bxmin + mB(1,1) * Bymax + mB(1,2);

    float B3x = mB(0,0) * Bxmax + mB(0,1) * Bymax + mB(0,2);
    float B3y = mB(1,0) * Bxmax + mB(1,1) * Bymax + mB(1,2);

    if(B0x<Axmin && B1x<Axmin && B2x<Axmin && B3x<Axmin)
        return false;
    if(B0x>Axmax && B1x>Axmax && B2x>Axmax && B3x>Axmax)
        return false;
    if(B0y<Aymin && B1y<Aymin && B2y<Aymin && B3y<Aymin)
        return false;
    if(B0y>Aymax && B1y>Aymax && B2y>Aymax && B3y>Aymax)
        return false;

    float det = mB(0,0)*mB(1,1) - mB(0,1)*mB(1,0);
    float dx = mB(1,2)*mB(0,1) - mB(0,2)*mB(1,1);
    float dy = mB(0,2)*mB(1,0) - mB(1,2)*mB(0,0);

    // find location of A corners in B space
    float A0x = (mB(1,1) * Axmin - mB(0,1) * Aymin + dx)/det;
    float A0y = (-mB(1,0) * Axmin + mB(0,0) * Aymin + dy)/det;

    float A1x = (mB(1,1) * Axmax - mB(0,1) * Aymin + dx)/det;
    float A1y = (-mB(1,0) * Axmax + mB(0,0) * Aymin + dy)/det;

    float A2x = (mB(1,1) * Axmin - mB(0,1) * Aymax + dx)/det;
    float A2y = (-mB(1,0) * Axmin + mB(0,0) * Aymax + dy)/det;

    float A3x = (mB(1,1) * Axmax - mB(0,1) * Aymax + dx)/det;
    float A3y = (-mB(1,0) * Axmax + mB(0,0) * Aymax + dy)/det;

    if(A0x<Bxmin && A1x<Bxmin && A2x<Bxmin && A3x<Bxmin)
        return false;
    if(A0x>Bxmax && A1x>Bxmax && A2x>Bxmax && A3x>Bxmax)
        return false;
    if(A0y<Bymin && A1y<Bymin && A2y<Bymin && A3y<Bymin)
        return false;
    if(A0y>Bymax && A1y>Bymax && A2y>Bymax && A3y>Bymax)
        return false;

    return true;
}

The matrix mB is any affine transform matrix that converts points in the B space to points in the A space. This includes simple rotation and translation, rotation plus scaling, and full affine warps, but not perspective warps.

It may not be as optimal as possible. Speed was not a huge concern. However it seems to work ok for me.

Источник

Калькулятор выполняет разбиение пересекающим прямоугольником пересекаемого. В результате разбиения может получиться от одного до четырех новых прямоугольников. В качестве результата выводятся данные таких прямоугольников в виде четырех чисел: координат левого нижнего угла прямоугольника x и y, ширины и высоты.
Обратите внимание, что получающиеся в результате прямоугольники могут накладываться или пересекаться друг с другом. То есть они НЕ являются попарно непересекающимися. Варианты таких прямоугольников приведены на картинке ниже:

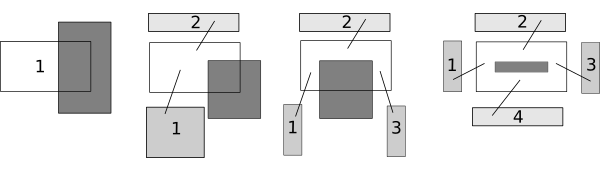
Варианты пересечения
Варианты пересечения

Это сделано специально — таким образом решается задача получения максимально возможных размеров новых прямоугольников, что полезно для некоторых алгоритмов, например, для алгоритма максимальных прямоугольников (Maximal Rectangles Algorithm1) используемого для решения задачи двумерной упаковки в контейнеры.

PLANETCALC, Пересечение прямоугольников

Пересечение прямоугольников

Пересекаемый прямоугольник

Пересекающий прямоугольник

Точность вычисления

Знаков после запятой: 2

Источник

Понравилась статья? Поделить с друзьями:
  • Как быстро найти денег в интернете
  • Как найти площадь поверхности вращения пирамиды
  • Как составить диаграмму для информационной системы
  • Как исправить sources list
  • Как найти переплату кредита