Как найти пересечение отрезка с треугольником

Пересечение линии и треугольника в 3D

У меня есть линия и треугольник где-то в трехмерном пространстве. Другими словами, у меня есть 3 точки ([x, y, z] каждая) для треугольника и две точки (также [x, y, z]) для линии.

Мне нужно найти способ, надеюсь, с помощью C ++, чтобы выяснить, пересекает ли когда-либо линия треугольник. Линия, параллельная треугольнику и имеющая более одной общей точки, должна рассматриваться как «не пересекающаяся».

Я уже сделал некоторый код, но он не работает, и я всегда получаю ложь, даже когда визуальное представление ясно показывает пересечение.

А вот и определение inside ()

Решение

1) Если вы просто хотите знать будь то линия пересекает треугольник (без пересечения):

Пусть p1, p2, p3 обозначают ваш треугольник

Выберите две точки q1, q2 на линии очень далеко в обоих направлениях.

Пусть SignedVolume (a, b, c, d) обозначает подписанный объем тетраэдра a, b, c, d.

Если SignedVolume (q1, p1, p2, p3) и SignedVolume (q2, p1, p2, p3) имеют разные знаки AND
SignedVolume (q1, q2, p1, p2), SignedVolume (q1, q2, p2, p3) и SignedVolume (q1, q2, p3, p1) имеют один и тот же знак, тогда существует пересечение.

SignedVolume (a, b, c, d) = (1/6) * точка (крест (b-a, c-a), d-a)

2) Теперь, если вы хотите пересечение, когда тест в 1) проходит

запишите уравнение прямой в параметрической форме: p (t) = q1 + t * (q2-q1)

Запишите уравнение плоскости: точка (p, N) — точка (p, p1) = 0, где N = крест (p2-p1, p3-p1)

Введите p (t) в уравнение плоскости: точка (q1 + t * (q2-q1), N-p1) = 0

Выведите t = -dot (q1, N-p1) / dot (q1, q2-q1)

Точка пересечения q1 + t * (q2-q1)

Другие решения

Чтобы найти пересечение между линией и треугольником в 3D, используйте следующий подход:

Вычислить плоскость, поддерживающую треугольник,

Пересечь линию с плоскостью, поддерживающей треугольник:

Если пересечения нет, то пересечения с треугольником нет.

Если есть пересечение, убедитесь, что точка пересечения действительно лежит в треугольнике:

• Каждое ребро треугольника вместе с нормалью плоскости, поддерживающей треугольник, определяет полупространство, ограничивающее внутреннюю часть треугольника (соответствующая ограничивающая плоскость может быть получена из вершин нормали и ребер),
• Убедитесь, что точка пересечения лежит внутри всех краевых полупространств.

Вот пример кода с подробными вычислениями, которые должны работать:

Некоторые комментарии к коду размещены с вопросом:

• Предопределенные операции ofVec3f ( .dot() а также .cross() для геометрических продуктов и т. д.) следует отдавать предпочтение при их наличии (более читабельно, избегать ошибок при реализации и т. д.
• Код вначале следует описанному выше подходу, но затем проверяет только то, что точка пересечения находится в трехмерной ограничивающей рамке отрезка отрезка [P1, P2]. Это в сочетании с возможными другими ошибками может объяснить, почему результаты неверны.
• Можно убедиться, что точка пересечения находится в трехмерном ограничивающем прямоугольнике (целого) треугольника. Хотя этого недостаточно, чтобы гарантировать пересечение, его можно использовать для того, чтобы отбирать точки, которые явно не пересекаются, и избегать дальнейших сложных вычислений.

Пересечение отрезка и треугольника

Методы, которое мы сейчас рассмотрим, также можно использовать для нахождения пересечения прямой и плоскости. Пересечения с более сложными многоугольниками можно найти путем их триангуляции.

Исходник, помещенный внизу, скорее иллюстрирует путь решения, нежели действительно эффективен.

Модель и соглашения о наименованиях обозначены на данном рисунке

Процедура, которую мы сейчас рассмотрим, будет получать на входе отрезок, заданный двумя точками, и треугольник, заданный тремя вершинами.

Решение будет состоять из следующих шагов

• Проверка: параллельна ли прямая плоскости
• Нахождение пересечения плоскости треугольника с отрезком
• Проверка: лежит ли точка пересечения на отрезке
• Проверка: лежит ли точка пересечения внутри треугольника

Точка пересечения P находится подстановкой в уравнение плоскости Ax + By + Cz + D = 0 уравнения прямой P = P₁ + мю (P₂ — P₁).

Заметим, что значения A,B,C являются компонентами вектора нормали к плоскости, который можно найти взятием векторного произведения любых двух нормализованных векторов, например

D можно затем получить, подставлив одну из вершин в уравнение плоскости, например

Это дает нам выражение для мю, из которого точка пересечения P может быть найдена через уравнение прямой.

Если знаменатель выше равен нулю, то прямая параллельна плоскости и пересечения нет. Для того, чтобы точка пересечения лежала на отрезке, мю должно принимать значения от 0 до 1.

Ну и в последнюю очередь необходимо установить, лежит ли точка пересечения внутри треугольника, ограниченного P_a, P_b, P_c.

Способ, которым мы воспользуемся, опирается на то, что сумма внутренних углов вида вершина-точка-вершина равна 2pi, если точка внутри треугольника. Для точки вне треугольника эта сумма будет меньше. Очевидно, сумма берется для одной точки — точки пересечения линии и плоскости и по всем сочетаниям вершин, как проиллюстрировано на рисунке

Если мы вычислим единичные векторы P_a1, P_a2, P_a3 как (мы проверяем точку P на принадлежность треугольнику)

Пересечение отрезка и треугольника

М етоды, которое мы сейчас рассмотрим, также можно использовать для нахождения пересечения прямой и плоскости. Пересечения с более сложными многоугольниками можно найти путем их триангуляции.

И сходник, помещенный внизу, скорее иллюстрирует путь решения, нежели действительно эффективен.

М одель и соглашения о наименованиях обозначены на данном рисунке

П роцедура, которую мы сейчас рассмотрим, будет получать на входе отрезок, заданный двумя точками, и треугольник, заданный тремя вершинами.

Р ешение будет состоять из следующих шагов

Проверка: параллельна ли прямая плоскости

Нахождение пересечения плоскости треугольника с отрезком

Проверка: лежит ли точка пересечения на отрезке

Проверка: лежит ли точка пересечения внутри треугольника

Т очка пересечения P находится подстановкой в уравнение плоскости Ax + By + Cz + D = 0 уравнения прямой P = P₁ + мю (P₂ — P₁).

З аметим, что значения A,B,C являются компонентами вектора нормали к плоскости, который можно найти взятием векторного произведения любых двух нормализованных векторов, например
(A,B,C) = (P_b — P_a) cross (P_c — P_a)

D можно затем получить, подставлив одну из вершин в уравнение плоскости, например
A P_ax + B P_ay + C P_az = -D

Э то дает нам выражение для мю, из которого точка пересечения P может быть найдена через уравнение прямой.
мю = ( D + A P_1x + B P_1y + C P_1z ) /( A (P_1x — P_2x) + B (P_1y — P_2y) + C (P_1z — P_2z) )

Е сли знаменатель выше равен нулю, то прямая параллельна плоскости и пересечения нет. Для того, чтобы точка пересечения лежала на отрезке, мю должно принимать значения от 0 до 1.

Н у и в последнюю очередь необходимо установить, лежит ли точка пересечения внутри треугольника, ограниченного P_a, P_b, P_c.

С пособ, которым мы воспользуемся, опирается на то, что сумма внутренних углов вида вершина-точка-вершина равна 2pi, если точка внутри треугольника. Для точки вне треугольника эта сумма будет меньше. Очевидно, сумма берется для одной точки — точки пересечения линии и плоскости и по всем сочетаниям вершин, как проиллюстрировано на рисунке.

Е сли мы вычислим единичные векторы P_a1, P_a2, P_a3 как (мы проверяем точку P на принадлежность треугольнику)

Построение линии пересечения двух треугольников.

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.

1. Строим проекции треугольника АВС.

2. Строим проекции треугольника EDK.

3. Находим точку пересечения стороны АС с треугольником EDK

 

4. Находим точку пересечения стороны АB с треугольником EDKи строим линию пересечения MN

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABCпроводим горизонталь CLи плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.

Строим фронтальную проекцию треугольника ABC. Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABCи строим на нем линию пересечения MN.

9. Оформление задачи.

№ вар.	ХА	YА	ZА	ХB	YB	ZB	ХC	YC	ZC	ХD	YD	ZD	ХE	YE	ZE	ХK	YK	ZK	Цена	В корзину	№ вар.
1	117	90	9	52	25	79	0	83	48	68	110	85	135	19	36	14	52	0	50 руб.	в корзину	1
2	120	90	10	50	25	80	0	85	50	70	110	85	135	20	35	15	50	0	50 руб.	в корзину	2
3	115	90	10	52	25	80	0	80	45	64	105	80	130	18	35	12	50	0	50 руб.	в корзину	3
4	120	92	10	50	20	75	0	80	46	70	115	85	135	20	32	10	50	0	50 руб.	в корзину	4
5	117	9	90	52	79	25	0	48	83	68	85	110	135	36	19	14	0	52	50 руб.	в корзину	5
6	115	7	85	50	80	25	0	50	85	70	85	110	135	20	20	15	0	50	50 руб.	в корзину	6
7	120	10	90	48	82	20	0	52	82	65	80	110	130	38	20	15	0	52	50 руб.	в корзину	7
8	116	8	88	50	78	25	0	46	80	70	85	108	135	36	20	15	0	52	50 руб.	в корзину	8
9	115	10	92	50	80	25	0	50	85	70	85	110	135	35	20	15	0	50	50 руб.	в корзину	9
10	18	10	90	83	79	25	135	48	82	67	85	110	0	36	19	121	0	52	50 руб.	в корзину	10
11	20	12	92	85	89	25	135	50	85	70	85	110	0	35	20	120	0	52	50 руб.	в корзину	11
12	15	10	85	80	80	20	130	50	80	70	80	108	0	35	20	120	0	50	50 руб.	в корзину	12
13	16	12	88	85	80	25	130	50	80	75	85	110	0	30	15	120	0	50	50 руб.	в корзину	13
14	18	12	85	85	80	25	135	50	80	70	85	110	0	35	20	120	0	50	50 руб.	в корзину	14
15	18	90	10	83	25	79	135	83	48	67	110	85	0	19	36	121	52	0	50 руб.	в корзину	15
16	18	40	75	83	117	6	135	47	38	67	20	0	0	111	48	121	78	86	50 руб.	в корзину	16
17	18	75	40	83	6	107	135	38	47	67	0	20	0	48	111	121	86	78	50 руб.	в корзину	17
18	117	75	40	52	6	107	0	38	47	135	0	20	86	48	111	15	68	78	50 руб.	в корзину	18

Начертательная геометрия решение задач

Начертательная геометрия 1 курс готовые чертежи по вариантам

Добавить комментарий

Предыстория

В 3D имеется объемная фигура с триангулированной поверхностью и требуется выяснить: находится ли некоторая данная точка внутри объема или снаружи… Вот если бы речь шла об аналитически заданной поверхности или об объединении и пересечении таких поверхностей, то всё просто — втыкаем нашу точку в аналитическую функцию поверхности f (x,y,z) = 0 и смотрим: ноль или не ноль? Если больше нуля, то точка снаружи (куда градиент показывает), а если меньше нуля, то внутри. Да и с триангулированной поверхностью тоже особой возни нет, просто чуть дольше:
— выбираем тестовую точку, которая заведомо лежит например снаружи,
— соединяем ее отрезком с некоторой данной точкой (про которую мы хотим узнать, внутри она или снаружи)
— и перебираем все треугольники, считаем пересечения: пересечений четное число — значит точка снаружи (как и тестовая, выбранная нами), нечетное — внутри.
Осталось только сообразить, как пересечения c треугольниками фиксировать. И давайте немного договоримся с терминологией: пересечением будем называть наше рабоче-крестьянское пересечение, когда отрезок уверенно пронзает треугольник, а не трусливо по-интеллигентски его всего лишь касается).

История

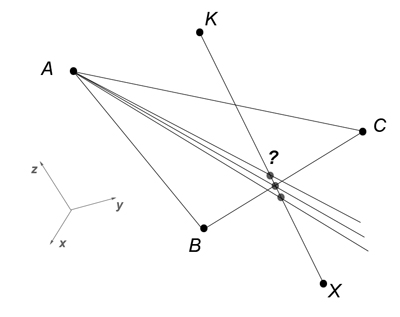
Даны: треугольник ABC и отрезок KX. Принцип у нас будет простой. Через точки A, B, C, K проведем 4 плоскости нормалями наружу и спросим у каждой, лежит ли точка X под ней или над ней. Если X лежит под всеми плоскостями, значит пересекаются наш отрезок KX и наш треугольник ABC. Ну а если нет, то извиняйте.

Алгоритм

1. Вычисляем векторы (разность векторов):
KA= A-K
KB= B-K
KC= C-K
AB= B-A
AC= C-A

2. Вычисляем смешанное произведение alpha (скалярное и векторное произведения векторов):
alpha= (KA,[ KB,KC ])

3. Вычисляем нормали плоскостей n0, n1, n2, n3 (векторное произведение векторов):
n0= [AB, AC]
n1= [KA, KB]
n2= [KB, KC]
n3= [KC, KA]

4. Ориентируем нормали наружу (умножение скаляра на вектор):
n0= -alpha*n0
n1= -alpha*n1
n2= -alpha*n2
n3= -alpha*n3

5. Вычисляем свободное слагаемое в уравнениях плоскостей (скалярное умножение векторов):
d0= -(n0, A)
d1= -(n1, K)
d2= -(n2, K)
d3= -(n3, K)

6. Вычисляем значение функции плоскостей в искомой точке X (скалярное произведение векторов плюс скаляр):
F0= (n0, X) + d0
F1= (n1, X) + d1
F2= (n2, X) + d2
F3= (n3, X) + d3

7. Анализируем (alpha, F0, F1, F2, F3):
7.0 Если alpha = 0, то точка K лежит в плоскости треугольника (внутри или снаружи треугольника -неизвестно, можно повторить алгоритм инвертировав отрезок), в любом случае отрезок не пересекается с треугольником, возможно лишь, что его концы принадлежат треугольнику. Далее рассматриваем случаи, если alpha НЕ равна нулю
7.1 Если максимум (F0, F1, F2, F3) < 0, то отрезок KX пересекается с треугольником ABC
7.2 Если максимум (F0, F1, F2, F3) > 0, то отрезок KX НЕ пересекается с треугольником ABC
7.3 Если максимум (F0, F1, F2, F3)=0, то (вот он! гадкий интеллигентский случай полукасаний и недопроникновений):
7.3.1 Если F0 =0, то X принадлежит треугольнику (лежит внутри или на ребре треугольника)
7.3.2 Если F1 или F2 или F3 = 0 то отрезок касается границы треугольника, а именно:
7.3.2.1 одна из F равна нулю, остальные — меньше нуля: отрезок пересекается с ребром
7.3.2.2 две из F равны нулю, одна — меньше нуля: отрезок содержит вершину треугольника

Послесловие

1. По поводу первоначальной задачи про 3D-поверхность. Точку K мы заведомо возьмем за пределами триангулированной поверхности, она никакому треугольнику принадлежать не будет. Далее в алгоритме введем переменную flag и будем ей присваивать значения в соответствии со случаями:
7.0 flag = 0
7.1 flag = -alpha / |alpha| (эту конструкцию назовем: «минус знак альфы», равняется она «-1» или «+1», если сама альфа не равна нулю конечно, но этот противный случай мы рассмотрели в 7.0)
7.2 flag = 0
7.3.1 flag = 0
7.3.2.1 flag = -0,5*alpha / |alpha|
7.3.2.2 flag = -0,001*alpha / |alpha|

Потом просуммируем флаги от всех треугольников и… предлагаю подумать.

2. Вместо треугольника можно взять кусочек не плоской аналитической поверхности. Тоже получается. Только у кривых аналитических поверхностей обычно бывает «задняя» сторона, это надо учесть.

Автор: FransuaMaryDelone

Источник

#include <cmath>

#include <cstdio>

#include <cstdlib>

using namespace std;

typedef struct XYZ {double x; double y; double z;};

const double M_PI = 3.14159265358979323846;

const double RTOD = 180. / M_PI;

const double EPS = 1.0E-9;

void Normalize(XYZ* p) {

  double r;

  r = sqrt(p->x * p->x + p->y * p->y + p->z * p->z);

  p->x /= r; p->y /= r; p->z /= r;

}

bool LineFacet(XYZ p1, XYZ p2, XYZ pa, XYZ pb, XYZ pc, XYZ* p) {

    double d;

    double a1, a2, a3;

    double total, denom, mu;

    XYZ n, pa1, pa2, pa3;

    n.x = (pb.y — pa.y) * (pc.z — pa.z) — (pb.z — pa.z) * (pc.y — pa.y);

    n.y = (pb.z — pa.z) * (pc.x — pa.x) — (pb.x — pa.x) * (pc.z — pa.z);

    n.z = (pb.x — pa.x) * (pc.y — pa.y) — (pb.y — pa.y) * (pc.x — pa.x);

    Normalize(&n);

    d = — n.x * pa.x — n.y * pa.y — n.z * pa.z;

    denom = n.x * (p2.x — p1.x) + n.y * (p2.y — p1.y) + n.z * (p2.z — p1.z);

    if (abs(denom) < EPS)

        return false;

    mu = — (d + n.x * p1.x + n.y * p1.y + n.z * p1.z) / denom;

    p->x = p1.x + mu * (p2.x — p1.x);

    p->y = p1.y + mu * (p2.y — p1.y);

    p->z = p1.z + mu * (p2.z — p1.z);

    if (mu < 0 || mu > 1)

        return false;

    pa1.x = pa.x — p->x;

    pa1.y = pa.y — p->y;  

    pa1.z = pa.z — p->z;  

    Normalize(&pa1);

    pa2.x = pb.x — p->x;  

    pa2.y = pb.y — p->y;  

    pa2.z = pb.z — p->z;  

    Normalize(&pa2);

    pa3.x = pc.x — p->x;  

    pa3.y = pc.y — p->y;  

    pa3.z = pc.z — p->z;  

    Normalize(&pa3);

    a1 = pa1.x * pa2.x + pa1.y * pa2.y + pa1.z * pa2.z;

    a2 = pa2.x * pa3.x + pa2.y * pa3.y + pa2.z * pa3.z;

    a3 = pa3.x * pa1.x + pa3.y * pa1.y + pa3.z * pa1.z;

    total = (acos(a1) + acos(a2) + acos(a3)) * RTOD;  

    if (abs(total — 360) > EPS)

        return false;

    return true;

}

int main() {

    //#define fp stdin

    FILE* fp = fopen(«D:\LineFacet_test.txt», «wt»);

    XYZ t1, t2, t3, p1, p2, p;

    int cnt = 0;

    while (cnt < 5) {

        t1.x = (double)rand();

        t1.y = (double)rand();

        t1.z = (double)rand();

            t2.x = (double)rand();

            t2.y = (double)rand();

            t2.z = (double)rand();

                t3.x = (double)rand();

                t3.y = (double)rand();

                t3.z = (double)rand();

        p1.x = (double)rand();

        p1.y = (double)rand();

        p1.z = (double)rand();

            p2.x = (double)rand();

            p2.y = (double)rand();

            p2.z = (double)rand();

        if (LineFacet(p1, p2, t1, t2, t3, &p)) {

            ++cnt;

            fprintf(fp, «%d:n», cnt);

            fprintf(fp, «Triangle:n»);

            fprintf(fp, «%.0lf %.0lf %.0lfn», t1.x, t1.y, t1.z);

            fprintf(fp, «%.0lf %.0lf %.0lfn», t2.x, t2.y, t2.z);

            fprintf(fp, «%.0lf %.0lf %.0lfnn», t3.x, t3.y, t3.z);

            fprintf(fp, «Line segment:n»);

            fprintf(fp, «%.0lf %.0lf %.0lfn», p1.x, p1.y, p1.z);

            fprintf(fp, «%.0lf %.0lf %.0lfnn», p2.x, p2.y, p2.z);

            fprintf(fp, «Point of intersection:n»);

            fprintf(fp, «%.2lf %.2lf %.2lfnn», p.x, p.y, p.z);

        }

    }

fclose(fp);

system(«pause»);

return 0;

}