Как найти пересечение параболы с осью абсцисс

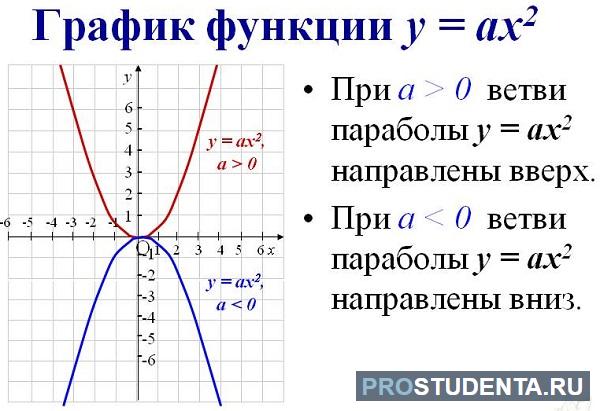
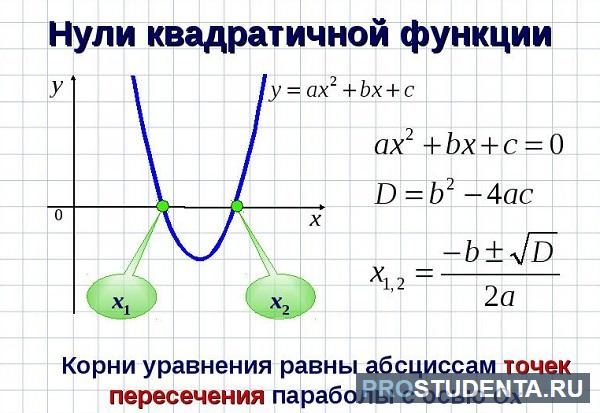
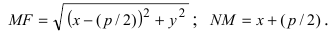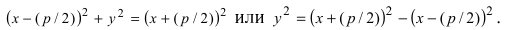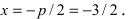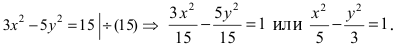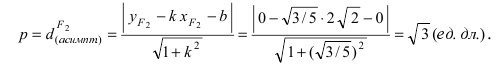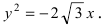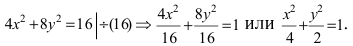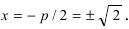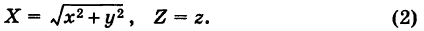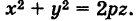Расположение графика квадратного трёхчлена относительно осей координат

В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:

$$ ax^2+bx+c = a(x+ frac{b}{2a})^2-frac{D}{4a}, D = b^2-4ac $$

Мы получаем:

• ось симметрии $x = -frac{b}{2a}$
• вершину параболы на оси симметрии $(–frac{b}{2a}; -frac{D}{4a})$
• точку пересечения (0;c) с осью OY

Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c).

Точки пересечения параболы с осью OX

Точки пересечения двух парабол

На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.

Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:

$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$

В точках пересечения выполняется равенство:

$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$

$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$

Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:

$$ Ax^2+Bx+C = 0 $$

Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).

Примеры

Пример 1. Найдите точки пересечения параболы с осями координат:

$а) y = 3x^2+2x-1$

$б) y = -4x^2-3x+1$

$в) y = 5x^2-2x+1$

$ г) y = -x^2+4x-4 $

Пример 2*. Даны две параболы

$$ y = 2x^2+5x+1 и y = x^2+3x+k $$

Найдите такое значение параметра k, чтобы параболы

1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.

По условию

$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$

$$ a_1 neq a_2, b_1 neq b_2 $$

A = 2-1 = 1, B = 5-3 = 2, C = 1-k

Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.

1) Параболы имеют две точки пересечения в двух случаях:

1 случай: $c_2 = c_1$, k = 1

2 случай: $c_2 ≠ c_1, D gt 0$

$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$

Оба случая можем объединить требованием $k gt 0$.

2) Параболы имеют одну точку пересечения, если:

$$ D = 4k = 0 Rightarrow k = 0 $$

3) Параболы не имеют общих точек, если:

$$ D = 4k lt 0 Rightarrow k lt 0 $$

Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$

Пример 3. Две параболы с общей вершиной

Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.

Пусть уравнения парабол:

$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$

Координаты вершин:

$$ left( -frac{b_1}{2a_1}, — frac{D_1}{4a_1} right), left(- frac{b_2}{2a_2},- frac{D_2}{4a_2} right) $$

По условию:

$$ {left{ begin{array}{c} -frac{b_1}{2a_1} = -frac{b_2}{2a_2} \ -frac{D_1}{4a_1} = -frac{D_2}{4a_2} end{array} right.} Rightarrow {left{ begin{array}{c} frac{b_1}{a_1} = frac{b_2}{2a_2} \ frac{D_1}{a_1} = frac{D_2}{a_2} end{array} right.} $$

Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.

Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac{x^2}{2}-3x+1$.

Координаты вершины:

$$ x_0 = — frac{b}{2a} = — frac{-3}{2 cdot frac{1}{2}} = 3, D = b^2-4ac = 3^2-4 cdot frac{1}{2} cdot 1 = 7 $$

$$ y_0 = — frac{D}{4a} = — frac{7}{4 cdot frac{1}{2}} = -3,5 $$

Уравнение искомой параболы: $y = ax^2+bx+c$

Пропорции для параметров (см. пример 3):

$$ {left{ begin{array}{c} frac{b}{a} = frac{-3}{1/2} = -6 \ frac{D}{a} = frac{7}{1/2} = 14 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = 14a end{array} right.} $$

Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:

$$ {left{ begin{array}{c} a = 1 \ b = -6a = -6 \ D = 14a = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ b^2-4ac = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ 36-4c = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ c = frac{36-14}{4} = 5,5 end{array} right.}$$

$$ y = x^2-6x+5,5 $$

$$ {left{ begin{array}{c} a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ c = — frac{1,44+2,8}{0,8} = -5,3 end{array} right.} $$

$$ y = -0,2x^2+1,2x-5,3 $$

Параболы

$$ y = frac{x^2}{2}-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$

имеют общую вершину (3;-3,5)

Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac{x^2}{3}-2x+5$.

Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.

Координаты вершины траектории кометы:

$$ x_0 = -frac{b}{2a} = -frac{-2}{2 cdot frac{1}{3}} = 3, D = b^2-4ac = 2^2-4 cdot frac{1}{3} cdot 5 = — frac{8}{3} $$

$$ y_0 = — frac{D}{4a} = — frac{-8/3}{4 cdot 1/3} = 2 $$

Уравнение траектории космического аппарата: $y = ax^2+bx+c$.

Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.

Пропорции для параметров (см. пример 3) с учетом c = 0:

$$ {left{ begin{array}{c} frac{b}{a} = frac{-2}{1/3} = -6 \ frac{D}{a} = frac{-frac{8}{3}}{frac{1}{3}} = -8 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = b^2-4a underbrace{c}_{text{= 0 }} = b^2 = -8a end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ b^2 = -8a end{array} right.} Rightarrow $$

$$ {left{ begin{array}{c} b = frac{-8a}{-6a} = frac{4}{3} \ a = -frac{b}{6} = -frac{2}{9} end{array} right.} $$

Уравнение траектории космического аппарата с «перехватом» кометы в вершине:

$$ y = -frac{2}{9} x^2+ frac{4}{3} x $$

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Оглавление:

• Что такое парабола и как она выглядит
• Каноническое уравнение параболы
• Свойства и график квадратичной функции
• Как определить, куда направлены ветви параболы
• Как найти вершину параболы по формуле
• Смещение параболы
• Как строить параболу по квадратному уравнению
• Директриса, эксцентриситет, фокус параболы
• Заключение

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

1. Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
2. Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

y² = 2 * p * x,

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x² + b x + c (узнаваемый шаблон: y = x²).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

• x₀ = -b / (2 * a);
• y₀ = y (x₀).

Пример.

Имеется функция у = 4 * x² + 16 * x – 25. Найдём вершины этой функции.

Для такой линии:

• х = -16 / (2 * 4) = -2;
• y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Получаем координаты вершины (-2, -41).

Смещение параболы

Классический случай, когда в квадратичной функции y = a x² + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0; 0).

Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Имеем: b = 2, c = 3.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 — по оси ординат.

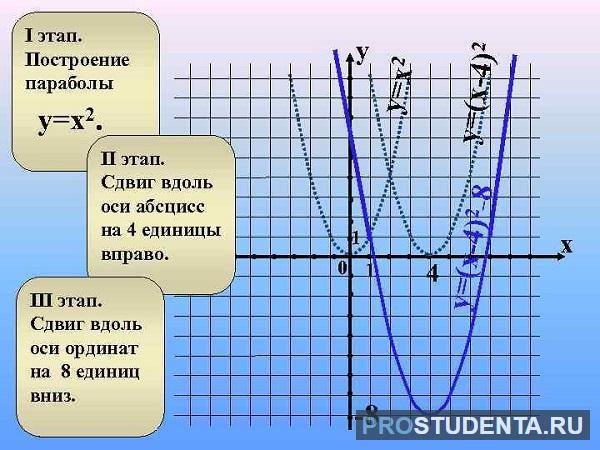
Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

Анализируя выражения и уравнения, можно увидеть следующее:

1. Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
2. Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

D = (b² — 4 * a * c).

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

• D ˃ 0, то х_{1, 2} = (-b ± D^0,5) / (2 * a);
• D = 0, то х_{1, 2} = -b / (2 * a);
• D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

• определить направление ветвей;
• найти координаты вершины;
• найти пересечение с осью ординат;
• найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х² — 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

1. а = 1, следовательно, ветви направлены вверх;
2. координаты экстремума: х = — (-5) / 2 = 5/2; y = (5/2)² — 5 * (5/2) + 4 = -15/4;
3. с осью ординат пересекается в значении у = 4;
4. найдем дискриминант: D = 25 — 16 = 9;
5. ищем корни:

• Х₁ = (5 + 3) / 2 = 4; (4, 0);
• Х₂ = (5 — 3) / 2 = 1; (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х² — 2 * х — 1 нужно построить параболу. Действуем по приведенному алгоритму:

1. а = 3, следовательно, ветви направлены вверх;
2. координаты экстремума: х = — (-2) / 2 * 3 = 1/3; y = 3 * (1/3)² — 2 * (1/3) — 1 = -4/3;
3. с осью у будет пересекаться в значении у = -1;
4. найдем дискриминант: D = 4 + 12 = 16. Значит корни:

• Х₁ = (2 + 4) / 6 = 1; (1;0);
• Х₂ = (2 — 4) / 6 = -1/3; (-1/3; 0).

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

Как найти координаты точек пересечения графика функции: примеры решения

Ирина Алексеевна Антоненко

Эксперт по предмету «Математика»

Задать вопрос автору статьи

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Пример 1

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

$5x = x- 2$;

$4x = -2$;

$x=-frac{1}{2}$

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-frac{1}{2} – 2 = — 2frac12$.

Точка пересечения будет $(-frac{1}{2};- 2frac12)$.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

Пример 2

Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Составим систему:

$begin{cases} y=2x^2-2x-1 \ y= x + 1 \ end{cases}$

Второе уравнение проще первого, поэтому подставим его вместо $y$:

$x+1 = 2x^2 – 2x-1$;

$2x^2 – 3x – 2 = 0$.

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

$x_1=2; x_2 = -frac{1}{2}$

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 — frac{1}{2} = frac{1}{2}$.

Точки пересечения будут $(2;3)$ и $(-frac{1}{2}; frac{1}{2})$.

Третий способ

«Как найти координаты точек пересечения графика функции: примеры решения» 👇

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Пример 3

Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

Парабола:

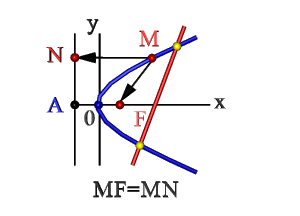
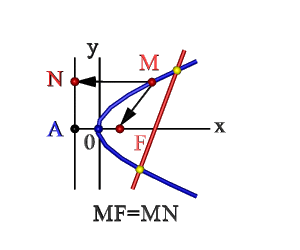
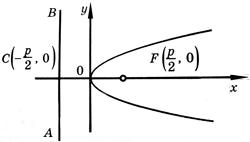
Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.

Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы

Рис. 34. Парабола, (уравнение директрисы.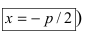

Возведем обе части уравнения в квадрат

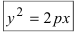
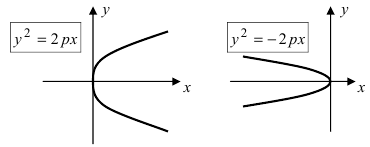
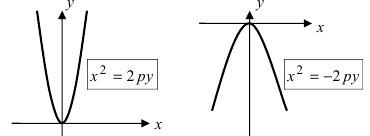
Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: (а также аналогичные ему, см. Рис. 35а и Рис. 356).

Рис. 35а. Параболы и их уравнения.

Рис. 356. Параболы и их уравнения.

Найдем координаты точек пересечения параболы с координатными осями:

Определение: Точка О(0; 0) называется вершиной параболы.

Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка 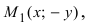следовательно, парабола симметрична относительно оси абсцисс.

Пример:

Дано уравнение параболы Определить координаты фокуса параболы и составить уравнение параболы.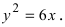

Решение:

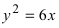
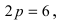
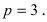
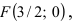
Так как из уравнения параболы следует, что следовательно, Таким образом, фокус этой параболы лежит в точке а уравнение директрисы имеет вид

Пример:

Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы 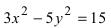до её асимптоты.

Решение:

Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.

Гипербола:

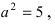
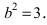
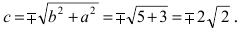
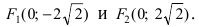
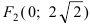
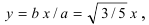
Следовательно, действительная полуось гиперболы а мнимая полуось — Гипербола вытянута вдоль оси абсцисс Ох. Определим расположение фокусов данной гиперболы Итак, Вычислим расстояние от фокуса до асимптоты которое равно параметру р:

Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:

Пример:

Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса 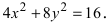Написать уравнение директрисы.

Решение:

Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:

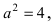
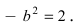
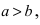
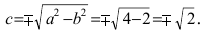
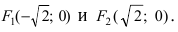
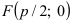
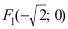
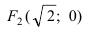
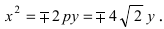
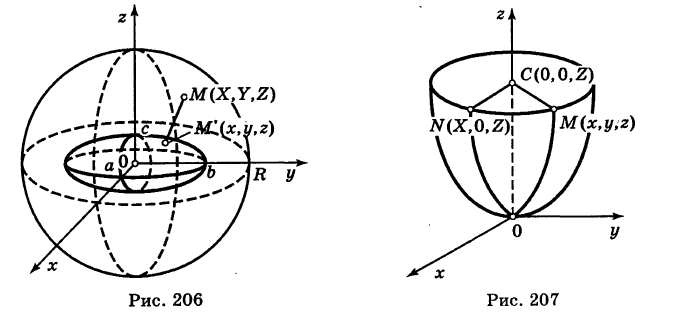
Следовательно, большая полуось эллипса а малая полуось Так как , то эллипс вытянут вдоль оси абсцисс Ох. Определим расположение фокусов данного эллипса Итак, Так как фокус параболы совпадает с одним из фокусов или эллипса, то параметр р найдем из равенства уравнение параболы имеет вид Директриса определяется уравнением

Уравнение параболоида вращения

Пусть вертикальная парабола

расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).

Для вывода уравнения поверхности рассмотрим произвольную точку 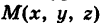параболоида вращения, и пусть эта точка получена в результате вращения точки N(X, 0, Z) данной параболы вокруг точки С(0, 0, Z).

Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем

Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения

Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.