Нахождение дополнения, суммы и пересечения подпространств
Нахождение алгебраического дополнения подпространства
Для заданного подпространства требуется найти алгебраическое дополнение подпространства
, т.е. такое подпространство
, что
.
В зависимости от способа описания подпространства , используем одно из следующих двух утверждений.
1. Если подпространство задано как линейная оболочка
столбцов матрицы
, то множество решений однородной системы
является его алгебраическим дополнением
, т.е.
(8.16)
2. Если подпространство задано как множество решений однородной системы
уравнений с
неизвестными, то линейная оболочка столбцов
транспонированной матрицы
является его алгебраическим дополнением
, т.е.
(8.17)
где — i-й столбец матрицы
.
Разумеется, в (8.16) и (8.17) указано одно из возможных алгебраических дополнений подпространства (см. свойство 3 алгебраических дополнений подпространств).
Докажем сначала справедливость (8.16) в одномерном случае , а потом в общем. Пусть
— одномерное подпространство
,
— ненулевой столбец. Найдем алгебраическое дополнение подпространства
. Рассмотрим уравнение
в координатной форме:
. Множество
решений однородной системы, состоящей из одного уравнения, образует подпространство
размерности
. Найдем пересечение
. Подставляя элемент
линейной оболочки
в уравнение
, получаем
, что возможно только при
, так как
. Следовательно, элемент
из
принадлежит подпространству
только тогда, когда
— нулевой столбец, т.е.
. Учитывая, что
, заключаем, что
— алгебраическое дополнение подпространства
в
.Таким образом,
(8.18)
Учитывая (8.18), докажем (8.16) в общем случае . Представим
в виде суммы
, где
. Из (8.15) следует, что
. Согласно (8.18), множество
решений однородной системы, состоящей из одного уравнения, дополняет
до всего пространства
. Пересечение множеств решений отдельных уравнений дает, разумеется, множество
решений системы этих уравнений. Поэтому
, что и требовалось доказать. Утверждение (8.17) доказывается аналогично, используя (8.18).
Пример 8.10. Найти алгебраическое дополнение подпространства в пространстве
многочленов не более, чем 3-й степени.
Решение. Сначала нужно переформулировать задачу для арифметического пространства (см. следствие теоремы 8.3 об изоморфизме конечномерных пространств). Для этого возьмем в стандартный базис
. Пространство
изоморфно
. Найдем координаты многочленов
и
в стандартном базисе. Раскладывая
по базису, получаем:
т.е. многочлену соответствует координатный столбец
— элемент пространства
. Аналогично получаем координатный столбец
для многочлена
.
Таким образом, исходная задача сводится к следующей: требуется найти алгебраическое дополнение подпространства в пространстве
. Используя правило (8.16), получаем, что
— это множество решений системы
, где
, т.е. системы
Решаем ее методом Гаусса. Приводим матрицу системы к упрощенному виду, прибавляя ко второй строке первую, умноженную на (-1), поделив вторую строку на 5, а затем прибавив ее, умноженную на 2, к первой:
Базисные переменные , свободные —
. Выражаем базисные переменные через свободные:
. Находим фундаментальную систему решений. Подставляя стандартные наборы свободных переменных (
и
), получаем решения:
, которые образуют фундаментальную систему решений и являются базисом алгебраического дополнения
Полученный результат переносим в пространство многочленов. По координатному столбцу
находим многочлен
Аналогично получаем . Искомое алгебраическое дополнение имеет вид
Проверим равенство . Для этого приравняем между собой линейные комбинации многочленов
и
Преобразовывая, получаем
Чтобы это равенство выполнялось тождественно, все его коэффициенты должны быть равны нулю:
Ранг матрицы этой системы равен 4 (находится, например, методом Гаусса). Поэтому однородная система имеет только нулевое решение
. Таким образом, равенство
выполняется.
Нахождение алгебраической суммы подпространств
Для заданных подпространств и
пространства
требуется найти размерность и базис их алгебраической суммы
. Рассмотрим методику решения этой задачи для двух случаев описания подпространств.
Пусть подпространства заданы линейными оболочками своих образующих (внутреннее описание): и
. Тогда, приписывая к образующим
одного подпространства образующие
другого подпространства, получаем образующие суммы подпространств
и
(8.19)
поскольку любой вектор имеет вид
. Базис суммы
можно найти как максимальную подсистему линейно независимых столбцов.
Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): и
. Тогда, переходя к внутреннему описанию, сводим задачу к предыдущему случаю, а именно нужно выполнить следующие действия:
1) для каждой однородной системы и
найти фундаментальные системы решений
и
соответственно. При этом получим
и
, где
;
2) по правилу (8.19) найти сумму .
Пример 8.11. Найти размерность и базис алгебраической суммы подпространств
, если подпространство
задано системой уравнений
подпространство — линейной оболочкой своих образующих:
Решение. Образующие подпространства были найдены в примере 8.9:
, где
. По правилу (8.19) получаем
. Найдем базис этого подпространства как максимальную линейно независимую подсистему столбцов. Составляем из этих столбцов матрицу и приводим ее методом Гаусса к ступенчатому виду:
Первый, второй и четвертый столбцы полученной матрицы линейно независимы. Значит, соответствующие столбцы исходной матрицы так же линейно независимы (так как выполнялись элементарные преобразования только над строками). Поэтому они являются базисом
и
.
Нахождение пересечения подпространств
Для заданных подпространств и
пространства
требуется найти размерность и базис их пересечения
. Рассмотрим методику решения этой задачи для двух случаев описания подпространств.
Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): и
. Тогда, приписывая к системе
, задающей одно подпространство, систему
, задающую другое подпространство, получаем систему
определяющую пересечение подпространств:
(8.20)
Базисом пересечения служит ее фундаментальная система решений.
Пусть подпространства и
пространства
заданы линейными оболочками своих образующих (внутреннее описание):
и
. Переходя от внутреннего описания подпространств к внешнему, можно свести задачу к предыдущему случаю. Однако удобнее сделать иначе. Пересечению
принадлежат только такие
, которые можно представить как равные между собой линейные комбинации столбцов
и столбцов
соответственно:
(8.21)
Представим второе равенство в (8.21) в матричном виде , где
— матрицы, составленные из данных столбцов,
— столбцы коэффициентов линейных комбинаций. Равенство
можно рассматривать как одно родную систему
уравнений с
неизвестными
и
. Каждому решению этой системы соответствует вектор
, при надлежащий пересечению
. Однако, на практике удобнее вместо системы
рассматривать однородную систему
, решения которой обладают теми же свойствами (тогда вектор
при надлежит пересечению
.
Поэтому для нахождения пересечения подпространств и
и базиса пересечения нужно выполнить следующие действия.
1. Составить блочную матрицу коэффициентов однородной системы уравнений
, где матрицы
образованы из заданных столбцов.
2. Для однородной системы с матрицей найти фундаментальную матрицу
. Матрица
имеет размеры
, где
.
3. Из первых строк матрицы
составить матрицу
. Столбцы матрицы
содержат искомые коэффициенты
линейных комбинаций (8.21).
4. Записать пересечение как линейную оболочку столбцов матрицы
.
5. Найти базис пересечения как максимальную линейно независимую подсистему образующих .
Пример 8.12. Найти размерности и базисы суммы и пересечения
подпространств
, если они заданы линейными оболочками своих образующих:
, где
Решение. Найдем базис и размерность суммы . Составим из данных столбцов блочную матрицу
Элементарными преобразованиями над строками приведем ее к ступенчатому виду:
По ступенчатому виду определяем, что первый, второй и четвертый столбцы линейно независимы. Следовательно, из 6 образующих
подпространства
максимальную линейно независимую подсистему составляют столбцы
(в этих столбцах расположен базисный минор матрицы). Следовательно, эти столбцы служат базисом суммы:
и
. По ступенчатому виду матрицы
можно также определить размерности подпространств. В блоке
две ненулевых строки, следовательно,
. Ненулевые строки блока В’ линейно независимы, следовательно,
.
Найдем базис и размерность пересечения .
1. Первый пункт алгоритма выполнен выше: матрица однородной системы
приведена к ступенчатому виду
.
2. Находим фундаментальную систему решений (используя алгоритм, описанный в разд. 5.5). Приводим матрицу системы к упрощенному виду:
Базисные переменные: ; остальные переменные — свободные. Выражаем базисные переменные через свободные:
. Придавая свободным переменным наборы значений
получаем линейно независимые решения
т.е. фундаментальная матрица имеет вид
3. Из первых трех строк матрицы
составляем матрицу
.
4. Вычисляем произведение
Столбцы этой матрицы являются образующими пересечения , где
— нулевой столбец,
.
5. Найдем базис пересечения . Для этого матрицу
приводим к ступенчатому виду
По ступенчатому виду определяем, что последние два столбца матрицы линейно независимы. Следовательно, два столбца
являются базисом пересечения
и
.
Проверим размерность пересечения подпространств, которую вычислим, используя формулу (8.13):
что совпадает с найденной ранее размерностью.
Пример 8.13. Найти размерности и базисы пересечения и суммы
подпространств
, если они заданы однородными системами уравнений:
Решение. Обозначим матрицы данных систем через и
соответственно. По правилу (8.20) пересечение
описывается однородной системой
Найдем базис пересечения — фундаментальную систему решений этой однородной системы уравнений. Составляем матрицу системы
и приводим ее к ступенчатому виду, а затем к упрощенному виду:
Базисные переменные: , свободная переменная —
. Выражаем базисные переменные через свободную:
. Фундаментальная система содержит одно решение
, которое получаем, задавая
. Следовательно,
и
.
Найдем теперь сумму . Фундаментальная система решений однородной системы
была найдена в примере 8.9. Следовательно,
, где
.
Найдем фундаментальную систему решений однородной системы . Для этого приводим матрицу системы к ступенчатому виду, а затем к упрощенному:
Базисные переменные: , свободные переменные:
. Выражаем базисные переменные через свободные:
. Фундаментальная система состоит из двух решений
, которые находим, придавая свободным переменным стандартные наборы значений (
и
). Следователь но,
и
.
По правилу (8.19) находим сумму . Чтобы определить базис, составим из столбцов
матрицу и приведем ее к ступенчатому виду:
Первые три столбца линейно независимы. Следовательно, и
.
Проверим размерность суммы подпространств. По формуле (8.13) получаем
что совпадает с найденной ранее размерностью.
Нахождение относительных алгебраических дополнений подпространств
Пусть дана цепочка подпространств . Требуется найти относительное дополнение
подпространства
до подпространства
.
Рассмотрим случай внешнего описания подпространств — как множеств решений однородных систем уравнений: и
. Согласно (8.17) базис пространства
образуют линейно независимые столбцы транспонированной матрицы
. Тогда относительное дополнение
составляют такие векторы
, которые удовлетворяют системе
. Если обозначить через
фундаментальную матрицу системы
, то линейно независимые столбцы матрицы
являются максимальной системой векторов подпространства
, линейно независимой над
, т.е. базисом относительного дополнения.
На практике нахождение базиса удобнее производить, используя ступенчатые виды матриц
и
, согласно следующей методике.
1. Привести матрицы и
при помощи элементарных преобразований строк к ступенчатому виду и удалить нулевые строки. В результате по лучим матрицы
и
модифицированного ступенчатого вида (строки каждой из этих матриц линейно независимые).
2. Найти фундаментальную матрицу однородной системы уравнений
.
3. Вычислить матрицу . Ее столбцы образуют искомый базис
.
Рассмотрим случай внутреннего описания подпространства как линейной оболочки своих образующих:
. Согласно (8.16) множество решений системы уравнений
(матрица
составлена из образующих) является алгебраическим дополнением
. Тогда множество решений системы
является относительным дополнением
, а ее фундаментальная система решений — базисом относительного дополнения.
Замечание 8.10. Способы описания подпространств комплексного линейного пространства, а также методы решения типовых задач аналогичны рассмотренным. В отличие от вещественного арифметического пространства вместо операции транспонирования матрицы в комплексном арифметическом пространстве
нужно использовать операцию сопряжения матрицы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пусть
заданы два подпространства R1
и R2
n-мерного
пространства R.
Определение:
Если каждый вектор x
пространства R
можно, и притом единственным образом,
представить как сумму двух векторов:
x
=
x1
+
x2,
где
, то говорят, что пространство R
разложено в прямую сумму подпространств
R1
и R2.
Это записывают так:
R
= R1
+ R2,
Теорема. Для
того, чтобы пространствоR
разлагалось в прямую сумму подпространств
R1
и R2,достаточно,
чтобы:
-
Подпространства
R1
и R2
имели только один общий вектор x
=
0 (нулевой вектор). -
Сума
размерностей этих подпространств была
равна размерности пространства R.
Пусть
имеем два произвольных подпространства
R1
и R2
линейного пространства R.
Подпространство пересечения
R1
и R2
— это совокупность векторов, принадлежащих
обоим подпространствам R1
и R2:
☺ Пример
124. Пусть
R1
и R2
– два двумерных подпространства
трехмерного прос-транства (две плоскости,
проходящие через начало координат).
Тогда их пересечение
есть одномерное подпространство (прямая,
по которой эти плоскости пересекаются).
По
двум подпространствам
R1
и R2
можно построить еще одно подпространство,
которое называют суммой:
векторами этого подпространства являются
всевозможные суммы вида:
x
=
x1
+
x2, (*)
где
,
его обозначают:
(в
отличие от прямой суммы двух подпрос-транств,
запись (*) элемента из R
может быть неоднозначной. Легко проверить,
что построенные элементы (*) образуют
подпространство.
Теорема. Сумма
размерностей
R1
и R2,
равна размерности их суммы плюс
размерность пересечения.
☺ Пример
125. Найдем
базис пересечения подпространств
, если R1
натянут на векторы a1
и
a2,
а R2
– на векторы b1
и
b2:
,
,
,
.
Решение:
Нетрудно заметить, что векторы a1
и
a2,
b1
и
b2:
— линейно независимы. Согласно
вышеприведенной теореме запишем
размерность пересечения
в виде d
= k+r-s,
где k
= 2 – число независимых векторов,
порождающих подпространство R1;
r
= 2 – число независи-мых векторов,
порождающих подпространство R2;
s
– число независимых векторов, порождающих
подпространство
(его предстоим вычислить).
Применяя
один из способов вычисления ранга
системы векторов, получаем: s
= 3. В таком случае размерность пересечения
d
= 2 + 2 — 3 = 1/
Найдем базис из
условия:
c
= x1
a1+
x2
a2 =
x3
b1+
x4
b2
или
Решая
эту систему одним из способов, изложенных
в Гл.5, получим: x1
=
-s;
x2
=
4s;
x3
=
-3s;
x4
=
s,
где s
– произвольная постоянная. Принимая
s
= -1, получим:
c
= a1—
4 a2
= 3
b1—
b2
= (5, -2, -3, -4).
Ответ:
базис пересечения подпространств: c
=
a1—
4
a2
=
3
b1—
b2
= (5, -2, -3, -4).
☻Решите
примеры:
Пример
126. Найдем
базис пересечения подпространств
, если R1
натянут на векторы a1
и
a2,
а R2
– на векторы b1
и
b2:
,
,
,
.
Ответ:
базис пересечения подпространств: c
=
-4a1
+
13a2
=
8 b1+
3b2
= (5, 9, -13, 27).
Пример
127. Найдем
базис пересечения подпространств
, если R1
натянут на векторы a1
и
a2,
а R2
– на векторы b1
и
b2:
,
,
,
.
Ответ:
базис пересечения подпространств: c
=
2a1—
3
a2
=
—
b1+
b2
= (1, 3, -1, 1).
Соседние файлы в папке СРС
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Теория функций действительного переменного
- Эквивалентные множества
- Счётные множества
- Метрическое пространство
- Множества в метрическом пространстве
- Сходимость метрического пространства
- Непрерывные отображения метрического пространства
- Полные метрические пространства
- Принцип сжимающихся отображений
- Применение принципа сжимающихся отображений
- Линейные пространства
- Линейные функционалы
- Выпуклые множества и функционалы
- Нормированные и евклидовы пространства
- Непрерывные линейные функционалы
- Сопряжённое пространство
- Слабая сходимость
- Обобщённые функции
- Линейные операторы
- Компактные операторы
- Системы множеств
- Мера множеств, измеримые функции
- Интеграл Лебега
- Теория дифференцирования
- Пространства суммируемых функций
- Тригонометрические ряды
- Ортогональные системы функций
- Преобразование Фурье
Введение на некотором множестве метрики (то есть расстояния между элементами этого множества) позволяет ввести понятие сходимости — фундаментальное понятие математического анализа.
В данном разделе мы рассмотрим такие множества, в которых можно ввести фундаментальные понятия алгебры: линейная комбинация, линейная зависимость, базис.
Понятие линейной комбинации, в свою очередь, позволяет говорить о выпуклых множествах и телах — аналогах привычных понятий из геометрии.
Определение[править]
Непустое множество 
В зависимости от того, какие числа используются для построения линейного пространства, различают действительные и комплексные линейные пространства. Можно также рассматривать линейные пространства, построенные над произвольным полем.
Элементы линейного пространства часто называют векторами.
Два линейных пространства 

,
,
и установлены следующие взаимные соответствия
,
то для любого числа 
,
.
Примеры[править]
Примером линейного пространства, является пространство геометрических радиусов-векторов на плоскости L = R2 = { x = x1·i + x2· j}:
x = x1·i + x2· j, y = y1·i + y2· j,
x + y = (x1+ y1)·i + ( x2+ y2)· j, α·x = (αx1)·i + (αx2)· j,
0 = 0·i + 0· j, −x = (−x1)·i +(−x2)· j.
Справедливость остальных аксиом линейного пространства следует из свойств операций сложения и умножения на число действительных чисел.
Линейная зависимость[править]
Система элементов
линейного пространства 
,
не все равные нулю, что имеет место равенство
.
Если же это равенство возможно только при
,
то система векторов называется линейно независимой.
Бесконечная система элементов называется линейно независимой, если любая её конечная подсистема является линейно независимой.
Если в линейном пространстве 




Базисом в n-мерном линейном пространстве называется любая система n линейно независимых элементов.
Конечномерные линейные пространства являются основным предметом изучения линейной алгебры, в анализе же, как правило, рассматриваются бесконечномерные линейные пространства.
Подпространства[править]
Непустое подмножество 


Другими словами, 



.
Любое пространство можно считать своим подпространством. Кроме того, любое пространство содержит подпространство состоящее из одного — нулевого — элемента (так называемое нулевое подпространство). Подпространство, отличное от всего пространства и содержащее хотя бы один ненулевой элемент, называется собственным.
Пересечение двух подпространств 




.
По определению пересечения множеств:
,
.
Следовательно, по определению подпространства линейного пространства:
,
.
Так как вектор 


.
Утверждение доказано.
По индукции можно доказать, что пересечение любого количества подпространств является подпространством.
Пусть 




.
Покажем, что линейная оболочка множества существует. Рассмотрим систему всех подпространств, содержащих множество 


Линейно-независимая система 


Фактор-пространства[править]
Пусть 



.
Легко проверить, что это отношение действительно удовлетворяет аксиомам отношения эквивалентности: рефлексивности, симметричности и транзитивности.
Рефлексивность:
,
так как любое подпространство содержит нулевой элемент, то любой элемент эквивалентен сам себе в указанном смысле.
Симметричность. Рассмотрим два вектора 
,
тогда:
,
так как 
Транзитивность. Рассмотрим три вектора 
,
,
тогда, по определению подпространства линейного пространства:
,
с другой стороны
,
а значит
.
Классы эквивалентности построенного отношения называются классами смежности(по подпространству 



В любом фактор-пространстве можно естественным образом ввести операции сложения и умножения на число. Рассмотрим два класса смежности : 
Выберем в каждом из этих классов по одному представителю
и назовём суммой этих классов тот класс, которому принадлежит элемент 
Аналогичным образом определяется и произведение класса на число — класс, которому принадлежит произведение представителя на класса на то это число.
Можно проверить, что определение сложения и умножения на число в фактор-пространстве не зависит от выбора представителей классов. Введённые таким образом операции удовлетворяют аксиомам линейного пространства, а значит фактор-пространство линейного пространства само является линейным пространством, причём нулевым элементом фактор-пространства является подпространство 
Упражнение 1. Докажите, что введённые операции действительно удовлетворяют аксиомам линейного пространства и не зависят от выбора представителей классов смежности.
Размерность фактор-пространства 


Если коразмерность некоторого подпространства 




,
где 

Упражнение 2. Докажите это утверждение.
Упражнение 3. Докажите, что если размерность пространства 




Решения для упражнений[править]
Упражнение 1.
Пусть 
Докажем, что сумма классов не зависит от выбора представителей.
Возьмём в каждом классе по два представителя:
,
.
Рассмотрим следующие вектора:
,
и найдём разность между ними
.
По определению класса смежности
,
.
А так как 
.
Таким образом, элементы 

Докажем, что определение умножения класса смежности на число не зависит от выбора представителя.
Пусть дан класс смежности 

Выберем двух представителей класса
.
Нужно доказать, что вектора
принадлежат одному классу смежности.
Вычислим их разность:
.
По определению класса смежности
,
но так как 
.
Таким образом, определение операции умножения класса смежности на число не зависит от выбора представителя.
Докажем теперь, что для фактор-пространства с указанными операциями выполняются свойства линейного пространства.
Начнём с того, что укажем нулевой элемент фактор-пространства.
Нулевым элементом фактор-пространства является подпространство 
Для доказательства этого факта нужно показать, что для любого класса смежности 
.
Это равенство означает, что существуют такие вектора 

или
,
но так как 
,
а следоватльно они принадлежат одному классу смежности,
а класс 
Для доказательства остальных свойств нужно использовать тот факт, что определение суммы классов смежности и умножения класса смежности на число не зависит от выбора представителя, а представители классов смежности являются элементами линейного пространства.
Упражнение 2.
Пусть фактор пространство 

тогда произвольный класс можно представить в виде линейной комбинации
.
Рассмотрим вектор 


,
то есть любой вектор 
,
причём
.
Упражнение 3.
Если 

Будем далее считать, что 
Пусть 

Так как размерность пространства 


была линейно независимой.
Вектора 

Действительно, если 

,
или
,
где 
то есть система окажется линейно-зависимой.
Аналогично доказывается, что 
Так как мы указали 


Рассмотрим теперь произвольный класс смежности 

Так как система
является линейно-независимой, то вектор 
.
Так как
,
то вектор 
,
а так как класс смежности вполне определяется одним своим представителем, то
.
Утверждение доказано.
Подпространство линейного пространства
Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λx∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Сумма и пересечение подпространств
Пусть L и M — два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис 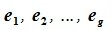
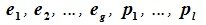
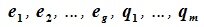
|
|
(6.1) |
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
|
|
(6.2) |
Тогда
|
|
(6.3) |
Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
|
|
(6.5) |
Из уравнений (6.4) и (6.5) имеем:
|
|
(6.6) |
или
|
|
(6.7) |
Но векторы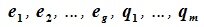
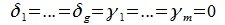
|
|
(6.8) |
В силу линейной независимости базиса подпространства L имеем:
|
|
(6.9) |
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
|
|
(6.10) |
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов 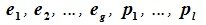
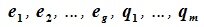
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Прямая сумма подпространств
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис 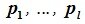
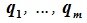
|
|
(6.11) |
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
|
|
(6.12) |
или
|
|
(6.13) |
Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M=0, то
|
|
(6.14) |
Но векторы 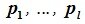
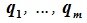
|
|
(6.15) |
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
|
|
(6.16) |
Из (6.16) имеем:
|
|
(6.17) |
|
|
(6.18) |
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
|
|
(6.19) |
Вычитая (6.19) из (6.17), получим
или
|
|
(6.20) |
Так как 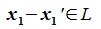
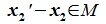
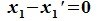
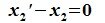
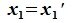
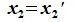
Содержание
Пересечение и сумма подпространств
проверено. нафиг тогда определение 1, если есть 1′?
Пересечение и сумма
Внутренняя прямая сумма
Определение 2. Пространство 




Прямая сумма векторных пространств обозначается через 
Замечание 2. Определенная таким образом прямая сумма называется внутренней.
Пример 2. Пусть 




Предложение 3. Сумма 
-
для
,
-
.
Следствие 1. Если 


Предложение 4. Для любого 






Определение 3. Для подпространства 




Внешняя прямая сумма
Литература
Наверх
























































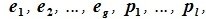
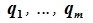
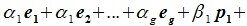
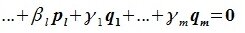
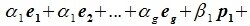

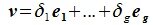
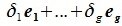
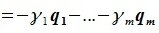
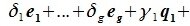
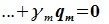
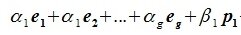
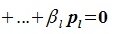
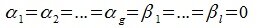
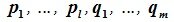
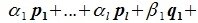
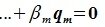
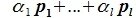
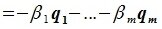

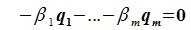
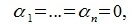
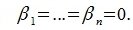
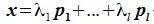
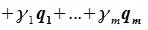
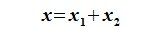
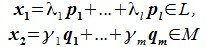
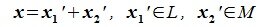
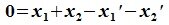
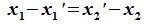
 для
для  ,
, .
.