Как найти пересечение точек на координатной прямой

План урока:

Уравнение линии в координатах

Уравнение окружности

Уравнение прямой

Задачи на пересечение двух фигур

Уравнение линии в координатах

Если какое-то уравнение содержит две переменные – х и у, то какие-то пары значений этих чисел будут являться его решением, а какие-то нет. Однако каждой такой паре чисел можно сопоставить точку на координатной плоскости. Все вместе такие точки могут образовать линию, которую можно обозначить буквой L. В таком случае исходное уравнение называют уравнением линии L.

Мы уже рассматривали некоторые уравнения линий на плоскости, когда изучали графики функций. Если некоторую функцию у = у(х) рассматривать как уравнение, то тогда график функции у(х) будет той самой линией, которая задается уравнением. Например, парабола может быть задана уравнением у = х².

Однако уравнение линии не обязательно выглядит как функция. Наиболее простой задачей является определение факта, принадлежит ли та или иная точка той линии, которая задана уравнением.

Задание. Какие из точек А (2;1), В (3; 2), С (– 2; 5) и D(0; 0) принадлежат линии, заданной уравнением:

Решение. Надо просто подставить координаты точек в уравнение и посмотреть, превратится ли оно при этом в верное равенство. Сначала подставляем точку А (2; 1):

Получилось верное равенство, значит, А принадлежит заданной линии. Теперь подставляем координаты В (3; 2):

Равенство неверное, следовательно, В на заданной линии не лежит. Проверяем третью точку С (– 2; 5):

Получили, что и С не является частью линии. Проверяем последнюю точку D (0; 0):

Справедливость равенства означает, что D принадлежит линии.

Ответ: А и D.

Использование координат и уравнений линии порождает две обратные друг другу задачи:

1) по заранее заданному уравнению определить геометрический вид линии;

2) для заданной геометрической фигуры, построенной на координатной плоскости, найти уравнение линии.

Геометрия занимается в первую очередь решением второй задачи. Первая же задача рассматривается по большей части в курсе алгебры при изучении графиков функций.

Уравнение окружности

Попытаемся составить уравнение окружности, про которую нам известен ее радиус (обозначим его буквой r) и координаты центра окруж-ти(х₀; у₀). Пусть некоторая точка М с координатами (х; у) лежит на окруж-ти. Тогда, по определению окруж-ти, расстояние между С и М равно радиусу r:

Но расстояние между точками М и С может быть вычислено по формуле

Если же точка М НЕ лежит на окруж-ти, то длина отрезка МС не будет равна r, и потому координаты М не будут удовлетворять уравнению (1). Получается, что (1) как раз и является уравнением окруж-ти.

Задание. Составьте уравнение окружности, имеющей радиус 5, если ее центр находится в точке (6; 7), и проверьте, лежат на ней точки H(2; 10)и Р(3; 8).

Решение. Сначала запишем уравнение окруж-ти в общем виде

Это и есть уравнение окруж-ти. При желании можно раскрыть скобки в правой части, но делать это необязательно. Теперь будем подставлять в полученное уравнение координаты точек Н и Р:

Проверка показала, что Н находится на окруж-ти, а Р – нет.

Задание. Начертите окружность, заданную уравнением

Именно эти значения и являются параметрами окруж-ти, которые нужны нам для ее построения. Ее центр находится в точке (х₀; у₀), то есть в (1; – 2), радиус равен r, то есть 2. В итоге выглядеть она будет так:

Особый случай представляет окруж-ть, центр которой находится в начале координат, то есть в точке (0; 0). В этом случае параметры x₀ и y₀ окруж-ти равны нулю, и уравнение

Например, окруж-ть с радиусом 4, если ее центр совпадает с началом координат, описывается уравнением:

Если при подстановке координат точки в уравнение получилось неверное равенство, то возможны два случая: либо точка находится внутри окруж-ти, либо она находится вне нее. Заметим, что в уравнении окруж-ти

левая часть представляет собой квадрат расстояния между точкой (х; у) и центром окруж-ти (х₀; у₀). Если оно больше квадрата радиуса, то точка находится вне окруж-ти, а если меньше – то внутри нее.

Задание. Определите для точек M(3; 4), N(2; 3), F(4; 4), лежат ли они на окруж-ти

x² + y² = 25

внутри нее или за пределами окруж-ти.

Решение.Снова подставляем координаты точек в уравнение окруж-ти:

Это ошибочное равенство, ведь в реальности левая часть больше:

32 > 25

Это значит, что F(4; 4) лежит вне окруж-ти. Убедиться в правильности сделанных выводов можно, построив заданную окруж-ть и отметив точки M, N и F:

Рассмотрим несколько более сложных задач по данной теме.

Задание.Запишите уравнение окружности с центром С(– 4; 2), и окруж-ть проходит через точку А(0; 5).

Решение. В данном случае радиус окруж-ти явно не указан, и его надо найти. Подставим в уравнение окруж-ти известные нам данные:

Задание. Даны точки К (– 2; 6) и М (2; 0). Запишите уравнение окруж-ти, в которой КМ будет являться диаметром.

Решение. Для составления уравнения нужно знать радиус окруж-ти и координаты ее центра. Обозначим центр буквой С. Ясно, что центр окруж-ти делит любой ее диаметр пополам, на два одинаковых радиуса, то есть является серединой диаметра. То есть С – середина КМ, а потому для поиска координат С используем формулы:

Итак, координаты центра теперь известны, это (0; 3). Чтобы найти радиус, поступим также, как и в предыдущей задаче – подставим координаты точек С и, например, К, в уравнение окруж-ти

Обратите внимание, что нам необязательно вычислять радиус, ведь для уравнении окруж-ти нужна его величина, возведенная в квадрат, и мы ее нашли. Теперь можем записать уравнение окончательно

Задание. Дано уравнение окружности

(x — 2)² + (y — 4)² = 9

Найдите точки этой окруж-ти, абсцисса которых равна 2.

Решение. Напомним, что абсцисса – это координат х точки. Она нам уже известна, х = 2. Остается только найти ординату, то есть координату у. Для этого подставим известное нам значение абсциссы в уравнение и решим его:

Обратите внимание, что у квадратного уравнения нашлось сразу 2 корня, они соответствуют двум точкам, (2; 1) и (2; 7).

Ответ: (2; 1) и (2; 7).

Задание. Составьте уравнение окружности, проходящей через точки D(3; 8), L(6; 7) и K(7; 0).

Решение. Эта задача сложнее предыдущих и потребует громоздких вычислений. Нам надо найти радиус окруж-ти r и ее центр (х₀; у₀). Запишем для точки D(3; уравнение окруж-ти:

Далее раскроем скобки в левой части, используя формулу квадрата разности (это необходимо для упрощения дальнейших расчетов):

В итоге нам удалось составить три уравнения, которые содержат три переменные: r, х₀ и у₀.Вместе они образуют систему уравнений, которую можно попробовать решить:

Далее можно, например, вычесть из (2) уравнение (3):

Нам удалось найти одно из интересующих нас чисел, у₀. С помощью (5) легко найдем и х₀:

x₀ = 7y₀ — 18 = 7*3 — 18 = 21 — 18 = 3

Итак, центр окруж-ти находится в точке (3; 3). Осталось найти радиус окруж-ти. Для этого подставим в уравнение окруж-ти вычисленные нами координаты центра, а также координаты одной из точек из условия, например, K(7; 0):

Радиус окруж-ти равен 5. Теперь мы можем окончательно записать уравнение окруж-ти

Чтобы убедиться в правильности найденного решения, можно подставить в полученное уравнение координаты трех точек из условия и посмотреть, обращают ли они его в верное равенство. Вместо этого мы для наглядности просто построим в координатной плоскости получившуюся окруж-ть и отметим на ней точки из условия:

Ответ: (х – 3)² + (у – 3)² = 25

Уравнение прямой

Пусть на координатной плоскости построена произвольная прямая m. Для составления его уравнения отметим две точки А(х₁; у₁) и В(х₂; у₂) так, чтобы прямая m оказалась серединным перпендикуляром для отрезка АВ:

Тогда, согласно свойству серединного перпендикуляра,про любую точку М(х; у), лежащую на m, можно сказать, что она равноудалена от А и В, и наоборот, любая точка, НЕ лежащая на m, НЕ равноудалена от А и В. Это означает, что для точки M, если она лежит на m, должно выполняться равенство:

Квадратные корни равны, если одинаковы их подкоренные выражения, поэтому

Заметим, что так как точки А и В – различные, то хотя бы одна из разностей (2х₂ – 2х₁) и (2у₂ – 2у₁) будет не равна нулю, поэтому в (2) хотя бы один их коэффициентов а и b точно ненулевой. Это означает, что уравнение (2) является уравнением первой степени. Заметим, что (2) называют общим уравнением прямой, так как оно описывает любую прямую на плоскости. При более глубоком изучении геометрии вы познакомитесь с множеством других видов уравнений прямой (нормальным, каноническим, тангенциальным, параметрическим и т. п.).

В последнем примере коэффициент с равен нулю, поэтому его просто не записали.

Заметим важный аспект – одна и та же прямая может описываться различными уравнениями вида (2). Например, пусть уравнение прямой выглядит так:

Это уравнение равносильно предыдущему, хотя у них и различны коэффициенты а, b и c. Это значит, что однозначно определить эти коэффициенты при решении задач в большинстве случаев невозможно. Поэтому удобней рассмотреть два отдельных случая.

1) Если коэффициент b в уравнении прямой (2) не равен нулю, то его можно привести к виду:

получим линейную функцию:

y = kx + d (3)

Из курса алгебры мы помним, что ее графиком как раз является прямая. В большинстве случаев уравнение прямой удобно записывать именно в таком виде. Напомним, что число k называется угловым коэффициентом прямой.Поэтому (3) так и называют – уравнением прямой с угловым коэффициентом. В качестве примера подобных уравнений можно привести:

Каждое из них описывает вертикальную прямую, параллельную оси Оу.

Задание. Прямая задана уравнением

4x + 2y + 6 = 0

Постройте ее на координатной плоскости

Решение. Для построения прямой надо всего лишь найти две различные точки, лежащие на ней, и соединить их. Мы будем брать произвольные значения координаты х, подставлять их в уравнение и находить соответствующее им значение координаты у. Подставим х = 1:

Получили другую точку (– 1; – 1). Осталось отметить эти две точки на и соединить их:

Задание. Составьте уравнение прямой, проходящей через точки D(1; 10) и Е(– 1; – 4).

Решение. Задачу можно решить разными способами.

Способ 1 – универсальный и более сложный.

В общем виде уравнение прямой выглядит так:

ax + by + c = 0

Нам надо найти коэффициенты а, b и c. Для этого просто подставляем координаты известных точек в уравнение. Начнем с координат D:

Нам удалось выразить коэффициента двумя различными выражениями (1) и (2). Так как в них одинаковы левые части, то можно приравнять и правые части:

Мы можем взять любое значение коэффициента с (кроме нуля), и при этом получатся различные, но равносильные друг другу уравнения. Удобно взять с = 3, тогда в уравнении исчезнут дроби:

Это и есть ответ задания.

Далее рассмотрим более простой способ, который, однако, может потребовать анализа различных вариантов.

Способ 2

Уравнение прямой может иметь либо вид

y = kx + d

если прямая является графиком линейной функции, либо вид

x = C

если прямая параллельна оси Оу. Во втором случае у всех точек прямой абсцисса должна быть одинакова, однако у точек D(1; 10) и Е(– 1; – 4) она различна, поэтому ее точно можно описать уравнением

y = kx + d

Надо найти коэффициенты k и d. Подставим в уравнение координаты D(1; 10):

Итак, уравнение можно записать так:

Задание. Запишите уравнение прямой, если ей принадлежат точки:

Подставим сюда уже известное нам значение d:

В (1) и (2) мы выразили d с помощью разных выражений, которые теперь можно приравнять:

То, что коэффициент k оказался нулевым, означает, что прямая параллельна оси Ох.

в) Попытаемся сделать те же действия, что и в двух предыдущих примерах, подставляя точки в уравнение у = kx + d:

На этот раз мы не смогли найти коэффициент k, а вместо этого получили ошибочное равенство. То есть уравнение просто не имеет решений. Что же это значит? Из этого факта следует, что в этом примере уравнение прямой НЕ может иметь вид

y = kx + b

Значит, оно имеет другой вид:

x = C

Действительно, у обеих точек (2; 7) и (2; одинаковы абсциссы. Это значит, что прямая, проходящая через них, вертикальная. Коэффициент С как раз равен значению этой абсциссы, так что уравнение выглядит так:

x = 2

Ответ а) у = 1,5х + 3; б) у = 8; в) х = 2.

Задание. Найдите площадь треугольника MON, изображенного на рисунке, если известно, что M и N лежат на прямой, задаваемой уравнением:

Решение. ∆MON – прямоугольный, и для вычисления его площади нужно найти длины OM и ON. По рисунку видно, что М лежит на оси Ох, то есть у неё ордината нулевая:

y_M = 0

Зная это, легко найдем и абсциссу М, ведь координаты М при их подстановке в уравнение прямой должны давать верное равенство:

Далее рассмотрим точку N. Она уже лежит на Оу, а потому у нее нулевой оказывается абсцисса:

Напомним, что площадь прямоугольного треугольника может быть вычислена по формуле:

Задачи на пересечение двух фигур

Метод координат помогает находить точки, в которых пересекаются те или иные геометрические фигуры. В большинстве случаев надо просто составить систему из уравнений, задающих эти фигуры, и найти их общее решение. В курсе алгебры мы уже рассматривали как решение простых, в основном линейных систем, так и решение более сложных, нелинейных систем. Рассмотрим несколько задач на эту тему.

Задание. Две прямые заданы уравнениями:

Определите, в какой точке они пересекаются.

Решение. Если точка пересечения прямых существует, то ее координаты являются решением каждого из двух уравнений. Таким, образом, нам надо просто решить систему:

Мы нашли единственное решение системы – это пара чисел (3; – 2). Эта же пара определяет координаты искомой нами точки.

Ответ: (3; – 2).

Задание. Найдите точки пересечения окруж-ти и прямой, если они задаются уравнениями

Решаем квадратное уравнение, используя дискриминант:

Мы нашли два различных значения у. Это значит, что прямая пересекается с окруж-тью в двух различных точках, а найденные нами числа – их ординаты. Отметим, что возможны случаи, когда корень только один (и тогда у окруж-ти с прямой одна общая точка, то есть они касаются), и когда корней вовсе нет (тогда окруж-ть и прямая не пересекаются). В нашем же примере осталось найти абсциссы точек. Для этого используем уравнение (3):

Получили в итоге пары точек (3; и (6; 7), в которых заданная окруж-ть и прямая пересекаются.

Ответ: (3; и (6; 7).

Задание. Две окруж-ти заданы уравнениями:

Для ее решения сначала раскроем скобки в обоих уравнениях и приведем подобные слагаемые:

Нам удалось выразить у через х. Теперь снова запишем одно из исходных уравнений окруж-ти, но заменим в нем у с помощью только что найденного выражения:

Мы нашли абсциссы точек пересечения окруж-тей, теперь можно вернуться к (1), чтобы найти и ординаты:

Получили точки (5; 2) и (4; 3).

Ответ:(5; 2) и (4; 3).

В конце решим одну задачу чуть более высокого уровня сложности.

Задание. К окруж-ти радиусом 5, чей центр совпадает с началом координат, построена касательная в точке (3; 4). Составьте уравнение этой касательной.

Решение. Сначала составим уравнение окруж-ти. Так как ее центр находится в начале координат, а радиус имеет длину 5, то оно примет вид:

Нам надо найти коэффициенты k и d, а для этого надо составить какие-нибудь уравнения с этими переменными. Нам известно, что касательная проходит через точку (3; 4), а потому эти координаты можно подставить в (2):

Обратите внимание, что мы получили квадратное уравнение относительно переменной х. Если бы нам были известны k и d, то мы смогли бы его решить, и тогда мы определили бы точки пересечения прямой и окруж-ти. В этой задаче k и d нам неизвестны, но мы знаем, что окруж-ть и прямая касаются, то есть имеют ровно одну общую точку. Но тогда и квадратное уравнение (4) должно иметь только одно решение! Это означает, что его дискриминант равен нулю. Сначала выпишем коэффициенты квадратного уравнения, используемые при вычислении дискриминанта:

Теперь у нас есть два уравнения, (3) и (5), которые содержат только переменные k и d. Осталось лишь совместно решить их. Для этого подставим (3) в (5):

В рамках урока мы выяснили, как выглядят уравнения окруж-ти и прямой, а также научились решать несколько типовых заданий, в которых эти уравнения необходимо использовать. Хотя формулы, используемые при этом, могут показаться слишком сложными, главное – просто набить руку в их применении, решая как можно больше задач.

Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x₁-x₂) никак не разделить и т.д.

Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.

Коэффициенты А, B, C

Все помним со школы формулу:

Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):

Те же фаберже, только сбоку.

В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.

Загвоздка в том, что мы не знаем коэффициенты для обеих линий.

В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:

Путем несложных операций приходим к следующей записи:

Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:

Пока все идет отлично, нигде вероятного деления на ноль не встретилось.

Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.

Система уравнений

Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.

Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.

Сразу же запишем метод под нашу систему.

Имеем следующую систему:

Определители будут такими:

Исходя из метода, решение выглядит так:

Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности).  В коде, естественно, этот момент надо учитывать.

Практика 1

Частные случаи

• Прямые параллельны: ∆_ab = 0
  • (A₁B₂ – B₁A₂ = 0);
• Прямые совпадают:  ∆_ab = ∆_X = ∆_Y = 0 
  • (A₁B₂ – B₁A₂ = 0) И (A₁C₂ — A₂C₁ = 0) И (C₁B₂ -B₁C₂ = 0);
• Прямые перпендикулярны:
  • (A₁ A₂ + B₁ B₂ = 0).

Принадлежность точки отрезку

В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:

1. Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
2. Проверить факт нахождения точки между концами отрезка.

Займемся пунктом 2. Данный факт можно установить двумя способами:

• Логически, т.е. (x₁ <= x <= x₂) ИЛИ (x₁ >= x >= x₂). На случай «вертикальности» линии добавить проверку на Y:
  • (y₁ <= y <= y₂) ИЛИ (y₁ >= y >= y₂).
• Арифметически. Сумма отрезков |x-x₁| + |x-x₂| должна быть равна длине отрезка |x₁-x₂|. Аналогично, на случай «вертикальности» , добавить проверку:
  • |y-y₁| + |y-y₂| = |y₁-y₂|

Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.

Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.

Угол пересечения прямых

Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p₁ и p₂, получим направляющий вектор V(p₁,p₂), и аналогично второй вектор M(p₃,p₄). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.

Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:

α — угол наклона вектора к оси X, который можно найти, как:

α = arctan (A₁ / B₁)

Где расстояния:

A₁ = (y₁ — y₂)

B₁ = (x₂ — x₁)

Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…

Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.

Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.

По рисунку явно видно, что угол между векторам это γ = (β — α).

В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.

От теории к практике

Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.

Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.

Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:

Тут ситуация с вертикальной прямой, т.е. когда теоретически происходит деление на ноль, явно не обрабатывается. Она корректно обрабатывается функцией ArcTan2, которая вернет в этом случае и знак, и 90 градусов.  

Практика 2

В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.

Исходники

Небольшие комментарии по интерфейсу.

Скачать (219 Кб): Исходники (Delphi XE 7-10)

Скачать (1.14 Мб): Исполняемый файл

При запуске генерируется случайным образом 4 точки, по две на прямую. Точки и отрезки можно перетаскивать мышкой. Также, слева присутствует панель, на которой можно ввести координаты точек или коэффициенты уравнения прямой. При нажатии «Enter» или когда элемент ввода теряет фокус, происходит перерасчет и перерисовка.

Внизу есть 4 кнопки переключения режимов отображения. Начиная со второй, помимо координат точки пересечений в верхнем левом углу будет отображаться текущий угол пересечения между направляющими векторами.

Если точка пересечений попадает в какой-либо из отрезков, соответствующий заголовок линии отрезка станет жирным. На рисунке это зеленая линия 2.

По умолчанию, рабочее поле системы координат имеет размерность [-10..10], которую можно изменить ползунком в нижнем правом углу.

Точка пересечения двух прямых на плоскости

Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.

Точка пересечения двух прямых в пространстве

Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.

В данной публикации мы рассмотрим, что такое точка пересечения двух прямых, и как найти ее координаты разными способами. Также разберем пример решения задачи по этой теме.

• Нахождение координат точки пересечения

• Пример задачи

Нахождение координат точки пересечения

Пересекающимися называются прямые, которые имеют одну общую точку.

M – точка пересечения прямых. Она принадлежит им обоим, значит ее координаты одновременно должны удовлетворять обоим их уравнениях.

Для нахождения координат этой точки на плоскости можно использовать два способа:

• графический – чертим графики прямых на координатой плоскости и находим их точку пересечения (не всегда применимо);
• аналитический – более универсальный метод. Мы объединяем уравнения прямых в систему. Затем решаем ее и получаем требуемые координаты. От количества решений зависит то, каким образом ведут себя прямые по отношению друг к другу:
  • одно решение – пересекаются;
  • множество решений – совпадают;
  • нет решений – параллельны, т.е. не пересекаются.

Пример задачи

Найдем координаты точки пересечения прямых y = x + 6 и y = 2x – 8.

Решение

Составим систему уравнений и решим ее:

В первом уравнении выразим x через y:
x = y – 6

Теперь подставим полученное выражение во второе уравнение вместо x:
y = 2 (y – 6) – 8
y = 2y – 12 – 8
y – 2y = -12 – 8
-y = -20
y = 20

Значит, x = 20 – 6 = 14

Таким образом, общая точка пересечения заданных прямых имеет координаты (14, 20).

Как вычислить точки пересечения прямых

Две прямые, если они непараллельны и не совпадают, обязательно пересекаются в одной точке. Найти координаты этого места – значит вычислить точки пересечения прямых. Две пересекающиеся прямые всегда лежат в одной плоскости, поэтому достаточно рассмотреть их в декартовой плоскости. Разберем на примере, как найти общую точку прямых.

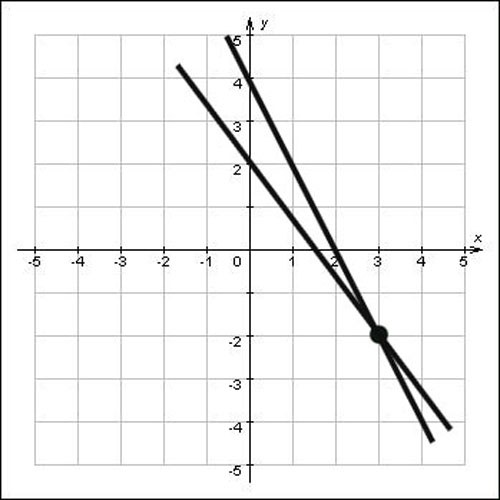
Инструкция

Возьмите уравнения двух прямых, помня о том, что уравнение прямой в декартовой системе координат уравнение прямой выглядит как ах+ву+с=0, причем а, в, с – обычные числа, а х и у – координаты точек. Для примера найдите точки пересечения прямых 4х+3у-6=0 и 2х+у-4=0. Для этого найдите решение системы этих двух уравнений.

Для решения системы уравнений измените каждое из уравнений так, чтобы перед y стоял одинаковый коэффициент. Так как в одном уравнении коэффициент перед у равен 1, то просто умножьте это уравнение на число 3 (коэффициент перед у в другом уравнении). Для этого каждый элемент уравнения умножьте на 3: (2х*3)+(у*3)-(4*3)=(0*3) и получите обычное уравнение 6х+3у-12=0. Если бы коэффициенты перед у были отличны от единицы в обоих уравнениях, умножать надо было бы оба равенства.

Вычтите из одного уравнения другое. Для этого вычтите из левой части одного левую часть другого и точно также поступите с правой. Получите такое выражение: (4х+3у-6) — (6х+3у-12)=0-0. Так как перед скобкой стоит знак «-», все знаки в скобках поменяйте на противоположные. Получите такое выражение: 4х+3у-6 — 6х-3у+12=0. Упростите выражение и вы увидите, что переменная у исчезла. Новое уравнение выглядит так: -2х+6=0. Перенесите число 6 в другую часть уравнения, и из получившегося равенства -2х=-6 выразите х: х=(-6)/(-2). Таким образом, вы получили х=3.

Подставьте значение х=3 в любое уравнение, например, во второе и получите такое выражение: (2*3)+у-4=0. Упростите и выразите у: у=4-6=-2.

Запишите полученные значения х и у в виде координат точки (3;-2). Эти и будет решение задачи. Проверьте полученное значение методом подстановки в оба уравнения.

Если прямые не даны в виде уравнений, а даны просто на плоскости, найдите координаты точки пересечения графически. Для этого продлите прямые так, чтобы они пересеклись, затем опустите на оси ох и оу перпендикуляры. Пересечение перпендикуляров с осями ох и оу, будет координатами этой точки, посмотрите на рисунок и вы увидите, что координаты точки пересечения х=3 и у=-2, то есть точка (3;-2) и есть решение задачи.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?