Как найти периметр балкона

Как найти периметр и площадь в начальной школе

Площадь и периметр – значения, вычисление которых формирует пространственное мышление у детей, а это представляет сложность в начальной школе.

Но освоение величин необходимо для приобретения практических навыков в жизни и дальнейшего изучения основ математики.

В разных учебных программах начальной школы эти темы изучают со 2-4 класса. Например, в учебнике математики Рудницкой, тема «Периметр и площадь» изучается во 2 классе.

Почему ученики начальной школы путают понятия «площадь» и периметр» и как помочь ребенку разобраться в теме, рассмотрим подробнее.

Отличие площади от периметра

Отличать понятие «площадь» от «периметра» школьнику начальных классов трудно, потому что это абстракция, а формулы-математические символы, вообще, трудно понять и представить. Поэтому на первых этапах формулы пугают учеников начальной школы, а задачи на нахождение периметра и площади остаются за гранью восприятия. Путаница заключается еще и в том, что учащиеся не видят разницы между линейными и квадратными единицами измерения.

В начальной школе находят площадь и периметр таких фигур как квадрат, прямоугольник и треугольник.

Что такое площадь и периметр?

Площадь определяет размер места, занимаемого фигурой на плоскости или поверхности

Еще можно сказать, что площадь — это пространство, которым полностью заполнена плоская фигура внутри. Измеряют площадь в квадратных единицах длины: квадратных сантиметрах, метрах, миллиметрах, дюймах и т.д.

Площадь обозначают латинской буквой S.

Площадь и периметр

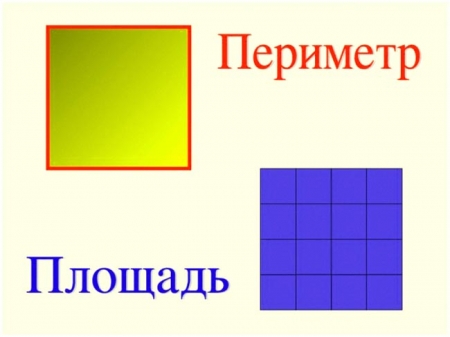
Периметр – величина, обозначающая длину контура фигуры или забор вокруг огорода. Если обвести фигуру по контуру, длина получившейся линии будет означать периметр

Измеряют периметр в единицах длины: сантиметры, метры, километры, дюймы и т.д. Периметр обозначают латинской буквой Р.

Оба понятия характеризуют размер фигуры и определяются значением ее сторон, возникает путаница в голове у ученика начальной школы.

5 практических способов усвоения понятий «площадь» и «периметр»

Чтобы научиться быстро отличать площадь от периметра, важно использовать наглядность – предметы-модели и отрабатывать навыки расчета на практике.

1. Игровой метод

При построении на плоскости с помощью конструктора Lego, кубиков или мозаики «полных» и «пустых» фигур можно наглядно объяснить ребенку разницу между двумя величинами.

Игровой способ запоминания понятий площадь и периметр

2. Графический способ

Карандашами, фломастерами или красками рисуют на бумаге фигуры или предметы. С помощью объекта, нарисованного одной линией, представляют периметр. Закрашивая фигуру внутри, показывают площадь. Деление прямоугольника на квадраты по длине и ширине – это площадь

Графический способ

3. Ассоциативный метод

Ограждение выступает периметром, а пространство внутри него площадью. Рассмотреть наглядно можно поверхность предметов в квартире: стол, табурет, коврик, двери и прочие предметы.

Площадь пола в квартире

Например: рама в окне – периметр, а вставленное стекло – площадь. Картошка в огороде или линолеум в кухне – это площадь прямоугольника. Ограждение вокруг участка, бордюр вокруг стоянки – периметр.

Периметр забора

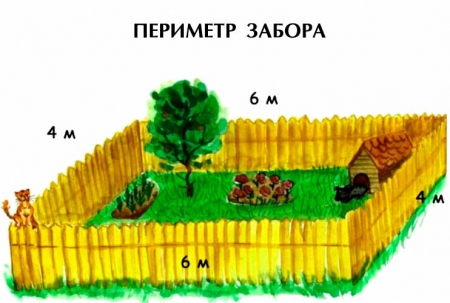
4. Построение каркаса

Сделайте каркас квадрата из ниток, спичек, веревки или проволоки – это и есть периметр.

Каркас из спичек

5. Метод трафаретов

Для наглядного представления площади и периметра из бумаги или тонкого картона вырезают два трафарета одной фигуры. Один используют для штриховки (площадь), другой для обводки (периметр). Сравнение и наложение их друг на друга.

Трафареты в линейке

Когда ученик научился различать эти две величины, можно переходить к формулам и решению задач.

Как найти площадь прямоугольника и квадрата по формуле

Формула нахождения площади прямоугольника: S = ab, где а – длина, b – ширина прямоугольника.
Площадь квадрата находят по формуле: S = aa, где а – длина и a – ширина квадрата.

Формулы нахождения площади

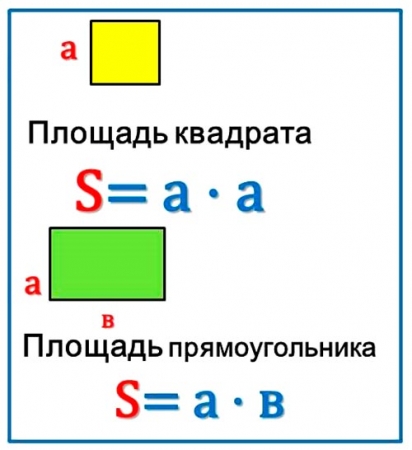
Квадрат – это прямоугольник, у которого все углы прямые, а стороны равны. Равные стороны обозначают одинаковой буквой «а».

Рассмотрим, как найти периметр прямоугольника и квадрата по формуле.

В школьных учебниках начальной школы дается определение нахождения периметра: «Периметр — это сумма длин всех сторон фигуры», следовательно, чтобы его найти нужно сложить длины всех сторон.

Формула нахождения периметра прямоугольника: P = а + а + b + b или P=(а+b)*2 или так P = 2ab + 2ab, где буквами а, b обозначена длина и ширина сторон прямоугольника.

Формулы нахождения периметра прямоугольника и квадрата

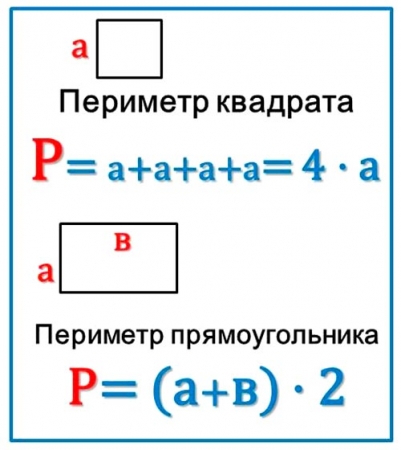
У прямоугольника длина и ширина разные, они обозначаются «а» и «b». Противоположные стороны равны в прямоугольнике, следовательно, в формуле они встречаются 2 раза или сумма длины и ширины умножается на 2.

Периметр квадрата находят по формуле: P = а + а + а + а или P=4*а, где а – длина каждой стороны с одинаковой длиной.

Примеры задач на нахождение периметра и площади

Задача № 1

Маленькому щенку купили коврик прямоугольной формы. Сколько места займет коврик в прихожей, если его длина 4 дм, а ширина 3 дм?

Решение:
Для того чтобы определить, сколько места займет коврик, нужно рассчитать его площадь (размер поверхности). Для этого умножаем ширину на длину: 3 x 4 = 12 дм²

Ответ: площадь коврика составляет 12 дм² (1200 см²).

Задача № 2

Площадь квадратного балкона в бабушкиной квартире равна 9 м². Определите периметр балкона.

Решение:
У квадрата все стороны равны. Площадь определяется умножением длины на ширину. Число 9 можно представить в виде произведения двух одинаковых чисел.

1. 9 : 3 = 3 м (ширина и длина)
2. 3 + 3 + 3 + 3 = 3 x 4 = 12 м (периметр)

Ответ: периметр балкона составляет 12 м.

Задача № 3

Для украшения детской площадки к Новому году было решено купить гирлянду из лампочек и укрепить ее на ограждении. Длина прямоугольной детской площадки 5 м, ширина 6 м. Найдите периметр для определения нужной длины гирлянды.

• Первый способ: 5 + 5 + 6 + 6 = 22 м
• Второй способ: 2 x 5 + 2 x 6 = 22 м
• Третий способ: 2 x (5 + 6) = 22 м

Ответ: периметр детской площадки и длина гирлянды составляет 22 м.

Пишите в комментариях, какие способы разведения понятий «площадь» и «периметр» помогли Вам или вашему ребенку.

— совершенствовать умения составлять выражения для вычисления периметра прямоугольника и квадрата разными способами.

развитие восприятия, наблюдательности внимания, пространственных представлений, умения выделять главный признак, классифицировать обобщать, развитие логики, навыков вычисления периметра многоугольника, развитие математической речи, критического и практического мышления.

воспитание интереса к математике, познанию, творчеству, воспитание самостоятельности, организованности, трудолюбия, аккуратности, чувства дружбы и товарищества.

развитие познавательных интересов, учебных мотивов.

Регулятивные: принимать и сохранять учебную задачу и планировать своё действие в соответствии с поставленной задачей и условиями её реализации.

формировать умение находить периметр многоугольника.

Коммуникативные: умение работать в парах, контролировать действия партнера.

Тип урока : урок усвоения новых знаний.

Методы урока: объяснительный, иллюстративный, проблемный.

— компьютер, мультимедийный проектор, экран;

— учебник «Математика. 4 класс»/ М.И. Башмаков, Н.Г. Нефедова. -М.:Астрель,2014г.

раздаточный материал для учащихся, карточки для самостоятельной работы;

задания для выполнения на уроке;

Формы организации учебной деятельности:

фронтальная групповая индивидуальная

I. Организационный момент:

– С хорошим настроением начинаем наш урок. Посмотрите друг другу в глаза, улыбнитесь, мысленно пожелайте друг другу добра, удачи, успехов.

— Руки? — На месте!
— Ноги? — На месте!
— Локти? — У края!
— Спинка? – Прямая!

– Кто из вас любит путешествовать? Поднимите руку.
– А для чего люди путешествуют? (Чтобы узнать что-то новое.)

Прозвенел уже звонок,

В путешествие пойдем,

В страну сказок попадем.

Слушай, думай, наблюдай,

Сказку радостно встречай!

– Но прежде чем открыть что– то новое , что нужно сделать? (Повторить старое.)

-Начинаем нашу работу с устного счета, который и поможет определить, в какую страну мы попадем.

— Расположите величины в порядке их возрастания

Находят табличку с полученным ответом, на обратной стороне написана буква. Составляют слово

— Умнички, мы с Вами действительно попали сегодня в удивительную Страну Чудес! А гости нашего урока — девочка Алиса и её друзья.

— Давайте откроем тетради и запишем число, классная работа.

III Актуализация имеющихся знаний:

— Какая геометрическая фигура лишняя и почему? ( 1 фигура – лишняя ,незамкнутая ломаная, остальные – замкнутые ломаные, многоугольники)

-У каждого из вас на парте лежит геометрическая фигура. ( Квадрат, четырехугольник, прямоугольник, многоугольник).

-Как она называется? Как вы это определили? (квадрат, четырехугольник, прямоугольник, многоугольник).

Создание проблемной ситуации

Перед вами не простые фигуры, а основа для открытки. Скоро праздник и Алиса решила сделать открытку для мамы и хочет украсить её лентой. Но у неё возникла проблема, и она попросила вас помочь ее решить. Она не знает, хватит ли ей ленты. Сможем ли мы помочь в решении этой проблемы?

— Как мы поступим в такой ситуации? С чего начнем? (Измерим длину стороны)

— Что сделаем потом? (Сложим полученные результаты)

Практическая работа (Измерение длин сторон квадрата)

— Сколько сторон у нашей фигуры? (4)

— А сколько измерений нам нужно выполнить?

— Чему равны длины сторон? (ответы)

— Сможем ли теперь узнать, сколько нужно ленты?

— Что для этого сделаем? (Сложим результаты измерений)

— Какое действие мы использовали для решения задачи? (Сложение)

— Как называется результат сложения? (Сумма)

— Что мы складывали? (Длины сторон).

— Чтобы помочь Алисе, что же мы нашли? (Сумму длин сторон)

— Давайте проверим, хватит ли ленты.

— А кто знает, как называют по – другому, сумму длин сторон? Назовите.

— Правильно, в математике эта величина имеет особое название – периметр.

— Так чем же мы сегодня на уроке будем заниматься? (Ответы детей)

— Мы узнаем, как найти периметр многоугольника. Это и будет темой нашего урока.

Ребята, а кто из Вас помнит, что обозначает слово “ Периметр”?

Ребята, я Вам напомню. В Древнем Египте границы земельных участков измерялись ходьбой, т.е. египтяне шли по границе своего участка и измеряли его. Здесь и появилось слово «периметр» (на доску вывешивается табличка со словами «пире» и «метрос»).

«Пире» – означает «ходить».
«Метрос» – измерять, т.е. измерять ходьбой.

— А кто из Вас помнит, как мы обозначаем периметр? (Обозначаем буквой P).

— А зачем нам нужно знать, что такое периметр?

— Где в нашей жизни нам могут пригодиться эти знания? (Классная доска, платье сшить, парту измерить можно.)

— Молодцы! Давайте отдохнем!

Гимнастика для глаз

ІV Актуализация новых знаний.

Слайд 7

— Алиса нашла сундук с кладом, но он закрыт на замок. Давайте вместе подберем ключ. Но без секретного кода нам сундук не открыть. Необходимо посчитать периметр фигур.

— Рассмотрите данные фигуры (учащиеся открывают с. 58 учебника №1).

— Как их можно назвать одним словом? (многоугольники)

— Что необходимо знать для вычисления периметра многоугольника? ( длину каждой из сторон)

— Что заметили? (По условию стороны равные, значит длины сторон одинаковые)

— Итак, осталось выяснить, как его вычислять. Это вам придется сделать самим в парах.

Самостоятельная работа (в парах).

1 группа вычисляет Р треугольника.
2 группа вычисляет Р четырёхугольника.
3 группа вычисляет Р пятиугольника.

4 группа вычисляет Р шестиугольника.

Делается вывод. На доске появляются записи.

Р — сумма длин 3-х сторон

Р — сумма длин 4-х сторон

Р — сумма длин 5-ти сторон и т.д.

— Какой великолепный клад мы нашли! Что мы сейчас делали? (учились вычислять периметр многоугольника)

Слайд 8

— Ребята, а вот и Чеширский кот, он предлагает нам составить выражения для вычисления периметра прямоугольника и квадрата разными способами. Проверьте друг друга. ( №2 с.58 Работа в парах)

— Как же правильно выполнить записи?

Р = 8 дм + 8 дм + 8 дм + 8 дм = 32 дм — 1 ученик выходит к доске

— А можно ли вычислить более удобным способом? (8дм*4, так как все стороны квадрата равны)

Р = 7 дм + 9 дм + 7 дм + 9 дм =32 дм

— Как можно вычислить более удобным способом?

Р = 7 дм*2 + 9 дм *2 =32 дм или Р = ( 7 дм + 9 дм) *2 =32 дм

-Как пришли к такому выводу? (Противоположные стороны прямоугольника равны)

— Обозначим длины сторон квадрата и прямоугольника буквами. Задание: Подумайте, какие выражения подходят для вычисления периметра квадрата, а какие для вычисления периметра прямоугольника. (Работа в парах. Взаимопроверка.)

— Почему выбрали именно эти формулы? (Представители каждой группы доказывают правильность своего решения.)

-Давайте проверим, внимание на Слайд 9.

— Молодцы, мы хорошо поработали, давайте поапплодируем себе.

Физминутка (упражнения на расслабление мышц опорно – двигательного аппарата)

V Закрепление нового материала.

— Итак, продолжите мою мысль: чтобы найти периметр многоугольника, нужно точно знать . (сколько сторон у многоугольника, их длину и правило нахождения периметра).

Слайд 10

— Ой, а кто это? Да это же Труляля и Траляля, а что они тут делают?

— Дело в том, что уважаемые наши гости решили задачу, но кто из них решил правильно, определить не могут. Ребята, давайте поможем им.

1. Решение задачи № 4 (а) с.58 ( один ученик у доски)

— Можем ли сразу ответить на вопрос задачи? (нет)

— Почему? ( Неизвестна длина одной из сторон прямоугольника)

— Можем ли её найти? Каким действием? (Можем, сложением). Решение.

— Зная длину и ширину прямоугольника, можем ли мы найти периметр? (Да)

— Что для этого нужно знать? (правило нахождения периметра прямоугольника). Решение. Ответ.

2. Решение №5 с.59

— Ребята, Алиса со своими друзьями очень любит спорт, особенно прыгать и бегать. Давайте вместе с ними решим задачу № 5 с.59.
На плане изображён стадион, размеры которого указаны в условии задачи. Вокруг стадиона проложена беговая дорожка.

— Что нужно найти? ( Нужно найти её длину, а ответ выразить в более крупных единицах)

— Как по-другому сформулировать вопрос задачи? (Найти периметр)

— В каких единицах измерения можно вычислить Р? (м, км)

Один решает у доски с комментированием.

( 600 м -345 м=255 м – длина, (600 м +255 м)*2= 1710 м =1 км 710 м)

VI Повторение пройденного материала

Самостоятельная работа с последующей проверкой.

— Ребята и снова Алисе понадобилась наша помощь, дело в том, что рост Алисы 1м20 см. В Стране Чудес её рост постоянно менялся. Алиса выпила напиток, напоминающий вишнёвый пирог, ананас, жареную индейку и сливочную помадку, и стала в 6 раз меньше. Затем Алиса съела пирожок, и её рост увеличился в 24 раза. Нужно узнать, на сколько больше своего нормального роста стала Алиса?

(Один человек решает у доски, за шторкой. Есть дети, которые справятся с этим заданием быстрее остальных, им дополнительно решить задания №6)

VII. Подведение итогов (Слайд 11)

— Молодцы, мы подошли к финалу нашего урока.

— Наше путешествие закончилось.

— Пора оценить свою работу на уроке.

— Что мы делали сегодня на уроке?

-Что нового узнали?

— Что называют периметром многоугольника?
— Как найти периметр треугольника? прямоугольника? квадрата? многоугольника?

— Где применяется знание о периметре в жизни?

VII Домашнее задание.

— Измерить в своей квартире периметр входной двери в дециметрах.

— Начертите в тетради фигуры, имеющие одинаковый периметр, но разную форму.

VII I Рефлексия.

— Отметьте мнение о своей работе на уроке:

Зеленый цвет — «На уроке мне всё было понятно. Я со всеми заданиями справился самостоятельно».

Желтый цвет – «На уроке мне почти всё было понятно. Не всё получалось сразу, но я всё равно справился с заданиями».

ПЕРИМЕТР это

ПЕРИМЕТР, -а, м. В математике: граница плоской фигуры, а также длина этой границы. II прил. периметрический, -ая, -ое.

Морфология

• Существительное, неодушевленное, мужской род

Книги

… задачи на движение, задачи на дроби и проценты, задачи на нахождение площади и периметра прямоугольника и квадрата, задачи на производительность труда и нахождение стоимости. В книге в доступной форм…

…том. Они разные по возрасту: самой старшей уже более 250 лет, а самой молодой – всего около 50, и по размеру: периметр самой маленькой – 280 метров, а самой большой – 690 метров, но все удивительно ин…

Тренинговая тетрадь предназначена для отработки предметных навыков по основным темам программы начальной школы. Она предполагает как самостоятельную работу учащихся в школе и дома, так и выполнение заданий под руководством учителя или родителей. Тетрадь состоит из набора карточек со сквозной нумерацией, листов фиксации достижений школьников и ответов для проверки. Тетрадь можно использовать при закреплении изучаемой темы и на этапе повторения, для подготовки к контрольным работам и выявления пробелов в знаниях.

…более значительных божеств. Эти более важные персонажи, выставленные вдоль стенок по всему периметру витрины, всем своим видом, казалось, назначены были являть собственное подавляющее превосходство. Н…

…ливый ученый, международный террорист и ставленник преступных корпораций. С какой целью Радич проникает за периметр одного из Барьеров, неизвестно, но ясно одно – ничего хорошего человечеству он оттуд…

Что такое периметр? Как найти периметр?

Геометрия, если не ошибаюсь, в мое время изучалась с пятого класса и периметр был и есть одним из ключевых понятий. Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P). Вообще, трактуют данный термин по разному, например,

• общая длина границы фигуры,
• длина всех ее сторон,
• сумма длин ее граней,
• длина ограничивающей фигуру линии,
• сумма всех длин сторон многоугольника

И так далее, однако, сути это не меняет.

Для различных фигур существуют свои формулы определения периметра. Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:

1. для квадрата,
2. для прямоугольника,
3. для параллелограмма,
4. для куба,
5. для параллелепипеда

Периметр квадрата

Для примера возьмем самое простое — периметр квадрата.

Все стороны квадрата равны. Пусть одна сторона носит название «a» (также, как и остальные три), тогда

или более компактная запись

Периметр прямоугольника

Усложним задачу и возьмем прямоугольник. В данном случае уже нельзя сказать, что все стороны равны, поэтому пусть длины сторон прямоугольника будут равны a и b.

Тогда формула будет иметь следующий вид:

Периметр параллелограмма

Аналогичная ситуация будет и с параллелограммом (см. периметр прямоугольника)

Периметр куба

Что же делать, если мы имеем дело с объемной фигурой? Например, возьмем куб. Куб имеет 12 сторон и все они равны. Соответственно, периметр куба можно вычислить следующим образом:

Периметр параллелепипеда

Ну, и для закрепления материала вычислим периметр параллелепипеда. Тут необходимо немного поразмышлять. Давайте делать это вместе. Как мы знаем, прямоугольный параллелепипед представляет собой фигуру, сторонами которой являются прямоугольники. У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть

(2a + 2b) * 2 = 4a + 4b

Но ведь у нас есть еще и сторона «c». Значит формула для вычисления периметра параллелепипеда будет иметь следующий вид:

Как видно из примеров выше, всё, что необходимо сделать для определения периметра фигуры — найти длину каждой из сторон, а затем их сложить.

В заключение хочется отметить, что не всякая фигура имеет периметр. К примеру, у шара периметра нет.