Как найти периметр через радиус описанной окружности

Периметр Правильного Треугольника: Определение и Формулы

Правильный треугольник — это треугольник, у которого
все стороны и углы равны.

Правильный треугольник, также называют равносторонним
и равноугольным. Все углы в таких треугольника имеют
градусную меру в 60 градусов.

Периметр правильного треугольника — это периметр
треугольника, у которого все стороны и углы равны.

Периметр в правильном треугольнике, можно найти с
помощью площади, длины сторон, радиуса и так далее.

Формула периметра
правильного треугольника

1. Формула периметра правильного треугольника, через сторону:

Формула периметра правильного треугольника, через радиусвписанной окружности:

Формула периметра правильного треугольника, через радиус описанной окружности:

Формула периметра правильного треугольника, через площадь:

С помощью этих формул можно найти периметр через площадь,
сторону, радиус вписанной и описанной окружностей.

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Найти периметр зная радиус описанной окружности

Периметр квадрата

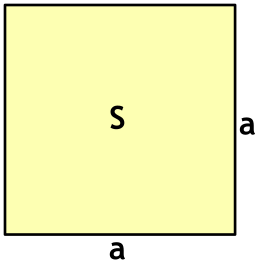
Квадрат – это геометрическая фигура, у которой все стороны равны и все углы прямые.

Выберите нужный калькулятор, введите данные и нажмите кнопку «Посчитать».

Периметр квадрата по стороне = 0
Периметр квадрата по диагонали = 0
Периметр квадрата по радиусу описанной окружности = 0
Периметр квадрата по радиусу вписанной окружности = 0

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Онлайн калькулятор периметра квадрата описанного около окружности. Как узнать периметр квадрата описанного около окружности.

Вычислить периметр квадрата описанного около окружности через:

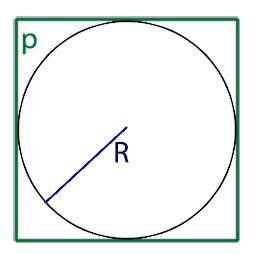
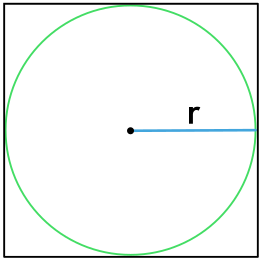
Радиус круга R:

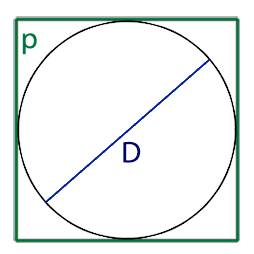
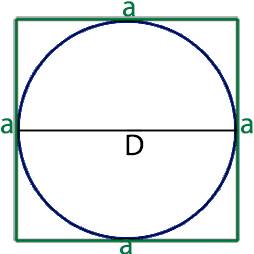
Для того, что бы узнать периметр квадрата описанного около окружности необходимо с тем что у этих двух фигур общее, а одной из общих величин у них является сторона квадрата которая равна диаметру круга.

Таким образом для нахождения периметра квадрата описанного около окружности, через этот круг, необходимо найти значение диаметра.

Для нахождения диаметра окружности нам необходимо знать одну из его величин а именно:

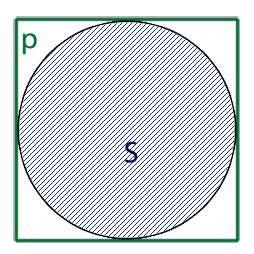
1. либо площадь круга, обозначаемая буквой S,
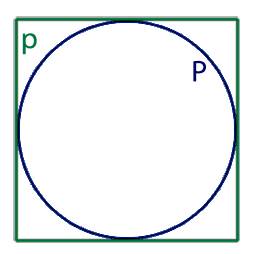
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

Соответственно если мы знаем диаметр круга который равен стороне описанного квадрата,

Теперь мы можем узнать периметр этого квадрата

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Выбирайте формулу в зависимости от известных величин.

1. Как найти периметр треугольника, зная три стороны

Просто посчитайте сумму всех сторон.

• P — искомый периметр;
• a, b, c — стороны треугольника.

2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности

Умножьте площадь треугольника на 2.

Разделите результат на радиус вписанной окружности.

• P — искомый периметр;
• S — площадь треугольника;
• r — радиус вписанной окружности.

3. Как вычислить периметр треугольника, зная две стороны и угол между ними

Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:

• Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
• Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
• Найдите корень из результата.

Теперь прибавьте к найденной стороне две ранее известные стороны.

• P — искомый периметр;
• b, c — известные стороны треугольника;
• ɑ — угол между известными сторонами;
• a — неизвестная сторона треугольника.

4. Как найти периметр равностороннего треугольника, зная одну сторону

Умножьте сторону на 3.

• P — искомый периметр;
• a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).

5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание

Умножьте боковую сторону на 2.

Прибавьте к результату основание.

• P — искомый периметр;
• a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
• b — основание треугольника (это сторона, которая отличается длиной от остальных).

6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту

Найдите квадраты боковой стороны и высоты.

Отнимите от первого числа второе.

Найдите корень из результата и умножьте его на 2.

Прибавьте к полученному числу две боковые стороны.

• P — искомый периметр;
• a — боковая сторона треугольника;
• h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).

7. Как вычислить периметр прямоугольного треугольника, зная катеты

Найдите квадраты катетов и посчитайте их сумму.

Извлеките корень из полученного числа.

Прибавьте к результату оба катета.

• P — искомый периметр;
• a, b — катеты треугольника (стороны, которые образуют прямой угол).

8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу

Посчитайте квадраты гипотенузы и катета.

Отнимите от первого числа второе.

Найдите корень из результата.

Прибавьте катет и гипотенузу.

• P — искомый периметр;
• a — любой катет прямоугольника;
• c — гипотенуза (сторона, которая лежит напротив прямого угла).

Правильный шестиугольник — это выпуклая многоугольная фигура с шестью сторонами одинаковой длины и
углами равной величины. Другое название — гексагон. Он имеет ряд следующих особенностей и
признаков:

• Длина стороны равнозначна радиусу описанной вокруг него окружности.
• Длинная диагональ представляет собой диаметр описанной окружности вокруг шестиугольника и её
  числовое значение — это удвоенная величина стороны.
• Короткая диагональ этой фигуры  больше его стороны в √3 раза.
• Величина каждого из шести углов имеет значение 120 градусов.
• Короткая диагональ гексагона — это перпендикуляр к одной из его сторон.
• Прямоугольный треугольник, который образуется посредством одной из сторон данной фигуры, а также
  его диагоналями — короткой и длинной, — имеет острые углы 30 и 60 градусов.
• Если провести 6 длинных диагоналей, то образуется 6 правильных треугольников. Все их углы будут
  по 60 градусов, а каждая высота равнозначна радиусу окружности, вписанной в данную фигуру.

Вариантов нахождения периметра гексагона существует множество. Например, с использованием диагоналей
и площади. Ведь по условию не всегда известна длина стороны.

Через площадь

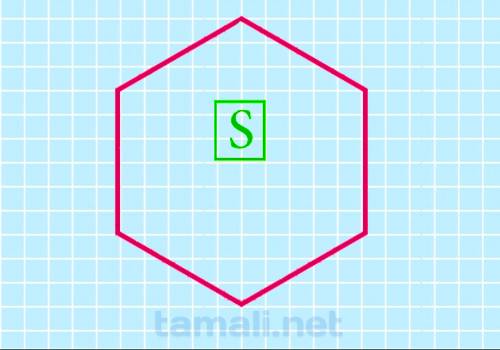
Если по условию известна только площадь, то и с этим исходным значением получится найти
периметр данной фигуры. Формула используется для этого следующая: a=sqrt(2/3*S/sqrt(3)).

Вычислив
значение «a», можно отыскать периметр, расчёт выглядит так:

P = 6*a

В данной и последующих формулах sqrt — это обозначение квадратного корня.

Площадь правильного
шестиугольника — это одна из основных числовых характеристик фигуры. С её помощью могут вычисляться
другие параметры, значение которых нужно найти в задании.

Находится по формуле: S=(3√3*a²)/2, где S
обозначается площадь правильного шестиугольника; «а» — длина его стороны.

Через короткую диагональ

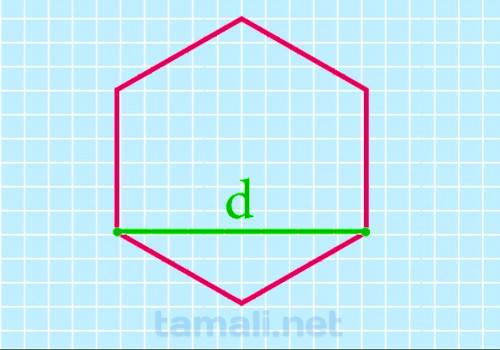
Меньшая диагональ гексагона — это величина отрезка, который соединяет одну его вершину с другой,
находящейся через один угол. Она в √3 раз больше его стороны. Отрезок отсекает в шестиугольнике
треугольник, который получается равнобедренным.
Для нахождения периметра в этом случае
используют следующую формулу:

P = 6 * (d/√3)

где d — короткая диагональ.

Через длинную диагональ

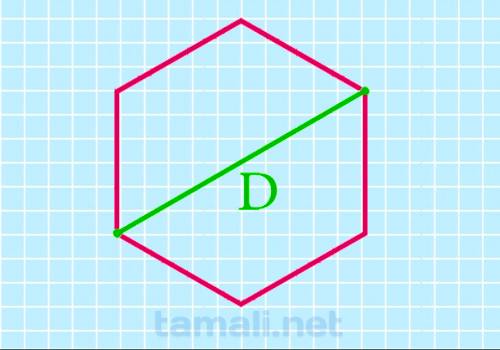
Длинная диагональ гексагона является отрезком, который проходит из одной вершины многоугольника до
противоположной. Противоположная вершина находится через два угла.

P = 3 * d

Большая диагональ шестиугольника правильной формы является диаметром описанной вокруг него окружности
и равна сумме двух его сторон. Соответственно, чтобы найти его периметр данным способом, нужно
умножить известную величину на 3.

Через радиус описанной окружности

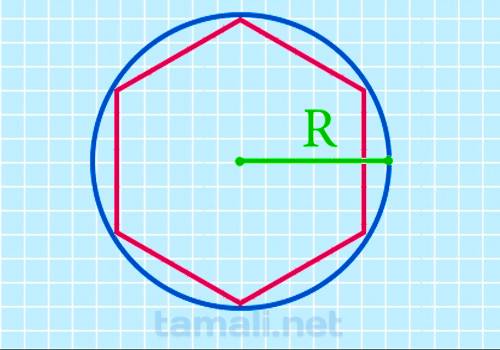
Радиус — отрезок, который идет из центра окружности к любой точке, расположенной на окружности.
Радиус описанной окружности вокруг гексагона равен длине одной его стороны.
Отсюда следует, что

P = 6 * r

где r — радиус описанной окружности.
Вокруг каждой правильной геометрической фигуры можно
описать окружность или вписать её внутрь. Правильный шестиугольник имеет только одну описанную
окружность. Периметр равен шести радиусам этой окружности.

Через радиус вписанной окружности

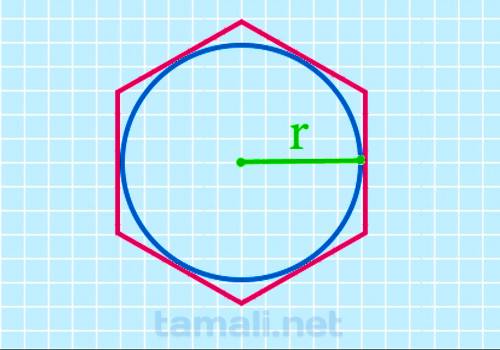
Также можно рассчитать периметр данной фигуры, если нам известен радиус вписанной в многоугольник
окружности . Искомая величина равна произведению четырёх корней из трёх и радиуса вписанной
окружности. Математическая формула выглядит так:

P = 4 * √3 * r

где r — радиус вписанной окружности.

Через сторону

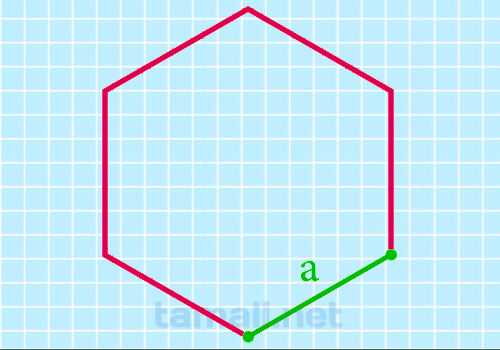
Периметр — это суммарная величина длин всех сторон плоской фигуры. Так как рассматривается
шестиугольник правильной формы, требуется измерить только одну из его сторон (здесь и далее она
обозначается как «а») и умножить на 6.

Р = 6 * a

Данный способ очень простой, используется часто, но не является единственным. Так как значение
стороны может быть неизвестно, а по условию задачи будут доступны другие исходные данные.

Найти периметр любой фигуры легко, если знать необходимые формулы и правила, а также свойства и
признаки фигур. Иногда недостаточно применять только способ сложения длин всех сторон. Для этого
может не хватать исходных данных по условию, поэтому используют формулы с участием иных терминов.
Необходимо понимать и применять аксиомы, теоремы для решения подобных и других задач. Формулы,
разобранные выше, основаны на свойствах прямоугольных треугольников. (Теорема Пифагора, синусы
углов, косинусы углов и другие.)