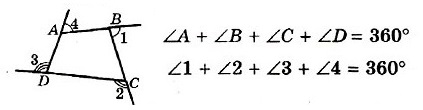Как найти периметр сторон четырехугольника, формула нахождения
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d (где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Как найти периметр четырехугольника если известны его диагонали
Диагонали четырехугольника равны 6 и 2. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,
Диагонали четырехугольника равны 57 и 8. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Это задание ещё не решено, приводим решение прототипа.
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,
Диагонали четырехугольника равны 72 и 35. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Это задание ещё не решено, приводим решение прототипа.
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,
Периметр четырехугольника
Вы будете перенаправлены на Автор24
В этой статье мы расскажем вам, как найти периметр четырехугольника, зная его стороны, а также о том, какие бывают четырёхугольники.
Для удобства на страницу добавлен онлайн-калькулятор для расчёта периметра произвольного четырёхугольника.
Четырёхугольником называют геометрический объект, состоящий из четырёх вершин, три из которых не лежат на одной прямой, и четырёх отрезков.
Различают выпуклые и невыпуклые четырёхугольники. К выпуклым относят ромбы, трапеции, параллелограммы и некоторые другие фигуры.
Расчет периметра четырехугольника
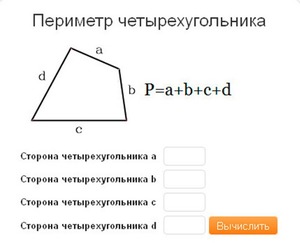
Периметр любого четырёхугольника можно рассчитать путём суммирования его сторон:
$P = a + b + c + d$, где
$a, b, c, d$ — стороны четырёхугольника.
Рассмотрим, как использовать формулу для расчёта периметра четырехугольника.
Задача
Дан четырёхугольник со сторонами $a, b, c$ и $d$, равными соответственно $3, 4, 5$ и $6$ см. Найдите его периметр.
Решение:
Для получения ответа сложим все стороны:
$P = 3 + 4 + 5 + 6 = 18$ см.
Ответ совпадает с ответом онлайн-калькулятора, а значит, решение найдено верно.
http://math-ege.sdamgia.ru/test?likes=27845
http://spravochnick.ru/calculators/perimetr_chetyrehugolnika/
Версия для печати и копирования в MS Word
1
Диагонали четырехугольника равны 6 и 2. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
2
Диагонали четырехугольника равны 57 и 8. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
3
Диагонали четырехугольника равны 72 и 35. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
4
Диагонали четырехугольника равны 7 и 3. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
5
Диагонали четырехугольника равны 6 и 13. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
6
Диагонали четырехугольника равны 28 и 45. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
7
Диагонали четырехугольника равны 13 и 50. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
8
Диагонали четырехугольника равны 34 и 43. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
9
Диагонали четырехугольника равны 34 и 7. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
10
Диагонали четырехугольника равны 25 и 46. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
11
Диагонали четырехугольника равны 26 и 40. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
12
Диагонали четырехугольника равны 11 и 6. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
13
Диагонали четырехугольника равны 57 и 30. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
14
Диагонали четырехугольника равны 55 и 16. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
15
Диагонали четырехугольника равны 37 и 42. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
16
Диагонали четырехугольника равны 78 и 11. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
17
Диагонали четырехугольника равны 6 и 24. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
18
Диагонали четырехугольника равны 55 и 37. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
19
Диагонали четырехугольника равны 12 и 10. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
20
Диагонали четырехугольника равны 3 и 1. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
21
Диагонали четырехугольника равны 3 и 12. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
22
Диагонали четырехугольника равны 22 и 47. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
23
Диагонали четырехугольника равны 13 и 41. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
24
Диагонали четырехугольника равны 34 и 29. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
25
Диагонали четырехугольника равны 8 и 4. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Периметр четырёхугольника равен сумме длин всех его сторон.
Давайте длины сторон четырехугольника будут a, b, c и d.
Мы знаем, что длины двух треугольников, образованных диагональю, равны 18 см и 22 см.
Мы можем записать периметр четырехугольника как сумму периметров двух треугольников:
a + b + c + d = 18 + 22 = 40 см
Мы также знаем, что длина диагонали равна 5 см.
Мы можем использовать эту информацию, чтобы найти длину другой диагонали, используя теорему Пифагора:
sqrt(c^2 + d^2) = 5
Затем мы можем использовать эти две уравнения, чтобы найти периметр четырёхугольника:
a + b + c + d = 18 + 22 = 40 см
и
sqrt(c^2 + d^2) = 5 см
Поэтому периметр четырёхугольника равен 40 см.
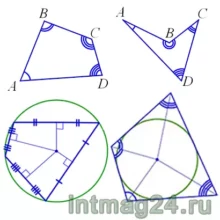
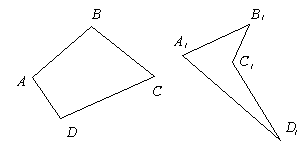
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Четырехугольники бывают выпуклые, если они расположены в одной полуплоскости относительно прямой, которая содержит одну из его сторон (ABCD) и невыпуклые (A1B1C1D1).
Если любые две противолежащие точки выпуклого четырёхугольника соединить между собой отрезком, то весь отрезок будет лежать внутри многоугольника. Для невыпуклого четырёхугольника это не выполняется (рисунок ниже).
Диагонали выпуклого четырёхугольника лежат внутри него и пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а другая внутри него, и эти диагонали не пересекаются.
Определения для четырехугольника
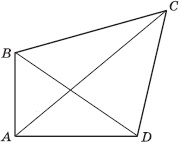
Данный четырёхугольник обозначается ABCD.
- Точки A, B, C, D называются его вершинами, а отрезки AB, BC, CD, DA – его сторонами.
- Смежные стороны – соседние стороны, имеющие общую вершину. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
- Противолежащие стороны – несмежные стороны, не имеющие общих вершин. Пары противолежащих сторон: AB и CD, BC и AD.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
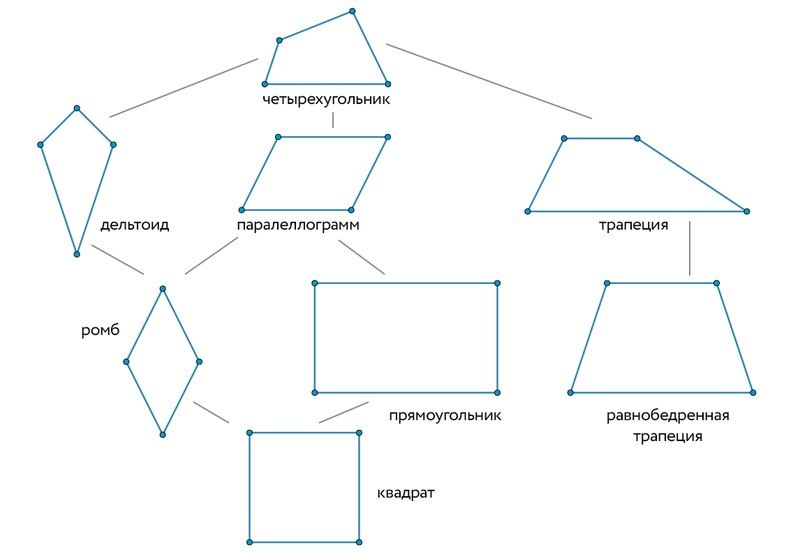
Виды четырехугольников:
Если рассмотреть схему, то каждый следующий четырехугольник обладает всеми свойствами предыдущего. Поэтому запоминать надо совсем немного.
Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Трапеции бывают: произвольная, равносторонняя, прямоугольная.
Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны. В параллелограмме:
— противоположные стороны и противоположные углы равны.
— диагонали параллелограмма делятся точкой пересечения пополам.
Соответственно, если четырехугольник обладает этими свойствами, то он является параллелограммом.
Прямоугольник — это параллелограмм, у которого все углы прямые. Прямоугольник является частным случаем параллелограмма, поэтому обладает всеми его свойствами.
Ромб — это параллелограмм, у которого все стороны равны. Ромб является частным случаем параллелограмма, поэтому обладает всеми его свойствами. В ромбе:
— противоположные углы равны,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали ромба являются биссектрисами углов.
Квадрат — это прямоугольник, у которого все стороны равны. Квадрат является частным случаем прямоугольника и частным случаем ромба, поэтому обладает всеми их свойствами. В квадрате:
— все углы равны 90 градусов,
— диагонали точкой пересечения делятся пополам,
— диагонали взаимно перпендикулярны,
— диагонали являются биссектрисами углов,
— диагонали равны.
Свойства углов четырехугольника
- Сумма углов четырёхугольника равна 360°
- Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
Свойства сторон четырехугольника
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
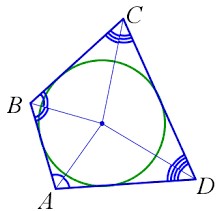
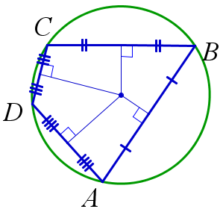
Четырехугольник и окружность
Четырехугольник вокруг окружности.
- Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
- В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны (AB+CD=AD+BC).
- Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
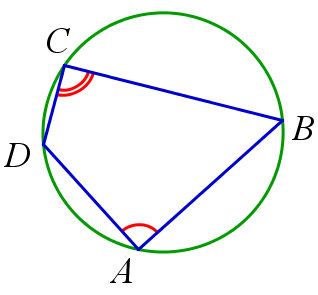
Четырехугольник внутри окружности.
- Вписанный четырёхугольник — это четырёхугольник, все вершины которого лежат на одной окружности. Эта окружность называется описанной.
- Вокруг четырёхугольника можно описать окружность, если сумма двух его противоположных углов равна 180°.
- Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (AC*BD=AB*CD+AD*BC).
Частные случаи:
- Параллелограмм, вписанный в окружность – это прямоугольник, центр окружности совпадает с точкой пересечения диагоналей.
- Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
- Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Диагонали четырехугольника
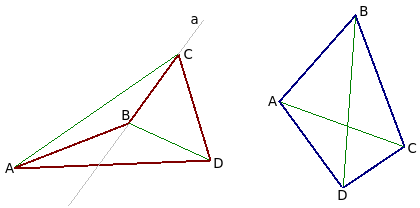
- Диагонали выпуклого четырёхугольника пересекаются в одной точке.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Периметр и площадь четырехугольника
Периметр четырёхугольника равен сумме длин всех его сторон: где a, b, c, d – длины сторон четырёхугольника.
Площадь произвольного выпуклого четырёхугольника можно найти по формуле: где d1 и d2— диагонали четырёхугольника, a — угол между диагоналями.
Площадь вписанного четырёхугольника может быть вычислена по формуле: 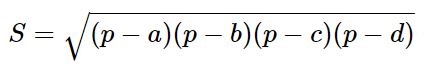
Площадь описанного четырёхугольника равна произведению его полупериметра на радиус вписанной окружности:
Как найти периметр четырёхугольника
Четырехугольник представляет собой геометрическую фигуру, обладающую четырьмя сторонами и таким же количеством углов. Независимо от типов четырехугольников, для подсчета их периметра существует единый подход. Но у него есть свои разновидности, которые вытекают из типа четырехугольника.
Вам понадобится
- Знать все стороны четырехугольника.
Инструкция
Для того, чтобы рассчитать периметр четырехугольника ABCD со сторонами AB, BC, CD и DA, нужно сложить вместе каждую из его его сторон:
P = AB+BC+CD+DA, где
P — периметр четырехугольника.
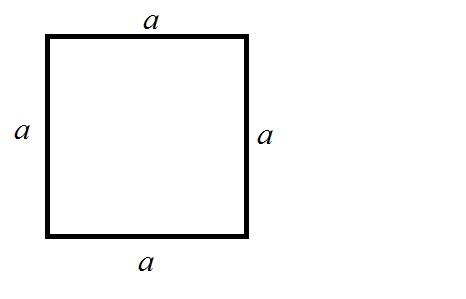
Если дан квадрат со стороной a (у квадрата все стороны равны), то его периметр будет вычислен таким образом:
P = 4*a.
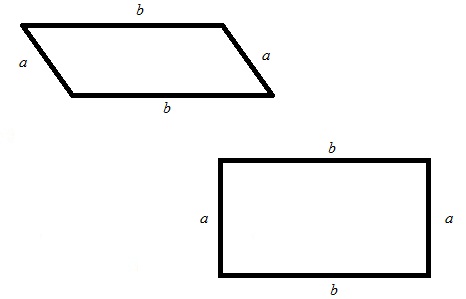
Если дан прямоугольник или параллелограмм (у них обоих противолежащие стороны равны), то его площадь будет рассчитываться так:
P = 2*(a+b), где a и b — стороны прямоугольника/параллелограмма.
Источники:
- как найти периметр abcd
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

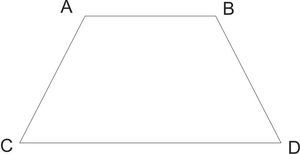

 Данный четырёхугольник обозначается ABCD.
Данный четырёхугольник обозначается ABCD.