Let’s learn how to find the Perimeter and Area of Mixed Figures. We will get mixed figures with the combination of several shapes. The mixed figures may be a combination of any shapes like triangle and square, square and rectangle, triangle and pyramid, etc. This article completely explains the formulas for perimeter and area of the different mixed figures, steps on how to find the area and perimeter of combined figures. 9th Grade Math students can get different examples with their explanations step by step with relevant images for better understanding.
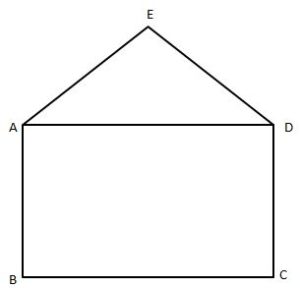
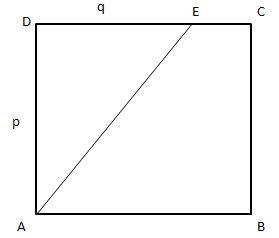
When we add different shapes to form a combined shape, we can see the different shapes. The shape which is the combination of different shapes is known as mixed figures. Below is an example of a mixed figure.
From the above figure, ABCD is a rectangle and ABE is a triangle. By combining both figures, we got a new figure ABCDE.
How to find Perimeter and Area of Mixed Figures?
Follow the below procedure to find the perimeter and area of mixed figures. The step-by-step process to find the area and perimeter is given separately below.
How to Find Area of Mixed Figures?
Step 1: Firstly, find out the shape.
Step 2: If you identify the individual shapes then find the area separately.
Step 3: Then, add the total area to find the complete answer.
Step 4: Finally, note down the answer in square units.
Also, check:
- Perimeter and Area of Irregular Figures
- Perimeter and Area of Square
- Perimeter and Area of Rectangle
How to Find the Perimeter of Mixed Figures?
The perimeter of the mixed figures can find by adding the total side lengths of the shape. If rectangle and square are two shapes then add the lengths of four sides.
Perimeter and Area of Mixed Shapes Examples
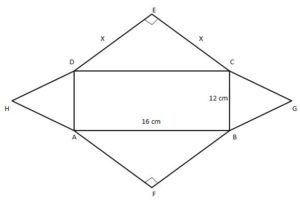
Example 1: The length and breadth of a rectangular field are 16 cm and 12 cm respectively. Two right-angled isosceles triangles are constructed outside the rectangular field, with the longer sides as the hypotenuses. On the 12 cms sides of the rectangular field, two equilateral triangles are constructed outside. Find the total area and perimeter of the figure.
Solution: The figure consists of the following.
(i) The rectangular field ABCD, whose area = 16 × 12 cm2 = 192 cm2
(ii) Two equilateral triangles ADH and BCG. For each, area = √3/4 × 12 cm2 = 3 √3 cm2
(iii) Two isosceles right-angled triangles CDE and ABF, whose areas are equal.
According to Pythagoras’ theorem, if CE = ED = x then x2 + x2 = (16)2 cm2 or 2x2 = 256 cm2. Therefore, x = 8√2 cm.
Therefore, the area of the ∆CDE = 1/2 CE × DE = 1/2 x2 = 1/2 (8√2)2 cm2 = 64 cm2
Therefore, area of the figure = area of the rectangular field ABCD + 2 × area of the ∆BCG + 2 × area of the ∆CDE
= (192 + 2 × 3 √3 + 2 × 64) cm2 = 1920√3 cm2 =
The perimeter of the figure = length of the boundary of the figure
= AF + FB + BG + GC + CE + ED + DH + HA
= 4 × CE + 4 × BG
= (4 × 8√2 + 4 × 12) cm
= 93.12 cm
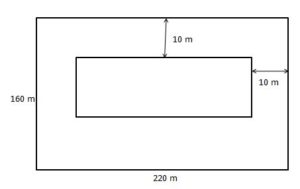
Example 2. The dimension of a field is 220 m × 160 m. The field is to be converted into a garden after some days, leaving a path 10 m broad around the garden. Find the total cost of making the new garden if the cost per square meter is Rs 24.
Solution:
For the garden, length = (220 – 2 × 10) m = 200 m, and Breadth = (160 – 2 × 10) m = 140 m.
Therefore, area of the garden = 200 m × 140 m = 28000 m2.
Therefore, the total cost of making the garden = 28000 × Rs 24 = 672000
Example 3. A square-shaped piece of paper is made into two pieces along a line joining a corner and a point on an opposite edge. If the ratio of the areas of the two pieces is 6:2, find the ratio of the perimeters of the smaller piece and the original piece of paper.
Solution:
Let ABCD be the square-shaped piece of paper. Let its side measure a unit.
It is cut along AE. Let DE = q units
Area of the ∆EDA = 1/2 (AD × DC) = 1/2 pq square units.
Area of the square ABCD = p2 square units.
According to the question,
(Area of the quadrilateral ABCE/ Area of the ΔEDA) = 6/2
(Area of the quadrilateral ABCE/ Area of the ΔEDA) + 1 = 8/2
(area of the quadrilateral ABCE + area of the ΔEDA)/area of the ΔEDA = 8/2
(Area of the quadrilateral ABCD/ Area of the ΔEDA) = 4
p2/(pq/2) = 4
2p/q = 4
p = 2q
q = p/2
According to Pythagoras’ theorem,
AE2 = AD2 + DE2
Therefore, AE2 = p2 + q2
= p2 + (p/2)2
= p2 + 1/4 (p2)
= 5/4 (p2)
Therefore, AE2 = √5/2p.
Now, the perimeter of the ΔEDA/perimeter of the square ABCD = (ED + AD + AE)/4p
= (p/2 + p + √5p/2)/4p
= [(3+√5)p/2]/4p
= (3+√5)/8
= (3+√5) : 8.
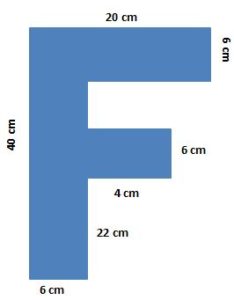
Example 4. From a 40 cm × 20 cm board having an F-shaped block is cut out as given in the below figure. What is the area of the face of the remaining board? Also, find the length of the boundary of the board or block.
Solution:
The given figure is the combination of three rectangular blocks.
Therefore, area of a face of the block = 40 × 6 cm2 + 6 × 4 cm2 + 14 × 6 cm2
= 240 cm2 + 28 cm2 + 84 cm2
= 352 cm2
Area of a face of the uncut board = 40 × 20 cm2
= 800 cm2
Therefore, the area of the face of the remaining board = 800 cm2 – 352 cm2 = 448 cm2
Required length of the boundary = (40 + 6 + 22 + 4 + 6 + 4 + 6 + 14 + 6 + 20) cm = 128 cm
Пошаговое объяснение:
если это квадрат то нужно длину его стороны умножить на 4
А если это. прямоугольник нужно сумму его ширины и длины умножить на два.
а чтобы найти периметр паллелограма нужно сумму двух непаралельных сторон умножить на два
А мне картинка показалась до боли похожей на чемодан, положенный на бок. Давайте вернём его в вертикальное положение, а потом сопоставим два изображение. На одном мой чемодан будет с утопленной ручкой, как и положено при длительном его хранении в кладовке. А во втором случае мы ручку вытащим, как будто вновь объявили карантин и мы засобирались в Крым на самоизоляцию.
На сколько я вижу, ширина ручки в подобной задаче не имеет никакого значения, если её направляющие параллельны и исправно функционируют. Периметр чемодана увеличивается, но это зависит от того, на сколько высоко мы ручку вытащим. И не важно, в качестве выступа образуется квадрат или прямоугольник.
Таким образом, если периметр у фигуры был равен 100, то к нему нужно будет добавить только удвоенную высоту выступа. Но, поскольку в условии задачи говорится, что выступающая фигура является квадратом с периметром 40, то нам нужно прибавить всего-то две стороны, каждая из которых равна четверти от сорока. В итоге формула для расчётов мне видится следующей:
P = P(бол.) + 2*(P(мал)/4)
или ещё проще:
P = P(бол.) + P(мал)/2
Что же получается при подстановке указанных в задании значений? P = 100 + 40/2 = 100 + 20 = 120.
Понятное дело, что все вычисления действительны для случаев подобных изображённому на рисунке, когда малый квадрат полностью лежит на одной из сторон большого. При сдвиге за край общий периметр станет увеличиваться и будет зависеть от степени сдвига.
Для таких фигур, как квадраты, прямоугольники и круги, вы можете использовать формулы для расчета периметра, когда вы знаете только одно или два измерения. Когда вам нужно найти периметр фигуры, составленной из комбинации других фигур, сначала может показаться, что вам не дано достаточно размеров. Однако вы можете использовать данные размеры, чтобы рассчитать другие необходимые размеры, а затем найти периметр всей фигуры.
-
Убедитесь, что вы добавили только длины вдоль всей объединенной или неправильной формы — не используйте полные периметры всех меньших фигур, на которые вы разделили форму.
Нарисуйте прямые линии, чтобы разделить комбинированную или неправильную форму на правильные формы, которые вы знаете, как найти периметр, такие как прямоугольники, прямоугольные треугольники и полукруги.
Рассчитайте измерения недостающего периметра из данных измерений. Например, если у вас есть фигура, состоящая из прямоугольника и полукруга, вычислите периметр круга на основе размеров прямоугольника. Диаметр круга равен длине стороны прямоугольника, к которому он прикреплен, поэтому, если эта длина равна 4 дюймам, например, используйте формулу для периметра круга и разделите на два, чтобы найти периметр полукруга — 4 x пи / 2 = 6, 28 дюйма. Если ваша разделенная фигура включает в себя прямоугольный треугольник и вы знаете длину двух сторон треугольника, рассчитайте длину третьей стороны с помощью теоремы Пифагора.
Добавьте длины всех сегментов вдоль внешней части фигуры, чтобы найти периметр. Например, для формы прямоугольника и полукруга добавьте длины трех сторон прямоугольника и периметр полукруга, чтобы найти общий периметр фигуры. Если вы не можете разделить неправильную форму на правильную форму, вы должны знать длину каждого сегмента периметра. Сложите все длины вместе, чтобы найти периметр.
подсказки
Ответ:
32 см
Пошаговое объяснение:
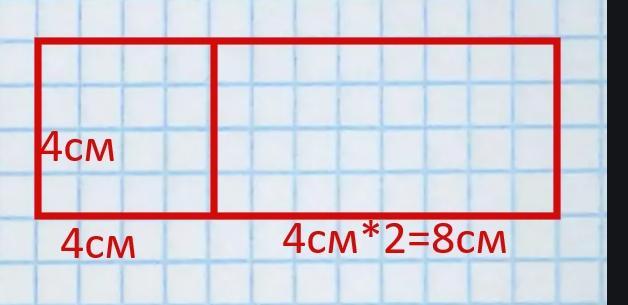
Обратим внимание на то, что «Ширина прямоугольника равна ширине
квадрата».
Это значит, что квадрат «приставлен» именно к стороне, которая является шириной. И вот эта ширина, а следовательно и сторона квадрата = 4 см. (см рисунок)
Тогда
Ширина прямоугольника = 4см (по условию)
Длина прямоугольника = 4см*2 = 8см («длина прямоугольника
вдвое больше его ширины»)
Тогда из рисунка видно, что
ширина фигуры а = 4см,
длина фигуры b = 4см + 8см = 12 см
Периметр комбинированной фигуры
P = 2(a+b)
P = 2(4cм + 12cм) = 2*16см = 32см
ответ
Периметр комбинированной фигуры 32см
Приложения: