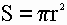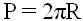Периметр круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Периметр круга
Чтобы посчитать периметр круга просто воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
его радиус ?
Ответ:
0
Каков периметр круга (L) если его радиус r ?
Формула
L = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
его диаметр ?
Ответ:
0
Каков периметр круга (L) если его диаметр d?
Формула
L = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная его площадь
Чему равен периметр круга если
его площадь ?
Ответ:
0
Каков периметр круга (L) если его площадь S?
Формула
L = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 8 см2, то его периметр ≈ 10 см.
См. также
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
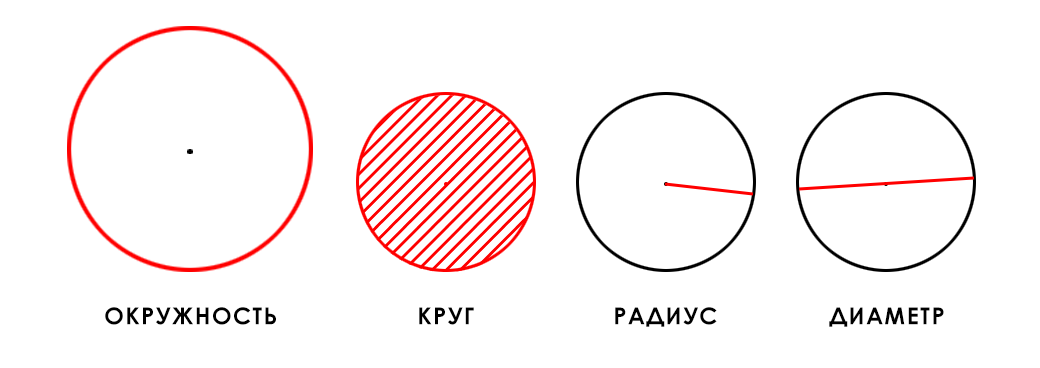
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
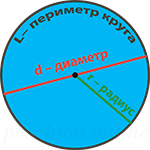
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
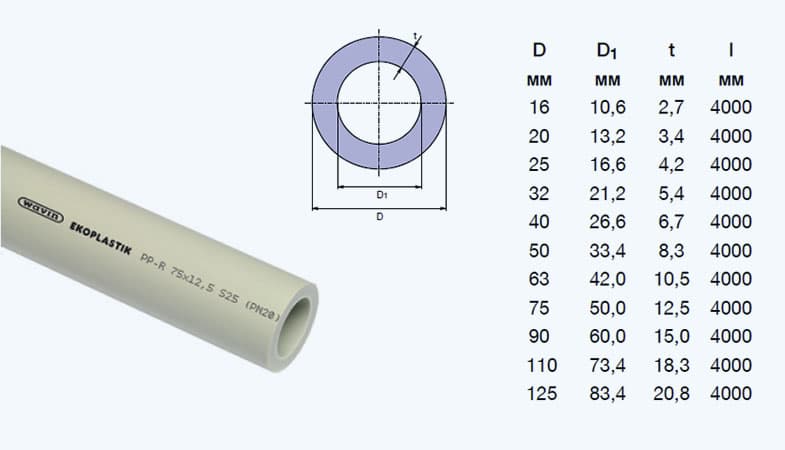
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5. Получаем 14400,04.
- И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.
Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π = 3.14159…
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. Наш онлайн калькулятор вычисляет периметр круга по значению длины его радиуса.
Формула для вычисления длины окружности
$S = 2 pi r$, где:
r — радиус окружности
Остались вопросы?
Здесь вы найдете ответы.
Периметр круга – что это такое?
Периметр круга, также называемый длиной окружности, представляет собой
число, получаемое в результате умножения его радиуса на два Пи, либо путем
перемножения между собой его диаметра и числа Пи. Формула, используемая
для расчета периметра круга, представлена в следующем виде:
L = d*π = 2*r*π.
Расшифровка обозначений:
d — диаметр круга,
r — его радиус,
π — это величина, которая является константой, выражающей отношение длины
окружности к ее диаметру. Ее значение постоянно равно 3,14.
Каким способом производится вычисление периметра круга?
Под определением «расчет периметра круга» подразумевается процедура,
направленная на установление длины окружности, ограничивающей его. В
случае, когда длина радиуса круга является известной величиной, длина
окружности может быть вычислена с применением приведенной ниже формулы:
l=2*π*r,
в ней радиус круга обозначен как r.
Под радиусом окружности подразумевается отрезок, который соединяет центр
окружности с любой из множества точек, находящихся на ней.
Значение длины окружности также может быть вычислено, если диаметр круга
известен. С этой целью нужно произвести умножение ее диаметра (d) на число
Пи (π). В этом случае следует пользоваться формулой:
l=πd.
Если раскрывать такое понятие, как «диаметр окружности», то стоит
отметить, что им является отрезок, проходящий через ее центр и соединяющий
две любые точки этой окружности.
Число Пи (π) является математической постоянной, рассчитываемой как
отношение длины окружности к величине ее диаметра. Оно равно 3,14.
В квадрат, длина стороны которого равна 20 см, вписан круг. Как вычислить
периметр данного круга?
Периметр круга представлен величиной, равной длине окружности, которая
ограничивает его. Это значит, что данная величина может быть рассчитана по
формуле:
P = L = d*π.
В описанном в задании случае сторона квадрата, в который вписан круг,
выступает в роли его диаметра. Это дает основания для расчета периметра
круга следующим образом:
P = 20 * 3,14 = 62,8 см.
Ответ: Периметр круга, который вписан в квадрат, имеющий сторону 20 см,
равен 62,8 см.
Периметр круга равен 30 π. Как можно вычислить длину его окружности?
Длина окружности представляет собой произведение, полученное в результате
умножения ее диаметра (D) на число Пи (π): L = π*D = 30*π. В данном случае
длина окружности – это ее периметр. Из этого следует, что диаметр
окружности D равен 30.
Известно, что длина одного круга равна 3,6 дм. Каким образом можно
определить длину второго круга, если известно то, что диаметр первого круга
в три раза меньше диаметра второго?
Решение поставленной задачи следует начинать с расчета длины первого
круга. Для этого число Пи, равное 3,14, нужно умножить на два, а затем
полученное значение также умножить на длину радиуса круга. Формула,
используемая при этом, выглядит так:
L=2пR.
Принимая во внимание тот факт, что диаметр второго круга в три раза
превышает диаметр первого из них, то можно с уверенностью говорить о том,
что его радиус также будет троекратно превышать радиус первого круга. Это
означает, что формула, применяемая для расчета длины второго круга, будет
выглядеть так:
L=2п*3R
2п*3R/2пR=3.
Подставив в формулу величины, приведенные в задании, можно получить
следующий результат:
3,6*3=10,8 дм.
Ответ: Длина второго круга равна 10,8 дм.
Каким образом можно высчитать длину круга, если известно, что его площадь
составляет 25 дм.кв?
В задании указано, что площадь круга составляет 25 дм.кв. Это значит, что
произведение числа Пи и радиуса круга, возведенного в квадрат, равно 25
дм.кв. Из этого следует, что радиус данного круга равен величине,
полученной в результате деления 5 на квадратный корень из числа Пи (r =
5/√π). На основании этого можно сделать вывод о том, что длина круга может
быть высчитана по следующей формуле:
L = 2πr = 10√π дм.
В результате получается число, приблизительно равное 17,72 дм.
Ответ: Длина круга равна примерно 17,72 дм.
Как высчитать диаметр круга, длина которого равна 40 Пи см?
Формула, которая предназначена для расчета длины круга выглядит так:
L = πD.
По сути, это произведение числа Пи и диаметра круга.
В случае, который описан в задании, длина круга равна 40 Пи см, а это
значит следующее:
πD = 40π.
Число Пи сокращается в обеих частях получившегося уравнения, и в итоге
получается, что диаметр круга равен 40 см:
D = 40 cм.
Каким образом следует рассчитывать площадь круга, если известно, что его
длина составляет 19,1 м?
Располагая информацией о длине круга, можно вычислить его радиус. Это
можно сделать на основании приведенной ниже формулы:
r = L/(2*π) = 19,1:(2*3,14)=3 м.
Таким образом удалось установить, что радиус круга равен 3 м.
Теперь, зная длину радиуса круга, можно произвести расчет его площади по
формуле:
π*r2 = 3,14*3*3 = 28,26 м².
Ответ: Площадь круга равна 28,26 м. кв.
Величина длины круга известна. Она составляет 26 см. Как можно рассчитать
его площадь и диаметр?
При расчете таких показателей, как площадь и диаметр круга, следует
использовать его длину. Она обозначается как с и равна 26 см. Согласно
формуле вычисления длины круга, она равна произведению 2 Пи и радиуса
круга, либо Пи и его диаметра (с=2πr или c=πd). Исходя из этого, диаметр
круга можно найти путем деления длины круга на число Пи:
d=c/π
В данном случае d=26/3,14=8,28 см.
Теперь, когда все необходимые для вычисления площади круга параметры
известны, можно перейти непосредственно к ее расчету:
S=2πr²=2*3,14*8,28*8,28=53,7 см².
Как выглядит формула, используемая для расчета длины окружности по радиусу?
В целях выполнения вычисления длины окружности по радиусу (r) следует
произвести умножение величины, выражающей его значение, на два Пи. При
этом используется следующая формула:
P=2πr.
Чему равна длина окружности, диаметр которой 4 м?
При расчете длины окружности используется формула, которая имеет следующий
вид:
L = π*D.
Согласно данной формуле, для того чтобы вычислить, чему равна длина
окружности, необходимо произвести умножение ее диаметра на число Пи,
равное 3,14.
Подставляя в приведенную выше формулу числа, указанные в задании, можно
произвести расчет длины окружности, которая будет равна:
3,14*4 = 12,56 м.
Ответ: Длина окружности диаметром в 4 м равна 12,56 м.
Какому числу будет равна длина окружности круга при условии, что его площадь
равна Пи м. кв?
Площадь круга высчитывается при помощи формулы:
S=πR².
В данном конкретном случае указано, что площадь равна Пи м. кв. (S=π).
Исходя из вышеизложенного, можно произвести расчет величины радиуса,
которая будет равна отношению корня квадратного из числа Пи и числа Пи:
R=√π/π=1.
Теперь можно приступить к вычислению непосредственно длины окружности,
используя следующую формулу:
C = 2πR = 2π⋅1 = 2π.
Ответ: Длина окружности круга площадью Пи кв. м равна 2 Пи.
Чему будет равна длина круга диаметром 16 см?
При расчете длины круга следует брать за основу формулу, которая
предполагает умножения числа Пи, равного 3,14, на диаметр окружности
круга. Если говорить о конкретном случае, упомянутом в задании, то расчет
длины окружности будет выглядеть следующим образом:
L=16 см*3,14=50,24 см.
Ответ: Длина круга, диаметр которого равен 16 см, составляет 50,24 см.
Диаметр круга составляет 5,8 дм. Какому числу будет равна длина этого круга?
Длина окружности рассчитывается с применением формулы, составными
элементами которой являются диаметр (d) и число ПИ, равное 3,14. Для
вычисления длины окружности упомянутые величины следует перемножить:
L=π*d=3,14*5,8=18,212 дм.
Ответ: Круг диаметром 5,8 дм имеет длину окружности, равную 18,212 дм.
Известно, что круг имеет диаметр 18 м. Как вычислить длину этого круга по
диаметру?
Если диаметр круга является известной величиной, то ее вполне достаточно,
для того чтобы произвести расчет длины данного круга. С этой целью следует
использовать формулу, приведенную ниже:
l = 2πr = πd.
Если подставить в данную формулу величины, заданные в вопросе, то можно
получить следующий результат:
l = 3,14*18 = 56,52 м.
Ответ: Длина круга, диаметр которого равен 18 м, составляет 56,52 м.
Формулы круга и окружности
- Формула площади круга
- Формула периметра круга (длины окружности)
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Формула площади круга
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади круга выражается числом заключающихся в него квадратных единиц.
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
Формула периметра круга (длины окружности)
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр круга равен произведению радиуса на два пи (3.1415).
P — Периметр круга (длина окружности)
π — число пи (3.1415)
r — радиус круга (окружности)
Длина окружности
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).
Ответ: 12,56 см 2 .
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 · | 7 2 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см 2 ). |
| 4 |
Ответ: 38,465 см 2 .
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
Периметр круга
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
Каков периметр круга (L) если его радиус r ?
Формула
L = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
Каков периметр круга (L) если его диаметр d?
Формула
L = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная его площадь
Чему равен периметр круга если
Каков периметр круга (L) если его площадь S?
Формула
L = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 8 см 2 , то его периметр ≈ 10 см.
http://izamorfix.ru/matematika/planimetriya/dlina_okruj.html
http://poschitat.online/perimetr-kruga
Как определить периметр круга
Периметром плоской геометрической фигуры называется суммарная длина всех составляющих ее сторон. У круга такая сторона всего одна, и ее протяженность обычно называют длиной окружности, а не периметром. В зависимости от известных параметров круга вычислять эту величину можно разными способами.

Инструкция
Для измерения периметра круга на местности используйте специальное устройство — курвиметр. Чтобы узнать с его помощью длину окружности, агрегат нужно просто прокатить по ней колесом. Такие же приборы, но гораздо меньших размеров, используются и для определения длины любых кривых линий, включая окружности, на чертежах и картах.
Если нужно вычислить длину окружности (L) по известному диаметру (d), умножьте его на число Пи (3,1415926535897932384626433832795…), округлив количество знаков до нужной степени точности: L=d*π. Так как диаметр равен удвоенному радиусу (r), если известна эта величина, добавьте в формулу соответствующий множитель: L=2*r*π.
Зная площадь круга (S), тоже можно вычислить длину окружности (L). Соотношение и этих двух величин выражается через число Пи, поэтому удвойте квадратный корень из произведения площади на эту математическую константу: L = 2*√(S*π).
Если известна площадь (s) не всего круга, а лишь сектора с заданным центральным углом (θ), то при вычислении длины окружности (L) исходите из формулы предыдущего шага. Если угол выражен в градусах, площадь сектора будет составлять θ/360 от общей площади круга, которую можно выразить формулой s*360/θ. Подставьте ее в приведенное выше равенство: L = 2*√((s*360/θ)*π) = 2*√(s*360*π/θ). Однако чаще для измерения центрального угла используют не градусы, а радианы. В этом случае площадь сектора будет составлять θ/(2*π) от общей площади круга, а формула вычисления длины окружности приобретет такой вид: L = 2*√((s*2*π/θ)*π) = 2*√(s*2*π²/θ) = 2*π*√(2*s/θ).
Аналогичные пропорции применяйте и при вычислении длины окружности (L) по известным длине дуги (l) и соответствующему ей центральному углу (θ) — в этом случае формулы будут проще. При центральном угле, выраженном в градусах, используйте такое тождество: L = l*360/θ, а если он дан в радианах, формула должна быть такой: L = l*2*π/θ.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.