Объем, площадь и периметр прямоугольного параллелепипеда — онлайн
Объем, площадь и периметр прямоугольного параллелепипеда.
Прямоугольный параллелепипед — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником.
Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.
Объём прямоугольного параллелепипеда можно найти по формуле:
V=abc;
Площадь поверхности прямоугольного параллелепипеда равна:
S=2(ab+bc+ac);
Периметр параллелепипеда рассчитывается по следующей формуле:
P = 4a + 4b + 4c;
Объем, площадь и периметр прямоугольного параллелепипеда — калькулятор онлайн
Сторона a:
Сторона b:
Сторона c:
Найти:
V – Объем
S – Площадь
P — Периметр
Итого :
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн — косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
При помощи нашего калькулятора вы легко сможете узнать периметр прямоугольного параллелепипеда.
Для того что бы вычислить периметр параллелепипеда необходимо знать длину его ребер a,b и c сходящихся к одной точки. Если нам известны указанные величины, для нас не составит труда вычислить периметр.
Периметр параллелепипеда рассчитывается по следующей формуле:
P=4a+4b+4c
Где P – периметр, a,b и c – длина ребер параллелепипеда.
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
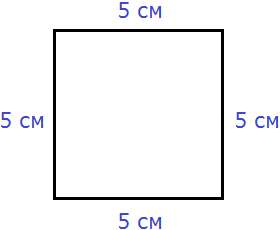
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
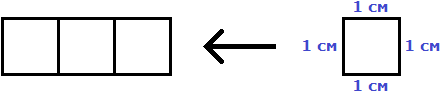
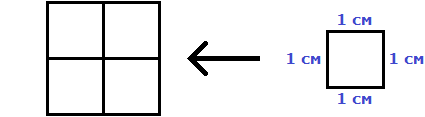
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
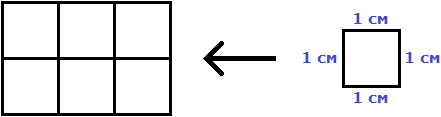
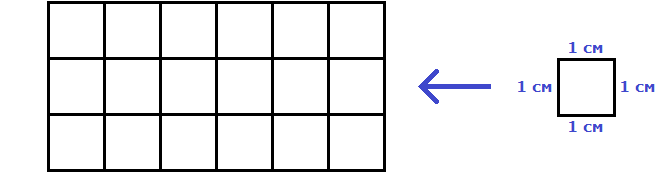
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
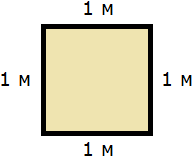
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
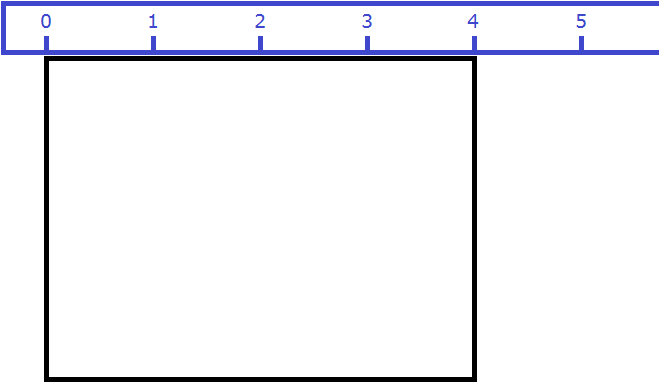
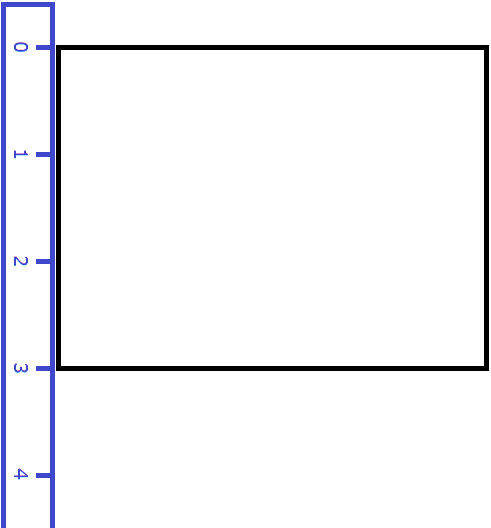
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
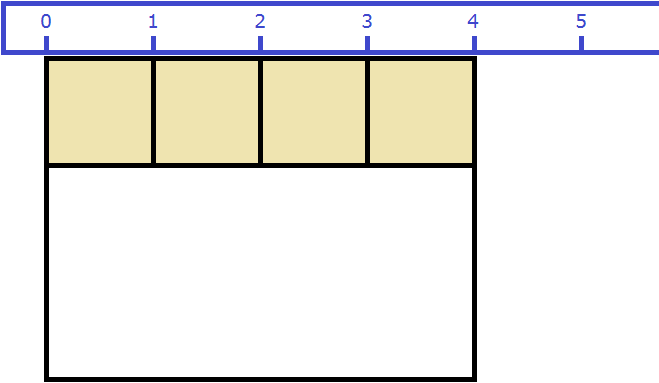
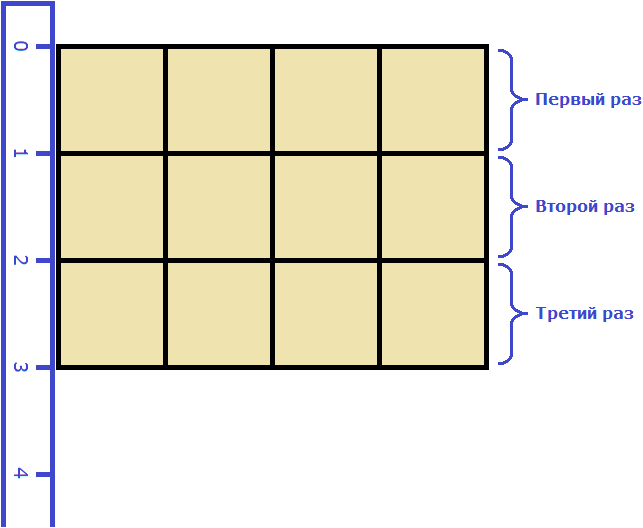
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
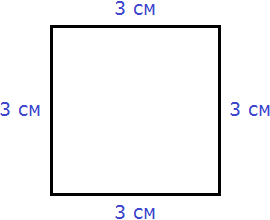
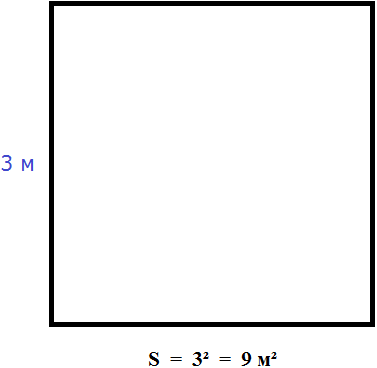
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
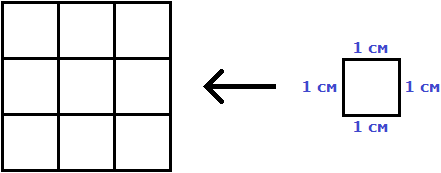
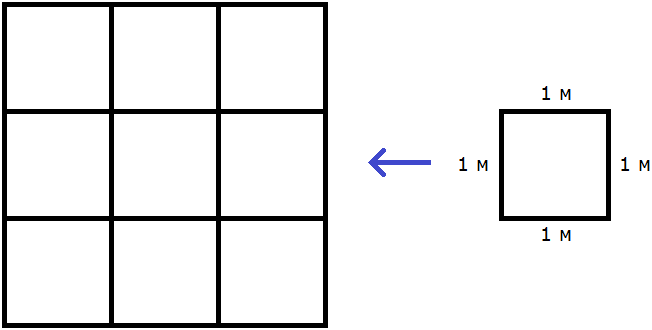
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
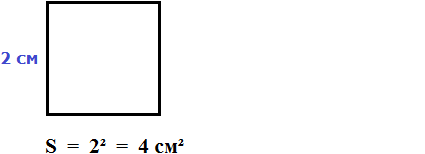
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
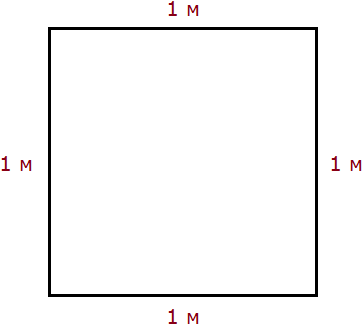
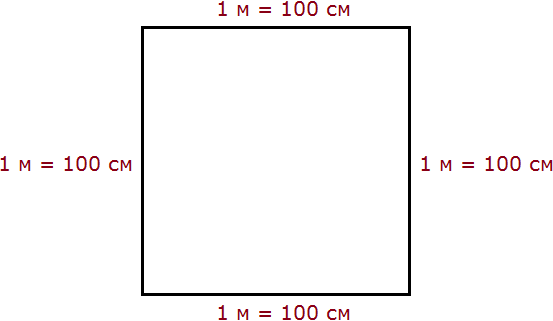
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
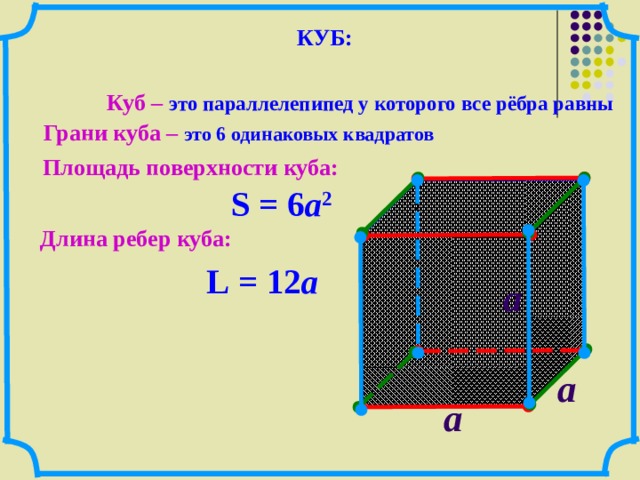
Прямоугольный параллелепипед и куб
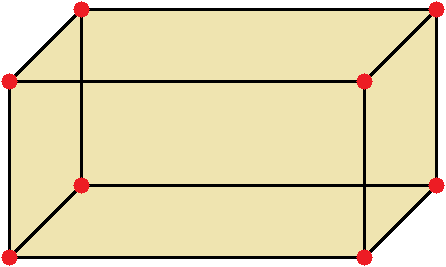
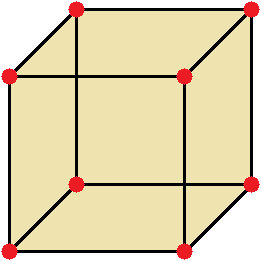
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
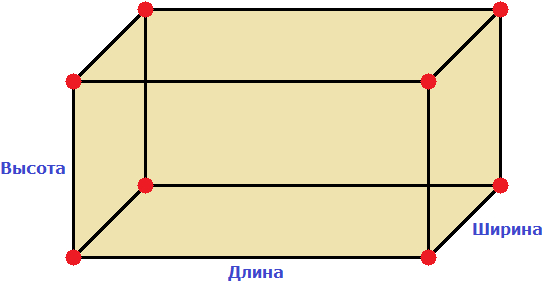
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
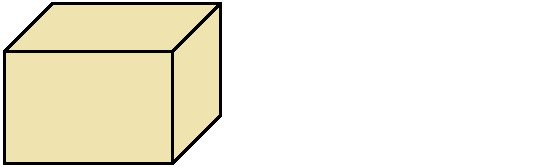
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
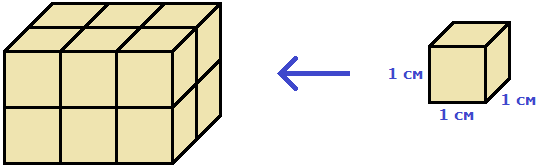
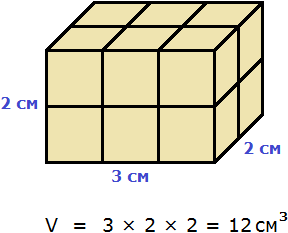
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
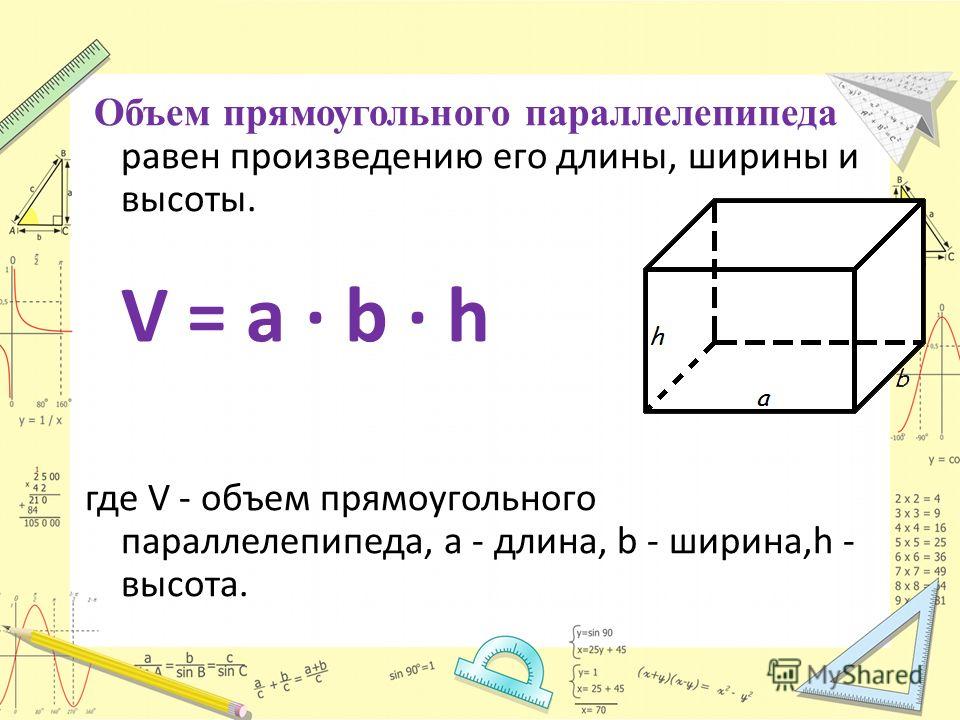
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
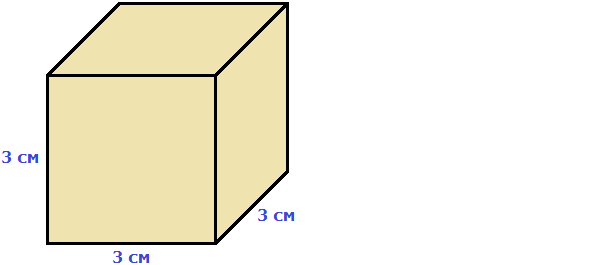
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
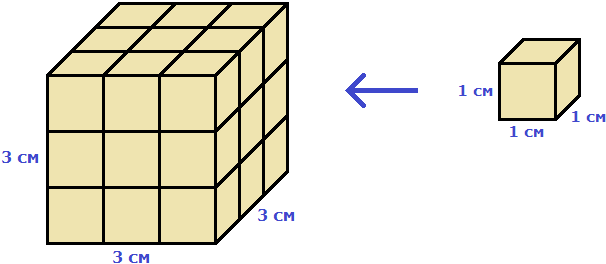
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
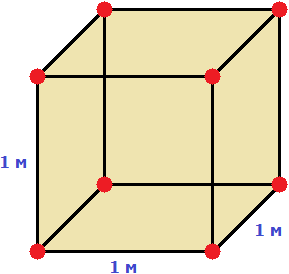
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
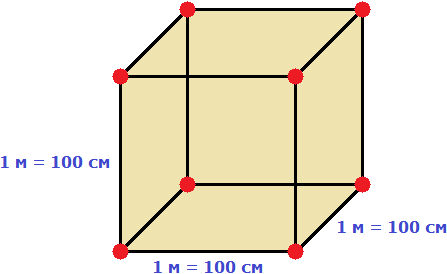
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
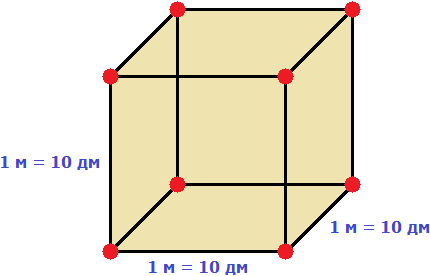
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
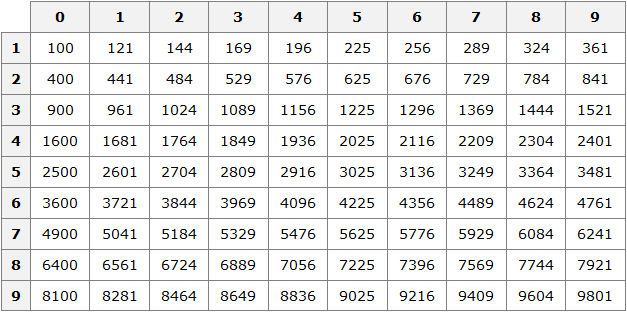
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
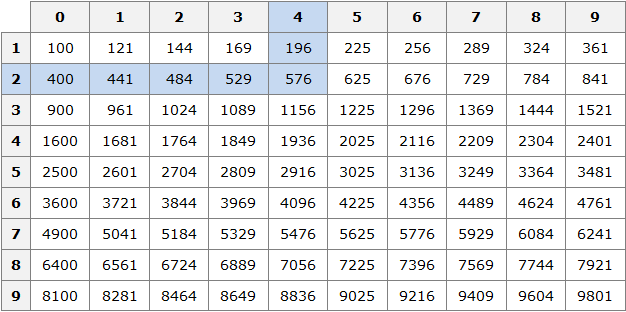
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
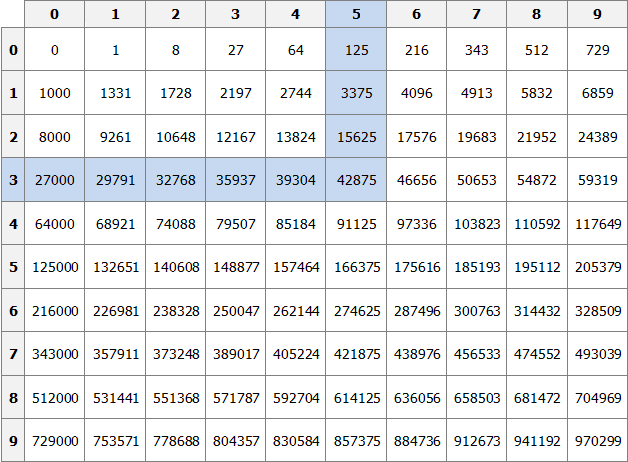
Таблица кубов
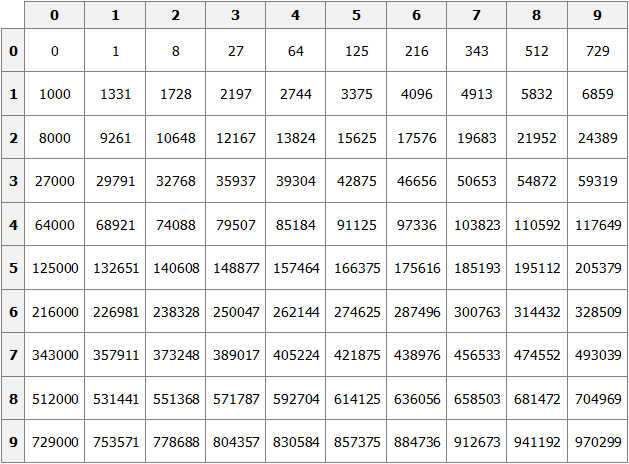
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет 
Решение
a — длина
b — ширина
c — высота
a = 42 м
b = 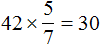
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Производная в задачах на прямоугольный параллелепипед 10 класс онлайн-подготовка на Ростелеком Лицей
Тема: Производная
Урок: Производная в задачах на прямоугольный параллелепипед
1. Задача 1 на прямоугольный параллелепипед
Рассматриваются всевозможные прямоугольные параллелепипеды, основания которых квадраты, а каждая из боковых граней имеет периметр . Найти среди них параллелепипед с наибольшим объемом и вычислить его объем.
Решение.
Напомним, прямоугольным называется параллелепипед, у которого в основании лежит прямоугольник, и боковые ребра перпендикулярны к плоскости основания.
Нам важны три измерения этого параллелепипеда. Так как в основании лежит квадрат, то его стороны обозначим через , третье измерение параллелепипеда обозначим через (см. рис. 1).
Рис. 1. Прямоугольный параллелепипед и его измерения.
Объем любого прямоугольного параллелепипеда – это произведение трех его измерений. Надо найти такой параллелепипед, чтобы его объем был максимальным (смотрим прямоугольный параллелепипед формулы), то есть
. Между и есть связь. Сказано, что или . Заметим, что , .
Мы бы могли решить эту задачу, если бы функция зависела от одной переменной, а она зависит от двух переменных и . Одну из них можно выразить через связь . Отсюда . Подставим полученное выражение в функцию: . Теперь задачу можно свести к типовой задаче: найти на отрезке .
1) Найдем производную
– критические точки.
Достаточно сравнить значение функции на концах отрезка и в тех критических точках, которые попадают на данный отрезок. Продемонстрируем, что точка — точка максимума. Для этого проанализируем знак производной (см. рис.2).
Рис. 2. Интервалы знакопостоянства производной.
Найдем значение функции в точках:
Если , тогда . Найдем объем .
Итак, мы искали такой прямоугольный параллелепипед, в основании которого лежит квадрат, и периметр боковой грани равен 6.
2. Задача 2 на прямоугольный параллелепипед
Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого из которых равен , а основаниями являются квадраты. Найти среди них параллелепипед с наименьшим периметром боковой грани и вычислить этот периметр.
Рис. 3. Прямоугольный параллелепипед и егобоковые грани и измерения.
Решение.
Так как в основании параллелепипеда – квадрат, то одна его сторона равна и вторая – , боковое ребро – (см. рис.3). Известно, что объем этих параллелепипедов -. Надо найти параллелепипед с наименьшим периметром боковой грани. Периметр боковой грани равен . Этот периметр должен быть наименьшим: .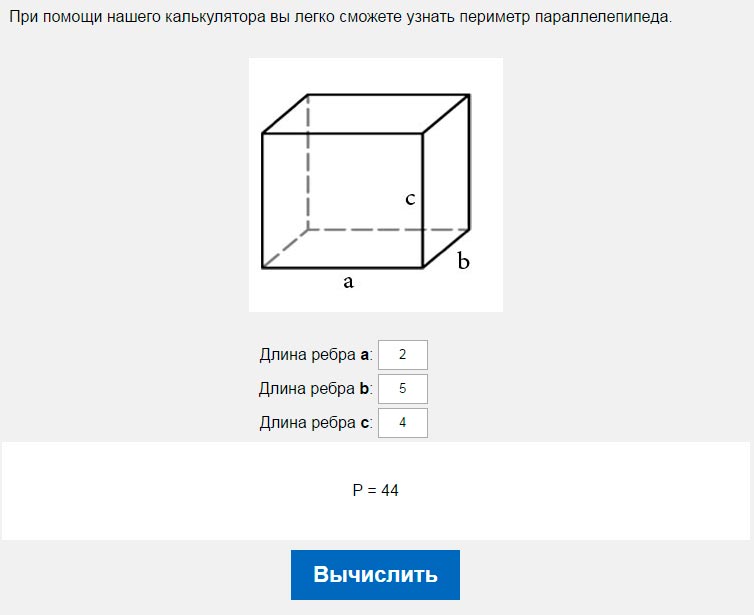
Найдем производную .
, отсюда и — критические точки.
Найдем интервалы знакопостоянства производной и посмотрим является ли точка точкой минимума (см. рис.4).
Рис. 4. Интервалы знакопостоянства производной.
Таким образом, точка является точкой минимума. Напомним, мы должны найти такую точку, при которой периметр будет наименьшим. Выяснили, что на всем промежутке значение функции в точке является наименьшим, так как на промежутке функция убывает, а на промежутке – возрастает. Точка экстремума на промежутке — единственная.
Найдем . И, наконец, найдем .
Итак, требовалось найти такой параллелепипед, у которого наименьший периметр боковой грани и вычислить этот периметр. Параллелепипед нашли, он имеет измерения . Наименьшее значение периметра боковой грани равно .
3.

Итак, мы рассмотрели стереометрические задачи на экстремум, которые решаются с помощью производной. Решили две взаимно обратные задачи на прямоугольный параллелепипед с использованием формул и боковых сторон параллелепипеда. В первой задаче нужно было найти максимальное значение объема, а во второй – наименьшее значение периметра в прямоугольном параллелепипеде. Эти задачи, как и в планиметрии, решаются следующим образом: составляется нужная функция, она оказывается функцией двух переменных, выписываются геометрические связи, они позволяют выразить одну переменную через другую и получить функцию только от одной переменной. Дальше применяя производную, можно успешно решить задачу.
Список рекомендованной литературы по теме «Прямоугольный параллелепипед формулы», «Боковые стороны параллелепипеда»
1. Алгебра и начала анализа, 10 класс (в двух частях).
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics.ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал Exponenta.ru (Источник).
Сделай дома — решение задач на прямоугольный параллелепипед, как найти сторону прямоугольного параллелепипеда
№ 46.59, 46.50 (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
Как найти площадь поверхности прямоугольного параллелепипеда: формула
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Изучите концепцию, формулу, сравнение, примеры
0
Сохранить
Скачать публикацию в формате PDF
Периметр куба равен 12а в единицах.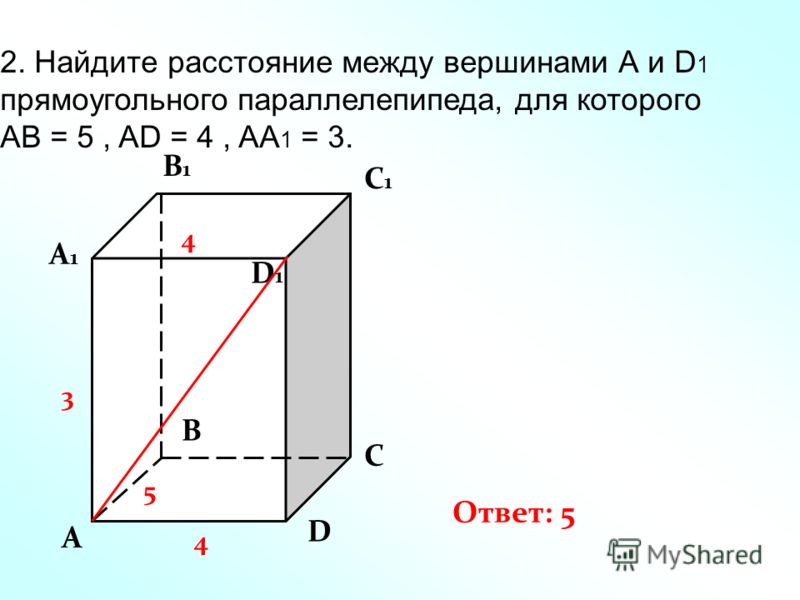
Периметр куба
Можно считать, что куб состоит из двумерных фигур, поскольку каждая из его шести граней представляет собой квадрат. У него восемь вершин, шесть граней и двенадцать ребер. Эти двенадцать ребер всегда параллельны каждому из его противоположных ребер. Следовательно, периметр куба должен быть равен общей сумме его ребер или длин.
Рассмотрим рисунок выше,
Каждая сторона равна «a» единицам, всего 12 сторон,
Следовательно, периметр куба (P) = 12 x a = 12 a.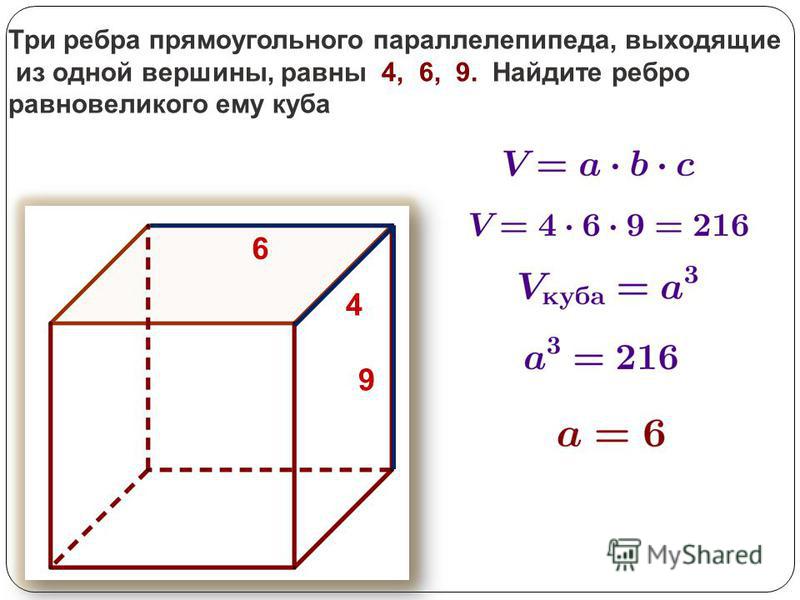
Периметр куба Формула
Формула для Периметра куба дается следующим образом:
Периметр куба (P) = 12 x a (единиц).
Где a = длина каждой стороны куба.
Периметр куба и площадь поверхности куба
Давайте кратко обсудим площадь поверхности куба и чем она отличается от периметра.
| Периметр куба | Площадь поверхности куба |
| Периметр – это сумма длин всех сторон куба, умноженная на 12. | Принимая во внимание, что площадь поверхности куба равна сумме площадей всех его граней. |
| Мы знаем, что куб имеет 6 граней в форме квадрата. Следовательно, площадь поверхности куба = 6 x площадь поверхности квадратной грани = 6 x a². | Площадь поверхности квадрата равна квадрату его длины, определяемой по формуле Площадь поверхности квадрата = a², где «a» — длина каждой из его сторон. |
| Периметр куба равен сумме длин каждой из его сторон | Площадь поверхности равна сумме площадей каждой из его граней. |
Периметр решенного куба Примеры
Пример 1 . Длина ребер в кубе равна 8,5 см каждое. Каков будет периметр куба?
Решение 1.
Приведены данные,
Длина каждого ребра в кубе = 8,5см.
Формула Периметр куба = 12 x a.
= 12 х 8,5 см.
= 102 см.
Периметр куба равен 102 см.
Пример 2 . Площадь поверхности куба 64 м², какой длины будет его ребро?
Решение 2.
Приведены данные,
Площадь поверхности куба = 64 м²
Формула площади поверхности куба = 6 х а², где а — длина каждой из его сторон.
64 = 6 x а²
а² = 64 / 6
а² = 10,66
а = 3,26 см.
Длина каждой стороны куба равна 3,26 см.
Пример 3 . Найдите периметр и площадь поверхности куба, если длина каждой из его сторон равна 5 см.
Решение 3,
Приведенные данные,
Длина каждой стороны куба (а) = 5 см
Периметр куба = 12 х а = 12 х 5 = 60 см.
Площадь поверхности куба = 6 x a² = 6 x 25
= 150 см².
Следовательно, периметр данного куба равен 60 см, а площадь его поверхности 150 см².
Надеюсь, эта статья была информативной и помогла вам в учебе и подготовке к экзаменам. Оставайтесь с нами в приложении Testbook, чтобы узнать больше об обновлениях и темах, связанных с математикой и другими подобными предметами. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний о связанных экзаменах.
Часто задаваемые вопросы о периметре куба
В.1 Как преобразовать периметр куба в сторону?
Ответ 1 Периметр куба определяется по формуле Периметр (P) = 12 x a, где «a» — длина каждой стороны. Следовательно, применяя формулу для данного периметра куба, мы можем вычислить длину его стороны.
Q.2 Чему равен периметр прямоугольного параллелепипеда?
Ответ 2 Периметр прямоугольного параллелепипеда определяется по формуле 4 x (L+B+H), где L = длина куба, B = ширина куба и H = высота куба.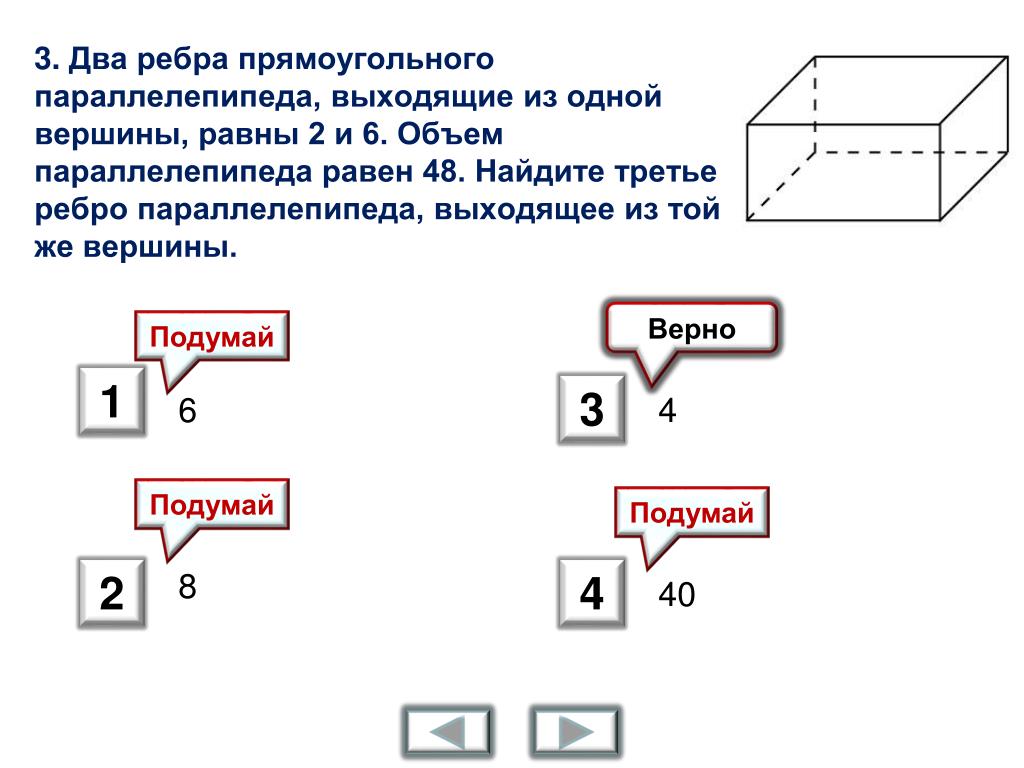
Q.3 Каков периметр одной грани куба?
Ответ 3 Одна грань куба в основном представляет собой квадрат, а квадрат имеет четыре ребра, следовательно, периметр одной грани куба равен 4 x a, где «a» — длина стороны.
Q.4 Как найти основание куба?
Ответ 4 Основание куба — квадрат, поэтому его площадь основания будет равна а², где «а» — длина каждой стороны.
Q.5 Как найти периметр куба?
Ответ 5 Периметр куба определяется по формуле Периметр (P) = 12 x a, где «a» — длина каждой стороны.
Скачать публикацию в формате PDF
Еще на testbook.com
| Равномерное распределение в вероятности: типы, формулы и примеры |
| Периметр равнобедренного треугольника: изучите понятие, родственную формулу и решенные примеры. |
| Обратная связь: изучите определение, теорему, область определения и диапазон на примерах! |
Сумма N терминов в AP: изучите концепцию, доказательства и решенные примеры. |
| Однородное дифференциальное уравнение: изучите типы определений на примерах |
Функция — Как вычислить периметр прямоугольного параллелепипеда?
Шаги этой задачи относительно просты.
- Получить длину, ширину и ширину.
- Убедитесь, что значения находятся в требуемых пределах.
- Вычислите периметр.
- Укажите расчетный периметр или длину, в зависимости от того, насколько педантичен человек, пишущий эти требования.
Номер четыре, вероятно, является самой сложной частью этой задачи, и вам следует связаться с человеком, составившим требования, чтобы убедиться, что вывод : возврат длины кубоида на самом деле является опечаткой и что вы должны вернуть периметр кубоида.
В этом примере я предполагаю, что это вопрос с подвохом, и укажу длину; однако, если это не вопрос с подвохом, а опечатка, вам следует заменить переменную длины (LE) на переменную периметра (PE) в строке вывода (80).
10 ЕСЛИ НЕТ (LE < 1 ИЛИ LE > 100 ИЛИ BR < 1 ИЛИ BR > 100 ИЛИ WI < 1 ИЛИ WI > 100), ТО 60 20 ВВОД "ДЛИНА, ШИРИНА, ШИРИНА"; LE, BR, WI 30 ЕСЛИ LE < 1 ИЛИ BR < 1 ИЛИ WI < 1, ТОГДА НАПЕЧАТАЙТЕ «ВЫ ВВЕЛИ»: НАПЕЧАТАЙТЕ «MICROVERSE. ПОЖАЛУЙСТА, УБЕДИТЕСЬ, ЧТО»: 40 ЕСЛИ LE > 100 ИЛИ BR > 100 ИЛИ WI > 100, ТОГДА ВЫБЕРИТЕ ГРАНИЦЫ: ВЫШИТЕ "ИЗВЕСТНУЮ ВСЕЛЕННУЮ". " 50 ПЕРЕЙТИ К 10 60 PE = ЛЭ + БР + ВИ 70 ПЭ=ПЭ*4 80 PRINT "ДЛИНА КУБОИДА:";LE 90 КОНЕЦ
Бейсик никогда не был известен своей удобочитаемостью, и даже эта короткая программа, вероятно, трудна для понимания. Вот та же программа в более читабельной форме:
цикл while (%length% < 1 или %length% > 100 или %breadth% < 1 или %breadth% > 100 или %width% < 1 или %width% > 100)
ввод "Длина, Ширина, Ширина"; %длина%, %ширина%, %ширина%
выключатель
case (%length% < 1 или %breadth% < 1 или %width% < 1)
Wrap Вы вошли в микровселенную. Пожалуйста, убедитесь, что все размеры составляют не менее 1 единицы. case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%
case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%
Здесь используется SuperBASIC не в качестве рекомендации (если, что маловероятно, BASIC, который вы используете, не находится на цветном компьютере TRS-80), а просто потому, что я знаком с этим препроцессором BASIC. Эти две программы в чем-то эквивалентны в том смысле, что я написал более читаемый код, а затем использовал скрипт для перевода его на BASIC.
Вы можете увидеть шаги, описанные выше: введите размеры прямоугольного параллелепипеда; убедиться, что размеры находятся в требуемых пределах; и либо зациклить
обратно на запрос ввода , если они не равны, или вычислить периметр и напечатать длину, если они есть.
Как найти периметр куба
Строго говоря, такого понятия как периметр куба, в математике не существует. Однако по аналогии с площадью поверхности куба, равной суммарной площади всех граней, можно ввести и понятие периметра куба. Наиболее логичным определением этого термина будет «сумма длин всех ребер куба». Эта величина может пригодиться, например, при изготовлении каркаса куба.

Вам понадобится
- — куб;
- — линейка.
Инструкция
Чтобы найти периметр куба, определите длину одного из его ребер и умножьте это число на 12. В виде формулы это правило можно записать следующим образом:P = 12 * a,где:Р – периметр куба,а – длина его стороны.Подобная формула может понадобиться если нужно собрать каркас куба, равного существующему.
Пример: учитель решил изготовить наглядное пособие «кубометр» — каркас куба с длиной ребра 1 метр.Вопрос: сколько метров трубы понадобится для изготовления модели куба?Решение: 1 (м) * 12 = 12 метров.
Если нужно рассчитать размер куба, каркас которого можно сделать из имеющегося материала (проволоки, арматуры, трубы, уголка и т.п.), разделите эту длину на 12. Или, в виде формулы:а = Р / 12
Пример: имеется отрезок проволоки длиной 1 м 20 см.Требуется: определить максимальный размер каркаса куба, который можно согнуть из этой проволоки.Решение:1 м 20 см = 120 см. (переводим значение длины в одну систему измерения).120 см / 12 = 10 см. (находим максимальную длину ребра куба).
Если известен объем куба, то для нахождения его периметра умножьте на 12 корень кубический из его объема.P = 12 * √³V,где: V – объем куба,√³ — обозначение кубического корня.
Пример: сколько метров уголка понадобится для изготовления кубического аквариума объемом 27 литров?Решение: переведите литры в кубические метры: 27/1000=0,027м³.Найдите из 0,027 кубический корень (это будет длина одного ребра): √³0,027=0,3 (м).Умножьте длину ребра на 12: 0,3 * 12 = 3,6 (метров).
Если задана площадь поверхности куба, то чтобы найти его периметр, воспользуйтесь следующими соотношениями:S = 6 * а²,Р = 12 * а,где: S – площадь поверхности куба,откуда:Р = 12 * √(S/6) = 2 * 6 * √S / √6 = 2 * √S * √6 * √6 / √6 = 2 * √S * √6 = 2√6√S, то есть:.Р = 2√6√S
Пример: на дачном участке установили емкость для воды, имеющую форму куба. На ее изготовление ушло 25 квадратных метра листового железа. Чтобы бак для воды стал более прочным его решили обварить металлическим уголком.Вопрос: сколько уголка понадобится?Решение: воспользуйтесь выше выведенной формулой:Р = 2√6√25 ≈ 24,5 (метра).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.





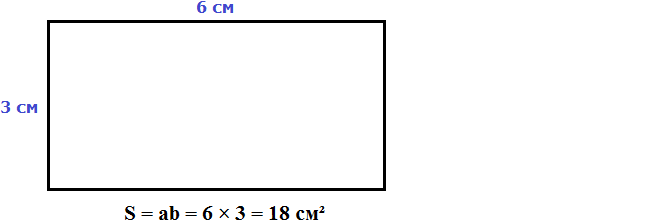
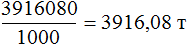


 case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%
case (%length% > 100 или %breadth% > 100 или %width% > 100)
wrap Вы покинули пределы известной вселенной. Пожалуйста, убедитесь, что все размеры не превышают 100 единиц.
концевой выключатель
концевая петля
%периметр% = %длина% + %ширина% + %ширина%
%периметр% *= 4
print "Длина прямоугольного параллелепипеда:";%length%