|
Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам: Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим Ксарфакс 4 года назад Периметр по координатам Периметр фигуры — это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2): Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой:
Sadness 4 года назад Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так:l=sqrt((x2 — x1)^2 + (y2 — y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере:Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((12 — 1)^2 + ((-5) — 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((-2 — 12)^2 + (1 — -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 — (-2))^2 + (8 — 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты. Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым — просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула: , где х1 и х2 — координаты концов отрезка по оси х, а y1 и y2 — координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины. Hamster1337 2 года назад Периметр геометрических фигур по координатам вершин можно найти при помощи формулы Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр. Алиса в Стране 3 года назад Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр — сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула: где точка А имеет координаты (x1; y1), а точка В — координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС. габбас 4 года назад Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 — x1^2) + (y2^2 — y1^2), х1 и у1 координаты начала, х2,у2 — координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюминка 3 года назад Во-первых, вспомним, что такое периметр — это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb — xa)2 + (yb — ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2): Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить — получить. Бекки Шарп 3 года назад Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле: У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле. Складываем полученные результаты и получаем периметр. Бархатные лапки 3 года назад Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр. Знаете ответ? |

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
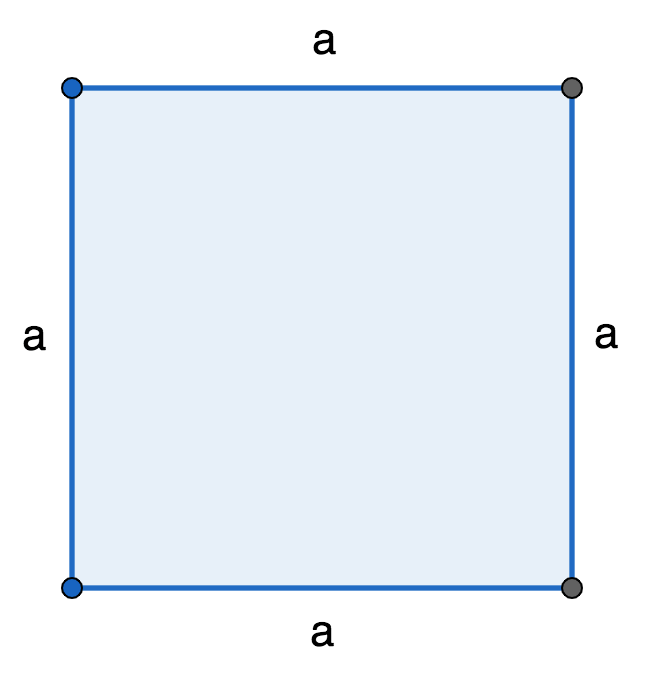
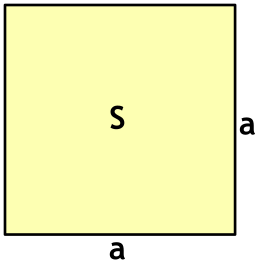
Квадрат — четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a — сторона квадрата
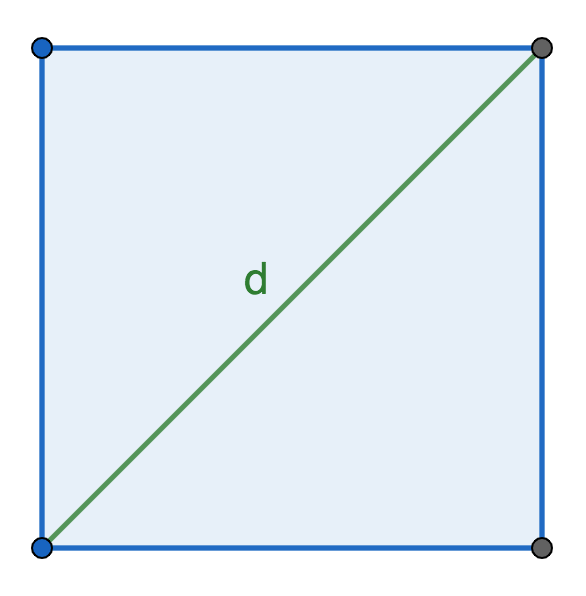
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d — диагональ квадрата
Формула периметра квадрата через площадь
{P = 4sqrt{S}}
S — площадь квадрата
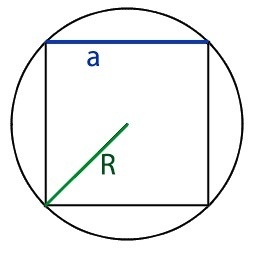
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R — радиус описанной около квадрата окружности
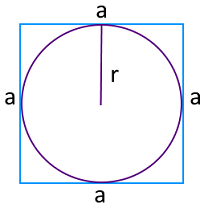
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r — радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем — 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде — 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор — 2 * sqrt(2).
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
-
Формула вычисления периметра
- По длине стороны
- По длине диагонали
- Примеры задач
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:
P = d ⋅ 2√2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
Содержание
- Как найти периметр квадрата
- Основные определения
- Формула нахождения периметра квадрата
- Если известна длина стороны
- Если известна длина диагонали
- Решение задач
- 1. Найти периметр квадрата, диагональ которого равняется √4 см.
- 2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах
- 3. Периметр квадрата 48 см. Чему равна его сторона?
- 4. Периметр квадрата 20 см. Как найти его площадь?
- Как найти периметр фигуры
- Определение периметра
- Формула нахождения периметра
- Треугольник
- Квадрат и ромб
- Прямоугольник и параллелограмм
- Равнобедренная трапеция
- Решение задач
- Нахождение периметра квадрата: формула и задачи
- Формула вычисления периметра
- По длине стороны
- По длине диагонали
- Примеры задач
- Периметр квадрата
- О периметре квадрата.
- Формула периметра квадрата
- Что такое периметр квадрата
- Как найти периметр квадрата. если известна сторона!?
- Как найти периметр квадрата. если известна площадь!?
- Как найти периметр квадрата
- Что такое периметр квадрата
- Способы вычисления
- По длине стороны
- По длине диагонали
- По площади
- По радиусу описанной окружности
- По радиусу вписанной окружности
Как найти периметр квадрата
О чем эта статья:
2 класс, 3 класс
Основные определения
Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.
Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула нахождения периметра квадрата
Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят 2 и 3 класс.
Если известна длина стороны
P = a + a + a + a, где a — сторона.
Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 * a
Если известна длина диагонали
P = d * 2 * √2, где d — диагональ.
Диагональ — это отрезок, который соединяет противоположные стороны фигуры.
Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров, как можно чаще. Давайте сделаем это прямо сейчас!
Занимайся изучением математики онлайн! Курсы по математике для учеников с 1 по 11 классы!
Решение задач
1. Найти периметр квадрата, диагональ которого равняется √4 см.
- Воспользуемся формулой P = d * 2 * √2;
- P = √4 * 2 * √2;
2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах
- Воспользуемся формулой P = 4 * a;
- P = 4 * 97
3. Периметр квадрата 48 см. Чему равна его сторона?
- Воспользуемся формулой P = 4 * a;
- Значит a = P : 4;
- a = 48 : 4;
4. Периметр квадрата 20 см. Как найти его площадь?
- Воспользуемся формулой P = 4 * a;
- Тогда a = P : 4;
- a = 20 : 4 = 5 см;
- Воспользуемся формулой S = a * a;
- Значит S = 5 * 5;
Источник
Как найти периметр фигуры
О чем эта статья:
Определение периметра
Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Формула нахождения периметра
Рассмотрим пять фигур.
Треугольник
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.
P = 3 * a, где a — длина стороны.
Квадрат и ромб
Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично.
P = 4 * a, где a — длина стороны.
Прямоугольник и параллелограмм
Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно.
P = 2 * (a + b), где a — ширина, b — высота.
Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы!
Равнобедренная трапеция
Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.
P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 * (a + b), нам нужно найти ширину;
- Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные переменные в формулу: (10 +
* 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны 17см.
Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга.
- Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π;
- Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14;
Источник
Нахождение периметра квадрата: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√ 2 :
P = d ⋅ 2√ 2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√ 2 .
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √ 2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √ 2 см ⋅ 2√ 2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √ 2 = √ 2 см / √ 2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
Источник
Периметр квадрата
Периметр квадрата? как найти периметр квадрата, примеры, формула периметра квадрата.
О периметре квадрата.
Формула периметра квадрата
Интересный поисковый запрос — «что такое периметр квадрата«.
Что такое периметр квадрата
Слово периметр пришло из древности и например древние-греческом обозначала окружность(περίμετρον).
Или если совсем по простому — периметр квадрата это — сумма всех границ.
Периметр квадрата это сумма всех сторон квадрата, поскольку их 4 одинаковых, то одну сторону, надо умножить на 4.
Формула периметра квадрата — периметр квадрата равен стороне умноженной на 4 -> P=4a
Где P — периметр квадрата,
a — длина одной из сторон.
Как найти периметр квадрата. если известна сторона!?
Как мы уже говорили выше у нас есть формула нахождения периметра :
найдите периметр квадрата, если сторона квадрата равна 12 см.
Сторона квадрата это а, она равна 12см.
Подставляем 12 в формулу вместо буквы «а».
P = 4a -> P = 4 * 12-> P = 48см.
Если сторона квадрата равна 12 см, то периметр квадрата равен 48см.
Как найти периметр квадрата. если известна площадь!?
найдите периметр квадрата, если площадь квадрата равна 25см².
Опять вспоминаем формулу площади квадрата :
Из этой формулы нам требуется вывести сторону :
Далее берем формулу периметра квадрата и заменяем сторону на корень квадратный.
Извлекаем корень из 25 на калькуляторе
После этого умножаем на 4 :
Если площадь квадрата 25см², то периметр будет равен 20см.
Источник
Как найти периметр квадрата
Что такое периметр квадрата
Квадрат — это правильный четырехугольник, все его стороны и углы равны.
Про него также говорят, что это частный случай прямоугольника или ромба.
Периметр квадрата — это сумма длин всех его сторон или произведение одной его стороны на 4.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы вычисления
Для вычисления периметра квадрата применяется несколько видов несложных формул.
По длине стороны
Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:
где (a) — это сторона фигуры.
По длине диагонали
Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:
что следует из соотношения длин стороны и диагонали (d=asqrt2)
По площади
Зная площадь фигуры, найти ее периметр можно так:
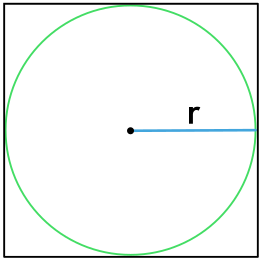
По радиусу описанной окружности
Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:
где R — радиус данной окружности.
По радиусу вписанной окружности
Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:
где r — радиус вписанной окружности.
Найти P квадрата, если его ребро a равно 5 см.
Так как P = 4a, подставляем сюда известное значение, и получается (P = 4times5= 20 см.)
Узнать P правильного четырехугольника, если его диагональ d равна 6 см.
Используем формулу (P;=;2dsqrt2) и подставляем известное значение. Получается: (P = 2 * 6sqrt2 = 12sqrt2 см.)
Ответ: (12sqrt2 см.)
Площадь квадрата равна 16 см². Каков периметр?
Мы знаем, что (P;=;4sqrt S\) . Значит, подставляя значение в формулу (P;=;4sqrt S\) , мы имеем: (P;=;4sqrt 16 = 4times4 = 16) см.
Известно, что 1/2 диагонали правильного прямоугольника составляет (9sqrt2\ ) см. Вычислить P.
1/2 диагонали имеющейся фигуры — это как раз радиус описанной окружности. Подставляем значение в уравнение (P;=;4Rsqrt2\) . Получается: (P;=;4Rsqrt2 = 4times9sqrt2timessqrt2 = 72) см.
Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.
Так как половина стороны данной фигуры — это радиус вписанной в нее окружности. Используем метод нахождения по радиусу вписанной окружности: (P;=;8r\) . Подставляем известное значение: (P;=;8r = 8times7 = 56 см.)
Источник
Perimeter of square is defined as the total length of the boundaries of that square. The perimeter of any shape can be obtained in the same pattern, that is, finding the total length of the shape’s boundary. A square is a closed regular polygon where all sides are equal, and all angles are 90° each. Square is a special type of quadrilateral as all four sides, angles, and diagonals are equal, also diagonals bisect each other at a right angle. Since all the sides of the square are equal, the perimeter of the square can be obtained by adding all the sides or by multiplying one side by 4.
What is Perimeter of Square?
The perimeter of any closed geometrical shape is obtained by finding the total length of the boundaries of its shape. Perimeter is the length that outlines the shape of the 2-D figures. The 2D figures include squares, rectangles, triangles, circles, and other polygons. For 2-D shapes, perimeter, and area is considered general calculations, and for 3-D shapes and forms surface area and volume is considered general calculation. The perimeter can be found for irregular shapes as well. Some of the commonly used terms with respect to 2-D shapes are as follows:
- Vertices: They are the endpoints of a shape.
- Edge/Side: A line segment joining two adjacent vertices.
- Diagonals: A line segment joining two nonadjacent vertices.
- Area: Area is the space occupied by a figure.
- Perimeter: The perimeter is the total length of the boundary of the figure.
- Angles: The point where two sides meet is the angle often measured in degrees or radians.
Perimeter of Square Formula
The perimeter of the Square can be calculated using the side length of the square. If the side of the square is represented as “a”, the formula for perimeter of square can be expressed as,
As shown above, the perimeter of a square is 4 times the length of its sides as all sides are equal in a square. The unit for the perimeter of a square is the unit used for length. It is measured in meters (m), centimeters (cm), inches (in), etc.
Example: Calculate the perimeter of a square having a side of 8cm.
Solution:
Perimeter of square = 4 × side
⇒ P = 4 × 8
⇒ P = 32 cm.
Derivation of Perimeter of Square
In order to find the perimeter of closed geometrical shape, the length of all the boundaries should be added. Similarly, to derive the perimeter of the square, we are required to add all the sides of the square, assume the length of the sides is denoted as “a”,
Perimeter = a + a + a + a
⇒ Perimeter of square = 4a
Where a is the side of the square.
How to Find the Perimeter of a Square?
Perimeter is the length of the boundary. It is often known as the distance around a closed 2D figure. The perimeters can be different according to the shapes given. The perimeter of a square can be calculated using side length, and there are cases when the side length is not given, then the perimeter of square can be obtained using diagonal and area. Therefore, the perimeter of square can be calculated using three methods,
- Using side length
- Using diagonal
- Using area
Perimeter of Square using Side Length
The below-given steps can be used to find the perimeter of square using side length,
- Measure the side of the square.
- Multiply the side length by 4.
- Express the perimeter obtained in the respective unit.
Perimeter of Square using Diagonal
However, if the side of the square is not given, but the diagonal is given, then the formula becomes,
Therefore, the Perimeter of square is,
The below-given steps can be used to find the area of the perimeter of the square using diagonals,
- Measure the diagonal of the square.
- Calculate the perimeter of the square using the formula, P = 4 × (Diagonal/√2).
Example: Find the perimeter of the diagonal is 4√2 m.
Solution:
The Perimeter of square is,
P = 4 × (Diagonal/√2)
⇒ P = 4 × (4√2/√2)
⇒ P = 16 m
Perimeter of Square using Area
When the area of square is given, let us assume the area of square is a. As we all know, Area = (side)2
Therefore, the perimeter of the square is,
The below-given steps can be used to find the area of the perimeter of square using area,
- Measure the area of the square.
- Calculate the area of the square using the formula, Perimeter = 4 × √Area.
Example: Find the perimeter if the area of the square is 49 square units.
Solution:
The Perimeter of square is,
P = 4 × √Area
⇒ P = 4 × √49
⇒ P = 28 units
Solved Examples on Perimeter of Square
Example 1: Find the perimeter of the square if the side given is 4 units.
Solution:
The Perimeter of square is,
P = 4 × side
⇒ P = 4 × 4
⇒ P = 16 units
Example 2: Find the side and perimeter of the square if the diagonal given is 2√2 cm.
Solution:
Side = Diagonal/√2
⇒ Side = 2√2/√2
⇒ Side = 2 cm
Perimeter of square = 4×side
⇒ Perimeter = 8 cm
Example 3: Find the side of the perimeter of the given square is √2.
Solution:
Perimeter = side × 4
⇒ √2 = side × 4
Therefore, Side = √2/4
Example 4: Find the diagonal if the perimeter of the square is 3√2 cm.
Solution:
Perimeter = 4 × (diagonal/√2)
⇒ (3√2 × √2 ) /4 = diagonal
⇒ Diagonal = 1.5 cm
Example 5: Find the perimeter if the area given is 25 sq units.
Solution:
Perimeter = 4√Area
⇒ Perimeter = 4√25
⇒ Perimeter = 20 units
Example 6: Find the area and perimeter of the square if its side is 3 units.
Solution:
Perimeter = 4×side
⇒ Perimeter = 4 × 3
⇒ Perimeter = 12 units
Area = (Side)²
⇒ Area = (3)²
⇒ Area = 9 sq units
FAQs on Perimeter of Square
Question 1: What is the perimeter of the square formula?
Answer:
The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,
P = 4 × Side.
Question 2: What is the unit of the perimeter of square?
Answer:
The units used for perimeter of square is the units used for length. The units used are meter (m), centimeter (cm), inches (in), etc.
Question 3: What is the area and perimeter of square?
Answer:
The perimeter of square is defined as the total length of its boundaries. The formula for perimeter of square is,
P = 4 × Side.
The space covered in 2-dimensional space by the square is called as area of a square. The formula used for area of square is,
A = Side2
Question 4: How to find the side length of the square when perimeter is given?
Answer:
In order to find the side length of square, first note down the formula for perimeter of square.
P = 4 × Side
Side = P/4
Hence, to find side length of square when perimeter is given, divide the perimeter by 4.
Read More
- Perimeter of Rectangle
- Perimeter of Triangle
- Circumference of a Circle





















 * 2 = 36 см;
* 2 = 36 см;