Расчёт периметра квадрата по диагонали
Периметр квадрата равен произведению длины его стороны на четыре или сумме длин четырёх его сторон.
Квадрат это четырёхугольник с прямыми углами и равными сторонами.
Калькулятор рассчитывает периметр квадрата по диагонали.
Для рассчёта нужно по теореме пифагора вычислить сторону квадрата, потом вычислить периметр.
По теореме пифагора находим длину стороны квадрата
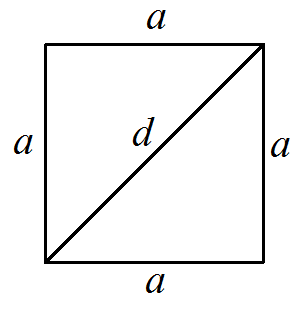
color{#0000FF}{d^{2} = a^{2} + a^{2}}
color{#0000FF}{d^{2} = 2 times a^{2}}
color{#0000FF}{a = sqrt{frac{ d^2 }{ 2 }}}
Находим периметр квадрата
color{#0000FF}{P = a times 4}
Значащих цифр:
Похожие калькуляторы

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат — четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a — сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d — диагональ квадрата
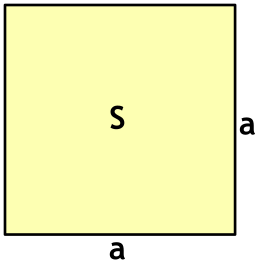
Формула периметра квадрата через площадь
{P = 4sqrt{S}}
S — площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R — радиус описанной около квадрата окружности
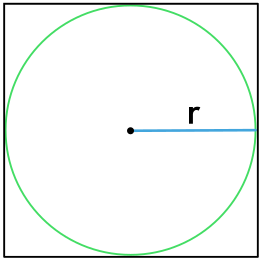
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r — радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем — 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде — 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор — 2 * sqrt(2).
Калькулятор периметра квадрата через его диагональ
При помощи данного калькулятора можно вычислить периметр квадрата зная его диагональ.
Диагональ квадрата d
Для того что бы вычислить периметр квадрата зная длину его диагонали нам необходимо первым действием вычислить длину его стороны воспользовавшись следующей формулой:
a = d/√2
Когда мы узнали длину стороны квадрата нам необходимо полученный результат умножить на 4, из чего следует, что формула периметра квадрата, вычисляемая через его диагональ, выглядит следующим образом:
P = 4d/√2
или
P = 2d√2
Где:
d — диагональ квадрата.
P — периметр квадрата.
a — сторона квадрата
Приимер решения
d = 46
Для того, чтобы вычислить периметр квадрата зная длину его диагонали, нам необходимо воспользовавшись теоремой Пифагора, узнать длину его стороны.
a = d/√2 = 46/1.41421356 = 32.52691
Таким образом, мы узнали длину стороны квадрата которая равна 32.52691
Теперь для того, чтобы узнать периметр данного квадрата, нам необходимо длину всех его 4 сторон сложить между собой, а так как все стороны квадрата равны между собой, нам можно просто длину стороны квадрата умножить на 4.
P = 32.52691*4 = 130.1076
В случае если мы хотим данную задачу решить в одно действие нам надо воспользоваться следующей формулой
P = 2d√2
Подставляем в данную формулу нужное нам значение:
P = 2*46√2 = 130.1076
Распишем подробнее:
P = 2*46√2 = 92*1.41421356 = 130.1076
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
-
Формула вычисления периметра
- По длине стороны
- По длине диагонали
- Примеры задач
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a
Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:
P = d ⋅ 2√2
Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
Квадрат это четырехугольник, у которого все стороны равны и углы между сторонами тоже равны. Все углы квадрата прямые. Найти периметр квадрата можно несколькими способами, все зависит от того, какие исходные данные известны.
.
Найти периметр квадрата зная его сторону
Формула для нахождения периметра квадрата через сторону: , где a — сторона квадрата
Найти периметр квадрата зная его диагональ
Формула для нахождения периметра квадрата через диагональ: P=2d√2 где d- диагональ квадрата.
Найти периметр квадрата зная его площадь
Формула для нахождения периметра квадрата через площадь: P=4√S , где s- площадь квадрата.
Найти периметр квадрата через радиус описанной окружности
Формула для нахождения периметра квадрата через радиус описанной окружности: P=4R√2 , где R- радиус описанной окружности.
Найти периметр квадрата через радиус вписанной окружности
Формула для нахождения периметра квадрата через радиус вписанной окружности: P=8R , где R- радиус вписанной окружности.
Радиус вписанной окружности