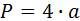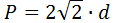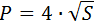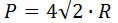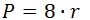Как найти периметр квадрата, если известна его площадь
Квадрат представляет собой правильный четырехугольник (или ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у любого иного правильного многоугольника, у квадрата можно высчитать периметр и площадь. Если площадь квадрата уже известна, то найти его стороны, а затем и периметр не составит труда.

Инструкция
Площадь квадрата находится по формуле:
S = a²
Это означает, что для того, чтобы вычислить площадь квадрата, нужно умножить длины двух его сторон друг на друга. Как следствие, если знать площадь квадрата, то при извлечении корня из данного значения можно узнать длину стороны квадрата.
Пример: площадь квадрата 36 см², чтобы узнать сторону данного квадрата, необходимо извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см
Для нахождения периметра квадрата необходимо сложить длины всех его сторон. С помощью формулы это можно выразить так:
P = a+a+a+a.
Если извлечь корень из значения площади квадрата, а затем сложить получившуюся величину 4 раза, то можно найти периметр квадрата.
Пример: Дан квадрат с площадью 49 см². Требуется найти его периметр.
Решение:
Сначала необходимо извлечь корень площади квадрата: √49 = 7 см
Затем, вычислив длину стороны квадрата, можно вычислить и периметр: 7+7+7+7 = 28 см
Ответ: периметр квадрата площадью 49 см² составляет 28 см
Обратите внимание
Для квадрата справедливы следующие определения:
Квадрат — это прямоугольник, который обладает равными между собой сторонами.
Квадрат — это особая разновидность ромба, у которого каждый из углов равен 90 градусам.
Являясь правильным четырехугольником, вокруг квадрата можно описать или вписать окружность. Радиус вписанной в квадрат окружность можно найти по формуле:
R = t/2, где t — сторона квадрата.
Если же окружность описана вокруг него, то ее радиус находится так:
R = (√2*t)/2
Исходя из данных формул, можно вывести новые для нахождения периметра квадрата:
P = 8*R, где R — радиус вписанной окружности;
P = 4*√2*R, где R — радиус описанной окружности.
Квадрат является уникальной геометрической фигурой, поскольку он абсолютно симметричен, независимо от того, как и где провести ось симметрии.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* — обязательно заполнить
Площадь (S) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{S}) = (sqrt{10}) = 3.16
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3.16^{2}}) = 4.47
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3.16}{2}) = 1.58
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.47}{2}) = 2.24
Периметр (P) = (L*4) = (3.16*4) = 12.64
Калькулятор периметра квадрата через его площадь
При помощи данного калькулятора можно вычислить периметр квадрата через его площадь.
Площадь квадрата S
Периметр квадрата:
Для того что бы вычислить периметр квадрата зная его площадь необходимо воспользоваться следующей формулой:
P = 4√S
Где:
S — площадь квадрата.
P — периметр квадрата.
Как найти периметр квадрата, если известна его площадь
Квадрат представляет собой правильный четырехугольник (или ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у любого иного правильного многоугольника, у квадрата можно высчитать периметр и площадь. Если площадь квадрата уже известна, то найти его стороны, а затем и периметр не составит труда.
Площадь находится по формуле:
S = a²
Это означает, что для того, чтобы вычислить площадь квадрата, нужно умножить длины двух его сторон друг на друга. Как следствие, если знать площадь квадрата, то при извлечении корня из данного значения можно узнать длину стороны квадрата.
Пример: площадь квадрата 36 см², чтобы узнать сторону данного квадрата, необходимо извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см
Для нахождения периметра квадрата необходимо сложить длины всех его сторон. С помощью формулы это можно выразить так:
P = a+a+a+a.
Если извлечь корень из значения площади квадрата, а затем сложить получившуюся величину 4 раза, то можно найти периметр квадрата.
Пример: Дан квадрат с площадью 49 см². Требуется найти его периметр.
Решение:
Сначала необходимо извлечь корень площади квадрата: √49 = 7 см
Затем, вычислив длину стороны квадрата, можно вычислить и периметр: 7+7+7+7 = 28 см
Ответ: периметр квадрата площадью 49 см² составляет 28 см
Периметр квадрата калькулятор онлайн умеет вычислять периметр пятью способами:
- По стороне квадрата.
- По диагонали квадрата.
- По площади квадрата.
- По радиусу описанной окружности.
- По радиусу вписанной окружности.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр квадрата — это сумма четырех его сторон.
Так как у квадрата все стороны равны, то для вычисления периметра достаточно знать длину всего одной стороны.
Периметр может быть найден и по другим формулам, например через диагональ или площадь квадрата. В этих случаях сначала находится длина одной стороны квадрата, а затем и сам периметр.
Как найти периметр квадрата?
Найти периметр квадрата очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По стороне
где а — сторона квадрата.
2) По диагонали
где d — диагональ квадрата.
3) По площади
где S — площадь квадрата.
4) По радиусу описанной окружности
где R — радиус описанной окружности.
5) По радиусу вписанной окружности
где r — радиус вписанной окружности.
Скачать все формулы в формате Word/PDF