Задания
Версия для печати и копирования в MS Word
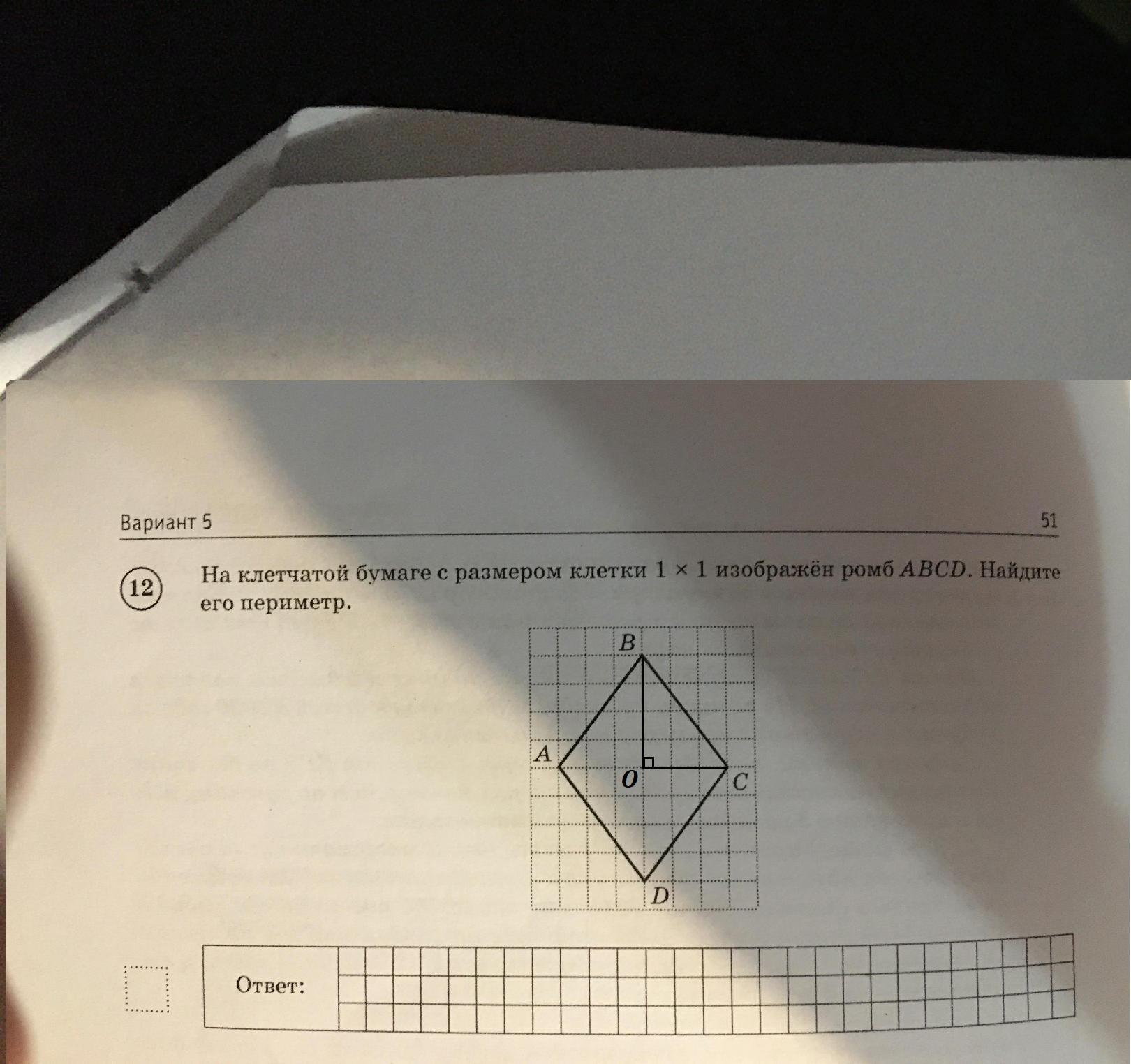
На клетчатой бумаге с размером клетки 1 × 1 изображён ромб ABCD. Найдите его периметр.
Спрятать решение
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из рисунка видно, что диагонали AC и BD равны 8 и 6 соответственно. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдём сторону ромба: Так как все стороны ромба равны, то периметр равен:
Ответ: 20.
Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки 
Средняя линия трапеции равна полусумме её оснований:
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

Получим:
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Как найти периметр четырехугольника на клетчатой бумаге 1х1
Условно проведем диагонали ромба ABCD, которые делятся точкой пересечения пополам и образуют между собой угол 90°
Тогда АО = 3 см и ВО = 4 см, а значит, из ΔАОВ по теореме Пифагора (или по правилу египетского треугольника):
АВ = √9+16 = √25 = 5 см
*По египетскому треугольнику если катеты равны 3 и 4 см, то гипотенуза равна 5 см*
Периметр ромба равен 4а , т.к. все его стороны равны
http://megamozg.com/task/11912162
Помогите и объясните как периметр и площадь находить по клеточкам
?
Вопрос задан Максим Сечов
1 октября 2019 в 1 — 4 классы.
0
Не отслеживать
Отмена
Добавить
1 Ответы
Площадь фигуры — это число целых клеточек в фигуре. 1 клетка = 1 см²
S = (3+2+3+2) = 10 см² — ОТВЕТ
Периметр — сумма длин всех его сторон. Например, по часовой стрелке.
Р = 3 + 3 +1 + 1 + 2 + 2 +1 + 1 + 1 + 1 = 16 см — ОТВЕТ
Ответ дан Ариана Ступанова
1 октября 2019.
0
Отмена
Добавить
Авторизуйтесь, чтобы ответить
Ответ:
20
Пошаговое объяснение:
- Ромб — параллелограмм, у которого все стороны равны.
⇒ AB = BC = CD = AD
Внутри данного ромба построим прямоугольный ΔBOC, где BC — гипотенуза.
Так как 1 клетка = 1 ⇒ OC = 3 (так как 3 клетки) и BO = 4 (так как 4 клетки)
В ΔBOC:
Найдём BC по теореме Пифагора:
⇒ AB = BC = CD = AD = 5
- Периметр фигуры — сумма всех её сторон.
⇒
Или:
Так как в ромбе все стороны равны и этих сторон всего 4, то:
Приложения:
6 декабря 2022 13:07
6943
Как найти периметр фигуры по клетками помогите пожалуйста
Посмотреть ответы
Ответ:
Р=4+4+2+2+2+2+1+1+1+1+1+1 Р=22
Ответ:
22 см
Пошаговое объяснение:
периметр — это сумма длин всех сторон. надо посчитать по клетками, сколько составляет длина каждой стороны и сложить все это.
4 + 2 + 1 + 1 + 1 + 2 + 4 + 2 + 1 + 1 + 1 + 2 = 22 см
Еще вопросы по категории Математика
Помогите решить пожалуйста: составь неравенства и проверь их: 1) частное чисел 7020 и 90 больше разности чисел 5030 и 4961 2) произведение чисел 704…
Чему равно количество грамм в 1 кг?…
Начертите отрезок длиной 10 см и разделите его штрихами 5 равных частей…
Какие примеры профессионализма могут быть в IT-сфере?…
Подчеркните значащие цифры числа: а)3,52 б)0,352 в)0,03520 г)7,405 д)4,203 е)0,005 ж)0,0420 з)7,0003 И)10,0050 К)6,700 л)0,00067 м)0,0100…

























