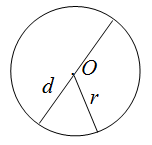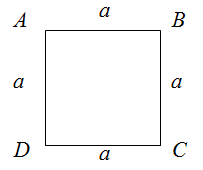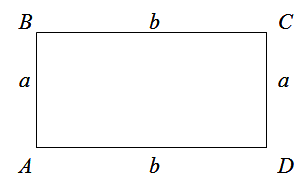In this platform, you have to learn about how to find the Perimeter and Area of irregular figures. An irregular shape will be of any size and length. We will see irregular shapes all around us, for example, a diamond shape, a kite, a leaf, a flower, etc. The Area of irregular shapes will be the space occupied by the shape which is measured in square units. The Perimeter of irregular shapes is by adding all the lengths of their sides. Any shape whose sides and angles are not of equal length is named an irregular shape.
On this page, you will learn about the definition of the area and the perimeter of irregular figures, how to find the area and perimeter of irregular figures, some solved example problems, and so on.
Read More:
- Area and Perimeter of Combined Figures
- Area of a Circular Ring
- Worksheet on Area of the Path
Irregular Figures – Definition
The Irregular Figures are defined as a figure that is not a standard geometric shape. An irregular shape is simply a shape where every single side is not the same length. But some irregular figures are made up of two or further standard geometric shapes. If the shape is irregular then it has some angles that are not all the same size. Based on the number of sides or corners we can decide that irregular figure.
How to find Perimeter and Area of Irregular Figures?
The following are the ways for finding the area and perimeter of irregular figures:
How to find Area of Irregular Shapes or Figures?
- Step 1: First, divide the compound shape into a basic regular shape.
- Step 2: Next, find each basic shape area separately.
- Step 3: Now Add all the areas of basic shapes together.
- Step 4: Now, write the final answer in square units.
How to find the Perimeter of Irregular Figures?
To find the perimeter of the irregular figure, we can simply add up each of its outer sides length of a shape. To find the perimeter of any shape like rectangle, square, and so on you have to add all the lengths of four sides. Consider ‘A’ is in this case the length of the rectangle and ‘B’ is the width of the rectangle.
See More:
- Plane Figures
- Solid Figures
- Rectilinear Figures
Perimeter and Area of Irregular Shapes Examples
Example 1:
The Irregular Figure is given below. Find the area of that figure?
Solution:
As given in the question, the irregular figure is given.
Now, we can break the given irregular figure. After separating the figure we have two rectangle blocks.
Next, we will find the area of those two rectangles. The area of the irregular figure is the sum of the areas of two rectangles.
The width of one block is 12 and the length of the block is 4.
Next, the width of the other rectangle is 2, but its length is not given. By using the upper rectangle length we can find the length of the lower rectangle. So the right side of the figure is the length of the upper rectangle block plus the length of the lower rectangle block.
Since the total length is 10 units, the right side of the upper rectangle is 4 units long. So the length of the lower rectangle will be 6 units.
So the area of the figure is,
The Area of the figure is the Area of the upper rectangle + Area of the lower rectangle
We know that the Area of the rectangle is, length x width (or) breadth.
So, the area of a figure is , lw + lw = 12(4) + 2(6).
Area of the figure is = 48 + 12 = 60sq.units.
Thus, the total area of the figure is 60 square units.
Example 2:
Find the area of the below-given irregular figure?
Solution:
As given in the question, the given figure is an irregular figure.
Now, we can break the given irregular figure. After separating the figure, we have two blocks one is a triangle block and another one is a rectangle.
Next, we will find the area of the irregular figure. The area of the irregular figure is the sum of the areas of two rectangles.
The rectangle has a length of 8 units and a width of 4 units. We need to find the base and height of the triangle.
On both sides of the rectangle 4units, the perpendicular side of the triangle is 3 units, which is 7- 4 = 3units.
Next, the length of the rectangle is 8units, so the base of the triangle is 3units, which is 8-5= 4units.
Now, we can add the areas then we get the area of the irregular figure.
So, the Area of the figure is the Area of the rectangle + the Area of the triangle.
We know the formulas, the area of the rectangle is, length x width (or) breadth.
The area of the triangle is 1/2bh.
So, the area of a figure is , lw + 1/2bh = 8(4) + 1/2(3)(3).
Area of the figure is = 32 + 4.5 = 36.5sq.units.
Hence, the total area of the given irregular figure is 36.5square units.
Example 3:
The figure is given below. Find the perimeter of the given Pentagon figure?
Solution:
As given in the question, the irregular shape figure is given.
This shape is a pentagon because it has five sides. Even though two of its sides are both 13m, it is an irregular pentagon because not all of its sides are the same length.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up the five side lengths.
We make the calculation easier by starting with the largest sides and also looking for number bonds to ten.
The two largest sides are 13m and 13m. These add together to make 26m.
The remaining three sides are 2m, 8m, and 9m. Now the value is 2m + 8m+ 9m = 19m.
Now, adding those two values are, 26m + 19m = 45m.
Thus, the perimeter of this given irregular pentagon is 45m.
Example 4:
Find the perimeter of the below-given figure?
Solution:
As given in the question, the figure is an irregular figure.
Now, we have to find the perimeter of the irregular figure.
To find the perimeter of this irregular shape, we add up all side lengths.
We make the mathematics easier by starting with the largest sides and also looking for number bonds to ten.
The largest sides is 10 cm. The remaining sides are 2cm, 2cm, 8cm, 8cm and 4 cm. Then the value is 2 cm + 2cm + 8 cm+ 8 cm + 4cm= 24cm.
Now, adding those two values are, 10 cm + 24 cm = 34 cm.
Thus, the perimeter of this given irregular figure is 34 cm.
FAQ’s on Perimeter and Area of Irregular Figures
1. What is meant by Irregular Figures?
An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or further standard geometric shapes.
2. Define Area of Irregular Figures?
The area of irregular shapes is defined as the quantity of space that is covered by an irregular shape. Irregular shapes are those shapes that do not have equal sides or equal angles. The unit for the area of an irregular shape is expressed in terms of square units, for representative, m2, cm2, in2, or feet2.
3. How to find the perimeter of Irregular Figures?
In order to calculate the perimeter of an irregular polygon we use the following two steps:
- Step 1: Note the length of each side of the given polygon.
- Step 2: Once the length of all the sides is acquired, then the perimeter is adding all the sides length.
Как посчитать периметр треугольника
Онлайн калькулятор
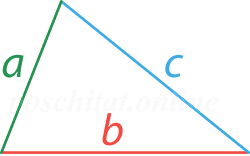
Периметр разностороннего треугольника
Чтобы вычислить чему равен периметр разностороннего треугольника вам нужно знать следующие параметры:
Введите их в соответствующие поля и узнаете чему равен периметр треугольника (Р).
Теория
Чему равен периметр разностороннего треугольника (P)?
Формула
Пример
К примеру, определим периметр разностороннего треугольника, у которого сторона a = 2 см, сторона b = 3 см, а сторона c = 4 см:
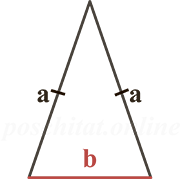
Периметр равнобедренного треугольника
Чтобы вычислить чему равен периметр равнобедренного треугольника вам нужно знать следующие параметры:
- длину двух равных сторон (a)
- длину основания (b)
Теория
Чему равен периметр равнобедренного треугольника (P)?
Формула
Пример
К примеру, определим периметр равнобедренного треугольника, у которого стороны a = 2 см, а сторона b = 3 см:
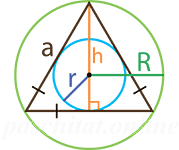
Периметр равностороннего треугольника
Чтобы вычислить чему равен периметр равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину трёх равных сторон (a)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
Как найти периметр треугольника
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как найти периметр треугольника
Вы будете перенаправлены на Автор24
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Точки в рамках определения 1 будем называть вершинами треугольника.
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Готовые работы на аналогичную тему
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2.
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
По определению периметра плоской геометрической фигуры, получим, что
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
По рассмотренному выше примеру, видим, что
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2cdot 12+11=35$ см
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2cdot 10+12=32$ см
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 07 2021
http://skysmart.ru/articles/mathematic/perimetr-treugolnika
http://spravochnick.ru/geometriya/podobnye_treugolniki/kak_nayti_perimetr_treugolnika/
Формула расчета периметра многоугольника
Содержание:
-
Что такое периметр многоугольника
- Свойства многоугольника
-
Как вычислить периметр правильного многоугольника
- Свойства правильного многоугольника
- Формула
-
Для неправильного многоугольника
- Описание
- Формула
-
По заданным координатам
- Как начертить многоугольник
- Формула для расчета периметра
- Примеры решения задач
Что такое периметр многоугольника
Определение
Периметр многоугольника в геометрии — это результат сложения длин всех его сторон.
Свойства многоугольника
- Все стороны прямые.
- Стороны не пересекаются (кроме звездчатых).
- Двумерная фигура.
- Сумма внешних углов всегда равна 360º.
- Сумма внутренних углов равна (frac{n(n-3)}2) (для правильных фигур).
Как вычислить периметр правильного многоугольника
Свойства правильного многоугольника
- Все стороны равны.
- Все углы равны.
- Центр равно удален ото всех вершин и сторон.
- Сумма всех углов равна 180º×(n−2).
- Все внешние углы при сложении их градусных мер дадут 360º.
- Все биссектрисы углов между сторонами равны и пересекают центр фигуры.
- Возможно вписать окружность и описать круг. Площадь кольца зависит от длины стороны многоугольника.
Формула
P=a×n
где a — длина стороны, n — количество сторон.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для неправильного многоугольника
Описание
У неправильного многоугольника все стороны разного размера.
Формула
Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.
P=a+b+c+d+…
Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.
Пример
Дан прямоугольник со сторонами 4см, 4см, 2см и 2см. Чтобы узнать периметр, можно просто их все сложить, как показано в формуле выше. А можно сделать так: 4×2+2×2, так как стороны попарно равны.
Этот способ подойдет и для фигур с большим количеством сторон, некоторые из которых равны.
Пример
Дан восьмиугольник со сторонами 5см, 5см, 3см, 3см, 3см, 2см и 1см. Периметр можно высчитать сложением, а можно считать так: 5×2+3×3+2+1.
По заданным координатам
Как начертить многоугольник
Еще один способ вычисления периметра многоугольника — построить фигуру на координатной прямой.
Для этого нужно:
- Построить координатные оси.
- Нанести на них заданные координаты (длины) сторон. Соединить точки.
Формула для расчета периметра
Далее нужно находить длины всех получившихся сторон.
- Размеры прямых сторон легко узнавать методом подсчета координатных меток между точками сторон. Записать получившиеся значения рядом со сторонами.
- Найти длину наклонных сторон. Это можно сделать по формуле: (d=sqrt{left(x_2-x_1right)^2+left(y_2-y_1right)^2})
Примечание
В формулу нужно подставить вместо x и y координаты сторон.
3. Найти периметр сложением длин всех сторон по формуле для неправильного многоугольника: P=a+b+c+d…, где a,b,c,d… — длины сторон. А если получился правильный: P=a×n, где a — длина стороны, а n — количество сторон фигуры.
Примеры решения задач
Примечание
Задания приведены разного уровня сложности. Расположены по принципу «от простого к сложному».
Во всех задачах нужно найти периметр фигур. Этот вопрос дублироваться в каждом примере ниже не будет.
Пример 1
Дан треугольник ABC. AB=28см, BC=51см, AC=46см.
Решение
P=AB+BC+AC=28+51+46=125см
Пример 2
В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.
Решение
AD=BC=12см
AB=CD=18см.
P=12×2+18×2=24+36=60см.
Пример 3
Дан квадрат со стороной 12 см.
Решение
Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.
Пример 4
Дана фигура (данные на рисунке).
Решение
На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.
Насколько полезной была для вас статья?
Рейтинг: 2.20 (Голосов: 5)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Содержание:
- Определения
- Формулы периметра основных геометрических фигур
Определения
Определение
Периметр — общая длина границы фигуры, которая чаще всего находится на плоскости.
Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры.
То есть периметр — это сумма длин сторон какой-либо геометрической фигуры.
Определение
Полупериметр — половина периметра. Употребляется в основном в геометрии треугольника.
Формулы периметра основных геометрических фигур
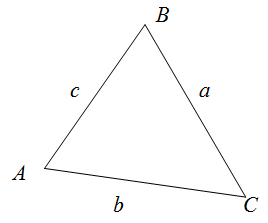
Периметр треугольника
Чтобы найти периметр треугольника $ABC$,
необходимо сложить длины всех его сторон.
$$P_{Delta A B C}=a+b+c$$
Читать дальше: формула периметра треугольника и примеры решений →
Периметр круга
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
Читать дальше: формула периметра круга и примеры решений →
Периметр квадрата
Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Читать дальше: формула периметра квадрата и примеры решений →
Периметр прямоугольника
Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.
$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$
Читать дальше: формула периметра прямоугольника и примеры решений →
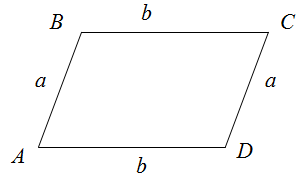
Периметр параллелограмма
Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.
$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$
Читать дальше: формула периметра параллелограмма и примеры решений →
Периметр трапеции
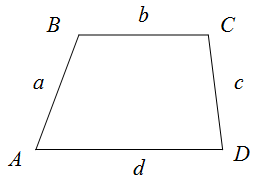
Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.
$$P_{Delta A B C D}=a+b+c+d$$
Читать дальше: формула периметра трапеции и примеры решений →
Периметр ромба
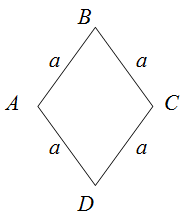
Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Читать дальше: формула периметра ромба и примеры решений →
Периметр эллипса
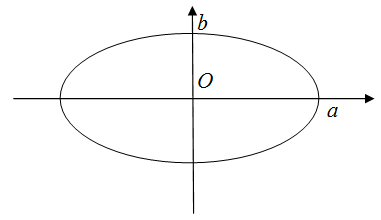
Чтобы найти периметр эллипса
$frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой
$$P=4 cdot frac{pi a b+(a-b)}{a+b}$$
Читать дальше: формула периметра эллипса и примеры решений →
- Как найти периметр треугольника
- Как найти периметр трапеции
- Как найти периметр ромба
- Как найти периметр эллипса
- Как найти периметр многоугольника
- Как найти периметр прямоугольного треугольника
- Как найти периметр равнобедренного треугольника
- Как найти периметр равностороннего треугольника
- Как найти периметр круга
- Как найти длину окружности
- Как найти периметр квадрата
- Как найти периметр прямоугольника
- Как найти периметр параллелограмма
Как найти периметр неправильной фигуры?
Для неправильного многоугольника, если все его стороны равны, мы можем вычислить его периметр, просто добавив длины всех его сторон.
Как найти периметр неправильного многоугольника?
Сложите значения всех сторон, чтобы найти периметр неправильного многоугольника. Просто сложите все значения, которые вы записали, и получите периметр многоугольника. В нашем примере с прямоугольником: 4 + 4 + 3 + 3 = 14 см — это периметр многоугольника.
Как найти периметр сложного прямоугольника?
Основная формула для вычисления периметра прямоугольника: P = 2 * (l + w). Запомните: периметр – это общая длина всех сторон фигуры….Умножьте эту сумму на два (согласно формуле).
- Обратите внимание, что умножив сумму на два, вы учли две другие стороны прямоугольника. …
- Полученное число будет периметром прямоугольника.
Как найти периметр фигуры 5 класс?
P = a + b + c, где a, b, c — длина стороны. Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три. P = 3 * a, где a — длина стороны.
Как найти периметр прямоугольника с разными сторонами?
Если дан многоугольник с разными длинами сторон, то общая формула периметра для него будет выглядеть, как сумма длин всех сторон: P=a1+a2+⋯+an , где ai – длина каждой конкретной стороны, а n – их количество.
Как вычислить периметр у прямоугольника?
Периметр прямоугольника — это сумма длины и ширины, умноженная на «2». , где «a» — длина прямоугольника, «b» — ширина прямоугольника.
Как найти периметр прямоугольника 2 класс задачи?
Делаем вывод: периметр прямоугольника – сумма длин всех его сторон. Чтобы найти периметр, надо измерить каждую сторону, а результаты сложить, или заменить сложение умножением как в способах номер 2 и 3.
Как найти периметр шестиугольника?
Чтобы найти периметр шестиугольника, измерьте и сложите длины всех его шести сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника, а а1, а2 … а6 – длины его сторон. Единицы измерения каждой из сторон приведите к одному виду – в этом случае достаточно будет сложить только числовые значения длин сторон.
Можно ли найти периметр окружности?
Формула для вычисления периметра круга (длины окружности) 1) Периметр круга равен произведению радиуса на два пи (3.
Как измерить длину окружности?
Чтобы найти длину окружности, нужно либо диаметр окружности умножить на π≈3,, либо найти удвоенное произведение радиуса и числа π. Здесь r — это радиус заданной окружности, а d — диаметр, π≈3,.
Как вычислить периметр эллипса формула?
Примеры вычисления периметра эллипса P=4⋅π⋅3⋅1+(3−1)3+1≈4⋅3,14⋅3+(ед.)
Что такое фокус эллипса?
Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек , называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: . При этом расстояния между фокусами меньше данного значения: .
Как построить эллипс по окружности?
Чтобы найти ось эллипса, делим вертикальную ось круга пополам и проводим через найденную точку еще одну ось. Видим, что данная линия не совпадает с осью круга. Теперь можно нарисовать эллипс. Делаем его симметричным относительно найденных осей и обрисовываем его, проходя через точки касания.
Как найти длину дуги овала?
Длину каждой дуги находят следующим образом. Сначала определяют периметр полных окружностей, частью которых являются дуги, составляющие овал. Периметры устанавливают по формуле 2πR, где π=3,14. Затем, разделив периметр малой окружности на 3 части, получают длину малой дуги.
Как найти площадь овала?
Формула для вычисления площади эллипса 1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.
Чему равна большая ось эллипса?
Большой осью эллипса называется его наибольший диаметр — отрезок проходящий через центр и два фокуса. Большая полуось составляет половину этого расстояния и идёт от центра эллипса через фокус к его краю.
Чему равно расстояние между фокусами эллипса?
Эллипсом называется плоская кривая, для каждой точки которой сумма расстояний до двух заданных точек (фокусов эллипса) постоянна. Расстояние между фокусами называется фокусным расстоянием и обозначается через 2c. Середина отрезка, соединяющего фокусы, называется центром эллипса.
Чему равна большая полуось?
Большая полуось орбиты Земли (среднее расстояние Земли от Солнца) — расстояние, принятое за астрономическую единицу. 1а. е. =± 0,7 км ≈ 149,6 млн.
Что такое малая ось эллипса?
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса. Точка пересечения большой и малой осей эллипса называется его центром.
Что такое эллипс?
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Что называется эллипсом?
П. I Эллипс. Определение: Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами и есть величина постоянная (ее обозначают через 2*а ). Причем эта постоянная больше расстояния между фокусами.
Чем эллипс отличается от окружности?
Овал – это замкнутая вытянутая геометрическая фигура, обладающая правильной формой и особыми свойствами. Вписанная в окружность, она обладает как минимум 4 точками экстремума, то есть вершинами. … Эллипс – это замкнутая плоская кривая, частный случай овала, у которого имеется 4 вершины в точках экстремума.
Как нарисовать эллипс и разместить внутри текста изменить формат в программе Word?
Ответ:
- Во вкладке «Вставка» найди «Фигуры», нажимаешь, в списке выбираешь «Овал» и растягиваешь до нужного размера.
- Жмешь правой кнопкой мыши на эллипс и выбираешь «Изменить текст».
- Точно так же правой кнопкой мыши и нажимаешь «Формат автофигуры».
Чем отличается круг и овал?
Самостоятельно обследуя модели фигур, рассматривая их, накладывая одну на другую, дошкольники должны попытаться сформулировать вывод об их сходствах и различиях: «Круг может катиться, ему ничего не мешает, а овал — нет, хотя у него углов нет. У овала одна часть широкая, а другая сужается, как у яйца».
Что такое окружность 3 класс?
Окружность — это замкнутая кривая, все точки которой одинаково удалены от центра. Круг – это геометрическая фигура, которая ограничена окружностью. Радиус- это отрезок, соединяющий центр окружности с любой точкой на окружности. Диаметр – отрезок, который соединяет две точки окружности, проходящий через центр.
Что называется хордой окружности?
Хо́рда (от греч. χορδή — струна) в планиметрии — отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
Чему равна касательная?
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку. … Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.