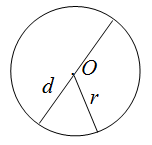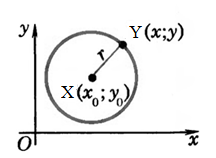Содержание:
- Формула
- Примеры вычисления периметра круга
Формула
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
$l=2 pi r$ или $l=pi d$
где $r$ и $d$ соответственно радиус и диаметр круга, а
$pi approx 3,1415926535 ldots$. Радиусом окружности называется отрезок,
соединяющий центр окружности с точкой окружности. Диаметр — это отрезок, который соединяет две точки окружности и проходящий
через её центр. Число $pi$ — математическая константа,
выражающая отношение длины окружности к длине её диаметра.
Примеры вычисления периметра круга
Пример
Задание. Найти периметр круга, радиус которого равен 2 см.
Решение. Периметр круга — это не что иное, как длина ограничивающей его окружности. Так как
нам задан радиус круга, то для вычисления длины окружности будем использовать формулу:
$l=2 pi r$
Получим:
$P_{k}=l=2 cdot pi cdot 2=4 pi approx 12,56$ (см)
Ответ. $P_{k}=4 pi approx 12,56$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Круг вписан в квадрат со стороной
$a=5$ мм. Найти периметр круга.
Решение. Сторона квадрата для круга является диаметром, то есть $a=d=5$ мм. Периметр круга равен длине окружности его
ограничивающей. Вычислим указанную длину по формуле:
$l=pi d$
Тогда искомый периметр равен:
$P_{k}=l=5 pi approx 15.7$ (мм)
Ответ. $P_{k}=l=5 pi approx 15.7$ (мм)
Читать дальше: как найти длину окружности.
Способы расчета периметра круга и длины окружности
Содержание:
- Периметр круга — что это, определение
-
Как рассчитать периметр круга или длину окружности
- Через радиус
- Через диаметр
- Примеры решения задач
Периметр круга — что это, определение
Определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Оределение
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Определение
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Определение
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно (pi=3,14159…)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
(pi=3,14)
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
(L=2pi R)
где (pi ) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
(L=pi D)
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
По формуле, (L= 2pi R). Отсюда:
(L=2pi R=2cdot0,5pi=piapprox3,14)
Ответ: 3,14 см.
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Решение
По формуле, (L=pi D). Отсюда:
(L=pi D=picdot2approx3,14cdot2=6,28)
Ответ: 6,28 см.
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
- Формула вычисления длины/периметра
- Примеры задач
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π:
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Формула периметра круга
Определение круга часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415 .
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(
Формула периметра круга
Периметр круга радиуса (r) :
[ LARGE
= 2 cdot pi cdot r ]
[ LARGE
= pi cdot d ]
( P ) – периметр (длина окружности).
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.
В декартовой системе координат ( xOy ) мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой ( X ) , которая будет иметь координаты ( (x_0,y_0) ) . Пусть радиус этой окружности равняется ( τ ) . Возьмем произвольную точку ( Y ) , координаты которой обозначим через ( (x,y) ) (рис. 2).
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
С другой стороны, ( |XY| ) — это расстояние от любой точки окружности до выбранного нами центра. То есть, по определению 3, получим, что ( |XY|=τ ) , следовательно
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Будем выводить длину произвольной окружности ( C ) с помощью её радиуса, равного ( τ ) .
Будем рассматривать две произвольные окружности. Обозначим их длины через ( C ) и ( C’ ) , у которых радиусы равняются ( τ ) и ( τ’ ) . Будем вписывать в эти окружности правильные ( n ) -угольники, периметры которых равняются ( ρ ) и ( ρ’ ) , длины сторон которых равняются ( α ) и ( α’ ) , соответственно. Как мы знаем, сторона вписанного в окружность правильного ( n ) – угольника равняется
Тогда, будем получать, что
Получаем, что отношение ( frac<ρ><ρ’>=frac<2τ> <2τ’>) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть ( n→∞ ) ), будем получать равенство:
Из последних двух равенств получим, что
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
Эту постоянную принять называть числом «пи» и обозначать ( π ) . Приближенно, это число будет равняться ( 3,14 ) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.
Вычислить периметр круга через:
Длина радиуса R:
Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.
Длина окружности всегда равна числу π (Пи)
Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…
Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.
Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».
Иными словами Пи ≈ 3,14 диаметрам круга или окружности.
Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна
P = D * π
или
P = 2 πR
где R –это радиус, а D – это диаметр
Как найти периметр круга
Формула
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
$l=2 pi r$ или $l=pi d$
где $r$ и $d$ соответственно радиус и диаметр круга, а $pi approx 3,1415926535 ldots$. Радиусом окружности называется отрезок, соединяющий центр окружности с точкой окружности. Диаметр — это отрезок, который соединяет две точки окружности и проходящий через её центр. Число $pi$ — математическая константа, выражающая отношение длины окружности к длине её диаметра.
Примеры вычисления периметра круга
Задание. Найти периметр круга, радиус которого равен 2 см.
Решение. Периметр круга — это не что иное, как длина ограничивающей его окружности. Так как нам задан радиус круга, то для вычисления длины окружности будем использовать формулу:
$P_=l=2 cdot pi cdot 2=4 pi approx 12,56$ (см)
Ответ. $P_=4 pi approx 12,56$ (см)
http://tamali.net/calculator/2d/circle/perimeter/
http://www.webmath.ru/poleznoe/formules_15_5.php
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Очевидно, что границей любого круга является окружность. Поэтому понятие периметра круга совпадает с таким понятием, как длина окружности. Поэтому вначале вспомним, что является окружностью, и какие понятия с ней связаны.
Понятие окружности
Определение 1
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Определение 2
Центром окружности будем называть точку, которая задается в рамках определения 1.
Определение 3
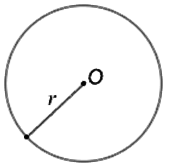
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
В декартовой системе координат $xOy$ мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой $X$, которая будет иметь координаты $(x_0,y_0)$. Пусть радиус этой окружности равняется $τ$. Возьмем произвольную точку $Y$, координаты которой обозначим через $(x,y)$ (рис. 2).
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
$|XY|=sqrt{(x-x_0)^2+(y-y_0)^2}$
«Как найти периметр круга» 👇
С другой стороны, $|XY|$ — это расстояние от любой точки окружности до выбранного нами центра. То есть, по определению 3, получим, что $|XY|=τ$, следовательно
$sqrt{(x-x_0)^2+(y-y_0)^2}=τ$
$(x-x_0)^2+(y-y_0)^2=τ^2$ (1)
Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.
Длина окружности (периметр круга)
Будем выводить длину произвольной окружности $C$ с помощью её радиуса, равного $τ$.
Будем рассматривать две произвольные окружности. Обозначим их длины через $C$ и $C’$, у которых радиусы равняются $τ$ и $τ’$. Будем вписывать в эти окружности правильные $n$-угольники, периметры которых равняются $ρ$ и $ρ’$, длины сторон которых равняются $α$ и $α’$, соответственно. Как мы знаем, сторона вписанного в окружность правильного $n$ – угольника равняется
$α=2τsinfrac{180^0}{n}$
Тогда, будем получать, что
$ρ=nα=2nτfrac{sin180^0}{n}$
$ρ’=nα’=2nτ’frac{sin180^0}{n}$
Значит
$frac{ρ}{ρ’}=frac{2nτsinfrac{180^0}{n}}{2nτ’frac{sin180^0}{n}}=frac{2τ}{2τ’}$
Получаем, что отношение $frac{ρ}{ρ’}=frac{2τ}{2τ’}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
$lim_{ntoinfty}(frac{ρ}{ρ’})=frac{2τ}{2τ’}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$lim_{ntoinfty}(frac{ρ}{ρ’})=frac{C}{C’}$
Из последних двух равенств получим, что
$frac{C}{C’}=frac{2τ}{2τ’}$
То есть
$frac{C}{2τ}=frac{C’}{2τ’}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
$C=2πτ$
Пример задач
Пример 1
Найти периметр круга, который вписан в квадрат со стороной, равной $α$.
Решение.
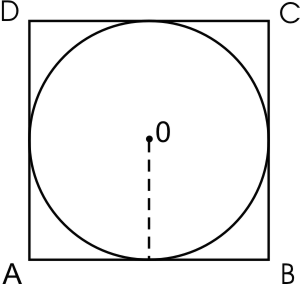
Пусть нам дан квадрат $ABCD$, в который вписана окружность с центром $O$. Изобразим рисунок по условию задачи (рис. 3).
Очевидно, что центр окружности будет совпадать с центром квадрата, в которой она вписана. Так как квадрат описан вокруг окружности, то его стороны будут касательными к ней, то есть радиус, проведенный, к примеру, к стороне $AB$ будет перпендикулярен к ней. Значит, диаметр окружности равняется стороне квадрата. То есть
$τ=frac{α}{2}$
По формуле периметра круга, получим, что
$C=2πcdot frac{α}{2}=πα$
Ответ: $πα$.
Пример 2
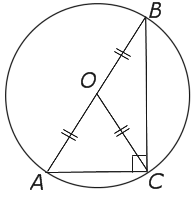
Найти периметр круга, который описан у прямоугольного треугольника с катетами, равными $α$ и $β$.
Решение.
Пусть нам дан треугольник $ABC$ с прямым углом $C$, у которой описана окружность с центром $O$. Как мы знаем, диаметром такой окружности является гипотенуза такого треугольника. То есть $|AO|=|OB|=|OC|=τ$ (рис. 4).
По теореме Пифагора, гипотенуза равняется
$|AB|=sqrt{α^2+β^2}$
То есть
$|AO|=τ=frac{sqrt{α^2+β^2}}{2}$
Периметр круга, по формуле, равняется
$C=2πcdot frac{sqrt{α^2+β^2}}{2}=πsqrt{α^2+β^2}$
Ответ: $πsqrt{α^2+β^2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме