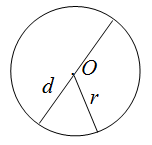В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
- Формула вычисления длины/периметра
- Примеры задач
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π:
C = π * d
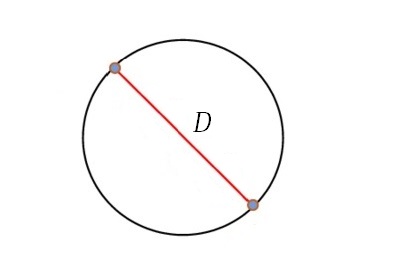
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Длина окружности. Площадь круга (Вольфсон Г.И.)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке вы вспомните, что такое окружность и круг, а также некоторые их элементы. Кроме того, вы познакомитесь с числом и двумя новыми формулами: формулой длины окружности и формулой площади круга, научитесь применять их при решении задач.
Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Точность и округление»
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Длина окружности или периметр круга
Вы можете установить этот калькулятор на свой сайт. Для этого используйте виджет.
Найти длину окружности, которую часто называют периметром круга, поможет наш калькулятор. Для расчета просто введите радиус или диагональ окружности и получите ответ в режиме онлайн. Также мы приводим формулы для расчета длины окружности самостоятельно.
Окружность — замкнутая плоская кривая у которой все ее точки удалены от данной точки (центра) на одинаковое расстояние и лежат с ней в одной плоскости.
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
http://mnogoformul.ru/dlina-okruzhnosti-ili-perimetr-kruga
Способы расчета периметра круга и длины окружности
Содержание:
- Периметр круга — что это, определение
-
Как рассчитать периметр круга или длину окружности
- Через радиус
- Через диаметр
- Примеры решения задач
Периметр круга — что это, определение
Определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Оределение
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Определение
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Определение
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно (pi=3,14159…)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
(pi=3,14)
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
(L=2pi R)
где (pi ) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
(L=pi D)
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
По формуле, (L= 2pi R). Отсюда:
(L=2pi R=2cdot0,5pi=piapprox3,14)
Ответ: 3,14 см.
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Решение
По формуле, (L=pi D). Отсюда:
(L=pi D=picdot2approx3,14cdot2=6,28)
Ответ: 6,28 см.
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Содержание:
- Формула
- Примеры вычисления периметра круга
Формула
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
$l=2 pi r$ или $l=pi d$
где $r$ и $d$ соответственно радиус и диаметр круга, а
$pi approx 3,1415926535 ldots$. Радиусом окружности называется отрезок,
соединяющий центр окружности с точкой окружности. Диаметр — это отрезок, который соединяет две точки окружности и проходящий
через её центр. Число $pi$ — математическая константа,
выражающая отношение длины окружности к длине её диаметра.
Примеры вычисления периметра круга
Пример
Задание. Найти периметр круга, радиус которого равен 2 см.
Решение. Периметр круга — это не что иное, как длина ограничивающей его окружности. Так как
нам задан радиус круга, то для вычисления длины окружности будем использовать формулу:
$l=2 pi r$
Получим:
$P_{k}=l=2 cdot pi cdot 2=4 pi approx 12,56$ (см)
Ответ. $P_{k}=4 pi approx 12,56$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Круг вписан в квадрат со стороной
$a=5$ мм. Найти периметр круга.
Решение. Сторона квадрата для круга является диаметром, то есть $a=d=5$ мм. Периметр круга равен длине окружности его
ограничивающей. Вычислим указанную длину по формуле:
$l=pi d$
Тогда искомый периметр равен:
$P_{k}=l=5 pi approx 15.7$ (мм)
Ответ. $P_{k}=l=5 pi approx 15.7$ (мм)
Читать дальше: как найти длину окружности.
периметр круга
Как найти периметр круга!? Формула периметра круга. Как на калькуляторе можно найти периметр круга!?
Наиболее часто встречающиеся словосочетания с периметром круга — радиус, диаметр, онлайн, калькулятор — разберем все темы!
О периметре круга.
- Формула периметра круга.
- Задача : найдите периметр круга если известен радиус.
- Задача : найдите диаметр круга, если известен периметр
- Периметр круга онлайн
Формула периметра круга.
Начнем с формулы периметра круга.
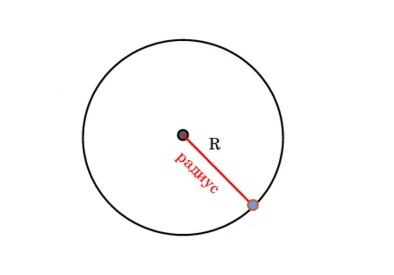
Формула круга может выражаться через радиус.
Формула периметра круга через радиус.
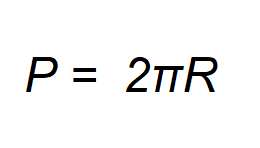
Где P — периметр круга,
π — число Пи.(3.14)
R — радиус круга.
Формула периметра круга через диаметр.
Также можно выразить периметр круга через диаметр. Поскольку мы занем, что диаметр = 2 радиуса, то в верхней формуле заменяем 2R на D.
Где P — периметр круга,
π — число Пи.(3.14)
D — диаметр круга.
Задача : найдите периметр круга если известен радиус.
Найдите периметр круга, если радиус круга равен 5см.

Такого рода задачки — это даже не задачки, это всего лишь одно действие с подстановкой данных.
Вместо буквы R ставим наш радиус, и далее нам все нужно перемножить, на калькуляторе
P = 2πR = 2π5 = 2 * 3.14 * 5 = 31.4
Ответ:
Найденный периметр круга равен 31.4 см.
Задача : найдите диаметр круга, если известен периметр круга
Условие задачи :
Найдите диаметр круга, если известен периметр круга, который равен 94.2см.
Для того, чтобы найти периметр круга, нам нужно из формулы выразить диаметр через периметр, что будет выглядеть так :
P = πD -> P/π = D -> D = P/π
Далее нам остается заменить букву P на значение из условия задачи 94.2см.
D = P/π -> D = 94.2/3.14 = 30см
Ответ:
Если периметр круга равен 94.2см, то искомый диаметр равен 30см.
Периметр круга онлайн
Для того, чтобы найти периметр круга онлайн, нужно заполнить соответствующее поле :
В поле нужно напечатать значение радиуса круга.
Нажмите найти периметр круга.
Не благодарите, но ссылкой можете поделиться!
COMMENTS+
BBcode