В этом уроке нам даны прямоугольники в координатной плоскости. Нам необходимо найти периметры и площади этих прямоугольников. Мы считываем координаты вершин этих прямоугольников и можем посчитать длины сторон прямоугольников из сетки.
Как только длина и ширина известны, мы можем найти периметры и площади этих прямоугольников.
В качестве альтернативы мы можем подсчитать количество единичных квадратов на сетке, чтобы найти области, и вдоль границы, чтобы найти периметры прямоугольников.
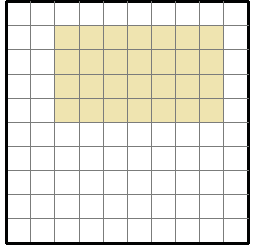
Найдите площадь и периметр следующего прямоугольника.
Решение
Step 1:
Площадь прямоугольника = l × w; l = длина = 5; ш = ширина = 4
Step 2:
Периметр прямоугольника = 5 + 4 + 5 + 4 = 18 единиц
Площадь прямоугольника = 5 × 4 = 20 квадратных единиц.
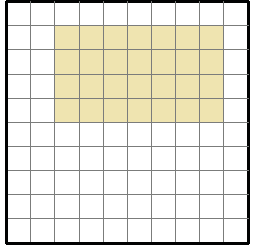
Найдите площадь и периметр следующего прямоугольника.
Решение
Step 1:
Площадь прямоугольника = l × w; l = длина = 7; ш = ширина = 4
Step 2:
Периметр прямоугольника = 7 + 4 + 7 + 4 = 22 единицы
Площадь прямоугольника = 7 × 4 = 28 квадратных единиц.
In this lesson, we are given rectangles in the coordinate plane. We are required to find the perimeters and the areas of these rectangles. We read the coordinates of the vertices of these rectangles and can count the lengths of the sides of the rectangles from the grid.
Once the lengths and widths are knows we can find the perimeters and areas of these rectangles.
Alternatively, we can count the number of unit squares on the grid to find the areas and along the boundary to find the perimeters of the rectangles.
Find the area and perimeter of the following rectangle.
Solution
Step 1:
Area of a rectangle = l × w; l = length = 5; w = width = 4
Step 2:
Perimeter of the rectangle = 5 + 4 + 5 + 4 = 18 units
Area of the rectangle = 5 × 4 = 20 square units.
Find the area and perimeter of the following rectangle.
Solution
Step 1:
Area of a rectangle = l × w; l = length = 7; w = width = 4
Step 2:
Perimeter of the rectangle = 7 + 4 + 7 + 4 = 22 units
Area of the rectangle = 7 × 4 = 28 square units.
|
Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам: Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим Ксарфакс 4 года назад Периметр по координатам Периметр фигуры — это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2): Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой:
Sadness 4 года назад Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так:l=sqrt((x2 — x1)^2 + (y2 — y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере:Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((12 — 1)^2 + ((-5) — 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((-2 — 12)^2 + (1 — -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 — (-2))^2 + (8 — 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты. Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым — просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула: , где х1 и х2 — координаты концов отрезка по оси х, а y1 и y2 — координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины. Hamster1337 2 года назад Периметр геометрических фигур по координатам вершин можно найти при помощи формулы Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр. Алиса в Стране 3 года назад Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр — сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула: где точка А имеет координаты (x1; y1), а точка В — координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС. габбас 4 года назад Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 — x1^2) + (y2^2 — y1^2), х1 и у1 координаты начала, х2,у2 — координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюминка 3 года назад Во-первых, вспомним, что такое периметр — это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb — xa)2 + (yb — ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2): Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить — получить. Бекки Шарп 3 года назад Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле: У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле. Складываем полученные результаты и получаем периметр. Бархатные лапки 3 года назад Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр. Знаете ответ? |
а) На координатной плоскости постройте прямоугольник ABCD по координатам его вершин:
A(5;3), B(−2;3), C(−2;−2), D(5;−2).
Вычислите периметр и площадь прямоугольника ABCD.
б) На координатной плоскости отметьте точки A(−8;3), B(1;3), C(1;−2).
Постройте четвертую точку D так, чтобы получился прямоугольник ABCD. Вычислите его периметр и площадь.
reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 11.5 Прямоугольные координаты на плоскости. Номер №985
Решение а
AD = BC = 5 (единиц);
AB = CD = 7 (единиц);
P = (AB + AD) * 2 = (7 + 5) * 2 = 12 * 2 = 24 (единицы);
S = AB * AD = 7 * 5 = 35 (квадратных единиц).
Решение б
AD = BC = 5 (единиц);
AB = CD = 9 (единиц);
P = (AB + AD) * 2 = (9 + 5) * 2 = 14 * 2 = 28 (единиц);
S = AB * AD = 9 * 5 = 45 (квадратных единиц).
-
Главная
-
ГДЗ
- 6 класс
- Математика
-
Мерзляк учебник
- 1308
Вернуться к содержанию учебника
Страница 275
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
Вопрос
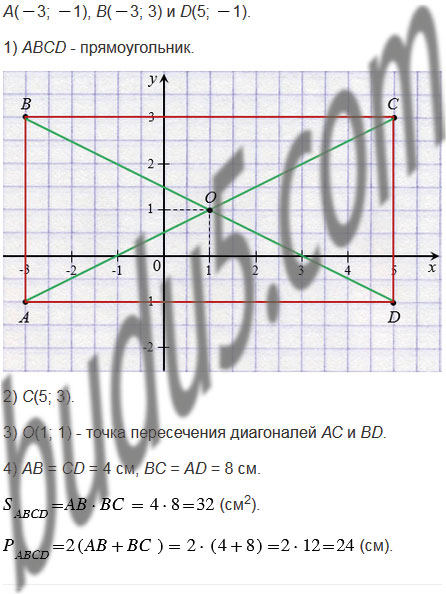
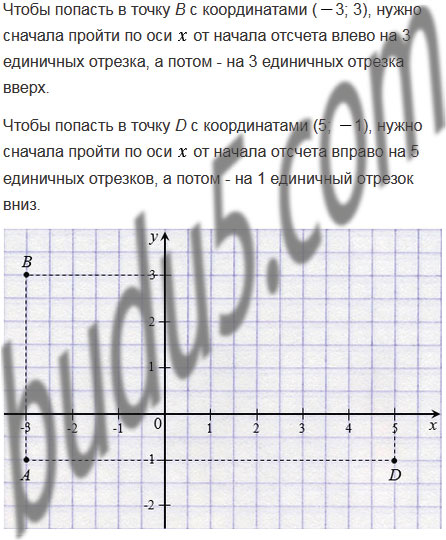
Даны координаты вершин прямоугольника АВСD: А(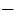
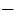
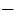
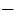
1) Начертите этот прямоугольник.
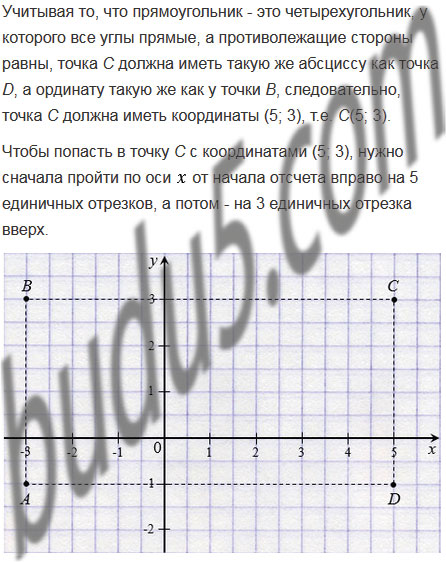
2) Найдите координаты вершины С.
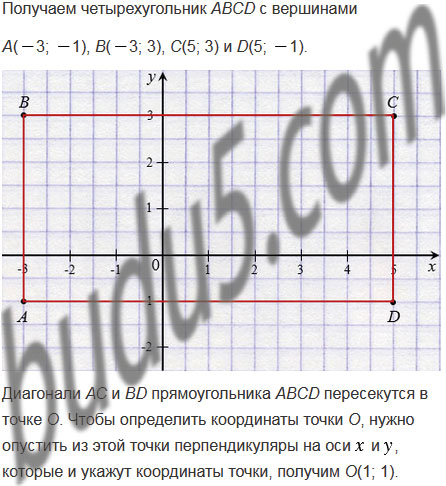
3) Найдите координаты точки пересечения диагоналей прямоугольника.
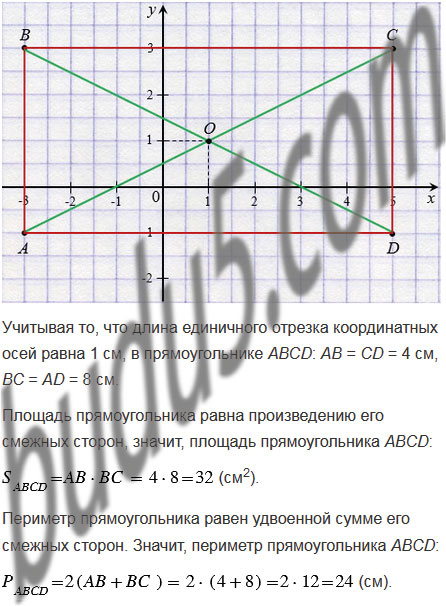
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
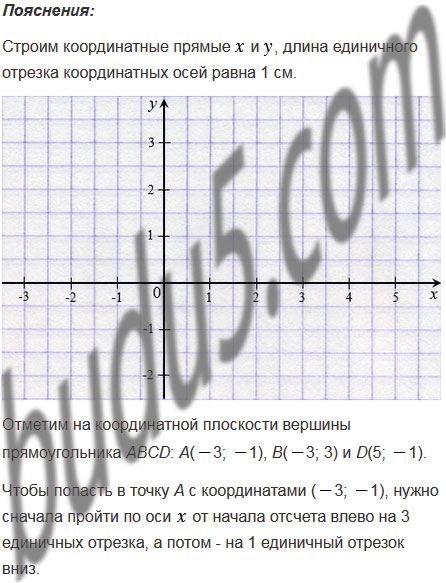
Подсказка
Вспомните:
- Что такое прямоугольник, как найти его площадь, периметр.
- Как определить положение точки на координатной плоскости.
Ответ
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
Вернуться к содержанию учебника