Среди геометрических фигур очень большую часть составляют многоугольники. Это квадрат, прямоугольник, параллелограмм, ромб, треугольник, трапеция и другие n-угольники (n — количество сторон многоугольника).
Периметр любого многоугольника – это сумма длин всех его сторон.
Онлайн-калькулятор периметра многоугольника
Формула периметра многоугольника
P=a+b+c+d+e+…P=a+b+c+d+e+…,
где a,b,c,d,e,…a, b, c, d, e,… — длины сторон многоугольника.
Частным случаем многоугольника является так называемый правильный многоугольник.
Правильный многоугольник – это такой многоугольник, у которого все стороны равной длины.
Если говорить о периметре правильного многоугольника, то его можно найти, умножив длину стороны фигуры на количество сторон.
P=n⋅aP=ncdot a
aa — длина стороны многоугольника;
nn — количество сторон многоугольника.
Разберем задачи на нахождение периметра правильного и неправильного многоугольников.
Найти периметр правильного шестиугольника со стороной 10 см.
Решение
a=10a=10
n=6n=6
Воспользуемся формулой для нахождения периметра правильного шестиугольника и подставим вместо aa численное значение:
P=n⋅a=6⋅10=60P=ncdot a=6cdot 10=60 см.
Ответ: P=60P=60 см.
Стороны многоугольника равны 6 см, 5 см, 2 см, 3 см и 1 см. Найти периметр данной фигуры.
Решение
a=6a=6
b=5b=5
c=2c=2
d=3d=3
e=1e=1
В данной задаче нам дан неправильный многоугольник, так как его стороны разной длины. В этом случае нам подходит первая стандартная формула нахождения периметра. Сложим длины всех сторон многоугольника и найдем его периметр:
P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17 см.
Ответ: P=17P=17 см.
Ищете, где где можно заказать контрольную работу недорого? Обратитесь к нашим экспертам!
Тест по теме “Периметр многоугольника”
|
Периметр шестиугольника так же вычисляется как и периметр треугольника, четырехугольника… Периметр- это сумма длин всех сторон геометрической фигуры. Измеряйте длину каждой стороны вашего шестиугольника, запишите данные и сложите их. система выбрала этот ответ лучшим Невозмутимый Дождь 2 года назад Шестиугольник обладает периметром, который исчисляется по такой же формуле, по которой учащийся ищет периметры пятиугольников или треугольников. Но в формуле, касающейся шестиугольника, учитывается число его сторон, равное шести. При равенстве сторон длина одной стороны умножается на 6. Например: длина одной стороны — 3 сантиметра. 3 X 6 = 18. Получается, периметр шестиугольника равен 18-ти сантиметрам при условии, если его каждая сторона равна 3-ем сантиметрам. Если у шестиугольника разные стороны, то предыдущий способ вычисления периметра не подойдет. Здесь просто нужно сложить все стороны. К примеру, стороны шестиугольника равны 2,3,4,5,6,7 сантиметрам. Тогда делаем так: 2 + 3 + 4 + 5 + 6 + 7 = 27. То есть периметр нашего неправильного шестиугольника будет равен 27-ми сантиметрам. З В Ё Н К А 2 года назад Периметры шестиугольников представляют собой суммы всех отрезков, каждый из которых равен длине одной из их сторон. Таким образом, мы должны будем условно обозначить для удобства каждый угол такого шестиугольника. Например, буквами. Это сделано будет для того, чтобы измерять и суммировать отрезки, не путая их. Теперь по формуле типа «а + б + в + г… = P» мы ищем число, которое будет соответствовать периметру данной шестиугольной геометрической фигуры. Шесть углов — это шесть сторон. Следовательно, у нам должно быть ровно шесть слагаемых. На рисунке вы видите шестиугольник, правильным не являющийся: Например:
Прежде всего вспомним, что периметр любого многоугольника представлется собой сумму длин всех его сторон. Это самая простая и универсальная формула, которая подходит для вычисления периметра фигур, начиная от тругольника и заканчивая n-угольником. Квадраты, ромбы, равносторонние и равнобедренные треугольники, прямоугольники и так далее тоже относятся к многоугольникам. В каждом из вышеприведенных примеров, так же как и в правильных многоульниках, формулу для вычисления периметра можно «усовершенствовать». В нашем случае, при условии, что шестиугольник является правильным, формула будет выглядеть следующим образом: P=6*a, где a — длина одной стороны. Если шестиугольник правильный, то для получения периметра надо умножить одну сторону на шесть. P = 6a. Также вокруг правильного шестиугольника можно нарисовать окружность. Радиус описанной окружности будет равен стороне. Потому, если по данным задачи известен радиус, то используем в формуле его. P = 6R. Если же по заданию окружность не описанная, а вписанная, то можно определить сторону правильно шестиугольника, исходя из радиуса. А уже после рассчитать периметр. a = 2r/√3. Если шестиугольник неправильный, то стороны будут отличаться и данные формулы применять нельзя. Тогда исходим уже из исходящих данных. ИнгаМус 8 лет назад Чтобы найти периметр шестиугольника, помню еще с уроков математики, надо знать длину каждой его стороны. Или просто измерить каждую его сторону. А затем надо сложить все полученные измерения и мы получим периметр. Анна Сергеевна 1984 8 лет назад Чтобы найти периметр многоугольника, нужно сложить длины его сторон. Валерий Альбертович 3 года назад Шестиугольники бывают разные, как и способы найти их периметры. Если речь идёт про правильный шестиугольник, то периметр будет вычисляться как длина стороны, умноженная на количество сторон, то есть в случае шестиугольника: P = 6*a, где а — сторона шестиугольника Если же шестиугольник, к примеру, неправильный, то достаточно просто сложить все его стороны, тогда получится периметр (это относится ко всем периметрам). bezdelnik 8 лет назад Шестиугольники могут быть разными: выпуклыми, с прямолинейными сторонами или с криволинейными, правильными у которого все стороны равны или неправильными. Периметр любого многоугольника равен сумме длин всех его сторон. Определенный ответ можно дать только о периметре правильного выпуклого прямолинейного шестиугольника вписанного в окружность с радиусом равным 1. Периметр такого шестиугольника равен 6-ти радиусам. валентин1943 8 лет назад Периметр правильного шестиугольника равен трём его центральным хордам, соединяющим противоположные вершины(или трём диаметрам описывающей шестигранник окружности).Если этот шестигранник неправильный и находится на пересеченной местности, то можно пройтись по его сторонам с шагомером. anna95 3 года назад Периметр шестиугольника можно найти так же как и у любой другой геометрической фигуры. Нужно измерить все его стороны и просто сложить, получившаяся сумма и будет периметром шестиугольника. Здесь ничего сложного нет. Знаете ответ? |
Download Article
Download Article
A polygon is any two-dimensional shape that has straight lines. There are both regular polygons, which are shapes with equal sides, and irregular polygons, which are shapes with different side lengths. The methods for finding the perimeter of regular and irregular polygons are a little different, but both are simple once you know what to do. You can also find the perimeter of them on a coordinate grid. If you’re trying to find the perimeter of a regular polygon, just use the formula: perimeter = number of sides x the length of any side.
-
1
Check that the sides of the polygon are all the same length. Regular polygons are polygons that have equal sides. If the sides of the polygon you’re looking at aren’t all the same length, you’ll need to find the perimeter using the method for irregular polygons instead. If the side lengths are equal, you’re working with a regular polygon.[1]
Tip: If some of the sides aren’t labeled, try looking at the rest of the polygon to determine what the lengths are. For example, if you have a square with only 1 labeled side, you know the other sides are the same length since squares have equal sides.
-
2
Write down the length of 1 side of the polygon. It doesn’t matter which side you choose since all of the side lengths are equal. Just make sure you’re only writing down the length of 1 side.[2]
- For example, if you’re working with a square that has a side length of 6, you would write down “6.”
Advertisement
-
3
Write down the total number of sides that the polygon has. Don’t worry about the side lengths at this point. Just count how many sides the polygon has and write it down.[3]
- For a square, you’d write down “4” since a square has 4 sides.
-
4
Multiply the side length by the number of sides to get the perimeter. The formula for finding the perimeter of a regular polygon is just the number of sides x the length of any side. Once you’ve multiplied those 2 numbers together, you’ve found the perimeter of the polygon![4]
- In the square example, you know that the square has a side length of 6 and a total of 4 sides. Therefore, you’d just multiply 6 by 4 to get 24, which would be the perimeter of the square.
- Or, say you were working with a triangle that has a side length of 3. Since a triangle has 3 sides, you would multiply 3 (the number of sides) by 3 (the side length) to get 9. Therefore, the perimeter of the triangle would be 9.
Advertisement
-
1
Look at the length of the polygon’s sides to determine if it’s irregular. An irregular polygon is a polygon that doesn’t have equal sides. If the sides of the polygon are all the same length, that means the polygon is regular, not irregular.[5]
Did you know? You can use the same method for finding the perimeter of an irregular polygon to find the perimeter of a regular polygon, but not the other way around.
-
2
Write down the length of each side of the polygon. Since not all sides of an irregular polygon are equal, you’ll need to write out each individual side length. Even if some of the sides are equal, you should still write each length out individually.[6]
- For example, if you’re working with a rectangle that has 2 sides that are 4 units long and 2 sides that are 3 units long, you would write “4, 4, 3, 3.”
- If you’re working with an irregular polygon that has 1 side that’s 2 units, 1 side that’s 3 units, and 1 side that’s 4 units, you would write “2, 3, 4.”
-
3
Add up all of the lengths to find the perimeter. To find the perimeter of an irregular polygon, all you need to do is find the total of all of its side lengths. Simply add up each side length that you wrote down to find the perimeter of the polygon![7]
- For example, if the side lengths for the polygon were 4, 4, 3, and 3, they would add up to 14. Therefore, 14 would be the perimeter of the polygon.
Advertisement
-
1
Draw a coordinate grid with an x- and y-axis. A coordinate grid is a graph with an x- and y-axis that you can plot coordinates on. To draw a coordinate grid, get a piece of graph paper or draw your own grid lines on a blank piece of paper using a ruler. Then, draw a horizontal line through the middle for the x-axis and a vertical line down the center for the y-axis. Finally, number the points on each axis, starting with “0” where the x- and y-axis intersect.[8]
- When you number your grid, the numbers above and to the right of the 0 will be positive, while the numbers below and to the left of the 0 will be negative.
-
2
Plot the given coordinates on the graph. You should have been given coordinates for each vertex, or angular point, of the polygon you’re trying to find the perimeter of. Each coordinate should look something like “(1,2).» Use the numbers you marked on the coordinate grid to plot each of the coordinates. When you’re finished, connect the points with straight lines to see the shape of the polygon you’re working with.[9]
Tip: When plotting coordinates, remember that the first number represents the x-axis and the second number represents the y-axis. For example, if you were plotting (2,4), you would count 2 over on the x-axis and 4 up on the y-axis and then mark where those 2 points meet on the grid.
-
3
Find vertical and horizontal side lengths by counting the units. You’ll need to know the length of each side of the polygon to determine its perimeter. For vertical or horizontal sides, simply count how many units there are between the points on each end. Then, write down the number next to that side so you can refer to it later.[10]
- For example, if you’re trying to find the length of a horizontal side, start at one end and count the number of boxes between that point and the other end. If you counted 6, that would mean the length of that side is 6 units.
-
4
Use the distance formula to find the length of diagonal sides. Unfortunately, you can’t count the units on a grid to find the length of diagonal sides like you can with vertical or horizontal sides. Instead, you’ll need to use the distance formula, which is
. Just plug in the values of the x and y coordinates for the 2 points at the ends of the side you’re trying to find the distance of and solve to find the length.[11]
-
5
Add the length of each side together to find the polygon’s perimeter. The perimeter of a polygon is equal to the sum of all of its side lengths. Once you’ve determined all of these lengths using the coordinates you were given, all you need to do is add them together and then you’re done!
- For example, if you plotted the coordinates of a triangle and found that the side lengths are 3, 2, and 5, you would add these numbers together to get 10. Therefore, the perimeter of the triangle is 10.
Advertisement
Add New Question
-
Question
What should I do when I don’t feel motivated to do homework?
Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.First, create a plan for doing the homework and build in breaks or rewards. For example, get one task done and then set a reward for yourself to take a 15-minute break to call a friend or to go outside for a walk.
-
Question
If I get stressed while studying, how can I stay positive so I can do better on exams?
Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.Build a positive reinforcement loop for yourself by having a plan. For example, take the test day and then work backwards from that and decide what things you need to get done during the time you have. Then work towards those things. It’s putting one foot in front of the other. It’s also being realistic. If you realize the plan is not possible, but you’ll still get through about 80% of it, you’re still going to probably do okay in the class. You’ve done the best that you can. It takes this weight off of your shoulders of having to be perfect. Instead, it’s I have to do the best that I can in any given circumstance and that’s all I can do.
-
Question
How do you find the perimeter and area of a polygon?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Support wikiHow by
unlocking this staff-researched answer.To find the perimeter, add up the lengths of all the sides of the polygon. Finding the area can be a little more complicated, since it depends on what kind of shape you’re dealing with. To calculate the area of a regular polygon, multiply ½ x p (the perimeter) x a (the apothem, or the distance from the center of the polygon to the midpoint of any side). If the polygon is irregular, you’ll need to divide it up into regular shapes (e.g., a rectangle and a triangle), find the area of each part, and add them together.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To find the perimeter of a regular polygon, which is a polygon with equal sides, start by writing down the length of 1 side and the total number of sides. Then, multiply those 2 numbers together to find the perimeter. If you’re trying to find the perimeter of an irregular polygon, which is a polygon with different side lengths, start by writing down the length of each side. Then, simply add up all of the lengths to find the perimeter. To learn how to find the perimeter of a polygon using coordinates, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 155,423 times.
Did this article help you?
Как найти периметр фигуры
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 +
× 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Формулы для расчета периметра шестиугольника
Иногда возникает необычная для учащегося задача по нахождению периметра шестиугольника. Не всегда на этот вопрос можно ответить сразу. В этой статье мы рассмотрим подробным образом, как найти периметр шестиугольника согласно формулам, а также вычислить и находить его другими способами.
Описание фигуры
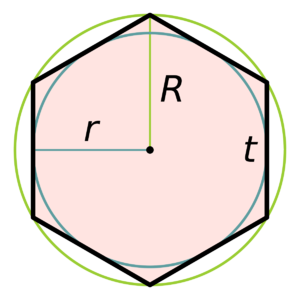
Непосредственно шестиугольник представляет собой плоскую фигуру, состоящую из шести отрезков, с расположением под углом 120 градусов относительно друг друга. Имеет научное название гексагон. Вокруг него или внутри можно вписать либо описать окружность. Между собой радиус и сторона многоугольника соотносятся по следующим формулам:
Гексагон является очень популярной фигурой, ее имеют гайки, карандаши, соты, снежинки и многое другое. Является оптимальным вариантом для того, чтобы без пробелов замостить все пространство. Одним из примеров этого является Мостовая гигантов, образовавшаяся в результате соединения более чем 40 тысяч базальтовых колонн в результате извержения древнего вулкана и элегантно замостившая поверхность побережья в Северной Ирландии.
Поиски вышеописанного параметра гексагона являются простой, но в то же время довольно интересной задачей. Найдя периметр, можно убедиться в правильности замощенного пространства и отсутствии пробелов при составлении будущей документации.
До начала вычислений
Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.
Первый вариант
Инструментарий достаточно простой. Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.
Например, имеются следующие отрезки: 2 сантиметра, 5,4,3,2 и 1 миллиметр. В этом случае нужно перевести 2 сантиметра в миллиметры из расчета 1 сантиметр равняется 10 миллиметрам и суммируете P=20+5+4+3+2+1=35 миллиметров. Таким образом рассчитывается периметр большинства видов шестиугольников.
Правильный шестиугольник
В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.
- Умножьте длину его стороны на 6 и вы получите нужное значение по формуле P=a*6, где a — сторона правильного шестиугольника.
- Например, у нас имеется фигура со стороной длиной 10 сантиметров, умножаем 10 на 6 и получаем в итоге 60 сантиметров в периметре.
- Также правильная фигура имеет уникальное свойство: радиус окружности, который описан вокруг такого шестиугольника, равен длине его стороны. Если вам известен радиус описанной окружности, то достаточно воспользоваться формулой в виде P=R*6, где R — радиус описанной окружности.
Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.
Иные варианты расчета
Если известен радиус вписанной в многоугольник окружности, рекомендуется использовать формулу P=4sqrt (3)*r, в которой r является радиусом вписанной окружности.
Можно высчитать периметр многоугольника, если в условии известна площадь. Площадь находится по формуле: S=3/2*sqrt (3)*a 2 , где S является площадью правильного шестиугольника. Далее находим из формулы a=sqrt (2/3*S/sqrt (3)). Найдя a, можно отыскать периметр, а именно P=6*a=6*sqrt (2/3*S/sqrt (3))=2*sqrt (2*s*sqrt (3)).
Другие способы измерения периметра шестиугольника можно найти в специализированной литературе и на особых порталах.
Шестиугольник относят к очень эффективной фигуре. Она встречается как в реальности, так и среди природных явлений. Если же вы боитесь, что не сможете правильно сами посчитать заданную величину, на помощь придут специальные онлайн-калькуляторы, в которых можно ввести необходимые данные для вычисления периметра. Удачной математической работы с поисками периметра для гексагона.
Видео
Посмотрите, как рассчитывается площадь правильного шестиугольника.
Периметр шестиугольника
Шестиугольник – это многоугольник, который имеет шесть углов.
Правильный шестиугольник – это выпуклый шестиугольник, у которого все углы и все стороны равны.
a – сторона правильного шестиугольника
A , B , C , D , E , F – вершины шестиугольника
Периметр правильного шестиугольника (P) равен сумме 6-ти его сторон ( a ) или:
http://liveposts.ru/articles/education-articles/matematika/formuly-dlya-rascheta-perimetra-shestiugolnika
http://formylu.ru/geometriya/formuly-perimetra/perimetr-shestiugolnika
В данной публикации мы рассмотрим, что такое периметр геометрической фигуры, как он считается, а также разберем примеры для демонстрации практического применения теоретических знаний.
- Определение периметра
- Формулы периметра распространенных фигур
- Примеры нахождения периметра
Определение периметра
Периметр – это сумма длин всех сторон геометрической фигуры (треугольника, квадрата, трапеции, ромба и т.д.).
Для измерения периметра используются единицы длины: миллиметры (мм), сантиметры (см), метры (м), километры (км) и т.д.
Общепринятое обозначение периметра – это латинская буква “P“, под которой можно добавить сокращенное название фигуры или ее обозначение. Например:
- Периметр треугольника можно записать как “Pтреуг.“ или “P△“;
- Периметр квадрата – “Pквадр.“ или “P□“
Формулы периметра распространенных фигур
Периметр произвольного многоугольника находится путем сложения длин всех его сторон.
Примеры нахождения периметра
Пример 1
Найдем периметр квадрата с длиной стороны 5 см.
Pквадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см.
Пример 2
Вычислим периметр прямоугольника с длиной 8 см и шириной 6 см.
Pпрямоуг. = 6 + 8 + 6 + 8 = (6 + 
Пример 3
Найдем периметр шестиугольника ниже.
P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28.