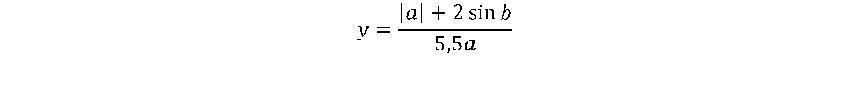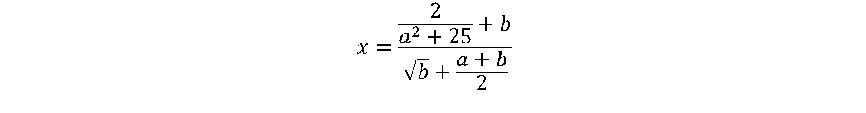Цель урока: продолжить формирование
навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания,
редактирования, форматирования и выполнения
простейших вычислений в электронных таблицах. - развивающие: расширить представления
учащихся о возможных сферах применения
электронных таблиц; развивать навыки
аналитического мышления, речи и внимания. - воспитательные: формировать и воспитывать
познавательный интерес; прививать навыки
самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
Ход урока
1. Организационный момент.
Сообщить тему урока, сформулировать цели и
задачи урока.
Сегодня мы вновь окажемся в гостях у маленького
великана Васи в Сказочной стране. Ему, как всегда,
требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы
вам известны? - Как задается имя ячейки (строки, столбца) в
электронной таблице? - Что может быть содержимым ячейки?
- Число 1 находится в столбце …, в строке …, в
ячейке с адресом … - Число 4 находится в ячейке с адресом …
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в
ячейке С1? - Чему равно значение, вычисляемое по формуле, в
ячейке D2?
2) Какой результат будет получен в ячейках с
формулами?
| А | В | |
| 1 | 25 | 4 |
| 2 | 2 | =A1*B1/2 |
| 3 |
Ответ: 25*4/2=50
| A | B | C | D | |
| 1 | 5 | 2 | 1 | |
| 2 | 6 | 8 | 3 | |
| 3 | 8 | 3 | 4 | |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил
домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований |
|||||||
| Среднее время участников соревнований |
|||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится
как среднее арифметическое трех его заплывов. - В ячейку «Лучшее время» записывается
минимальный результат из 3 заплывов. - В ячейку «Лучший результат соревнований»
записывается минимальное время из столбца. - В столбец «Отклонение» записывается
разность между лучшим временем спортсмена и
лучшим результатом соревнований. - В ячейку «Максимальное отклонение»
записывается максимальное значение столбца.
| Результаты соревнований по плаванию |
|||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований |
3,16 | ||||||
| Среднее время участников соревнований |
3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать
забор вокруг своего огорода и вскопать его под
посадку овощей (наступила очередная весна),
разметить грядки прямоугольной формы. Для работы
ему потребовалось найти длину забора и площадь
участка. Но ведь в школе он никогда не учился.
Поможем Васе.
№ 1. Вычислить периметр и площадь
прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для
следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно
решает следующую задачу и представляет свое
решение учащимся (через проектор).
№ 2. Маленький великан Вася решил
подсчитать, через сколько дней в его копилке
будет 100 руб., если ежедневно он стал класть туда
на 5 руб. больше, чем в предыдущий день. Помогите
Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению
следующей.
Один ученик показывает, как работать с
формулами, другой – как использовать функцию
суммирования, числовой формат (общий, денежный) и
т.д. (Таблица уже готова, ученикам предстоит
ввести формулы, использовать суммирование и
получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли
Васе 150 рублей, чтобы купить все продукты, которые
ему заказала мама, и хватит ли на чипсы за 10
рублей? Сдачу мама разрешила положить в копилку.
Сколько рублей попадет в копилку?
Предполагаемое решение:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
|
Итого: |
=СУММ(E2:E5) | |||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется |
=D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у
жителей Цветочного города.
Собираясь на пляж, веселые человечки решили
запастись прохладительными напитками. Незнайка
взял с собой 2 литра кваса, 1 литр газировки и 1
литр малинового сиропа, Пончик – 3 литра
газировки и 2 литра малинового сиропа, Торопыжка
– 2 литра газировки, доктор Пилюлькин – 1 литр
кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все
человечки вместе? - Сколько всего литров напитков взял с собой
каждый из человечков? - Сколько всего литров напитков взяли все
человечки вместе?
Оформите таблицу произвольно и сохраните в
своей личной папке.
Результат работы.
| Веселые человечки. Напитки. |
|||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.

Подумайте и решите эту задачу, если известны
еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе
стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр
малинового сиропа – 6 монет, 1 литр касторки – 2
монеты.
- Сколько монет истратил на покупку напитков
каждый человечек? - Сколько монет затрачено на покупку напитков
каждого вида? - Сколько потрачено денег всеми человечками
вместе?
Литература
- Информатика. Задачник-практикум в 2 т. /Под ред.
И.Г.Семакина, Е.К.Хеннера – М.: Лаборатория
Базовых Знаний, 2010. - Ефимова О. Курс компьютерной технологии с
основами информатики. – М.: ООО “издательство
АСТ”; АВF, 2005.
Презентация
Для квадрата со стороной a периметр P можно
вычислить с помощью следующих формул
Переходим к
формулам для двух огородов в форме прямоугольников. Обозначим через b меньшую сторону прямоугольника, а через q отношение его сторон (для первого прямоугольника q=2, для второго – q=3).
Тогда формулы для вычисления периметра в случае прямоугольника можно записать
так
Рассмотрим теперь формулы для выбора самого короткого забора вокруг
четырех огородов. Пусть i – порядковый номер огорода, Pi – периметр i — го
огорода, Pmin – искомый минимальный
периметр. Тогда можно написать формулу
Обозначим буквой T – форму огорода с
самым коротким забором и напишем формулу для ее автоматического вычисления
Легко проверить, что условия задачи позволяют выполнить расчеты по
формулам (3.1)-(3.5) и найти решение поставленной задачи.
3.4. Описание решения задачи
Фрагмент рабочего листа Excel с решением
задачи об огородах (см. рис. 3.1) дает пример возможного оформления результатов
вычислений.
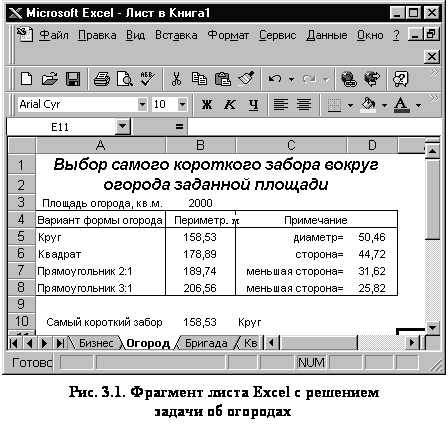 |
Ввод и форматирование заголовка произведено так, как описано в
задачах о платежной ведомости и об оптимальном бизнесе. Заданная площадь
огородов введена в ячейку B3. Расчеты, связанные с
определением длины заборов вокруг огородов, представлены в табличной форме в
ячейках интервала A4:D8. Первая
колонка таблицы представляет варианты формы огородов. Длина заборов (периметры),
вычисленная по формулам (3.1)-(3.3), видна во втором столбце таблицы.
Вспомогательные величины вычислены в ячейках интервала D5:D8 и вместе с кратким пояснением в ячейках C5:C8 образуют третий столбец таблицы (см. рис. 3.1). Например,
для квадрата в ячейку D6 введена формула =КОРЕНЬ(B3), обеспечивающая вычисление стороны, а в ячейку B6 формула =4*D6 для вычисления
периметра. Копирование этих формул в другие ячейки не производилось, поэтому в
них можно использовать ссылки на ячейки любого типа. Основу указанных двух
формул составляют формулы (3.2) из подраздела 3.3.
Наибольший интерес представляют формулы в ячейках B10
и C10. В ячейку B10 введена
формула =МИН($B$5:$B$8),
реализующая вычисление минимального периметра Pmin
по формуле (3.4). Более сложна формула в ячейке C10
=ЕСЛИ(B5=B10;A5;ЕСЛИ(B6=B10;A6;ЕСЛИ(B7=B10;A7;A8)))
Она реализует выбор варианта формы огорода с минимальным периметром
в точном соответствии с формулой (3.5). Пояснения по использованию логической
функции ЕСЛИ имеются в подразделе 2.4.
3.5. Выводы
Результаты решения задачи соответствуют известному математическому
факту: чем более «правильную» форму имеет плоская фигура заданной площади, тем
меньше ее периметр. Периметры огородов в форме круга, квадрата и двух прямоугольников
(см. рис. 3.1) увеличиваются по мере уклонения их формы от «правильной».
Наименьший периметр 158,53 м имеет огород в форме круга. Наибольший периметр
206,56 м у прямоугольника с отношением сторон 3:1. Следовательно, по
сравнению с круглым огородом забор для второго прямоугольного огорода на
48,03 м длиннее. Соответственно увеличиваются затраты на его
строительство.
На практике круглые огороды не очень распространены. Поэтому из
трех других вариантов формы следует выбрать квадрат, у которого периметр
меньше, чем у остальных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Формулы периметра и программы для расчета периметра
Основные свойства квадрата
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC ┴ BD | AO = BO = CO = DO = | d |
| 2 |
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Как посчитать периметр помещения
Периметр – это длина геометрической фигуры по её внешней границе.
Периметр помещения – это сумма длин сторон помещения. Соответственно для вычисления периметра необходимо суммировать все стороны.
Формула расчета периметра помещения:
А – длина помещения;
В – ширина помещения;
Для помещения произвольной конфигурации используются более сложные формулы расчета и этот расчет быстрее и удобнее выполнить с применением чертежных программных продуктов.
В нашей проектной организации Вы можете заказать расчет периметра помещения на основании технологического или конструкторского задания. Расчет выполним для любой конфигурации по Вашему рисунку с применением самых современных чертежных программ 2D-черчения.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета периметра помещения. С помощью этого калькулятора в один клик вы можете вычислить периметр помещения, если известны длина и ширина.
Что необходимо знать о квадрате?
Прежде чем приступать к проведению вычислений, необходимо знать некоторые важные сведения об этой фигуре, среди которых:
- все стороны квадрата равны;
- все углы квадрата прямые;
- площадь квадрата – это способ исчисления того, как много места занимает фигура в двухмерном пространстве;
- двухмерное пространство – это лист бумаги или экран компьютера, где нарисован квадрат;
- периметр не является индикатором наполненности фигуры, однако позволяет работать с его сторонами;
- периметр – это сумма всех сторон квадрата;
- подсчитывая периметр, мы оперируем одномерным пространством, что означает фиксацию результата в метрах, а не метрах квадратных (площадь).
Как вычислить периметр
Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).
Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.
Периметр и площадь прямоугольника
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:
P= (a+b)*2
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.
Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
S= a*b
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.
Свойства квадрата.
– у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
– противолежащие стороны квадрата параллельны:
– каждый уг ол квадрата прямой:
– сумма углов квадрата равна 360°:
– каждая диагональ квадрата имеет такую же длину, как и другая:
– каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
– угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
– точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей .
– все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
– диагонали делят квадрат на 4 одинаковых треугольника , кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Периметры фигур
Расчет периметра квадрата, прямоугольника, треугольника, круга (периметры фигур).
Периметры фигур
Площадь квадрата
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Формулы определения площади квадрата
3. Формула площади квадрата через диагональ квадрата:
5. Формула площади квадрата через диаметр описанной окружности:
8. Формула площади квадрата через длину отрезка l :
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата :
3. Формула диагонали квадрата через периметр квадрата :
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7. Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности :
R – радиус вписанной окружности;
D – диаметр вписанной окружности;
d – диагональ квадрата.
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
Периметр квадрата. Площадь квадрата.
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Радиус вписанной окружности – сторона квадрата (половина).
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Круг, описанный вокруг квадрата – это круг, который проходит через 4-ре вершины квадрата и который имеет центр на пересечении диагоналей квадрата.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Электронные таблицы
Электронные таблицы
Электронные таблицы
Постройте электронную таблицу, которая автоматически вычисляет площадь и периметр прямоугольника по его сторонам:
Постройте электронную таблицу для расчёта стоимости бензина, необходимого для поездки на автомобиле:
Постройте электронную таблицу, которая автоматически вычисляет площадь всех стен комнаты по её размерам:
Оформление электронных таблиц
Перейдите в каталог work-27 и откройте файл excel. xls (или excel. ods). Закончите оформление таблиц на листах 1, 2 и 3 в соответствии с заданиями, записанными далее.
Во всех задачах этой работы выделяйте жёлтым фоном все ячейки, в которых находятся исходные данные; серым фоном – ячейки с промежуточными результатами вычислений и зелёным фоном – ячейки с основными результатами решения задачи.
Выполните задание 12 из рабочей тетради.
Перейдите на Лист 1 открытой рабочей книги. Удалите лишние строки и столбцы. Оформите электронную таблицу, которая рассчитывает стоимость покупок в магазине. При печати она должна выглядеть следующим образом:
Выполните задание 13 из рабочей тетради.
Перейдите на Лист 2 открытой рабочей книги. Оформите электронную таблицу для расчёта семейного бюджета. При печати она должна выглядеть следующим образом:
Выполните задание 14 из рабочей тетради.
Перейдите на Лист 3 открытой рабочей книги. Постройте электронную таблицу для расчёта оплаты за квартиру:
Перейдите в каталог work-28 и откройте файл salary. xls (или salary. ods).
Вычислите суммарную, минимальную, максимальную и среднюю зарплату по каждой группе сотрудников фирмы. Установите для всех ячеек, содержащих денежные суммы, денежный формат (только рубли, без копеек). Вычислите суммарную, минимальную, максимальную и среднюю зарплату в целом по предприятию. Используйте вызовы функций с несколькими аргументами-диапазонами. Сортировка
Перейдите в каталог work-29 и откройте файл exam. xls (или exam. ods).
Используя сортировку, ответьте на вопросы: У скольких учащихся фамилия начинается с буквы «З»? Сколько в списке учащихся из Майского района? Кто из учащихся получил высший балл по русскому языку? Используя сортировку, ответьте на вопросы: Сколько процентов учащихся получили 41 балл по математике? Сколько учащихся сдали русский язык выше, чем на 50 баллов? Сколько процентов от общего числа учащихся составляют жители Заречного района? Используя сортировку, ответьте на вопросы: Сколько процентов из учащихся Майского района получили 18 баллов по математике? Кто из учащихся Подгорного района получил лучший балл по русскому языку? Кто из учащихся, получивших 38 баллов по математике, получил лучший балл по русскому языку? Относительные и абсолютные ссылки
Перейдите в каталог work-30 и откройте файл premia. xls (или premia. ods).
Заполните столбцы Премия и Зарплата. При вычислении премии нужно использовать значения ячейки B1. Определите минимальную, максимальную, среднюю и суммарную зарплату по каждому цеху и по всему заводу в целом. Перейдите на Лист 2. Заполните таблицу по расчёту цен на планшетные компьютеры и подсчитайте общую выручку магазина. Диаграммы
Перейдите в каталог work-31 и откройте файл diagram. xls (или diagram. ods).
Как рассчитать площадь прямоугольника, треугольника или круга в Excel
Известно, что геометрия упрощает математику и вычисления. Площадь основных форм, таких как прямоугольник, треугольник и круг, можно вычислить с помощью определенных формул. Если вам нужно рассчитать площадь основных фигур для диапазона записей, Excel будет очень полезен. В этой статье мы объяснили процедуру вычисления площадей прямоугольника, круга и треугольника в Excel.
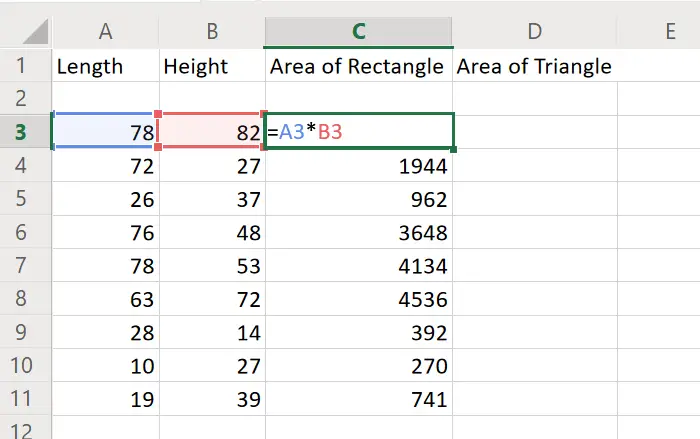
Вычислить площадь прямоугольника в Excel
Основная формула для вычисления площади прямоугольника в Excel: длина * высота. Таким образом, синтаксис формулы для определения площади прямоугольника в Excel будет выглядеть так:
Например. Предположим, у нас есть список длин прямоугольников, распределенных по столбцу A от ячейки A3 до A11, и высоты прямоугольников, распределенных по столбцу B от B3 до B11. Нам нужна площадь прямоугольника в столбце C от C3 до C11.
Теперь формула прямоугольника для C3 будет выглядеть так:
Вы можете использовать функцию Fill, чтобы переместить формулу до C11. Просто щелкните за пределами ячейки C3 и вернитесь к ней. Затем используйте кнопку заполнения в правом нижнем углу, чтобы сдвинуть выделение до C11.
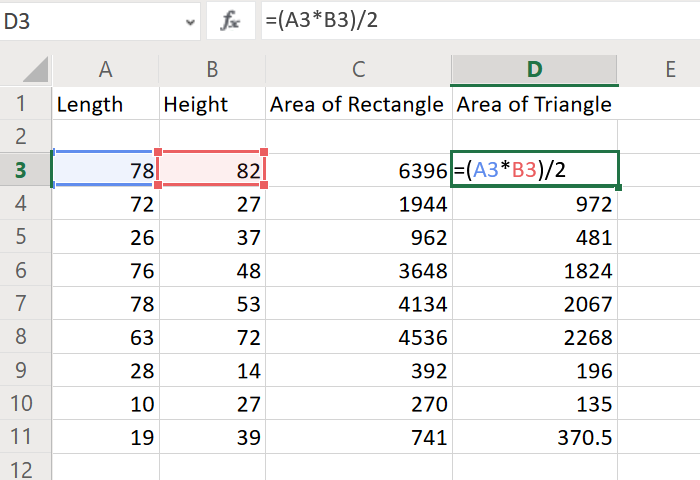
Вычислить площадь треугольника в Excel
Формула для вычисления площади треугольника: (длина * высота) / 2. Таким образом, синтаксис формулы для определения площади треугольника в Excel будет выглядеть так:
Например. Давайте рассмотрим длину и высоту в столбцах A и B, как в предыдущем примере. Нам нужны площади треугольников в столбце D от D3 до D11.
Теперь формула для треугольников для C3 будет выглядеть так:
Вы можете использовать функцию Fill, как объяснялось ранее, чтобы перенести формулу до D11.
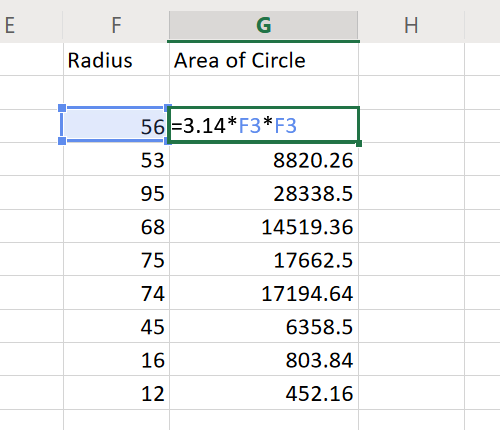
Вычислить площадь круга в Excel
Площадь круга равна 3,14 * (радиус * радиус). Чтобы создать формулу в Excel, я мог бы предложить экспоненциальную функцию, однако, поскольку цель состоит в том, чтобы просто найти квадрат, мы можем немного изменить формулу. Синтаксис поиска площади круга в Excel выглядит следующим образом:
Например, если у нас есть список радиусов в столбце F от F3 до F11 и нам нужны площади кругов в столбце G от G3 до G11, тогда формула для ячейки G3 будет выглядеть так:
Вы можете использовать функцию Fill, чтобы перетащить формулу в ячейку G11.
http://pandia.ru/text/81/520/49830.php
Как рассчитать площадь прямоугольника, треугольника или круга в Excel
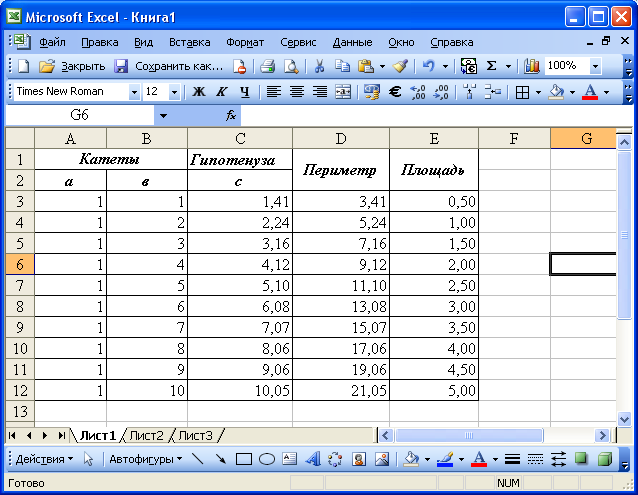
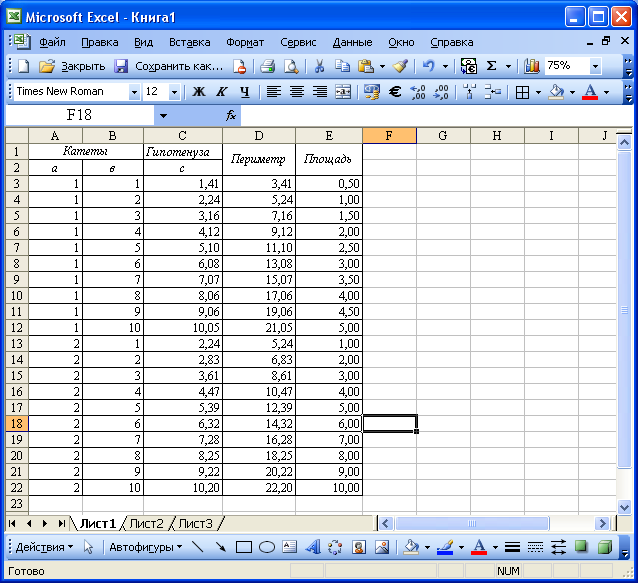
Построить таблицу
значений периметра и площади прямоугольного
треугольника при изменении длин его
катетов от 1см до 10см с шагом 1см.
Периметр
прямоугольного треугольника вычисляется
по формуле:
где a,b,
— катеты, c
–гипотенуза, которая вычисляется по
формуле:
Площадь прямоугольного
треугольника вычисляется по формуле:
Для решения задачи
построим шапку таблицу:
-
А
В
С
D
E
1
Катеты
Гипотенуза
Периметр
Площадь
2
a
b
c
3
4
Теперь занесем
формулы. В столбец А
занесем значения катета a=1,
в столбец
В – значения
катета b
от 1до 10 с шагом 1.
-
А
В
С
D
E
1
Катеты
Гипотенуза
Периметр
Площадь
2
a
b
c
3
1
1
4
1
2
5
1
3
6
1
4
7
1
5
8
1
6
9
1
7
10
1
8
11
1
9
12
1
10
В ячейку С3
запишем формулу, вычисляющую гипотенузу:
=КОРЕНЬ(А3^2+B3^2),
в ячейку D3
запишем формулу: =A3+B3+C3,
в ячейку
E3
запишем формулу:
=(1/2)*A3*B3
-
А
В
С
D
E
1
Катеты
Гипотенуза
Периметр
Площадь
2
a
b
c
3
1
1
=КОРЕНЬ(А3^2+B3^2)
=A3+B3+C3
=(1/2)*A3*B3
4
1
2
…
12
1
10
Теперь скопируем
формулы третьей строки во все остальные
строки
(Рис. 89.). Отформатируем формат
представления чисел до 2 знаков после
запятой.
Заметим, что во
всех формулах используются относительные
адреса ячеек.
Рис. 89. Решение
задачи 2
Теперь добавим
строки, в которых катет a
будет равен 2 (Рис. 90.), не забывая копировать
в них формулы.
Рис. 90. Решение
задачи 2 с добавление данных
Так же можно
добавить строки с другими значениями
катета a.
Соседние файлы в предмете Информатика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на использование математических функций
Операцию возведения в степень не использовать
-
Известна сторона квадрата. Подготовить лист для расчета его площади.
|
A |
B |
C |
|
|
1 |
Задайте сторону квадрата |
||
|
2 |
Площадь квадрата равна: |
||
|
3 |
|||
|
4 |
-
Известна площадь квадрата. Оформить лист для расчета его стороны.
-
Известна площадь круга. Оформить лист для определения его диаметра.
-
Даны катеты прямоугольного треугольника. Подготовить лист для расчета его гипотенузы. Решение оформить в виде:
|
A |
B |
C |
|
|
1 |
|||
|
2 |
Задайте первый катет |
||
|
3 |
Задайте второй катет |
||
|
4 |
Гипотенуза равна: |
-
Даны стороны прямоугольника. Оформить лист для расчета его диагонали.
-
Известна длина стороны равностороннего треугольника. Оформить лист для определения его высоты.
-
Оформить лист для расчета среднего геометрического двух заданных целых чисел.
-
Даны стороны прямоугольного параллелепипеда. Оформить лист для определения его диагонали.
-
Считая, что Земля – идеальная сфера с радиусом R≈6350 км, определить расстояние от точки, с заданной высотой над Землей до линии горизонта.
-
Оформить лист для расчета периметра прямоугольного треугольника по известным катетам.
-
Известна площадь квадрата. Оформить лист для расчета его диагонали.
-
Даны стороны треугольника. Оформить лист для определения его площади.
-
Известны координаты двух точек на плоскости. Оформить лист для вычисления расстояния между ними.
-
Даны основания и высота равнобедренной трапеции. Подготовить лист для вычисления ее периметра.
-
Треугольник задан координатами своих вершин. Подготовить лист для вычисления его периметра и площади.
-
Подготовить лист для расчета синуса, косинуса, тангенса и котангенса угла, значение которого будет вводиться в одну из ячеек. Рассмотреть 2 варианта:
-
значение угла указывается в радианах;
-
значение угла указывается в градусах.
-
-
Подготовить лист для определения абсолютной величины числа, значение которого будет вводиться в одну из ячеек.
-
Известна диагональ квадрата. Оформить лист для расчета его площади и периметра.
-
Подготовить лист для определения площади ромба по известной длине его стороны и значению внутреннего угла в градусах.
-
Даны стороны параллелограмма и значение одного из внутренних углов (в градусах). Подготовить лист для определения площади параллелограмма.
-
Даны стороны треугольника и угол между ними (в градусах). Подготовить лист для определения площади треугольника.
-
Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для определения периметра треугольника. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
-
Известны размеры большего основания и боковой стороны равнобедренной трапеции, а также угол при большем основании. Подготовить лист для определения периметра трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
-
Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для вычисления площади треугольника.
-
Подготовить лист для определения угла по известному значению его:
-
Синуса;
-
Косинуса;
-
Тангенса;
-
Котангенса.
-
Во всех случаях определить величину угла в радианах и градусах.
-
Известны длины сторон равнобедренного треугольника. Подготовить лист для вычисления его внутренних углов (в градусах).
-
Известны размеры оснований и боковой стороны равнобедренной трапеции. Подготовить лист для вычисления угла (в градусах) при большем основании.
-
Даны стороны a, b, c треугольника. Подготовить лист для вычисления его углов (в градусах) по теореме косинусов:
A=arcos(b2 + c2 – a2)/2bc
-
Даны катеты прямоугольного треугольника. Подготовить лист для вычисления острых углов треугольника (в градусах).
-
Даны основание и высота равнобедренного треугольника. Подготовить лист для вычисления угла (в градусах) при основании.
-
Известны размеры диагоналей ромба. Подготовить лист для вычисления его внутренних углов (в градусах).
-
Даны координаты на плоскости двух точек. Подготовить лист для вычисления угла наклона к оси абсцисс прямой, соединяющей эти точки.
-
Подготовить лист для нахождения десятичного логарифма числа, которое будет указываться в одной из ячеек.
-
Подготовить лист для нахождения натурального логарифма числа, которое будет указываться водной из ячеек.
-
Подготовить лист для вычисления значений eπ и πe.
-
Дана гипотенуза прямоугольного треугольника, а также один из его острых углов (в градусах). Подготовить лист для вычисления катетов этого треугольника.
-
Известна длина диагонали прямоугольника, а также угол ее наклона к большей стороне прямоугольника. Оформить лист для расчета площади и периметра прямоугольника.
-
Известны размеры большего основания и боковой поверхности равнобедренной трапеции, а также угол при большем основании. Подготовить лист для вычисления периметра и площади трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
-
Оформить лист для расчета значения функций
при данных значениях a и b
-
Считая, что Земля – идеальная сфера с радиусом R ≈ 6350 км, подготовить лист для определения расстояния до линии горизонта от точки с высотой над Землей, равной 1, 2, …, 10 км.
-
Получить на листе 10 первых чисел Евклида. Числа Евклида вычисляются по формуле:
Ek = 2k-1(2k-1), k = 1, 2, 3, …
-
Получить на листе 8 первых чисел ферма. Числа Ферма вычисляются следующим образом:
Fk = 2A+1, A = 2k+1, k = 1, 2, 3, …
-
Подготовить на листе таблицу значений функции y = sin(x), где х меняется от 0 до 6,5 радиан с шагом 0,5.
-
Получить на листе таблицу значений sin2, sin3, …, sin20 (значения углов указаны в радианах.
-
Получить на листе таблицу значений tg5, tg6, …, tg15 (значения углов указаны в радианах).
-
Получить на листе таблицу значений тригонометрических функций y = sin(x/2),
y = sin(2x), y = cosx для x, равного 00, 200, 400, …, 7200.
-
Пусть функция y(x) задана таблицей:
|
x |
y |
|
x1 |
y1 |
|
x2 |
y2 |
|
… |
… |
|
xn |
yn |
Значения аргумента х расположены в порядке возрастания, но не обязательно равномерно. Предположим, что точки (хi, уi) последовательно соединены отрезками прямых линий. Угловым коэффициентом каждого отрезка называется дробь:
(yi-1 — yi)/ (xi-1 — xi)
Оформить лист, на котором для каждого отрезка определить:
-
Его угловой коэффициент;
-
Угол наклона к горизонтали (в градусах).
-
Около стены наклонно стоит палка длиной 4,5 м. Один ее конец находится на расстоянии 3 м от стены. Нижний коней палки начинает скользить в плоскости, перпендикулярной стене. Оформить на листе таблицу для определения значения угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0,2 м.
-
Плотность воздуха убывает с высотой по закону p=p0e—bz, где p – плотность на высоте b метров, p0 =1,29 кг/м3, z=1,25*10-4. Получить на листе таблицу зависимости плотности от высоты для значений от 0 до 1000 м через каждые 100 м.
-
Получить на листе значения sin1, sin1+sin2, sin1+ sin2+sin3, …, sin1+sin2+…+ sin10. Значения получить в ячейках B2:B11, введя формулу только в одну ячейку и распространив (скопировав) ее на остальные ячейки диапазона.
A
B
C
1
2
1
0,841471
3
2
1,750768
4
3
1,891888
5
4
1,135086
6
5
0,176162
7
6
-0,10325
8
7
0,553733
9
8
1,543091
10
9
1,955209
11
10
1,411188
12
-
Получить на листе значения 1/ sin1, 1/( sin1+sin2), …, 1/(sin1+sin2+…+ sin10).
-
Значения получить С2:С11, введя формулу только в ячейки В2 и С2 и распространив (скопировав) их на остальные ячейки диапазона В2:С11.
|
A |
B |
C |
D |
|
|
1 |
||||
|
2 |
1 |
1,188395 |
||
|
3 |
2 |
0,571178 |
||
|
4 |
3 |
0,528572 |
||
|
5 |
4 |
0,880991 |
||
|
6 |
5 |
5,676604 |
||
|
7 |
6 |
-9,68487 |
||
|
8 |
7 |
1,805925 |
||
|
9 |
8 |
0,64805 |
||
|
10 |
9 |
0,511454 |
||
|
11 |
10 |
0,708623 |
||
|
12 |
-
Получить на листе значения cos1/sin1, (cos1+ cos2, )/ (sin1+sin2), …,( cos1+…+ cos15)/( sin1+…+ sin15).
Значения получить в ячейках F2:F11, введя формулы только в ячейки второй строки и распространив (скопировав) их на остальные ячейки диапазона В2: F11.
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
|||||||
|
2 |
1 |
0,642093 |
|||||
|
3 |
2 |
0,070915 |
|||||
|
4 |
3 |
-0,45766 |
|||||
|
5 |
4 |
-1,33865 |
|||||
|
6 |
5 |
-7,01525 |
|||||
|
7 |
6 |
2,669616 |
|||||
|
8 |
7 |
0,863691 |
|||||
|
9 |
8 |
0,215641 |
|||||
|
10 |
9 |
-0,29581 |
|||||
|
11 |
10 |
-1,00444 |
|||||
|
12 |
Литература:
Д.М. Златопольский. Задачник по Excel, 2002, №24. Информатика