Нахождение периметра квадрата
Определение
Квадрат – это такой четырехугольник, который обладает свойствами прямоугольника, параллелограмма, а также ромба:
- Все стороны равны.
- Все углы прямые, то есть по 90°.
- Диагонали равны, а угол их пересечения прямой.
- Диагонали при пересечении делать эти углы пополам.
Зная свойства квадрата, можно понять, что его периметр находится путем сложения всех 4 сторон или же умножения его одной стороны на 4. Из этого выведем формулу где a – сторона квадрата:
[P = a + a + a + a]
[P = 4a]
Пример 1
Найдите периметр квадрата, сторона которого равна 6 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + a + a
6 + 6 + 6 + 6 = 24 (см)
Ответ: периметр этого квадрата равен 24 см.
Пример 2
Найдите периметр квадрата, сторона которого равна 10 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 4a
4 × 10 = 40 (см)
Ответ: периметр равен 40 см.
Нахождение периметра прямоугольника
Определение
Прямоугольник – это геометрическая фигура, которая может быть квадратом, прямоугольником или же ромбом.
Характеристики:
- У прямоугольника все углы по 90°
- В отличие от квадрата, у прямоугольника равны только противолежащие стороны, которые являются его шириной и высотой. Эти стороны параллельны. Из этого следует, что каждый квадрат – прямоугольник, но квадратом являются не все прямоугольники.
- Его прилегающие стороны перпендикулярны во всех случаях.
- Если провести диагональ, то она поделит прямоугольник на два равных прямоугольных треугольника.
- Если мы имеем две диагонали, то можно утверждать, что они одинаковой длины.
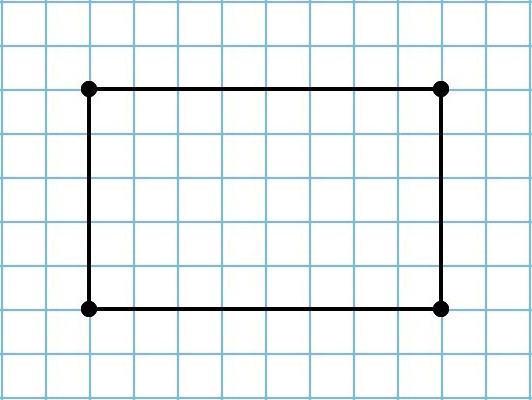
Периметр прямоугольника – это сумма длин всех его сторон. Получается, чтобы найти его периметр, воспользуемся формулами, в которых a – ширина и b – высота:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Пример 1
Найдите периметр прямоугольника, стороны которого равны 8 и 4 см.
Решение:
Воспользуемся формулой и подставим числа:
P = a + a + b + b
8 + 8 + 4 + 4 = 24 (см)
Ответ: периметр этого прямоугольника равен 24 см.
Пример 2
Найдите периметр прямоугольника, стороны которого равны 10 и 12 см.
Решение:
Теперь используем вторую формулу и подставим числа:
P = 2(a + b)
2(10 + 12) = 44 (см)
Ответ: периметр равен 44 см.
Пример 3
Найдите периметр прямоугольника, стороны которого равны 9 и 7.
Решение:
На очереди третья формула. Подставим числа и решим:
P = 2a + 2b
2 × 9 + 2 × 7 = 32 (см)
Ответ: периметр равняется 32 см.
Нахождение периметра параллелограмма
Определение
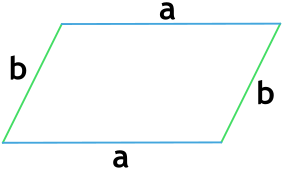
Параллелограмм – это такой четырехугольник, у которого противоположные стороны парно параллельны.
Характеристики:
- Противоположные стороны равны.
- Противоположные углы равны.
- Диагонали в точке пересечения делятся пополам.
- Как и в прямоугольнике, диагональ параллелограмма делит его на 2 треугольника.
- Два угла на одной стороне равны 180°
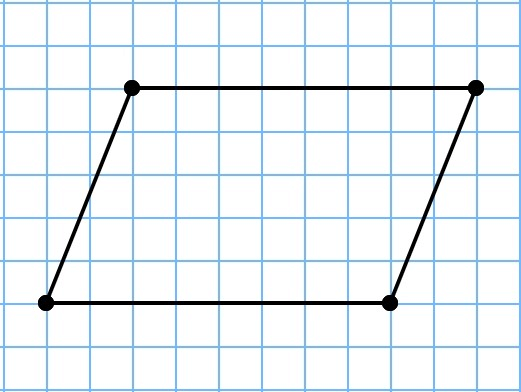
Периметр параллелограмма находится точно так же, как и периметр прямоугольника:
[P = a + a + b + b]
[P = 2(a + b)]
[P = 2a + 2b]
Нахождение периметра трапеции
Формула
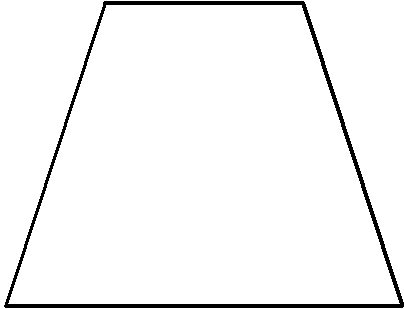
Трапеция – это четырехугольник, отличающийся тем, что его две стороны параллельны, а другие две не параллельны.
Характеристики:
- Основа трапеции – это те две параллельные стороны.
- Боковые стороны – не параллельные стороны.
- Если две боковые стороны равны, то можно сделать вывод, что такая трапеция равнобедренная.
- Трапеция с прямыми углами является прямоугольной.
- В трапеции можно провести среднюю линию, которая будет параллельна основаниям, а также равняться их полусумме.
- Если трапеция равнобедренная, то ее углы и длины диагоналей равны.
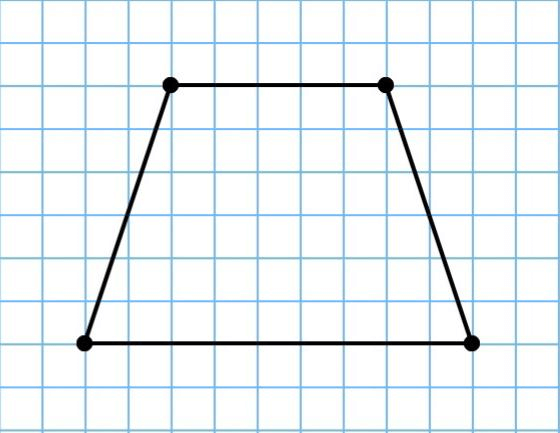
Формула
Чтобы найти периметр трапеции, необходимо знать длины всех ее сторон, чтобы сложить их. Представим, что
стороны трапеции – это a, b, c, d. Получается, для нахождения периметра трапеции, нам надо сложить все ее
стороны:
[P = a + b + c + d]
Пример 1
Найдите периметр трапеции, если известно, что ее стороны равны: 2, 6, 5, 5.
Решение:
Используем формулу:
P = a + b + c + d
2 + 6 + 5 + 5 = 18 (см)
Ответ: периметр трапеции равен 18 см.
Нахождение периметра ромба
Определение
Ромб – это четырехугольник, являющийся параллелограммом с равными сторонами.
Характеристики:
- Стороны и высоты ромба равны.
- Углы диагоналей при пересечении равны 90° — эти углы прямые.
- Диагональ является биссектрисой и делит углы пополам.
- Ромб называется параллелограммом, так как он имеет те же свойства, что и параллелограмм.
- В каждый ромб можно вписать окружность.
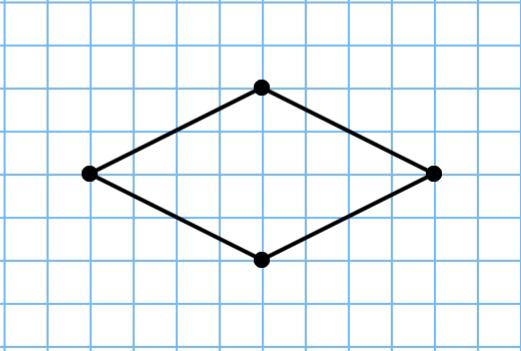
Ромб – это квадрат, а это значит, что найти его периметр можно так, как и периметр квадрата:
[P = a + a + a + a]
[P = 4a]
Нет времени решать самому?
Наши эксперты помогут!
Нахождение периметра многоугольника
Определение
Многоугольник – это геометрическая фигура, которая со всех сторон ограничена ломанной линией.
Характеристики:
- Название многоугольника определяется количеством его вершин. Если у многоугольника количество вершин равно n, то он называется n-угольником.
- Многоугольником являются такие фигуры, как: квадрат, ромб, параллелограмм и т.д.
- Если углы с отрезками равны, то это правильный многоугольник.
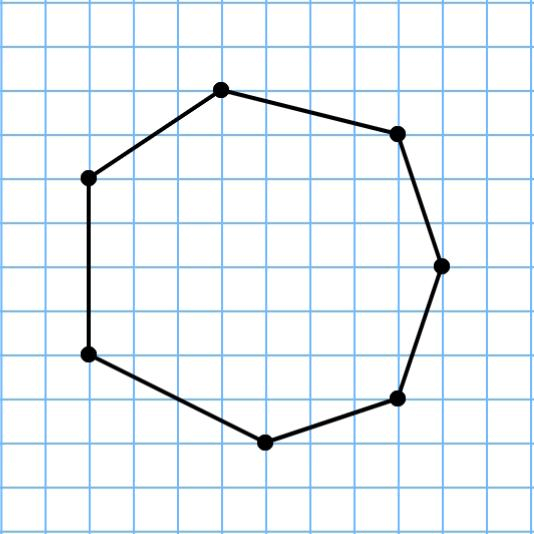
Чтобы найти периметр n-угольника, нужно сложить всего длины его сторон:
[P = a1 + a2 + … an]
А для правильного n-угольника можно выделить еще одну формулу, потому как его стороны равны:
P = na
Здесь мы умножаем длину одной стороны на n.
Пример 1
Найдите периметр правильного многоугольника, если у него 5 вершин, а длина его одной стороны равна 7.
Решение:
Здесь воспользуемся этой формулой:
P = na
7 × 5 = 35 (см)
Ответ: периметр многоугольника равняется 35 см.
Нахождение периметра эллипса
Определение
Эллипс это замкнутая кривая, находящаяся на плоскости. Ее получают с помощью пересечения цилиндра плоскостью.
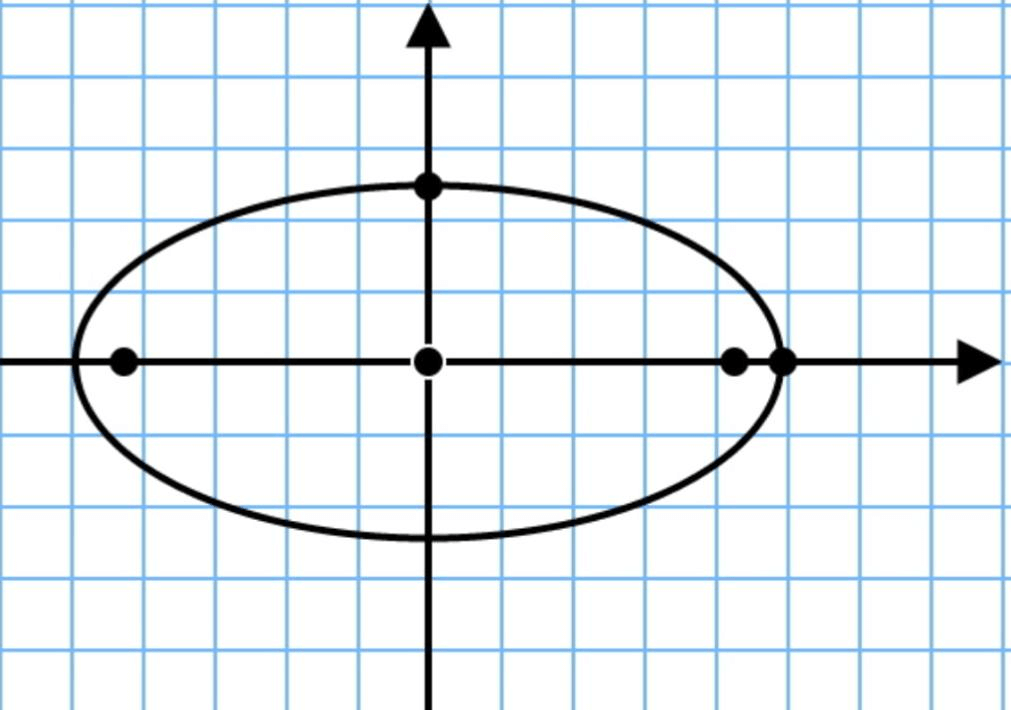
Для нахождения периметра, нужно следовать формуле:
[P=4 pi a b+a-b / a+b]
Калькулятор периметр квадрата
Что такое периметр параллелограмма
Периметр параллелограмма — это сумма длин всех его сторон.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.
Свойства
- противоположные стороны равны и параллельны;
- противоположные углы попарно равны;
- сумма соседних углов равна 180 градусов;
- сумма всех углов равна 360 градусов;
- диагонали фигуры делятся пополам в точке пересечения;
- точка пересечения диагоналей — центр симметрии параллелограмма;
- биссектриса образует равнобедренный треугольник.
Как найти периметр
Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По сумме всех сторон
Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем формулу:
P=2(a+b),
где a и b — это две смежные стороны данного четырехугольника.
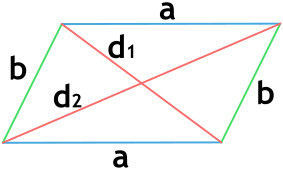
По стороне и двум диагоналям
Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:
(a=frac{sqrt{2d_1^2+2d_2^2-4b^2}}2,)
где (d_1) и (d_2) — это обе диагонали фигуры.
Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b).)
По стороне, высоте и синусу угла
В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:
(a=frac{h_b}{sinalpha})
где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.
Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:
(P=2(frac{h_b}{sinalpha}+b))
Примеры решения задач
Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.
Задача 1
Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.
Решение:
Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.
Ответ: 28 см.
Задача 2
Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.
Решение:
Для расчета суммы длин всех сторон используем формулу:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b))
Подставляем известные значения:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(frac{sqrt{2times6^2+2times8^2-4times4^2}}2+4)=2(frac{sqrt{72+128-64}}2+4)=2(frac{2sqrt{34}}2+4)=2sqrt{34}+8) см.
Ответ:( 2sqrt{34}+8) см.
Задача 3
Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6). Найти сумму длин всех сторон фигуры.
Решение:
Для расчета будем использовать уравнение:
(P=2(frac{h_b}{sinalpha}+b))
Подставим известные величины:
(P=2(frac1{sin{displaystylefracpi6}}+2)=2(frac1{displaystylefrac12}+2)=8;)см.
Ответ: 8 см.
В данной публикации мы рассмотрим, каким образом можно посчитать периметр параллелограмма и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
Периметр (P) параллелограмма равняется сумме длин всех его сторон. А т.к. противоположные стороны данной фигуры равны, формулу можно представить в следующем виде:
P = 2 * (a + b) или P = 2a + 2b
Примеры задач
Задание 1
Найдите периметр параллелограмма, если его стороны равны 6 и 8 см.
Решение:
Воспользуемся одной из двух формул выше, подставив в нее известные значения: P = 2 * 6 см + 2 * 8 см = 28 см.
Тот же самый результат получится, если применить вторую формулу: P = 2 * (6 см + 8 см) = 28 см.
Задание 2
Периметр параллелограмма равен 50 см. Найдите его вторую сторону, если известно, что первая равна 7 см.
Решение:
Нам известно, что периметр считается по формуле: P = 2a + 2b.
Допустим a – это известная сторона, и нам нужно найти b. Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см.
Следовательно, длина неизвестной стороны составляет: b = 36 см / 2 = 18 см.
Периметр параллелограмма зависит от длины его сторон. И хотя формула для расчета несложная, мы сделали калькулятор, который позволяет рассчитать периметр параллелограмма в режиме онлайн. Наш калькулятор рассчитает периметр параллелограмма по двум сторонам или по двум диагоналям и одной из сторон.
Содержание:
- калькулятор периметра параллелограмма
- формула периметра параллелограмма через две стороны
- формула периметра параллелограмма через диагонали и одну из сторон
- примеры задач
Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны.
На сайте вы можете рассчитать периметры других четырехугольников: квадрат, ромб, прямоугольник.
Формула периметра параллелограмма через две стороны
{P = 2 (a + b)}
a и b — стороны параллелограмма
Формула периметра параллелограмма через диагонали и сторону
{P = 2a+ sqrt{2{d_1}^2 + 2{d_2}^2 — 4a^2}}
или
{P = 2b+ sqrt{2{d_1}^2 + 2{d_2}^2 — 4b^2}}
a и b — стороны параллелограмма
d1 и d2 — диагонали параллелограмма
Примеры задач на нахождение периметра параллелограмма
Задача 1
Найдите периметр параллелограмма со сторонами 3см и 4.5см.
Решение
Так как из условия задачи мы знаем длины сторон, то воспользуемся первой формулой. Подставим в нее значения длин сторон и произведем расчет:
P = 2 (a + b) = 2 (3 + 4.5) = 2 (7.5) = 15 : см
Ответ: 15см
Воспользуемся калькулятором для проверки полученного ответа.
Задача 2
Найдите периметр параллелограмма, если его стороны равны 5см и 80мм.
Решение
Для начала переведем 80мм в сантиметры и получим, что 80мм = 8см. В остальном задача аналогична предыдущей, так что повторим процесс ее решения:
P = 2 (a + b) = 2 (5 + 
Ответ: 26см
Для проверки снова используем калькулятор . При этом мы можем не переводить 80мм в сантиметры, а просто задать длину стороны в миллиметрах.
Анна Кирпиченкова
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Периметр любой геометрической фигур на плоскости определяется как сумма длин всех его сторон. В этой статье, на примере задач, мы приведем формулы для нахождения периметров квадрата, прямоугольника, параллелограмма, трапеции, ромба, многоугольника и эллипса.
Периметр квадрата
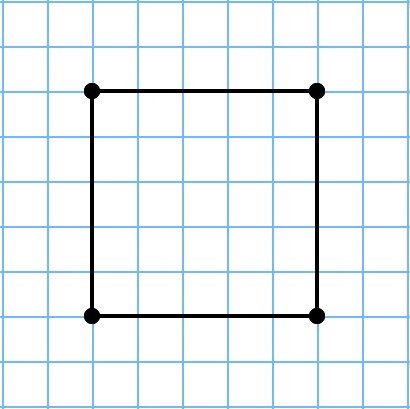
Определение 1
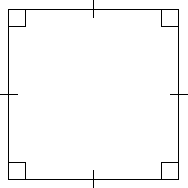
Квадратом будем назвать такую геометрическую фигуру, которая состоит из четырех равных сторон, все углы которой прямые (рис. 1).
Пример 1
Найти периметр квадрата, если его сторона равняется $α$.
Решение.
Так как все 4 стороны квадрата равны между собой, то, по определению периметра, получим
$P=α+α+α+α=4α$
Вывод: Для нахождения периметра квадрата надо длину его стоны умножить на $4.$
Периметр прямоугольника
Определение 2
Прямоугольником будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой, все углы которой прямые (рис. 2).
Пример 2
Найти периметр прямоугольника, если его смежные стороны равняются $α$ и $β$.
Решение.
Так как противоположные стороны равняются между собой, то
$P=α+α+β+β=2α+2β=2(α+β)$
«Как найти периметр квадрата, прямоугольника, параллелограмма, трапеции, ромба, эллипса, многоугольника» 👇
Вывод: Для нахождения периметра прямоугольника надо сумму длин его смежных сторон умножить на $2.$
Периметр параллелограмма
Определение 3
Параллелограммом будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем противоположные стороны равны между собой и параллельны друг другу (рис. 3).
Пример 3
Найти периметр параллелограмма, если его смежные стороны равняются $α$ и $β$.
Решение.
Так как противоположные стороны равняются между собой, то
$P=α+α+β+β=2α+2β=2(α+β)$
Вывод: Для нахождения периметра параллелограмма надо сумму длин его смежных сторон умножить на $2.$
Периметр трапеции
Определение 4
Трапецией будем назвать такую геометрическую фигуру, которая состоит из четырех сторон, причем 2 противоположные стороны, которые называются основаниями, параллельны друг другу (рис. 4).
Пример 4
Найти периметр трапеции, если его стороны равняются $α$, $β$, $γ$ и $δ$.
Решение.
По определению периметра плоской геометрической фигуры получим, что
$P=α+β+γ+δ$
Вывод: Для нахождения периметра трапеции надо сложить все длины его сторон.
Периметр ромба
Определение 5
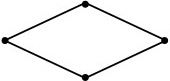
Ромбом будем назвать такой параллелограмм, у которого все стороны равны между собой (рис. 5).
Пример 5
Найти периметр ромба, если его сторона равняется $α$.
Решение.
Так как все 4 стороны ромба равны между собой, то, по определению периметра, получим
$P=α+α+α+α=4α$
Вывод: Для нахождения периметра ромба надо длину его стоны умножить на $4.$
Периметр многоугольника
Отметим, что все фигуры, рассмотренные выше, являются многоугольниками, а именно четырехугольниками. Поэтому можем рассмотреть более обще понятие, а именно понятие -угольника.
Определение 6
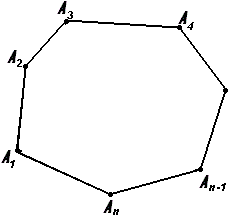
$n$-угольником будем назвать такую геометрическую фигуру, которая состоит из $n$ непересекающихся сторон и $n$ углов. (рис. 6).
Пример 6
Найти периметр $n$-угольника, если его стороны равняются $α_1$, $α_2$,…, $α_n$.
Решение.
По определению периметра плоской геометрической фигуры получим, что
$P=α_1+α_2+⋯+ α_n$
Вывод: Для нахождения периметра -угольника надо сложить все длины его сторон.
Здесь можно выделить периметр правильного $n$-угольника, то есть $n$-угольника, у которого все стороны равняются между собой.
Пример 7
Найти периметр правильного $n$-угольника, если его сторона равняется $α$.
Решение.
Так как все $n$ сторон правильного $n$-угольника равны между собой, то, по определению периметра, получим
$P=α+α+⋯+α+α$ — $n$ раз.
Следовательно
$P=nα$
Вывод: Для нахождения периметра правильного $n$-угольника надо длину его стороны умножить на $n$
Периметр эллипса
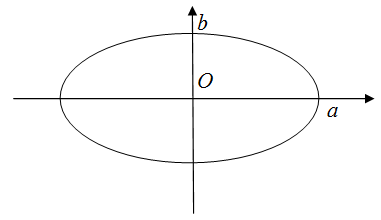
Здесь просто введем формулу, для вычисления периметра (или еще иначе длины) эллипса. Пусть нам дан эллипс, как на рисунке 7.
Тогда периметр эллипса равняется
$P=4frac{πab+a-b}{a+b}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме