Как найти периметр прямоугольной трапеции 8 класс

Как найти периметр прямоугольной трапеции

Трапеция — четырехугольник с двумя параллельными основаниями и не параллельными боковыми сторонами. Прямоугольная трапеция имеет прямой угол при одной боковой стороне.

Инструкция

Периметр прямоугольной трапеции равен сумме длин сторон двух оснований и двух боковых сторон. Задача 1. Найдите периметр прямоугольной трапеции, если известны длины всех его сторон. Для этого сложите все четыре значения: P (периметр) = a + b + c + d.Это самый простой вариант нахождения периметра, задачи с другими начальными данными, в конечном итоге, сводятся к ней. Рассмотрим варианты.

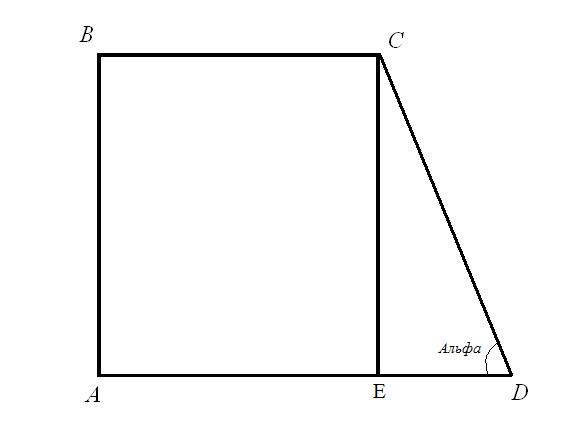
Задача 2.Найдите периметр прямоугольной трапеции, если известно нижнее основание AD = a, не перпендикулярная ему боковая сторона CD = d, а угол при этой боковой стороне ADC равен Альфа.Решение.Проведите высоту трапеции из вершины C на большее основание, получим отрезок CE, трапеция разделилась на две фигуры — прямоугольник ABCE и прямоугольный треугольник ECD. Гипотенуза треугольника — это известная нам боковая сторона трапеции CD, один из катетов равен перпендикулярной боковой стороне трапеции (по правилу прямоугольника две параллельные стороны равны — AB = CE), а другой — отрезок, длина которого равна разности оснований трапеции ED = AD — BC.

Найдите катеты треугольника: по существующим формулам CE = CD*sin(ADC) и ED = CD*cos(ADC).Теперь вычислите верхнее основание — BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа).Узнайте длину перпендикулярной боковой стороны — AB = CE = d*sin(Альфа).Итак, вы получили длины всех сторон прямоугольной трапеции.

Сложите полученные значения, это и будет периметр прямоугольной трапеции:P = AB + BC + CD + AD = d*sin(Альфа) + (a — d*cos(Альфа)) + d + a = 2*a + d*(sin(Альфа) — cos(Альфа) + 1).

Задача 3.Найдите периметр прямоугольной трапеции, если известны длины его оснований AD = a, BC = c, длина перпендикулярной боковой стороны AB = b и острый угол при другой боковой стороне ADC = Альфа.Решение.Проведите перпендикуляр CE, получите прямоугольник ABCE и треугольник CED.Теперь найдите длину гипотенузы треугольника CD = AB/sin(ADC) = b/sin(Альфа).Итак, вы получили длины всех сторон.

Сложите полученные значения:P = AB + BC + CD + AD = b + c + b/sin(Альфа) + a = a + b*(1+1/sin(Альфа) + с.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Трапеция – это такой четырехугольник, у которого 2 параллельных основания, а остальные стороны не параллельны друг другу. У прямоугольной трапеции один угол прямой, как вы уже наверняка догадались.

Шаг 1. Формула вычисления периметра прямоугольной трапеции

Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично. Тут она от остальных фигур ну ничем не отличается:

Шаг 2. Решение задач на тему определения периметра прямоугольной трапеции

Задача №1

Нужно найти периметр прямоугольной трапеции, когда даны длины всех сторон. Тут всё просто. Складываем все 4 значения, и готово. Это самый лёгкий вариант нахождения периметра. Остальные задачи в итоге всё равно сводятся к нему, но нужно рассмотреть и остальные варианты, интересно же!

Задача №2

Нужно найти периметр всё той же прямоугольной трапеции, но в этом случае мы знаем длину нижнего основания AD, которая равна a. Одна из боковых сторон CD, которая не перпендикулярна ему, равна d. Угол между этим основанием и стороной равен Альфа.

Решение задачи №2

Катеты находятся по таким формулам: CE = CD*sin(ADC), в свою очередь ED = CD*cos(ADC). Верхнее основание вычисляется так: BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа). Длина перпендикулярной стороны считается по формуле: AB = CE = d*sin(Альфа). После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.

Задача №3

Требуется найти периметр трапеции, когда даны длины его оснований. AD = a, BC=c. Также мы знаем длину перпендикулярной стороны AB, которая равна b. Острый угол при неперпендикулярной стороне равен Альфа.

Решение задачи №3

Для начала проведите высоту трапеции на большее основание, начало которой будет лежать в вершине С. После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник ABCE, а также треугольник ECD (прямоугольный). Гипотенузой треугольника в нашем случае будет известная нам сторона CD, один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.

Для начала снова проводим перпендикуляр CE и так же получаем прямоугольник ABCE вместе с треугольником CED. Осталось найти длину гипотенузы того треугольника, который мы получили, мы с уверенностью можем сказать, что CD = AB/sin(ADC) = b/sin(Альфа). Мы снова нашли все длины сторон. Осталось только их сложить. Надеемся, вы сможете сделать это без нас.

В данной публикации мы рассмотрим, каким образом можно посчитать периметр трапеции и разберем примеры решения задач.

Формула вычисления периметра

Периметр (P) трапеции равняется сумме длин всех ее сторон.

P = a + b + c + d

• b и d – основания трапеции;
• a и с – ее боковые стороны.

Периметр равнобедренной трапеции

В равнобедренной трапеции боковые стороны равны (a=c), из-за чего ее, также, называют равнобокой. Периметр считается так:

P =  2a + b + d или P = 2с + b + d

Периметр прямоугольной трапеции

Для расчета периметра используется такая же формула, что и для разносторонней трапеции.

P = a + b + c + d

Примеры задач

Задание 1
Найдите периметр трапеции, если ее основания равны 7 и 10 см, а боковые стороны – 4 и 5 см.

Решение:
Используем стандартную формулу, подставив в нее известные нам длины сторон: P = 7 см + 10 см + 4 см + 5 см = 26 см.

Задание 2
Периметр равнобедренной трапеции равняется 22 см. Найдите длину боковой стороны, если основания фигуры равны 3 см и 9 см.

Решение:
Как мы знаем, периметр равнобедренной трапеции вычисляется по формуле: P = 2a + b + d, где а – боковая сторона.
Ее длина, умноженная на два равна: 2a = P – b – d = 22 см – 3 см – 9 см = 10 см.
Следовательно, длина боковой стороны составляет: a = 10 см / 2 = 5 см.

Как найти площадь и периметр равнобедренной трапеции? Как найти площадь и периметр прямоугольной трапеции? Площадь трапеции, у которой основания a1 и a2, средняя линия m = (a1 + a2)/2, а высота h. S = (a1 + a2)*h/2 = m*h Периметр равнобочной трапеции, у которой боковые стороны равны b P = a1 + a2 + 2*b У прямоугольной трапеции одна боковая сторона перпендикулярна основаниям, то есть совпадает с высотой. Вторая равна b. P = a1 + a2 + h + b автор вопроса выбрал этот ответ лучшим Stasy­12 [41.5K] 5 лет назад  Геометрия интересная наука, другое дело, что не каждому она дается на изучение. Пыталась «дружить» с геометрией, конечно, не всегда все было гладко, но, если по формулам, то все удавалось. Доказывать теоремы нравилось. Так вот трапеция, помню из курса геометрии это фигура, которая имеет разные длины сторон.Поэтому эти стороны обычно обозначают разными буквами латинского алфавита. Чтобы вычислить периметр необходимо все стороны просто сложить Чтобы получить площадь трапеции руководствуйтесь вот этой формулой: Вывести формулу площади трапеции можно самостоятельно, если вспомнить, что трапеция — это прямоугольник у которого одна или две стороны скошены. Площадь прямоугольника находится по формуле 1/2 ав, где а и в — стороны прямоугольника. Но точно та же формула будет справедлива и для трапеции, только если сторона В в трапеции будет равна ее высоте, то сторона А окажется равной средней линии трапеции. А средняя линия трапеции находится по формуле (А+Б)/2. Тогда получаем, что площадь трапеции следует искать по форомуле: S = (A+B)/2*H Ну а периметр трапеции находится как сумма всех его сторон. Если боковые стороны не известны, то пригодится теорема Пифагора как для равнобедренной трапеции, так и для прямоугольной. Ксарф­акс [156K] 6 лет назад  Периметр трапеции Как известно, трапеция имеет четыре стороны. Периметр — это сумма длин всех сторон, в случае с обычной или прямоугольной трапецией он будет равен: P = AD + CD + BC + AB. Если трапеция равнобедренная, то AD = BC. Соответственно, P = 2AD + CD + AB. Площадь трапеции В общем случае она определяется по следующей формуле: S = h*(AB + CD)/2, где h — высота, проведённая к основанию AB и (AB + CD)/2 — средняя линия трапеции. В случае с прямоугольной трапецией её высота совпадает с одной из боковых сторон. Формула будет той же, но теперь вместо высоты трапеции будет фигурировать её сторона: S = AD*(AB + CD)/2 Авато­рия [71K] 5 лет назад  Площадь трапеции можно найти несколькими способами, все зависит от того, какие данные уже есть. Для этого есть формулы нахождения площади трапеции. Через основание и высоту: Через высоту и среднюю линию: Через все четыре стороны: Через диагонали и угол между ними: Через радиус вписанной окружности и угол: Ну а периметр любой фигуры ищется сложением сумм всех сторон: Любоп­ытств­о [135K] 5 лет назад  Что представляет собой трапеция? Прямоугольник со скошенными сторонами. Если это помнить, площадь прямоугольника со сторонами а и в можно искать по следующей формуле: 1:2 ав. А в трапеции в — ее высота, А равна средней линии трапеции (А+Б):2. Таким образом, нам нужна вот эта формула площади: S = (A+B)/2*H Периметр же ищем по теореме Пифагора. Galin­a7v7 [120K] 7 лет назад  Равнобедренная трапеция: Пусть известны основания трапеции a и b (a > b) , и боковые стороны c = d. Периметр Р = a + b + 2c Площадь : S= [(a+b)2]*h , где h — высота трапеции. Найдём h: h = √[c^2 — (a — b)^2/4]. Для прямоугольной трапеции: a , b — основания , h — высота и боковая сторона , с — 2-я боковая сторона. Периметр Р = a + b + c + h , но h = √ [c^2-(a-b)^2] Площадь S = [(a + b)/2}*h = [(a + b)/2]*√ [c^2 — (a — b )^2]. При других исходных данных (например , углы при основании ) формулы периметра и площади будут немного другие. Алиса в Стран­е [364K] 5 лет назад  Начнем по порядку, с более простого, — с определения периметра трапеции. Допустим, у нас трапеция с вершинами А, В, С, D. Тогда периметр нашей трапеции равен длине всех ее сторон: Р = АВ + ВС + СD + DА. Так, с периметром трапеции разобрались, ничего сложного в этом нет. Теперь площадь трапеции. Для площади трапеции применяем специальную формулу: Пропо­ведни­к [97.1K] 7 лет назад  Ну это смотря что известно об этой трапеции. Проще всего площадь трапеции найти так: высота умножить на длину короткой стороны прибавить отношение произведения высоты на разность длинной и короткой сторон к двум. Стороны, которые имеются ввиду- это те, которые паралленые друг другу, основания трапеции. vksvo­vko [1.6K] 6 лет назад  Чтобы найти периметр трапеции нужно сложить все его стороны. Чтобы найти площадь необходимо сложить 2 основания, поделить на два и умножить на высоту. Чтобы вычислить периметр часто в задачах нужно с начала подсчитать площадь а далее найти ребра. Знаете ответ?

Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной

Принятые в формулах обозначения

Во всех приведенных ниже математических записях верны такие прочтения букв.

произвольная трапеция	равнобедренная трапеция	название
а	а	нижнее основание
в	в	верхнее основание
с, d	с	боковые стороны
н	н	высота
m	m	средняя линия
d1, d2	d1	диагонали
s	s	площадь
α, β	α	углы при нижнем основании
γ, δ	γ, δ	углы на пересечении диагоналей

Найти периметр трапеции

Введите данные:

Вводить можно числа или дроби (-2.4, 5/7, …).

Основные свойства равнобедренной трапеции

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:

Формулы длин сторон равнобедренной трапеции:

a = b + 2 h ctg α = b + 2 c cos α

b = a – 2 h ctg α = a – 2 c cos α

c =	h	=	a – b
sin α	2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d 1 2 – c 2	b =	d 1 2 – c 2	c = √ d 1 2 – ab
b	a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	– b b =	2S	– a
h	h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

Формулы длины средней линии равнобедренной трапеции:

m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2

2. Формула средней линии трапеции через площадь и сторону:

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√ 4 c 2 – ( a – b ) 2
2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a – b	tg β	= c sin β
2

В исходных данных: все стороны

Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:

н = √(с 2 – (((а – в) 2 + с 2 – d 2 )/(2(а – в))) 2 ). Номер 1.

Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.

Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:

н = √(с 2 – (а – в) 2 /4). Номер 2.

Периметр произвольной трапеции

Периметр произвольной трапеции, в которой AB=a , BC=b , CD=c , AD=d , имеет вид:

[ LARGE P_ = a + b + c + d ]

где:
P – периметр трапеции
a, b, c, d – стороны трапеции

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и она делит боковую сторону точкой касания на два отрезка — и , то , то

Решение задач о прямоугольной трапеции

Прямоугольной называют трапецию, у которой углы при одной из боковых сторон равны 90 0 . Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.

Задача Даны три стороны, одна из которых перпендикулярная боковая.

Допустим, нам дана прямоугольная трапеция АВСД, у которой АВ перпендикулярно ВС. Известно, что АВ = 12 см, ВС = 1 см, АД = 6 см. Необходимо найти большую боковую сторону.

Из точки С опускаем проводим высоту СК и получаем прямоугольный треугольник СДК и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны СК = АВ = 12 см, а АК = ВС = 1 см.

Находим отрезок КД:

• КД = АД – АК = 6 – 1 = 5 (см)

Согласно теореме Пифагора:

• СД 2 =СК 2 +КД 2 =12 2 +5 2 =144+25=169
• СД = √169 = 13 (см)

Ответ: СД = 13 см

Задача Даны оба основания и угол при основании

Дана трапеция АВСД, у которой основания ВС и АД равны 6 и 10 см соответственно, угол ВАД – прямой, а СДА равен 45 градусов. Найдите меньшую боковую сторону.

1. Проводим высоту СК и получаем прямоугольный треугольник СКД и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.
2. КД = АД – АК = 10 – 6 = 4 см
3. cos 45 = √2/2 = КД / СД, отсюда СД = КД / cos 45
4. Получаем СД = 4/√2/2 = 4√2 (см)

Ответ: СД = 4√2 см

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Определение периметра прямоугольной трапеции

Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:

Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.

• опустим высоту из вершины С, высота CH = AB = 5см;
• исходя из рисунка 3, AH = BC = 7 см;
• HD = AD – AH = 10 – 7 = 3 см;
• далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
• подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:

• формула расчета длины основания через среднюю линию;
• формулы длин сторон через высоту и угол при нижнем основании трапеции;
• формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
• формулы длин сторон равнобедренной трапеции через площадь.

Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.

Известны: диагонали и углы между ними

Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:

Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:

н = (d₁ 2 * sin γ) / (а + в) или н = (d₁ 2 * sin δ) / (а + в). Номер 6.

Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:

н = (d₁ 2 * sin γ) / 2m или н = (d₁ 2 * sin δ) / 2m. Номер 6а.

Трапеция. Формулы, признаки и свойства трапеции

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

• Основы трапеции — параллельные стороны
• Боковые стороны — две другие стороны
• Средняя линия — отрезок, соединяющий середины боковых сторон.

• Равнобедренная трапеция — трапеция, у которой боковые стороны равны
• Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

BC : AD = OC : AO = OB : DO

d ₁ 2 + d ₂ 2 = 2 a b + c 2 + d 2

Сторона трапеции

Формулы определения длин сторон трапеции:

a = b + h · ( ctg α + ctg β )

b = a — h · ( ctg α + ctg β )

a = b + c· cos α + d· cos β

b = a — c· cos α — d· cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

h = c· sin α = d· sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d 1 d 2	=	sin δ ·	d 1 d 2
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d 1 d 2	=	sin δ ·	d 1 d 2
2 m	2 m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

d ₁ = √ a 2 + d 2 — 2 ad· cos β

d ₂ = √ a 2 + c 2 — 2 ac· cos β

2. Формулы диагоналей через четыре стороны:

d 1 =	√	d 2 + ab —	a ( d 2 — c 2 )
a — b

d 2 =	√	c 2 + ab —	a ( c 2 — d 2 )
a — b

d ₁ = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2

d ₂ = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2

d ₁ = √ c 2 + d 2 + 2 ab — d ₂ 2

d ₂ = √ c 2 + d 2 + 2 ab — d ₁ 2

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

3. Формула площади через диагонали и угол между ними:

S =	d 1 d 2	· sin γ	=	d 1 d 2	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c 2 —	(	( a — b ) 2 + c 2 — d 2	)	2
2	2( a — b )

5. Формула Герона для трапеции

S =	a + b	√ ( p — a )( p — b )( p — a — c )( p — a — d )
| a — b |

где

p =	a + b + c + d	— полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d 1
4√ p ( p — a )( p — c )( p — d 1)

где

a — большее основание

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как найти периметр прямоугольной трапеции вписанной окружности

Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 42. Найдите радиус окружности.

В четырехугольник можно вписать окружность тогда и только тогда, когда

Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.

Пусть радиус вписанной окружности равен r, тогда длина меньшей боковой стороны равна 2r. Суммы длин противоположных сторон описанного вокруг окружности четырехугольника равны, поэтому сумма оснований трапеции равна сумме длин ее боковых сторон или 2r + 9. Тогда для периметра трапеции имеем 2(2r + 9) = 32, откуда r = 3,5.