Задания
Версия для печати и копирования в MS Word
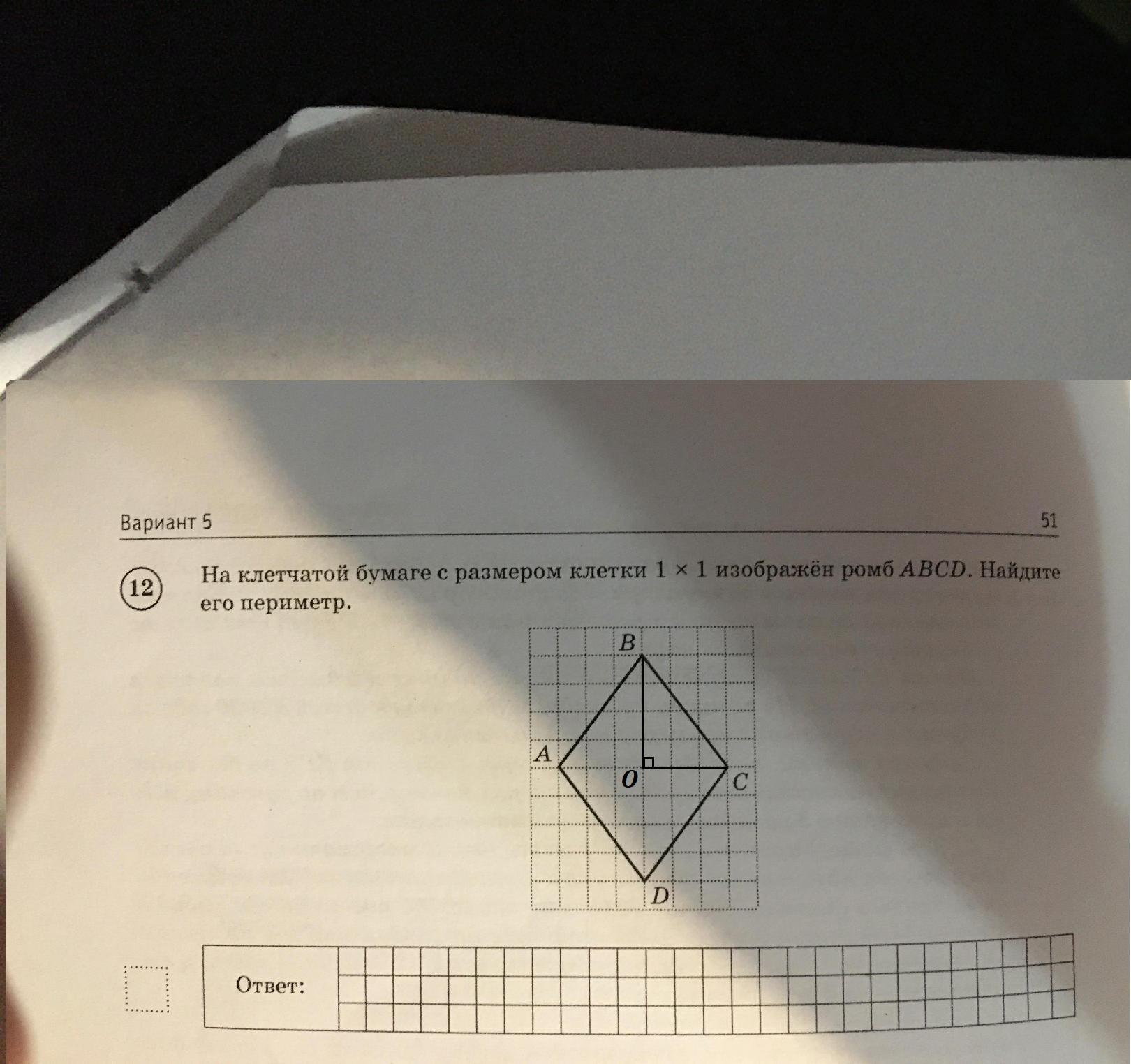
На клетчатой бумаге с размером клетки 1 × 1 изображён ромб ABCD. Найдите его периметр.
Спрятать решение
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из рисунка видно, что диагонали AC и BD равны 8 и 6 соответственно. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдём сторону ромба: Так как все стороны ромба равны, то периметр равен:
Ответ: 20.
Условно проведем диагонали ромба ABCD, которые делятся точкой пересечения пополам и образуют между собой угол 90°
АС = 6 см
ВD = 8 см
Тогда АО = 3 см и ВО = 4 см, а значит, из ΔАОВ по теореме Пифагора (или по правилу египетского треугольника):
АВ = √9+16 = √25 = 5 см
*По египетскому треугольнику если катеты равны 3 и 4 см, то гипотенуза равна 5 см*
Периметр ромба равен 4а , т.к. все его стороны равны
Р = 4*5 = 20 см
Ответ: 20 см
Ответ:
20
Пошаговое объяснение:
- Ромб — параллелограмм, у которого все стороны равны.
⇒ AB = BC = CD = AD
Внутри данного ромба построим прямоугольный ΔBOC, где BC — гипотенуза.
Так как 1 клетка = 1 ⇒ OC = 3 (так как 3 клетки) и BO = 4 (так как 4 клетки)
В ΔBOC:
Найдём BC по теореме Пифагора:
⇒ AB = BC = CD = AD = 5
- Периметр фигуры — сумма всех её сторон.
⇒
Или:
Так как в ромбе все стороны равны и этих сторон всего 4, то:
Приложения:
Решение:
На рисунке изображен ромб, а у ромба все стороны равны, значит, достаточно найти длину только одной его стороны.
Сделаем дополнительное построение таким образом, чтобы какая-нибудь из сторон стала гипотенузой прямоугольного треугольника.
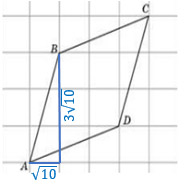
Если длина одной клетки равна √10, тогда один из катетов будет равен 3√10, а другой — √10.
По теореме Пифагора найдем АВ:
А теперь найдем периметр)
Ответ: 40.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#796
Условие
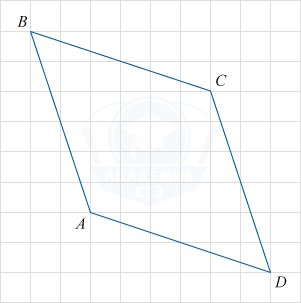
На клетчатой бумаге с размером клетки sqrt{10}timessqrt{10} изображен четырехугольник ABCD. Найдите его периметр.
Показать решение
Решение
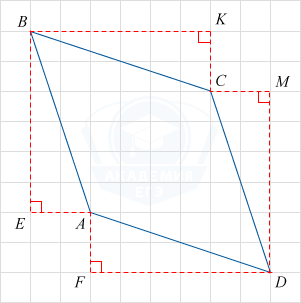
triangle BKC = triangle MDC = triangle AFD = triangle ABE по двум катетам, следовательно BC=CD=AB=AD, откуда следует, что ABCD — ромб.
BK=6sqrt{10}, KC=2sqrt{10}, BC=sqrt{BK^2+KC^2}=sqrt{(6sqrt{10})^2+(2sqrt{10})^2}=20.
Пусть P_{ABCD} — периметр ромба ABCD.
P_{ABCD} = 4cdot BC=4cdot20=80.
Ответ
80
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.