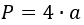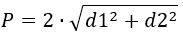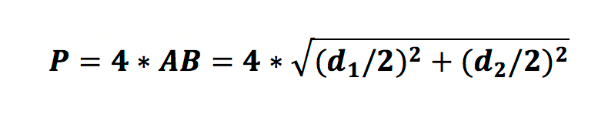Как найти периметр ромба не зная сторон - Исправление недочетов и поиск решений вместе с Examum.ru

Download Article

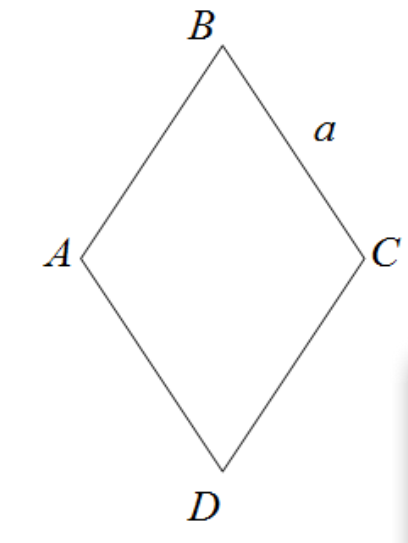
A rhombus is a parallelogram with four congruent sides.^[1] These properties allow for numerous methods for finding the perimeter. Since all four sides of a rhombus are of equal length, finding the perimeter is possible when one side length is known. However, using geometry and trigonometry, it is also possible to find the perimeter even if you do not know the lengths of any sides of the rhombus.

1
Set up the formula for perimeter of a rhombus. Since, by definition, all four sides of a rhombus are the same length, the formula is , where equals the perimeter, and equals the length of one side.^[2]
- You could also use the formula to find the perimeter, since the perimeter of any polygon is the sum of all its sides.^[3]
- If you know that not all sides are the same length, then you are not working with a rhombus, and you cannot use this formula.
- If you don’t know the length of any side of the rhombus, you cannot use this method.
- A square is a special type of rhombus, with four 90-degree angles.
2
Plug in the side length of the rhombus. Make sure you are substituting for the variable .
- For example, if you know one side of the rhombus is 4 meters long, your formula will look like this: .
Advertisement
3

Solve for . To do this, multiply by 4.

1
Notice that the two diagonals of your rhombus create four congruent triangles. Outline one of these triangles. You will use it to find the length of one side of the rhombus.
- Since the triangles are congruent, it doesn’t matter which one you outline.
2

Identify the 90 degree angle of your triangle. The two diagonals of a rhombus are perpendicular, so the central angle of your triangle will be 90 degrees. ^[4]
3
Label the hypotenuse of your triangle. The hypotenuse is the side opposite a 90 degree angle.^[5]Traditionally, the hypotenuse is labeled .
- The hypotenuse of your triangle is one side of the rhombus. So, if you find the length of , you will know the length of one side of the rhombus.
4

Label the other two sides of your triangle. Traditionally, these are labeled and .
5

Find the length of side . To do this, divide the length of the diagonal that runs along by 2. Label the side length on your triangle.
6

Find the length of side . To do this, divide the length of the diagonal that runs along by 2. Label the side length on your triangle.
7

Set up the Pythagorean Theorem. The theorem states that $a^{{2}}+b^{{2}}=c^{{2}}$ . This is a basic geometric formula for finding the side lengths of a right triangle.
8

Plug in the known side lengths of your triangle into the Pythagorean Theorem. Make sure you substitute for and , but the order doesn’t matter due to the commutative property.
9
10
11
Write your final answer. Don’t forget to include the correct unit of measurement.
- For example, a rhombus that has diagonals measuring 12 and 16 meters long has a perimeter of 40 meters.

1

Label the vertices of your rhombus, if they are not already labeled. It doesn’t matter which variables you give them.
2
Notice that the two diagonals of your rhombus create four congruent triangles. Outline one of these triangles. You will use it to find the length of one side of the rhombus.
- Since the triangles are congruent, it doesn’t matter which one you outline; however, for simplicity you should outline a triangle that shares a known angle of the rhombus.
- For example, I know that angle of the rhombus is 70 degrees, so I would outline a triangle that includes point A.
3

Identify the 90 degree angle of your triangle. The two diagonals of a rhombus are perpendicular, so the central angle of your triangle will be 90 degrees. ^[7]If this angle is not already labeled, label it .
4
5

Determine the measurement of the missing angle. Remember, the interior degrees of a triangle will add up to 180.^[9] So, if you know the measurement of two angles, you can subtract to find the measurement of the third angle. Label the degrees for this angle on your triangle.
6

Determine the length of one side of your triangle. To do this, divide the length of the diagonal that the side runs along by 2. Label the side length on your triangle.
7
Set up a sine or cosine ratio. Whether you use sine or cosine will depend on which side and angle measurements of your triangle you know. For more information, read Use Right Angled Trigonometry.
- If you know the length of the side opposite to your angle, use sine. Set up the ratio $sin(theta )={frac {Opposite}{h}}$ , where is the measurement of the angle, “Opposite” is the length of the opposite side, and is the length of the hypotenuse.
- If you know the length of the side adjacent to your angle, use cosine. Set up the ratio $cos(theta )={frac {Adjacent}{h}}$ . Where is the measurement of the angle, “Adjacent” is the length of the adjacent side, and is the length of the hypotenuse.
- For example, if you know that angle of your triangle is 35 degrees, and the adjacent side is 8 centimeters, you should use cosine:
  $cos(35)={frac {8}{h}}$
8

Solve the ratio to find the length of the hypotenuse. The length of the hypotenuse is also the length of one side of your rhombus, so you need this measurement to find the perimeter of the rhombus.
9
10

Write your final answer. Your answer will be approximate since you rounded the sine or cosine measurement. Don’t forget to include the correct unit of measurement.

Add New Question

Question

What is the perimeter and area of a rhombus with diagonals of 24 cm and 7 cm?

To find the perimeter, follow the steps described in method 2, where you use the lengths of the diagonals to set up the Pythagorean Theorem.
1/2 of 24 = 12; 1/2 of 7 = 3.5.
So:
12^2 + 3.5^2 = c^2
144 + 12.25 = c^2
156.25 = c^2
12.5 = c, or the length of one side of the rhombus (S)
P = 4S
P = 4(12.5)
P= 50 cm

To find the area, you can read the article «Calculate the Area of a Rhombus.» (http://www.wikihow.com/Calculate-the-Area-of-a-Rhombus)
Question

What if the sides are not equal?

If the sides of the shape are not equal, then the figure is not a rhombus. You can still find the perimeter of any shape by adding up the length of all its sides.
Question

How do I find the perimeter of a rhombus whose area is 60 cm2 and has a diagonal of 15 cm?

The area (60) is half the product of the diagonals. If d is the unknown diagonal, then 60 = 15d / 2. So 15d = 120, and d = 8 cm. The diagonals of a rhombus are perpendicular to and bisect each other, forming four right triangles, each with legs of 7.5 cm and 4 cm (half each diagonal). By the Pythagorean theorem, we find that each of the sides of the rhombus is √([7.5)² + (4)²] = √[56.25 + 16] = √72.25 = 8.5 cm. The perimeter of the rhombus is four times the length of one side: 34 cm.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

You can add up the lengths of the sides to get the perimeter of any polygon – a triangle, rectangle, pentagon, or other straight-sided shape. Circles and other curved shapes require different formulas.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To find the perimeter of a rhombus when you have the length of one of the sides, multiply that length by 4. This works because all 4 sides of a rhombus are equal length. Keep reading to learn how to use the Pythagorean Theorem to find the perimeter of a rhombus when you know the diagonal!

Did this summary help you?

Thanks to all authors for creating a page that has been read 102,847 times.

Did this article help you?

Источник

В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.

Формула вычисления периметра
Примеры задач

Формула вычисления периметра

1. По длине стороны

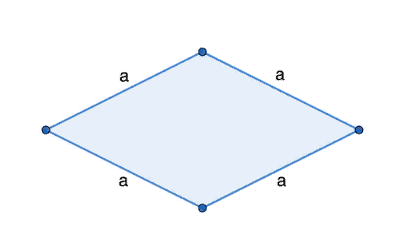
Периметр (P) ромба равняется сумме длин всех его сторон.

P = a + a + a + a

Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):

P = 4*a

2. По длине диагоналей

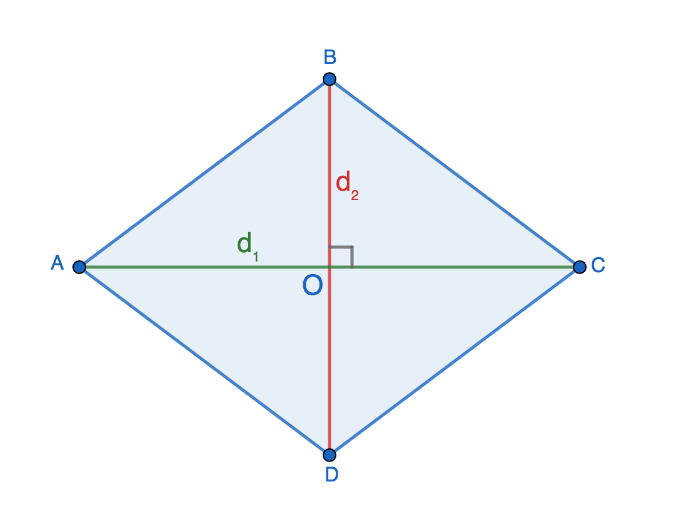
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:

AO=OC=d₁/2
BO=OD=d₂/2

Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.

Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:

AB² = AO² + OB²

Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:

AB² = (d₁/2)² + (d₂/2)², или

Таким образом, периметр равняется:

Примеры задач

Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.

Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.

Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.

Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.

Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.

Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:

Источник

Периметр ромба калькулятор онлайн умеет вычислять периметр двумя способами:

По стороне ромба.
По диагоналям ромба.

Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.

Периметр ромба- это сумма всех его сторон.
Так как у ромба все стороны равны, то периметр равен длине любой его стороны, умноженной на четыре.

Как найти периметр ромба?

Найти периметр ромба очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

1) По стороне ромба

где a- любая из равных сторон ромба.

2) По двум диагонялям

где d1,d2 — диагонали ромба.

Скачать все формулы в формате Word

Источник

Что нужно знать о периметре ромба — основные сведения

Содержание:

Основные сведения о фигуре ромб
- Понятие периметра ромба
Способы нахождения периметра
- Через стороны
- Через длину диагонали
Формулы для каждого способа
Примеры решения задач

Источник: microexcel.ru

Основные сведения о фигуре ромб

Рассмотрим особый вид параллелограмма, для которого характерны следующие признаки:

Две стороны, являющиеся смежными, равны по величине.
Проведенные из углов диагонали пересекаются в центре фигуры таким образом, что образуют прямой угол.
Определенная диагональ разделяет углы, которые она соединяет, пополам.

По этим признакам можно четко определить, когда параллелограмм является ромбом.

Ромбом называется геометрическая фигура, которая является параллелограммом и имеет все четыре стороны равной длины.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Произошло название от греческого слова ῥόμβος либо латинского rombus. В переводе они означают «бубен».

При этом геометрическими свойствами ромба являются:

Поскольку ромб — параллелограмм, его стороны, лежащие противоположно, имеют равные величины и попарную параллельность. Кроме этого, для всех ромбов характерно равенство противоположных углов, а также факт, что соседние с ними углы составляют в сумме 180о.
С помощью проведения диагоналей можно разделить ромб на четыре треугольника, имеющих прямые углы. При этом диагонали пересекутся в центре фигуры в точке, которая разделит их пополам.
Вышеуказанные диагонали будут биссектрисами углов ромба.
Если длину диагоналей возвести в квадрат и сложить эти квадраты, то получишь квадрат стороны, увеличенный в 4 раза (данное свойство вытекает из тождества параллелограмма).
В ромб можно вписать прямоугольник, при этом его углы будут располагаться на серединах его сторон.
Оси симметрии ромба обязательно будут перпендикулярны диагоналям ромба.
Кроме прямоугольника в ромб можно вписать окружность. Ее центр будет совпадать с точкой, в которой пересекаются диагонали.

Зная вышеизложенные свойства, легко проводить вычисления величин, характеризующих данный ромб и строить внутри него геометрические фигуры.

Понятие периметра ромба

Периметр любой плоской геометрической фигуры составляет сумму длин его границ. Ромб не является исключением.

Исходя из определения, единицы измерения периметра аналогичны единицам длины.

Однако найти периметр ромба можно не только сложив длины всех четырех сторон. В геометрии существует еще один метод, который детально будет рассмотрен ниже.

Способы нахождения периметра

Через стороны

Поскольку у ромба все четыре стороны равны, его периметр можно выразить произведением длины одной стороны на 4.

P=4a

где P — периметр, a — длина стороны.

Источник: ru.solverbook.com

Нахождение периметра ромба можно проводить по еще одной формуле, используя длины диагоналей.

Через длину диагонали

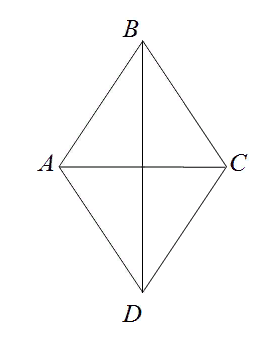
Рассмотрим рисунок.

Источник: microexcel.ru

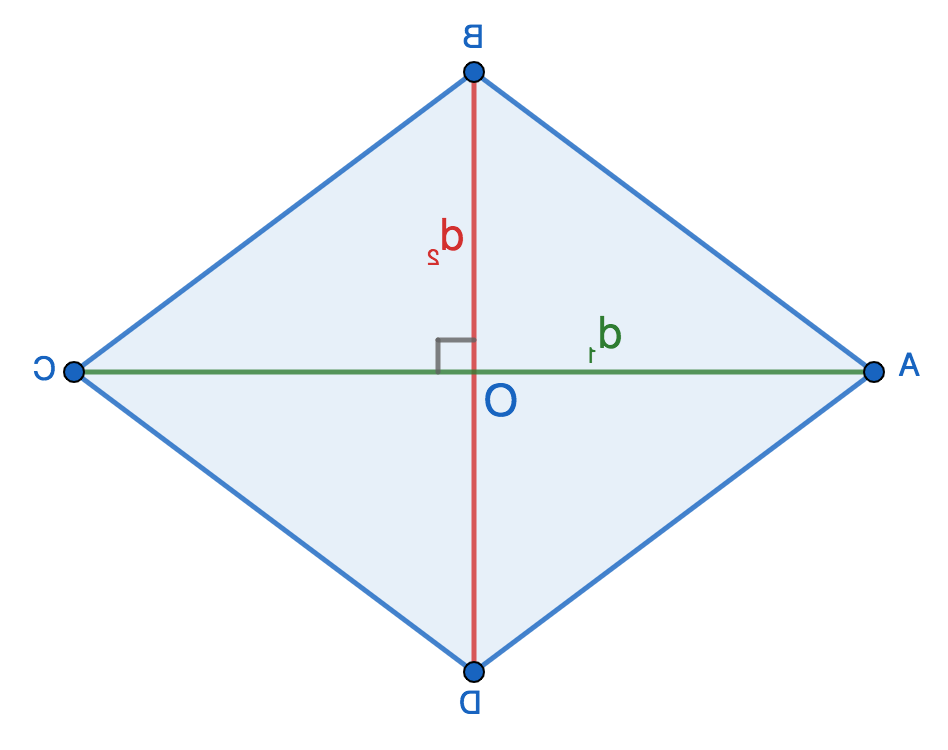
Проведем в ромбе ABCD диагонали BD и AC. Они пересекаются в точке O под прямым углом и делятся этой точкой пополам. Можно записать равенства:

AO=OC=d1/2

BO=OD=d2/2

В результате деления ромба диагоналями на четыре треугольника, имеющих прямые углы, образовались геометрические фигуры AOB, AOD, BOC, DOC. Подробнее рассмотрим один треугольник — AOB.

Из рисунка видно, что сторона AB являясь стороной ромба, представляет собой гипотенузу в прямоугольнике. Далее воспользуемся известной теоремой Пифагора:

AB²=AO²+OB²

В эту формулу подставим величины длин катетов. Однако перед этим выразим их через ½ диагоналей.

AB²=(d₁/2)²+(d₂/2)²

Извлекая квадрат из этого выражения, получаем:

AB=√((d₁/2)²+(d₂/2)²)

В итоге находим периметр ромба:

Источник: microexcel.ru

Формулы для каждого способа

В ходе решения задач по теме «ромб» применяются следующие формулы:

Для нахождения периметра:

Через длину стороны: P=4a

Источник: microexcel.ru

Используя длины диагоналей:

Источник: calculators.vip

Кроме этого, на уроках по изучению характеристик ромба, рассматриваются формулы по нахождению его площади. Ее можно определить с помощью двух способов: через вычисление произведения высоты на длину стороны или половину произведения двух диагоналей.

Источник: www.webmath.ru

Примеры решения задач

Задача 1

Длина стороны ромба составляет 10 см. Чему равен его периметр?

Решение.

Находить следует с использованием формулы: P=4a. Подставляем значение длины стороны и получаем P=40 см

Задача 2

Периметр ромба равен 36 см. Чему равна длина его стороны?

Решение.

Используется формула для нахождения периметра. Из нее вытекает действие для нахождения длины стороны: a=P/4

a=36/4=9 см

Задача 3

Дан ромб с длинами диагоналей 8 и 6 см. Чему равен его периметр?

Решение.

Используем способ нахождения периметра через квадрат из суммы квадратов половины диагоналей:

P=4*√((8/2)²+(6/2)²⁾=20см

Задача 4

Известно, что в ромбе одна из диагоналей равна 6 см, а один из углов равен 60о. Каков периметр этого ромба?

Решение.

Источник: ru.solverbook.com

Предположим, что длина диагонали AC составляет 6 см, а угол ABC составляет 60^о

Обозначим длину стороны ромба (а по определению длины всех сторон равны) буквой a.

По основному свойству ромба о равенстве длин его сторон, треугольник ABC равнобедренный. В то же время, поскольку один из его углов равен 60^о, он еще и равносторонний.

a=AC=6см

Теперь применяем формулу для нахождения периметра ромба через длину стороны:

P_ABCD=4*6=24 см

Источник

Периметр ромба

Ромб — это четырехугольник с равными сторонами.

Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.

Периметр ромба — сумма длин всего его сторон или произведение любой его стороны на 4.

Способы нахождения

Рассмотрим все способы нахождения периметра этой фигуры.

По сторонам

Периметр ромба по сторонам

Источник: microexcel.ru

Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:

(P;=;a+a+a+a;=;4times a,)

где a — это сторона ромба.

По двум диагоналям

Периметр ромба по двум диагоналям

Источник: microexcel.ru

Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:

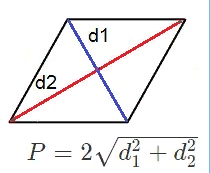
(P=4timessqrt{left(d_1/2right)^2+left(d_2/2right)^2},)

где (d_1) и (d_2) — это диагонали четырехугольника.

Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:

(a^2=left(d_1/2right)^2+left(d_2/2right)^2)

(a=sqrt{left(d_1/2right)^2+left(d_2/2right)^2}.)

По диагонали и углу

Периметр ромба по диагоналям и углу

Источник: math24.ru

Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:

если нам известен острый угол α: (a=frac{d_1}{sqrt{2+2cosalpha}};)
если известен тупой угол (β: a=frac{d_2}{sqrt{2-2cosbeta}}.)

Далее расчет P будет выглядеть следующим образом:

(P=frac{4d_1}{sqrt{2+2cosalpha}});
(P=frac{4d_2}{sqrt{2-2cosbeta}}.)

По площади и радиусу вписанной окружности

Периметр ромба по площади и радиусу вписанной окружности

Источник: ru.solverbook.com

По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:

(P=frac{2S}r,)

где r — это радиус вписанной окружности.

По площади и синусу одного из углов

В этом случае формула расчета суммы всех сторон выглядит так:

(P=4timesfrac{sqrt S}{sqrt{sinalpha}},) либо

(P=4timesfrac{sqrt S}{sqrt{sinbeta}}.)

Через большую диагональ и половинный угол

Периметр ромба через большую диагональ и половинный угол

Источник: math24.ru

(P=frac{2d_1}{sqrt{cos(alpha/2)}}) или

(P=frac{2d_1}{sqrt{sin(beta/2)}}.)

Источник

Video

References

About This Article

Did this article help you?

Формула вычисления периметра

<img fetchpriority="high" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://microexcel.ru/wp-content/uploads/2020/03/perimetr-romba-1.png" alt="Периметр ромба" width="350" height="189" />

Примеры задач

Как найти периметр ромба?

1) По стороне ромба

2) По двум диагонялям

Скачать все формулы в формате Word

Что нужно знать о периметре ромба — основные сведения

Основные сведения о фигуре ромб

Понятие периметра ромба

Способы нахождения периметра

Через стороны

Через длину диагонали

Формулы для каждого способа

Примеры решения задач

Периметр ромба

Способы нахождения

По сторонам

По двум диагоналям

По диагонали и углу

По площади и радиусу вписанной окружности

По площади и синусу одного из углов

Через большую диагональ и половинный угол