Как найти периметр треугольника 5класс - Исправление недочетов и поиск решений вместе с Examum.ru

Выбирайте формулу в зависимости от известных величин.

1. Как найти периметр треугольника, зная три стороны

Просто посчитайте сумму всех сторон.

Иллюстрация: Лайфхакер

P — искомый периметр;
a, b, c — стороны треугольника.

2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности

Умножьте площадь треугольника на 2.

Разделите результат на радиус вписанной окружности.

Иллюстрация: Лайфхакер

P — искомый периметр;
S — площадь треугольника;
r — радиус вписанной окружности.

3. Как вычислить периметр треугольника, зная две стороны и угол между ними

Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:

Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
Найдите корень из результата.

Теперь прибавьте к найденной стороне две ранее известные стороны.

Иллюстрация: Лайфхакер

P — искомый периметр;
b, c — известные стороны треугольника;
ɑ — угол между известными сторонами;
a — неизвестная сторона треугольника.

4. Как найти периметр равностороннего треугольника, зная одну сторону

Умножьте сторону на 3.

Иллюстрация: Лайфхакер

P — искомый периметр;
a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).

5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание

Умножьте боковую сторону на 2.

Прибавьте к результату основание.

Иллюстрация: Лайфхакер

P — искомый периметр;
a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
b — основание треугольника (это сторона, которая отличается длиной от остальных).

6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту

Найдите квадраты боковой стороны и высоты.

Отнимите от первого числа второе.

Найдите корень из результата и умножьте его на 2.

Прибавьте к полученному числу две боковые стороны.

Иллюстрация: Лайфхакер

P — искомый периметр;
a — боковая сторона треугольника;
h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).

7. Как вычислить периметр прямоугольного треугольника, зная катеты

Найдите квадраты катетов и посчитайте их сумму.

Извлеките корень из полученного числа.

Прибавьте к результату оба катета.

Иллюстрация: Лайфхакер

P — искомый периметр;
a, b — катеты треугольника (стороны, которые образуют прямой угол).

8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу

Посчитайте квадраты гипотенузы и катета.

Отнимите от первого числа второе.

Найдите корень из результата.

Прибавьте катет и гипотенузу.

Иллюстрация: Лайфхакер

P — искомый периметр;
a — любой катет прямоугольника;
c — гипотенуза (сторона, которая лежит напротив прямого угла).

Источник

Загрузить PDF

Периметр треугольника — это общая длина всех его сторон.^[1] Самый простой способ найти периметр треугольника заключается в том, чтобы сложить длины всех его сторон, однако если вы не знаете длину хотя бы одной стороны треугольника, необходимо сначала найти ее. В первом разделе данной статьи рассказано, как вычислить периметр треугольника по трем известным сторонам — это наиболее простой и распространенный метод. Затем показано, как найти периметр прямоугольного треугольника, если известны длины двух сторон. И наконец, описано, как с помощью теоремы косинусов рассчитать периметр любого треугольника, если даны две стороны и угол между ними.

1
Запомните формулу, которая позволяет вычислить периметр треугольника. Если треугольник имеет стороны a, b и c, его периметр P равен: P = a + b + c.
- Таким образом, чтобы найти периметр треугольника, следует сложить длины всех трех его сторон.
2
Посмотрите на треугольник и узнайте длины всех трех сторон. Предположим, треугольник имеет следующие стороны: a = 5, b = 5 и c = 5.
- Рассматриваемый треугольник называется равносторонним, так как все три его стороны имеют одинаковую длину. Тем не менее формула для расчета периметра справедлива для любого треугольника.
3
Сложите длины всех трех сторон, чтобы найти периметр. В нашем примере 5 + 5 + 5 = 15, то есть P = 15.
- Рассмотрим другой пример: a = 4, b = 3 и c=5. В этом случае периметр равен: P = 3 + 4 + 5 = 12.
4
В ответе не забывайте указывать единицу измерения. Если стороны измеряются в сантиметрах, окончательный ответ также должен быть приведен в сантиметрах. Ответ должен быть в тех же единицах, в которых приведены длины сторон в условии задачи.
- В приведенном примере длина каждой стороны составляет 5 сантиметров, поэтому периметр равен 15 сантиметрам.
Реклама

1

Запомните, что такое прямоугольный треугольник. Прямоугольным называется такой треугольник, один из углов которого является прямым, то есть равен 90 градусам. Самая длинная сторона такого треугольника всегда лежит напротив прямого угла и называется гипотенузой. Две другие стороны, образующие прямой угол, называются катетами. Прямоугольные треугольники очень часто встречаются в задачах по математике. К счастью, есть формула, с помощью которой всегда можно рассчитать длину неизвестной стороны!
2

Вспомните теорему Пифагора. Эта теорема гласит, что в любом прямоугольном треугольнике с катетами a и b и гипотенузой c стороны связаны следующим соотношением: a² + b² = c².^[2]
3

Нарисуйте прямоугольный треугольник и обозначьте стороны как a, b и c. Самая длинная сторона прямоугольного треугольника — это гипотенуза. Она лежит напротив прямого угла. Обозначьте гипотенузу как c, а более короткие стороны — как a и b. Неважно, какой катет вы обозначите буквой a, а какой — буквой b, так как это не повлияет на конечный результат.
4
Подставьте в формулу значения известных сторон. Помните, что a² + b² = c². Вместо букв подставьте числа, данные в условии задачи.
- Предположим, в условии дано, что a = 3 и b = 4, тогда получаем: 3² + 4² = c².
- Если катет a = 6 и гипотенуза c = 10, тогда можно записать: 6² + b² = 10².
5
Решите полученное уравнение, чтобы найти неизвестную сторону. Для этого сначала возведите в квадрат известные длины сторон (просто умножьте данное число само на себя, например 3² = 3 * 3 = 9). Если вы ищете гипотенузу, сложите квадраты двух сторон и из полученной суммы извлеките квадратный корень. Если необходимо найти катет, вычтите квадрат известного катета из квадрата гипотенузы и из полученного числа извлеките квадратный корень.
- В первом примере складываем квадраты сторон 3² + 4² = c² и получаем 25= c². После этого извлекаем квадратный корень из 25 и находим c = 5.
- Во втором примере складываем квадраты сторон 6² + b² = 10² и получаем 36 + b² = 100. Переносим 36 в правую сторону уравнения: b² = 64. Извлекаем квадратный корень из 64 и находим b = 8.
6
Сложите длины трех сторон, чтобы найти периметр. Как мы помним, периметр вычисляется по формуле: P = a + b + c. После того как мы нашли длины сторон a, b и c, необходимо сложить их, чтобы определить периметр.
- В первом примере: P = 3 + 4 + 5 = 12.
- Во втором примере: P = 6 + 8 + 10 = 24.
Реклама

1

Выучите теорему косинусов. Эта теорема позволяет вычислить неизвестную сторону треугольника, если даны длины двух других сторон и величина угла между ними. Теорема косинусов очень полезна, она справедлива для всех треугольников. Эта теорема гласит, что для любого треугольника со сторонами a, b и c и противолежащими им углами A, B и C справедлива следующая формула: c² = a² + b² – 2ab cos(C).^[3]^[4]
2
Дайте обозначения сторонам и углам треугольника. Обозначьте первую известную сторону как a, а противоположный ей угол — как A. Вторую известную сторону и противолежащий ей угол обозначьте соответственно b и B. Известный угол между этими сторонами обозначьте как C, а противолежащую ему сторону, длину которой необходимо найти, — как c.
- Предположим, дан треугольник со сторонами 10 и 12 и углом между ними 97°. В этом случае имеем: a = 10, b = 12, C = 97°.
3
Подставьте известные значения в формулу и найдите неизвестную сторону с. Сначала возведите в квадрат длины известных сторон и сложите полученные значения. Затем найдите косинус угла С с помощью обычного или онлайн-калькулятора.^[5] Умножьте cos(C) на 2ab и вычтите полученное число из суммы a² + b². В результате вы получите c². Извлеките квадратный корень, чтобы найти длину неизвестной стороны c. В нашем примере имеем:
- c² = 10² + 12² – 2 × 10 × 12 × cos(97°).
- c² = 100 + 144 – (240 × -0,12187) (мы округлили значение косинуса до 5 знаков после запятой).
- c² = 244 – (-29,25).
- c² = 244 + 29,25 (два минуса дают плюс!).
- c² = 273,25.
- c = 16,53.
4
Используйте вычисленную длину стороны c, чтобы найти периметр треугольника. Напомним, что периметр вычисляется по формуле: P = a + b + c, то есть следует прибавить к известным величинам сторон a и b найденную длину стороны c.
- В нашем примере получаем: 10 + 12 + 16,53 = 38,53. Итак, периметр треугольника равен 38,53!
Реклама

Об этой статье

Эту страницу просматривали 270 082 раза.

Была ли эта статья полезной?

Источник

Как найти периметр треугольника

Содержание:

Периметр треугольника
Способы нахождения
- По трем сторонам
- По площади и радиусу вписанной окружности
- По двум сторонам и углу между ними
- По боковой стороне и высоте (для равнобедренного)
- По двум катетам (для прямоугольного)
Примеры решения задач
- Задача №1
- Задача №2
- Задача №3
- Задача №4
- Задача №5

Треугольник

Учимся находить периметр треугольника разными способами, а также тренируем полученные знания на примерах задач.

Периметр треугольника

Определение

Периметр треугольника — это сумма длин всех его сторон.

Определение

Треугольник — это геометрическая фигура, которая состоит из трех точек (вершин), не лежащих на одной прямой. Эти точки попарно соединены тремя отрезками, которые называются сторонами (ребрами) многоугольника.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Рассмотрим несколько способов нахождения периметра рассматриваемой фигуры. Каждая из предложенных формул опирается на те величины, которые нам уже известны.

Способы нахождения

По трем сторонам

Источник: cdn.lifehacker.ru

Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:

(P = a+b+c)

где a, b и с — это стороны треугольника.

В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:

(P=a+2b) или (P=a+2c )

где a — основание фигуры, а b и с — равные ребра.

Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:

(P=3a)

где a — это любая сторона фигуры.

По площади и радиусу вписанной окружности

Источник: cdn.lifehacker.ru

Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:

(P=frac{2S}r)

где S — площадь фигуры, r — радиус вписанной в нее окружности.

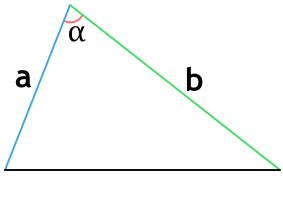
По двум сторонам и углу между ними

Источник: cdn.lifehacker.ru

Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.

Теорема косинусов выглядит так:

(a^2=b^2+c^2-2bctimescosalpha)

где α — известный угол.

Тогда формула для расчета периметра всей фигуры в этом случае:

(P=sqrt{b^2+c^2-2bctimescosalpha}+b+c)

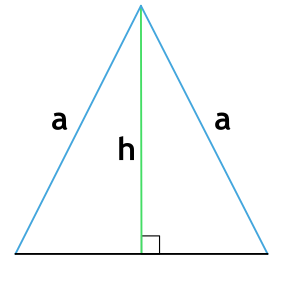
По боковой стороне и высоте (для равнобедренного)

Источник: cdn.lifehacker.ru

Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.

Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:

(d^2=a^2-h^2)

(d=sqrt{a^2-h^2})

где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.

Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.

(P=2sqrt{a^2-h^2}+2a)

По двум катетам (для прямоугольного)

Источник: cdn.lifehacker.ru

Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).

(c^2=a^2+b^2)

(c=sqrt{a^2+b^2})

где a и b — катеты треугольника.

Подставляем значение c в формулу для нахождения периметра и получаем:

(P=sqrt{a^2+b^2}+a+b)

Примеры решения задач

Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.

Задача №1

Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.

Решение:

Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.

Ответ: 16 см.

Задача №2

Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.

Решение:

Для данного случая подходит формула P=a+2b, подствляем значения: (P=6+4times2 = 14) см.

Ответ: 14 см.

Задача №3

Нам известно, что площадь треугольника — 24 см², а радиус вписанной в него окружности — 8 см. Найти P.

Решение:

В данном случае рассчитывать P будем следующим образом: (P=frac{2S}r). С уже известными нам величинами получаем: (P=frac{2times24}8 = 6) см.

Ответ: 6 см.

Задача №4

Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.

Решение:

Мы знаем, что в этом случае P вычисляется, как (P=2sqrt{a^2-h^2}+2a). С имеющимися значениями получается: (P=2sqrt{4^2-2^2}+2times2 = 4sqrt3+4) см.

Ответ: P=4sqrt3+4 см.

Задача №5

Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.

Решение:

В формулу (P=sqrt{a^2+b^2}+a+b) подставляем известные значения: (P=sqrt{5^2+7^2}+5+7 = sqrt{74}+12) см.

Ответ: (P=sqrt{74}+12) см.

Насколько полезной была для вас статья?

Рейтинг: 4.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

{P=a+b+c}

Чтобы найти периметр треугольника необходимо сложить длины трех его сторон. Однако, существует множество других формул, которые позволяют рассчитать периметр треугольника. На странице мы собрали самые известные формулы для расчета периметра треугольника, а также удобный калькулятор.

Содержание:

калькулятор периметра треугольника
формула периметра треугольника через стороны
формула периметра треугольника по средним линиям
формула периметра треугольника по двум сторонам и углу между ними
формула периметра прямоугольного треугольника по катету и гипотенузе
формула периметра прямоугольного треугольника по катетам
формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу
формула периметра прямоугольного треугольника по катету и прилежащему углу
формула периметра прямоугольного треугольника по катету и противолежащему углу
формула периметра равнобедренного треугольника по боковой стороне и высоте
формула периметра равнобедренного треугольника по основанию и высоте
формула периметра равнобедренного треугольника по боковой стороне и основанию
формула периметра равностороннего треугольника по высоте
формула периметра равностороннего треугольника через площадь вписанной окружности
примеры задач

Треугольник — геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки.

Формула периметра треугольника через стороны

{P = a+b+c}

a, b и c — стороны треугольника

Формула периметра треугольника по средним линиям

Средняя линия треугольника — отрезок, который соединяет середины двух сторон.

{P=2a+2b+2c}

a, b и c — средние линии треугольника

Формула периметра треугольника по двум сторонам и углу между ними

{P=a+b+sqrt{a^2+b^2-2ab cdot cos(alpha)}}

a и b — стороны треугольника

α — угол между сторонами a и b

Формула периметра прямоугольного треугольника по катету и гипотенузе

Прямоугольный треугольник — это треугольник, в котором один угол прямой (90 градусов).

{P = a+c+sqrt{c^2-a^2}}

a — катет прямоугольного треугольника

c — гипотенуза прямоугольного треугольника

Формула периметра прямоугольного треугольника по катетам

{P = a+b+sqrt{a^2+b^2}}

a и b — катеты прямоугольного треугольника

Формула периметра прямоугольного треугольника по гипотенузе и прилежащему углу

{P=csin(alpha)+ccos(alpha)+c}

c — гипотенуза прямоугольного треугольника

α — прилежащий к гипотенузе угол

Формула периметра прямоугольного треугольника по катету и прилежащему углу

{P=a \tg(alpha)+a+dfrac{a}{cos(alpha)}}

a — катет прямоугольного треугольника

α — прилежащий к катеру угол

Формула периметра прямоугольного треугольника по катету и противолежащему углу

{P=a+dfrac{a}{\tg(alpha)}+dfrac{a}{sin(alpha)}}

a — катет прямоугольного треугольника

α — противолежащий к катеру угол

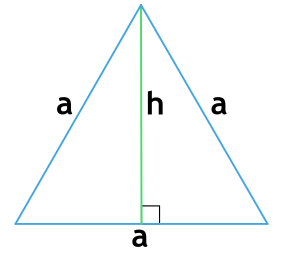
Формула периметра равнобедренного треугольника по боковой стороне и высоте

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.

{P = 2a+2sqrt{a^2-h^2}}

a — боковая сторона равнобедренного треугольника

h — высота равнобедренного треугольника

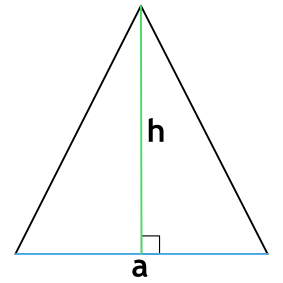
Формула периметра равнобедренного треугольника по основанию и высоте

{P = a+2sqrt{Big( Big(dfrac{a}{2} Big)^2+h^2 Big)}}

a — основание равнобедренного треугольника

h — высота равнобедренного треугольника

Формула периметра равнобедренного треугольника по боковой стороне и основанию

{P=2b+a}

a — основание равнобедренного треугольника

b — боковая сторона равнобедренного треугольника

Формула периметра равностороннего треугольника по высоте

Равносторонний треугольник —треугольник, у которого все стороны равны.

{P=2sqrt{3}h}

h — высота равностороннего треугольника

Формула периметра равностороннего треугольника через площадь вписанной окружности

{P = 6sqrt{dfrac{3S}{pi}}}

S — площадь вписанной в равносторонний треугольник окружности

Примеры задач на нахождение периметра треугольника

Задача 1

Найдите периметр треугольника, если его средние линии равны 6см 9см и 10см.

Решение

Для решения задачи применим формулу №2. Подставим в нее длины средних линий и произведем вычисления.

P = 2a+2b+2c = 2 cdot 6 + 2 cdot 9 + 2 cdot 10 = 12 + 18 + 20 = 50 : см

Ответ: 50 см

Ответ проверим с помощью калькулятора .

Задача 2

Найдите периметр треугольника со сторонами 14см, 17см и 17см.

Решение

А для этой задачи подойдет первая формула.

P = a+b+c = 14 + 17 + 17 = 48 : см

Если обратить внимание на то, что у треугольника в условии две стороны имеют одинаковую длину, то можно понять, что данный треугольник равнобедренный. И тогда задачу можно решить используя формулу для равнобедренного треугольника.

P=2b+a = 2 cdot 17 + 14 = 34 + 14 = 48 : см

Ответ: 48 см

Проверим ответ по первой и второй формуле.

Задача 3

Найдите периметр прямоугольного треугольника, если его катеты равны 12см и 16см.

Решение

Воспользуемся подходящей формулой.

P = a+b+sqrt{a^2+b^2} = 12+16+sqrt{12^2+16^2} = 28+sqrt{144+256} = 28+sqrt{400} = 28+20 = 48 : см

Ответ: 48 см

Полученный результат удобно проверить с помощью калькулятора .

Задача 4

Найдите периметр равнобедренного треугольника основание которого равно 13см а боковая сторона 8см.

Решение

Для равнобедренного треугольника, у которого известно основание и боковая сторона нам подходит эта формула.

P=2b+a = 2 cdot 8 + 13 = 16 + 13 = 29 : см

Ответ: 29 см

Проверка .

Задача 5

Найдите периметр равностороннего треугольника, если его высота равна 9см.

Решение

Для равностороннего треугольника с известной высотой мы применим эту формулу.

P = 2sqrt{3}h = 2sqrt{3} cdot 9 = 18sqrt{3} : см approx 31.17691 : см

Ответ: 18sqrt{3} : см approx 31.17691 : см

Проверить ответ поможет калькулятор .

Источник

Основные определения

Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.

Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.

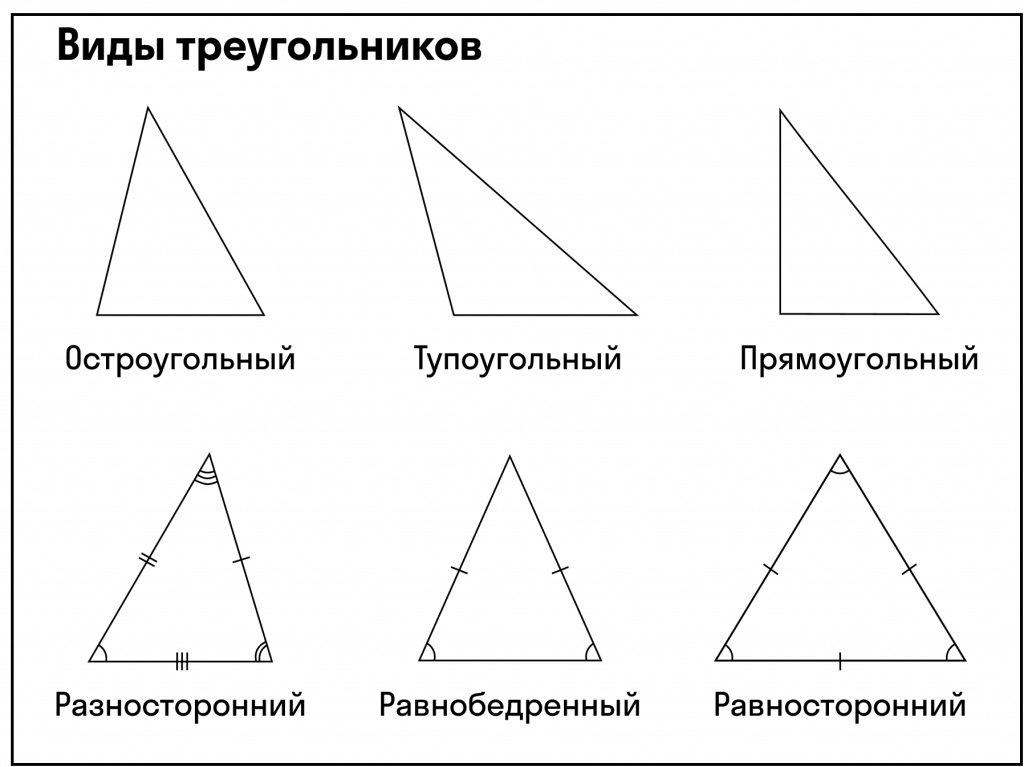
Понятия

Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).

Вершины треугольника – это точки, где соединяются 2 стороны фигуры.

Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.

Р/с треугольник – это треугольник, у которого все стороны равны между собой.

Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.

Прямоугольный треугольник — это треугольник, у у которого один угол равен 90^о. Самая длинная сторона называется гипотенузой, а две другие катетами.

Формула нахождения периметра

Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.

Задача 1

Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.

Решение: [P=13+15+12=40] см.

Ответ: 40 см.

Периметр разностороннего треугольника

В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2

Задача 2

Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.

Решение:

P = 30 + 25 + 15 = 70 дм

70 : 10 = 7 м

Ответ: 7 м.

Периметр равнобедренного треугольника

Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.

Задачи 3 — 4

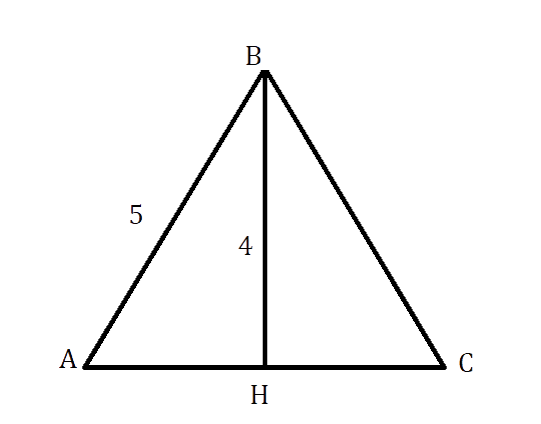
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.

Решение:

Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.

В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см

АН = НС = √9 = 3 см

АС = АН + НС = 3 + 3 = 6 см

Р = 6 + 2*5 = 16 см

Ответ: 16 см.

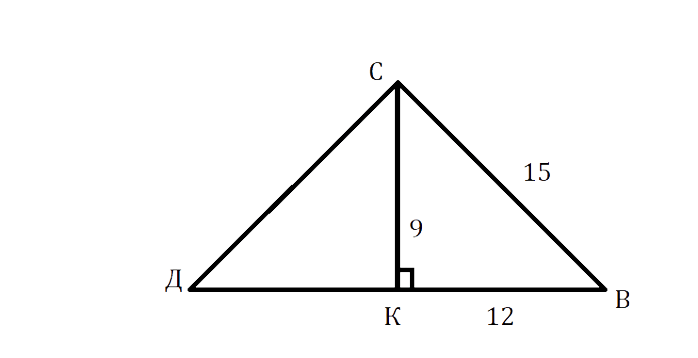
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.

Решение:

В ΔСКД по теореме Пифагора:

[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см

ДК = √144 = 12 см.

Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.

Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.

Ответ: 54 см.

Нет времени решать самому?

Наши эксперты помогут!

Периметр равностороннего треугольника

А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.

Задачи 5 — 6

Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.

Решение:

Р = 3а = 3 * 13 = 39

Ответ: 39.

В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.

Решение:

Р = 3АВ = 15 * 3 = 45 см.

Ответ: 45 см.

Периметр прямоугольного треугольника

Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.

Задачи 7 — 8

Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.

Решение:

По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]

с = √100 = 10

Р = а + в + с = 6 + 8 + 10 = 24

Ответ: 24.

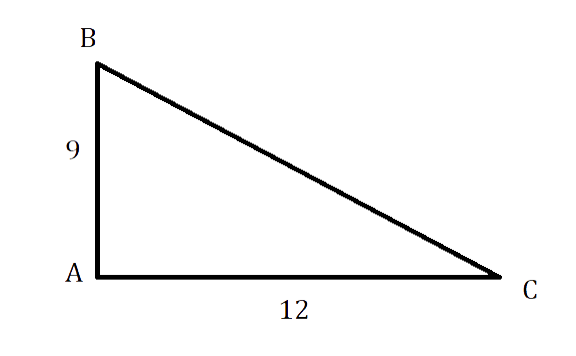
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.

Решение

По теореме Пифагора в ΔАВС:

[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]

СВ = √225 = 15 см

S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см

P = 15 + 9 + 12 = 36 см

Ответ: 36 см; 54 см.

Источник