Как найти периметр треугольника по координатам векторов

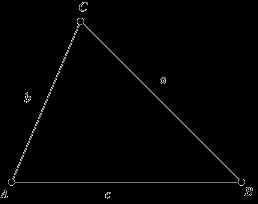
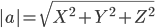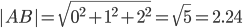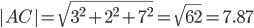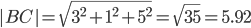Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам: Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 4 года назад  Периметр по координатам Периметр фигуры — это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2): Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой: Нужно взять лист бумаги в клетку (или даже миллиметровую бумагу) и начертить систему координат. Отмечаем на ней все точки и соединяем их линиями. Затем с помощью линейки измеряем длину каждой линии и складываем все значения. Sadne­ss [5.6K] 4 года назад  Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так: l=sqrt((x2 — x1)^2 + (y2 — y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере: Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((12 — 1)^2 + ((-5) — 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((-2 — 12)^2 + (1 — -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 — (-2))^2 + (8 — 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты. Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым — просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула: , где х1 и х2 — координаты концов отрезка по оси х, а y1 и y2 — координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины. Hamst­er133­7 [28.6K] 2 года назад  Периметр геометрических фигур по координатам вершин можно найти при помощи формулы Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр. Алиса в Стран­е [364K] 3 года назад  Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр — сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула: где точка А имеет координаты (x1; y1), а точка В — координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС. габба­с [215K] 4 года назад  Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 — x1^2) + (y2^2 — y1^2), х1 и у1 координаты начала, х2,у2 — координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюми­нка [59.9K] 3 года назад  Во-первых, вспомним, что такое периметр — это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb — xa)2 + (yb — ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2): Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить — получить. Бекки Шарп [71.2K] 3 года назад  Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле: У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле. Складываем полученные результаты и получаем периметр. Барха­тные лапки [382K] 3 года назад  Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр. Знаете ответ?

Как найти периметр треугольника, заданного координатами своих вершин

Периметр — это длина линии, ограничивающей занимаемую плоской геометрической фигурой площадь. Для треугольника, как и всех других многоугольников, это ломаная линия, составленная из его всех его сторон. Поэтому задача вычисления периметра треугольника, заданного координатами его вершин, сводится к вычислению длины каждой из сторон с последующим суммированием полученных величин.

Инструкция

Чтобы вычислить длину стороны, рассмотрите вспомогательный треугольник, составленный из самой стороны и двух ее проекций на оси абсцисс и ординат. В этой фигуре две проекции будут образовывать прямой угол — это вытекает из определения прямоугольных координат. Это означает, что они будут катетами в прямоугольном треугольнике, где гипотенузой будет сама сторона. Ее длину можно вычислить по теореме Пифагора, надо лишь найти длины проекций (катетов). Каждая из проекций представляет собой отрезок, начальная точка которого определена меньшей координатой, конечная — большей, а их разница и будет длиной проекции.

Рассчитайте длину каждой стороны. Если обозначить координаты точек, определяющих треугольник, как A(X₁,Y₁), B(X₂,Y₂) и C(X₃,Y₃), то для стороны АВ проекции на оси абсцисс и ординат будут иметь длины X₂-X₁ и Y₂-Y₁, а длина самой стороны в соответствии с теоремой Пифагора будет равна АВ = √((X₂-X₁)² + (Y₂-Y₁)²). Длины двух других сторон, рассчитанные через их проекции на оси координат, можно записать так: ВС = √(( X₃-X₂)² + (Y₃-Y₂)²), СА = √((X₃-X₁)² + (Y₃-Y₁)²).

При использовании трехмерной системы координат в подкоренное выражение, полученное на предыдущем шаге, добавьте еще одно слагаемое, которое должно выражать квадрат длины проекции стороны на ось аппликат. В этом случае координаты точек можно записать так: A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃). А формулы расчета длин сторон примут такой вид: АВ = √((X₂-X₁)² + (Y₂-Y₁)² + (Z₂- Z₁)²), ВС = √(( X₃-X₂)² + (Y₃-Y₂)² + (Z₃-Z₂)²) и СА = √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).

Рассчитайте периметр (Р) треугольника, сложив полученные на предыдущих шагах длины сторон. Для плоской Декартовой системы координат формула в общем виде должна выглядеть так: Р = АВ + ВС + СА = √((X₂-X₁)² + (Y₂-Y₁)²) + √(( X₃-X₂)² + (Y₃-Y₂)²) + √((X₃-X₁)² + (Y₃-Y₁)²). Для трехмерных координат эта же формула должна иметь такой вид: Р = √((X₂-X₁)² + (Y₂-Y₁)² + (Z₂- Z₁)²) + √(( X₃-X₂)² + (Y₃-Y₂)² + (Z₃-Z₂)²) + √((X₃-X₁)² + (Y₃-Y₁)² + (Z₃-Z₁)²).

Источники:

• площадь треугольника заданного координатами вершин

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Находим периметр треугольника различными способами

Периметр любого треугольника – это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех сторон этого многоугольника.

Вычисление по данным значениям длины сторон

Когда известны их значения, то сделать это несложно. Обозначив эти параметры буквами m, n, k, а периметр буквой P, получим формулу для вычисления: P = m+n+k. Задание: Известно, что треугольник имеет стороны длиной 13,5 дециметров, 12,1 дециметров и 4,2 дециметра. Узнать периметр. Решаем: Если стороны данного многоугольника — a = 13,5 дм, b = 12,1 дм, c = 4,2 дм, то P = 29,8 дм. Ответ: P = 29,8 дм.

Периметр треугольника, который имеет две равные стороны

Такой треугольник называется равнобедренным. Если эти равные стороны имеют длину a сантиметров, а третья сторона – b сантиметров, то периметр легко узнать: P =b+2a. Задание: треугольник имеет две стороны по 10 дециметров, основание 12 дециметров. Найти P. Решение: Пусть боковая сторона a = c = 10 дм, основание b = 12 дм. Сумма сторон P = 10 дм + 12 дм + 10 дм = 32 дм. Ответ: P = 32 дециметра.

Периметр равностороннего треугольника

Если все три стороны треугольника имеют равное количество единиц измерения, он называется равносторонним. Еще одно название – правильный. Периметр правильного треугольника находят при помощи формулы: P = a+a+a = 3·a. Задача: Имеем равносторонний треугольный земельный участок. Одна сторона равна 6 метрам. Найти длину забора, которым можно обнести этот участок. Решение: Если сторона этого многоугольника a= 6м, то длина забора P = 3·6 = 18 (м). Ответ: P = 18 м.

Треугольник, у которого есть угол 90°

Его называют прямоугольным. Наличие прямого угла дает возможность находить неизвестные стороны, пользуясь определением тригонометрических функций и теоремой Пифагора. Самая длинная сторона называется гипотенуза и обозначается c. Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c 2 = a 2 + b 2 . Катеты a = √ (c 2 – b 2 ) и b = √ (c 2 – а 2 ). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,3 2 + 6,2 2 ) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,3 2 + 6,2 2 ) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых. Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c 2 – b 2 ) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов – 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (12 2 – 8 2 ) = 20 + √80 = 20 + 8,9 = 28,9 (км). Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А – 29 градусов. Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых. Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол – 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см. Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого – на синус и для второго – на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см). Значит периметр этого многоугольника равен P = 9,1 + 7 + 5,8 = 21,9 (см). Или P = 9,1·(1 + 0,77 + 0,64) = 21,9 (см). Ответ: P = 21,9 сантиметров.

Произвольный треугольник, одна из сторон которого неизвестна

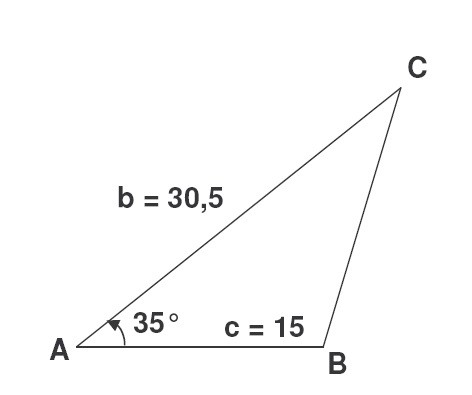
Если мы имеем значения двух сторон a и c, и угла между этими сторонами γ, третью находим теоремой косинусов: b 2 = с 2 + a 2 – 2 ас cos β, где β – угол, лежащий между сторонами а и с. Затем находим периметр. Задание: Δ АВС имеет отрезок АВ длиной 15 дм, отрезок АС, длина которго 30,5 дм. Значение угла между этими сторонами 35 градусов. Вычислить сумму сторон Δ АВС. Решение: Теоремой косинусов вычислим длину третей стороны. BC 2 = 30,5 2 + 15 2 — 2·30,5·15·0,82 = 930,25 + 225 – 750,3 = 404,95. BC = 20,1 см. P = 30,5 + 15 + 20,1 = 65,6 (дм).Имеем: P = 65,6 дм.

Сумма сторон произвольного треугольника, у которого длины двух сторон неизвестны

Когда знаем длину только одного отрезка и значение двух углов, можно узнать длину двух неизвестных сторон, пользуясь теоремой синусов: «в треугольнике стороны всегда пропорциональны значениям синусов противоположных углов». Откуда b = (a* sin β)/ sin a. Аналогично c = (a sin γ): sin a. Периметр в таком случае будет P = а + (а sin β)/ sin a + (a sin γ)/ sin a. Задание: Имеем Δ ABC. В нем длина стороны BC 8,5 мм, значение угла C – 47°, а угла B – 35 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим длины сторон BC = a = 8,5 мм, AC = b, AB = c, ∟ A = α= 47°, ∟B = β = 35°, ∟ C = γ = 180° – (47° + 35°) = 180° – 82° = 98°. Из соотношений, полученных из теоремы синусов, находим катеты AC = b = (8,5·0,57): 0,73= 6,7 (мм), AB = c = (7 · 0,99): 0,73 = 9,5 (мм). Отсюда сумма сторон этого многоугольника равна P = 8,5 мм + 5,5 мм + 9,5 мм = 23,5 мм. Ответ: P = 23,5 мм. В случае, когда есть только длина одного отрезка и значения двух прилежащих углов, сначала вычисляем угол, противоположный известной стороне. Все углы этой фигуры в сумме имеют 180 градусов. Поэтому ∟A = 180° — (∟B + ∟C). Дальше находим неизвестные отрезки, используя теорему синусов. Задание: Имеем Δ ABC. Он имеет отрезок BC, равный 10 см. Значение угла B равно 48 градусов, угол C равен 56 градусов. Найти сумму сторон Δ ABC. Решение: Сначала найдем значение угла A, противолежащего стороне BC. ∟A = 180° – (48° + 56°) = 76°. Теперь с теоремой синусов вычислим длину стороны AC = 10·0,74: 0,97 = 7,6 (см). AB = BC* sin C/ sin A = 8,6. Периметр треугольника Р = 10 + 8,6 + 7,6 = 26,2 (см). Результат: P = 26,2 см.

Вычисление периметра треугольника с использованием радиуса окружности, вписанной в него

Иногда из условия задачи не известна ни одна сторона. Зато есть значение площади треугольника и радиуса окружности, вписанной в него. Эти величины связаны: S = r p. Зная значение площади треугольника, радиуса r, можем найти полупериметр p. Находим p = S: r. Задача: Участок имеет площадь 24 м 2 , радиус r равен 3 м. Найти количество деревьев, которое нужно высадить равномерно по линии, ограждающей этот участок, если между двумя соседними должно быть расстояние 2 метра. Решение: Сумму сторон данной фигуры находим так: P = 2 · 24: 3 = 16 (м). Затем делим на два. 16:2= 8. Итого: 8 деревьев.

Сумма сторон треугольника в декартовых координатах

Вершины Δ АВС имеют координаты: A (x₁; y₁), B (x₂; y₂), C(x₃ ; y₃). Найдем квадраты каждой из сторон AB 2 = (x₁ — x₂) 2 + (y₁ — y₂) 2 ; ВС 2 = (x₂ — x₃) 2 + (y₂ — y₃) 2 ; АС 2 = (x₁ — x₃) 2 + (y₁ — y₃) 2 . Чтобы найти периметр, достаточно сложить все отрезки. Задание: Координаты вершин Δ ABC: B (3; 0), A (1; -3), C (2; 5). Найти сумму сторон этой фигуры. Решение: поставив значения соответствующих координат в формулу периметра, получим P = √(4 + 9) + √(1 + 25) + √(1 + 64) = √13 + √26 + √65 = 3,6 + 5,1 + 8,0 = 16,6. Имеем: P = 16,6. Если фигура находится не на плоскости, а в пространстве, то каждая из вершин имеет три координаты. Поэтому формула суммы сторон будет иметь еще одно слагаемое.

Векторный метод

Если фигура задана координатами вершин, периметр можно вычислить, используя векторный метод. Вектор – отрезок, имеющий направление. Его модуль (длина) обозначается символом ǀᾱǀ. Расстояние между точками – это и есть длина соответствующего вектора, или модуль вектора. Рассмотрим треугольник, лежащий на плоскости. Если вершины имеют координаты А (х₁; у₁), М(х₂; у₂), Т (х₃; у₃), то длину каждой из сторон находим по формулам: ǀАМǀ = √ ((х₁ – х₂) 2 + (у₁ – у₂) 2 ), ǀМТǀ = √ ((х₂ – х₃) 2 + (у₂ – у₃) 2 ), ǀАТǀ = √ ((х₁ – х₃) 2 + (у₁ – у₃) 2 ). Периметр треугольника получим, сложив длины векторов. Аналогично находят сумму сторон треугольника в пространстве.

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Как найти периметр треугольника

Решение.
1) Координаты векторов
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i; Z = z_j — z_i
здесь X,Y,Z координаты вектора; x_i, y_i, z_i — координаты точки А_i; x_j, y_j, z_j — координаты точки А_j;
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁; Z = z₂ — z₁
X = 2-2; Y = 0-1; Z = 5-3
AB(0;-1;2)
AC(3;-2;7)
BC(3;-1;5)

2) Модули векторов
Длина вектора a(X;Y;Z) выражается через его координаты формулой:




т.е. периметр равен Р = 2.236 + 7.874 + 5.916 =16.026.

ПОМОГИТЕ МНЕ ПОЖАЛУЙСТА. По координатам вершин треугольника ABC найти: периметр треугольника; уравнения сторон AB и BC; уравнение высоты AD; угол ABC; площадь треугольника. Сделать чертеж.
А(3; 3); В(–3; –3); С(3; 5).

Даны координаты вершин треугольника ABC: А(3; 3); В(–3; –3); С(3; 5).

1) Периметр треугольника.

Расчет длин сторон

АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √72 = 6√2 ≈ 8,48528.

BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √100 = 10.

AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √4 = 2.

Периметр равен 12 + 6√2 ≈ 20,48528.

2) Уравнения сторон AB и BC.

х — у = 0 общее уравнение,

у = х уравнение с угловым коэффициентом (к = 1).

Хс-Хв Ус-Ув 6 8, сократить на 2:

у = (4/3)х + 1.

3) Уравнение высоты AD.

к(АД) = -1/к(ВС) = -1/(4/3) = -3/4.

у = (-3/4)х + в. Подставим точку А(3; 3): 3 = (-3/4)*3 + в, в = 3 + (9/4) = 21/4.

Уравнение АД: (-3/4)х + (21/4).

cos В= АВ²+ВС²-АС² = 0,98995.

B = 0,141897 радиан,

B = 8,130102 градусов.

5) Площадь S треугольника ABC равна:

Площадь можно найти по формуле Герона: S = √(p(p-a)(p-b)(p-c)).

Полупериметр p = 10,24264. S = 6.

6) Сделать чертеж — построить точки А, В и С по координатам и соединить отрезками.

Периметр многоугольника по его координатам

В данной статье мы окажем помощь в расчете периметра многоугольника, заданного координатами его вершин. Несмотря на то, что сам принцип расчета прост, при большом количестве вершин, Вам придется делать несколько раз одни и те же вычисления, то есть выполнять рутинную операцию. А я страсть как не люблю рутину и Вам ей заниматься не советую.

Формула которая используется проста:

Если извеcтны две точки с координатами (x1,y1) и (x2,y2) то расстояние между ними

эту формулу необходиом применить к каждой паре координат соседних вершин многоугольника. И как только мы закончим обход и просуммировав все длины мы получим наш периметр.

Теперь что касается ввода данных. В предыдущем материале Площадь многоугольника по координатам онлайн ввод координат осуществляется через двоеточие и пробел, что не совсем удобно.

В этой статье, для упрощения и для обощения ( на комплексное представление) коодинаты будут задаватся в виде комплексных чисел.

Для тех кто с комплексными числами никогда не сталкивался, хочу успокоить — ничего страшного.

И если Вы координату раньше представляли как (x,y), то в комплексном представлении эта же координата видится уже как x+iy

Для ввода это немного проще, так как в дальнейшем при написании статьи про линейные преобразования фигуры на плоскости, это форма ввода нам пригодится, да и понимать ту статью Вам будет уже намного проще.

Теперь немного примеров:

Определим периметр многоугольника заданного координатами А (0; 0); В (8; 2); С (–2; 6).

Так как три вершины то это треугольник.

Введем данные в поле ввода( разделяя каждую координату вершины пробелом) в таком формате 0+0i 8+2i -2+6i

Обзор основных сведений и формул для векторов в координатах

В координатной плоскости любой вектор  однозначно разлагается по векторам  и  

Числа  определяются единственным образом и называются координатами вектора  в данной системе координат (рис. 1).

Рис. 1. Координаты вектора

Если есть точка , то вектор с началом в начале координат, который называется радиус-вектором точки , имеет те же самые координаты: .

Основываясь на этом, мы рассмотрели 3 стандартные задачи:

Определение координат середины отрезка по координатам концов отрезка и  

Рис. 2. Иллюстрация к задаче

Определение длины вектора  с координатами .

 

Определение длины отрезка  по координатам концов  и .

Теперь применим эти сведения для решения задач.

Решение задач с использованием метода координат

Задача 1.

Рис. 3. Иллюстрация к задаче

Дан треугольник с вершинами . Найти медиану .     

Дано:

           ;

           

           

Найти: .

Решение:

Найдем координаты точки  как середины отрезка ВС:

Найдем длину отрезка :

.

Ответ: .

Задача 2.

Вершина  параллелограмма  лежит на положительной полуоси , вершина  имеет координаты ; . Найти координаты точки  сторону  диагональ .

Решение:

Построим данный параллелограмм в прямоугольной системе координат (рис. 4).

Рис. 4. Иллюстрация к задаче

Так как , то координаты точки  . Пусть координаты точки .

Так как  параллелограмм, то ;

Координаты равны, следовательно,

Итак, ;

 так как вектор  имеет те же координаты, что и точка .

 так как координаты вектора  совпадают с координатами точки

Ответ: ;

Задача 3.

Найти периметр треугольника, если известны координаты его вершин (рис. 5).

Рис. 5. Иллюстрация к задаче

Дано: 

            

            ;

 .

Найти: периметр .

Решение:

Воспользуемся формулой вычисления расстояния между точками.

Найдем длину :

Найдем длину :

Найдем длину :

Найдем периметр:

Ответ:

Заключение

Мы сделали обзор сведений о координатах, о простейших задачах и применили эти сведения для решения конкретных геометрических задач.

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. E-science.ru (Источник).
2. E-science.ru (Источник).
3. Mathematics.ru (Источник).

Домашнее задание

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010., №№ 943, 945, 947.