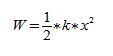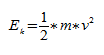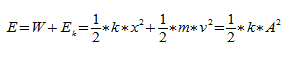Формула периода колебаний пружинного маятника в физике
Формула периода колебаний пружинного маятника
Определение
Период — это минимальное время, за которое совершается одно полное колебательное движение.
Обозначают период буквой $T$.
[T=frac{Delta t}{N}left(1right),]
где $Delta t$ — время колебаний; $N$ — число полных колебаний.
Уравнение колебаний пружинного маятника
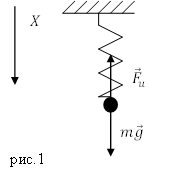
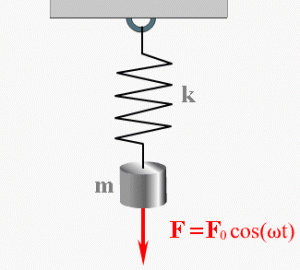
Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.
Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:
[mg=kb left(2right).]
Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
[F_u=-kleft(x+bright)left(3right).]
Ускорение груза запишем, помня, что движение происходит по оси X, как:
[a=frac{d^2x}{dt^2}=ddot{x }left(4right).]
Второй закон Ньютона для груза принимает вид:
[mddot{x}=-kleft(x+bright)+mg left(5right).]
Учтем равенство (2), формулу (5) преобразуем к виду:
[mddot{x}=-kx-kb+mg=-kx-mg+mg=-kx left(6right).]
Если ввести обозначение: ${omega }^2_0=frac{k}{m}$, то уравнение колебаний запишем как:
[ddot{x}+{omega }^2_0x=0left(7right),]
где ${omega }^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(8right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.
Формулы периода колебаний пружинного маятника
Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний.
Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(9right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(10right).]
Выше мы получали для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(11right).]
Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Примеры задач на период колебаний
Пример 1
Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?
Решение. Так как период — это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:
[T=frac{Delta t}{N}left(1.1right).]
Вычислим период:
[T=frac{10}{50}=0,2 left(сright).]
Частота — величина обратная периоду, следовательно:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту колебаний:
[nu =frac{1}{0,2}=5 left(Гцright).]
Ответ. $1) T=0,2$ с; 2) 5Гц
Пример 2
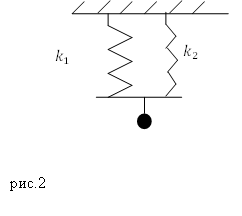
Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?
Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:
[T=2pi sqrt{frac{M}{k}} left(2.1right).]
При параллельном соединении пружин результирующая жесткость системы находится как:
[k=k_1{+k}_2left(2.2right).]
Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{M}{k_1{+k}_2}}.]
Ответ. $T=2pi sqrt{frac{M}{k_1{+k}_2}}$
Читать дальше: формула плеча силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.
Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.
В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.
Что такое пружинный маятник
Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.
Приняты следующие обозначения:
-
m — масса тела;
-
k — коэффициент жесткости пружины.
Общий вид маятника:
Особенностями пружинных маятников являются:
-
Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;
-
У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;
-
Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;
-
Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;
-
От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.
Виды пружинных маятников
Существует два типа данной системы:
-
Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.
-
Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.
Сила упругости в пружинном маятнике
До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.
Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.
Расчёт силы упругости может быть проведен таким образом:
Fупр = — k*x
где k — коэффициент жесткости пружины (Нм),
x – смещение (м).
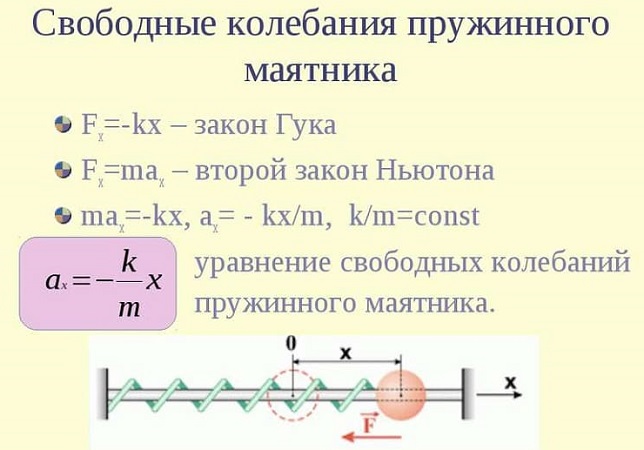
Уравнения колебаний пружинного маятника
Свободные колебания пружинного маятника описываются с помощью гармонического закона.
Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:
F(t) = ma(t) = — mw2x(t),
где w — радиальная частота гармонического колебания.
Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:
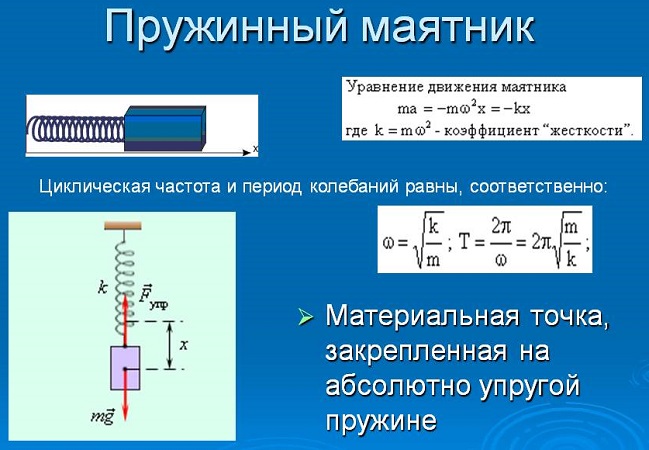
Период и частота свободных колебаний пружинного маятника
При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.
Изменение циклической частоты покажет формула, приведенная на рисунке:
Факторы, от которых зависит частота:
-
Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.
-
Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.
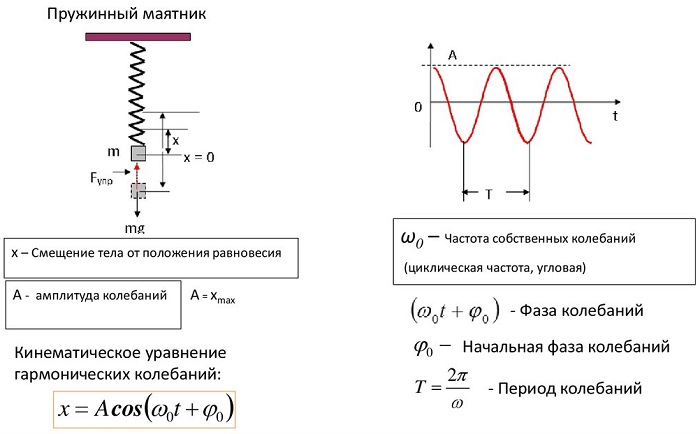
Амплитуда и начальная фаза пружинного маятника
Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.
В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).
Энергия пружинного маятника
При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.
Потенциальная энергия:
Кинетическая энергия:
Полная энергия:
Расчет имеет особенности. При его проведении нужно учитывать несколько условий:
-
Колебания проходят в двух плоскостях: вертикальной и горизонтальной.
-
В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.
-
Влияние силы трения при расчете не учитывают.
Дифференциальное уравнение гармонических колебаний пружинного маятника
Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.
Механическая колебательная система, состоящая из пружины с коэффициентом упругости (жёсткостью) (k), один конец которой жёстко закреплён, а на втором находится груз массы (m), называется пружинным маятником.
Рис. (1). Колебания пружинного маятника
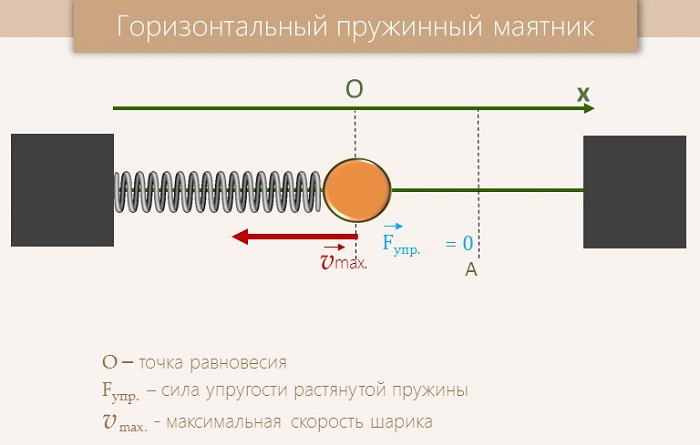
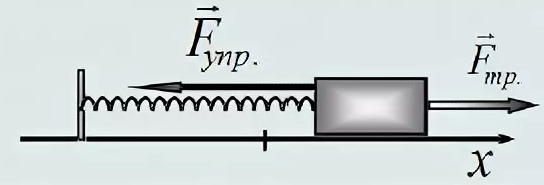
Рассмотрим простейший пружинный маятник — движущееся по горизонтальной плоскости твёрдое тело (груз), прикреплённое пружиной к стене (рис. (1)). Допустим, что силы трения не оказывают существенного влияния на движение груза.
Первоначально пружина не деформирована (не растянута и не сжата), поэтому никакие силы в горизонтальном направлении на груз не действуют. Точка О — положение равновесия груза.
Переместим груз вправо. Пружина при этом растянется, и в ней возникнет сила упругости, направленная влево, к положению равновесия, и по модулю равная:
где (x=A) — максимальное (амплитудное) отклонение груза от положения равновесия.
Если отпустить груз, то под действием силы упругости он начнёт ускоренно перемещаться влево, к точке (О), по мере приближения к которой скорость груза будет возрастать от нуля до некоторого максимального значения. При приближении к точке равновесия деформация пружины уменьшается, а значит, уменьшается и сила упругости. Так как груз имеет скорость при прохождении положения равновесия, то он по инерции продолжает свое движение влево. Теперь пружина начинает сжиматься (деформация сжатия), что приводит к возникновению силы упругости, направленной вправо, т.е. к положению равновесия. По мере возрастания степени деформации пружины сила растет и все больше тормозит движение груза. В конце концов, груз останавливается.
Но сила упругости, направленная к точке (О), будет продолжать действовать, поэтому груз вновь придёт в движение в обратную сторону, вправо, и на обратном пути его скорость будет возрастать от нуля до максимального значения в точке (О).
Движение груза от точки (О) к крайней правой точке снова приведёт к растяжению пружины, опять возникнет сила упругости, направленная к положению равновесия и замедляющая движение груза до полной его остановки.
Мы описали одно полное колебание.
В каждой точке траектории, кроме положения равновесия, на груз действует сила упругости пружины, которая направлена к положению равновесия.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
— ускорение пружинного маятника.
Обрати внимание!
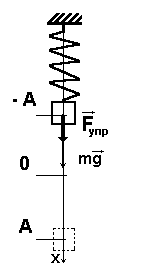
Данная формула справедлива и для вертикального пружинного маятника (рис. (2)) в котором действуют сила тяжести груза и сила упругости пружины.
Рис. (2). Колебания вертикального пружинного маятника
Обрати внимание!
Ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело. Сила тяжести только приводит к первоначальному изменению (смещению вниз) положения равновесия (рис. (3)).
Рис. (3). Изображение смещения маятника
Период свободных колебаний пружинного маятника определяется по формуле Гюйгенса:
(m) — масса груза,
(k) — коэффициент жёсткости пружины.
Пружинные маятники широко используются в качестве акселерометра в системах управления баллистических ракет, контактных взрывателях артиллерийских и авиационных боеприпасов и т. п.
Акселерометр (лат. accelero — «ускоряю» и др.-греч. μετρέω — «измеряю») — прибор, измеряющий проекцию кажущегося ускорения (разности между истинным ускорением объекта и гравитационным ускорением). Как правило, акселерометр представляет собой чувствительную массу, закреплённую в упругом подвесе. Отклонение массы от её первоначального положения при наличии кажущегося ускорения несёт информацию о величине этого ускорения.
Рис. (4). Схема акселерометра
На рисунке (4) — схема простейшего акселерометра. Груз закреплён на пружине. Демпфер подавляет колебания груза. Чем больше кажущееся ускорение, тем сильнее деформируется пружина, изменяя показания прибора.
Источники:
Рис. 1. Колебания пружинного маятника. © ЯКласс.
Рис. 2. Колебания вертикального пружинного маятника. © ЯКласс.
Рис. 3. Изображение смещения маятника.
Рис. 4. Схема акселерометра.
Содержание
-
1 Маятники
- 1.1 Пружинный маятник
- 1.2 Математический маятник
-
2 *Вывод формул
- 2.1 *Пружинный маятник
- 2.2 *Математический маятник
- 3 Литература
Маятники
Физическую систему (тело), в которой при отклонении от положения равновесия возникают и существуют колебания, называют колебательной системой.
Рассмотрим простейшие механические колебательные системы: пружинный и математический маятники.
Пружинный маятник
- Пружинный маятник — это колебательная система, состоящая из материальной точки массой m и пружины.
Различают горизонтальный пружинный маятник (рис. 1, а) и вертикальный (рис. 1, б).
а (исходник с сайта somit.ru)
<swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>Mex-majat-02.swf</swf>
б
Рис. 1.
Период колебаний пружинного маятника можно найти по формуле
(T=2pi cdot sqrt{frac{m}{k}},)
где k — коэффициент жесткости пружины маятника. Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды колебаний (в пределах выполнимости закона Гука).
- Свойство независимости периода колебаний маятника от амплитуды, открытое Галилеем, называется изохронностью (от греческих слов ίσος — равный и χρόνος —время).
Математический маятник
Рассмотрим простой маятник — шарик, подвешенный на длинной прочной нити. Такой маятник называется физический.
Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Если масса нити во много раз меньше массы шарика, то массой нити также можно пренебречь. В этом случае мы получаем модель маятника, которая называется математическим маятником.
- Математическим маятником называется, материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле силы тяжести (или других сил) (рис. 2).
<swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>Mex-majat-03.swf</swf>
Рис. 2.
Галилео Галилей экспериментально установил, что период колебаний математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения). Он установил также, что период колебаний прямо пропорционален (sqrt{l}).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса:
(T=2pi cdot sqrt{frac{l}{g}}.)
При углах отклонения математического маятника α < 20° погрешность расчета периода по формуле Гюйгенса не превышает 1%.
В общем случае, когда маятник находится в однородных полях нескольких сил, то для определения периода колебаний следует ввести «эффективное ускорение» g*, характеризующее результирующее действие этих полей и период колебаний маятника будет определяться по формуле
(T=2pi cdot sqrt{frac{l}{g*}}.)
*Вывод формул
*Пружинный маятник
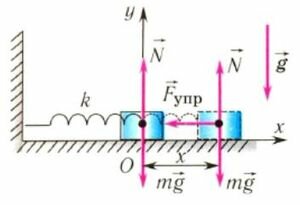
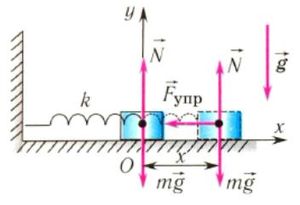
На груз m горизонтального пружинного маятника действуют сила тяжести (m⋅g), сила реакции опоры (N) и сила упругости пружины (Fynp) (рис. 3, первый две силы на рис. а не указаны). Запишем второй закон Ньютона для случая, изображенного на рис. 3, б
(mcdot vec{a} = vec{F}_{ynp} + mcdot vec{g}+vec{N},)
0Х[mcdot a_{x} = -F_{ynp} = -kcdot x] или (mcdot a_{x} +kcdot x=0.)
<swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>mex-majat-05.swf</swf>
а (материал с сайта science.up-life.ru)
Рис. 3.
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора
(a_{x} + frac{k}{m} cdot x = 0.)
Сравнивая полученное выражение с уравнением гармонических колебаний
(a_{x} (t) + omega^{2} cdot x(t) = 0,)
находим циклическую частоту колебаний пружинного маятника
(omega = sqrt{frac{k}{m}}.)
Тогда период колебаний пружинного маятника будет равен:
(T=frac{2pi }{omega } = 2pi cdot sqrt{frac{m}{k}}.)
*Математический маятник
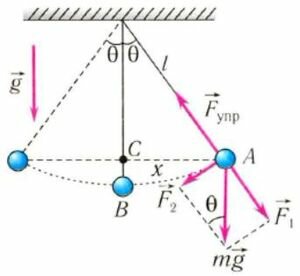
На груз m математического маятника действуют сила тяжести (m⋅g) и сила упругости нити (Fynp) (сила натяжения) (рис. 4). Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для случая, изображенного на рис. 4, б
(mcdot vec{a} = vec{F}_{ynp} + mcdot vec{g},)
(0X: mcdot a_{x} = -mcdot g cdot sin theta.)
<swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>mex-majat-04.swf</swf>
а (материал с сайта science.up-life.ru)
Рис. 4.
Пусть x — длина дуги AB, следовательно, x = l⋅θ, где угол θ выражен в радианах. Заметим, что при малых углах θ
(sin theta =theta =frac{x}{l}.)
Тогда
(mcdot a_{x} = -mcdot gcdot frac{x}{l}) или (a_{x} +frac{g}{l} cdot x=0.)
Сравнивая полученное выражение с уравнением гармонических колебаний
(a_{x} (t) + omega^{2} cdot x(t) = 0,)
находим, что при малых отклонениях маятник совершает гармонические колебания с циклической частотой
(omega =sqrt{frac{g}{l}}.)
Тогда период колебаний маятника будет равен:
(T = frac{2pi }{omega } =2pi cdot sqrt{frac{l}{g}}.)
Литература
- Жилко, В.В. Физика: учеб. Пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В.Жилко, Л.Г.Маркович. — Минск: Нар. Асвета, 2009. — С. 11-14.
Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается
Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.
Давайте выведем формулу периода пружинного маятника.
На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :
Все проецируем на ось ОХ:
Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:
Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
Тогда период колебаний пружинного маятника будет равен:
Так же есть:
Период математического маятника
Период физического маятника
Период крутильного маятника
В Формуле мы использовали :
— Период пружинного маятника маятника
— Масса груза
— Изменение длины пружины
— Коэффициент упругости пружины
— Ускорение свободного падения
— Циклическая частота пружинного маятника
— Сила реакции опоры
— Сила упругости