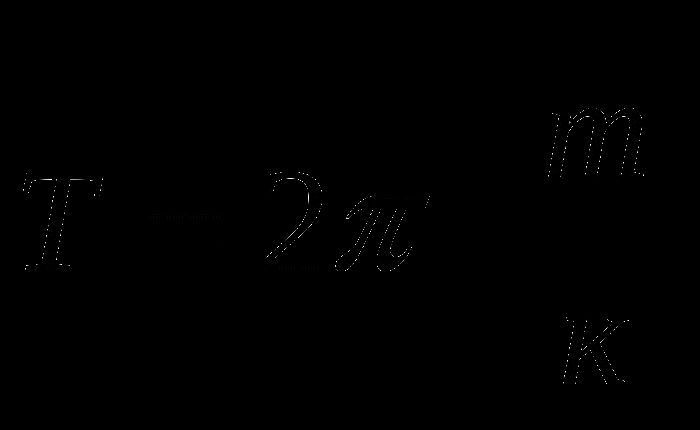Формула периода колебаний пружинного маятника в физике
Формула периода колебаний пружинного маятника
Определение
Период — это минимальное время, за которое совершается одно полное колебательное движение.
Обозначают период буквой $T$.
[T=frac{Delta t}{N}left(1right),]
где $Delta t$ — время колебаний; $N$ — число полных колебаний.
Уравнение колебаний пружинного маятника
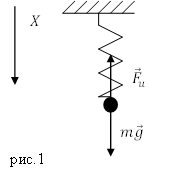
Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.
Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:
[mg=kb left(2right).]
Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
[F_u=-kleft(x+bright)left(3right).]
Ускорение груза запишем, помня, что движение происходит по оси X, как:
[a=frac{d^2x}{dt^2}=ddot{x }left(4right).]
Второй закон Ньютона для груза принимает вид:
[mddot{x}=-kleft(x+bright)+mg left(5right).]
Учтем равенство (2), формулу (5) преобразуем к виду:
[mddot{x}=-kx-kb+mg=-kx-mg+mg=-kx left(6right).]
Если ввести обозначение: ${omega }^2_0=frac{k}{m}$, то уравнение колебаний запишем как:
[ddot{x}+{omega }^2_0x=0left(7right),]
где ${omega }^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(8right),]
где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.
Формулы периода колебаний пружинного маятника
Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний.
Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($nu $):
[T=frac{1}{nu }left(9right).]
Период связан с циклической частотой колебаний как:
[T=frac{2pi }{{omega }_0}left(10right).]
Выше мы получали для пружинного маятника ${omega }_0=sqrt{frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:
[T=2pi sqrt{frac{m}{k}} left(11right).]
Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Примеры задач на период колебаний
Пример 1
Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?
Решение. Так как период — это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:
[T=frac{Delta t}{N}left(1.1right).]
Вычислим период:
[T=frac{10}{50}=0,2 left(сright).]
Частота — величина обратная периоду, следовательно:
[nu =frac{1}{T}left(1.2right).]
Вычислим частоту колебаний:
[nu =frac{1}{0,2}=5 left(Гцright).]
Ответ. $1) T=0,2$ с; 2) 5Гц
Пример 2
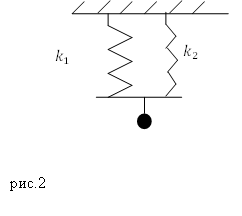
Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?
Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:
[T=2pi sqrt{frac{M}{k}} left(2.1right).]
При параллельном соединении пружин результирующая жесткость системы находится как:
[k=k_1{+k}_2left(2.2right).]
Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
[T=2pi sqrt{frac{M}{k_1{+k}_2}}.]
Ответ. $T=2pi sqrt{frac{M}{k_1{+k}_2}}$
Читать дальше: формула плеча силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
— амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий — по начальным значениям координаты и скорости.
к оглавлению ▴
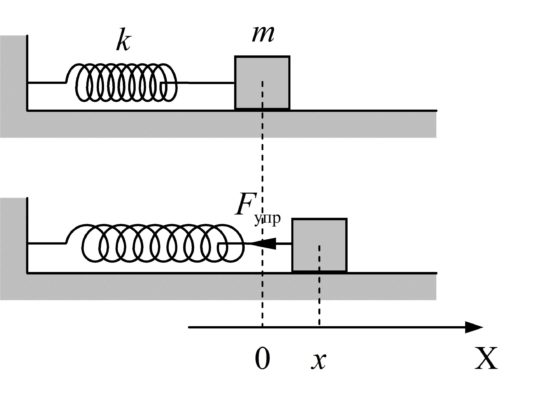
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Механическая колебательная система, состоящая из пружины с коэффициентом упругости (жёсткостью) (k), один конец которой жёстко закреплён, а на втором находится груз массы (m), называется пружинным маятником.
Рис. (1). Колебания пружинного маятника
Рассмотрим простейший пружинный маятник — движущееся по горизонтальной плоскости твёрдое тело (груз), прикреплённое пружиной к стене (рис. (1)). Допустим, что силы трения не оказывают существенного влияния на движение груза.
Первоначально пружина не деформирована (не растянута и не сжата), поэтому никакие силы в горизонтальном направлении на груз не действуют. Точка О — положение равновесия груза.
Переместим груз вправо. Пружина при этом растянется, и в ней возникнет сила упругости, направленная влево, к положению равновесия, и по модулю равная:
где (x=A) — максимальное (амплитудное) отклонение груза от положения равновесия.
Если отпустить груз, то под действием силы упругости он начнёт ускоренно перемещаться влево, к точке (О), по мере приближения к которой скорость груза будет возрастать от нуля до некоторого максимального значения. При приближении к точке равновесия деформация пружины уменьшается, а значит, уменьшается и сила упругости. Так как груз имеет скорость при прохождении положения равновесия, то он по инерции продолжает свое движение влево. Теперь пружина начинает сжиматься (деформация сжатия), что приводит к возникновению силы упругости, направленной вправо, т.е. к положению равновесия. По мере возрастания степени деформации пружины сила растет и все больше тормозит движение груза. В конце концов, груз останавливается.
Но сила упругости, направленная к точке (О), будет продолжать действовать, поэтому груз вновь придёт в движение в обратную сторону, вправо, и на обратном пути его скорость будет возрастать от нуля до максимального значения в точке (О).
Движение груза от точки (О) к крайней правой точке снова приведёт к растяжению пружины, опять возникнет сила упругости, направленная к положению равновесия и замедляющая движение груза до полной его остановки.
Мы описали одно полное колебание.
В каждой точке траектории, кроме положения равновесия, на груз действует сила упругости пружины, которая направлена к положению равновесия.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
— ускорение пружинного маятника.
Обрати внимание!
Данная формула справедлива и для вертикального пружинного маятника (рис. (2)) в котором действуют сила тяжести груза и сила упругости пружины.
Рис. (2). Колебания вертикального пружинного маятника
Обрати внимание!
Ускорение тела, колеблющегося на пружине, не зависит от силы тяжести, действующей на это тело. Сила тяжести только приводит к первоначальному изменению (смещению вниз) положения равновесия (рис. (3)).
Рис. (3). Изображение смещения маятника
Период свободных колебаний пружинного маятника определяется по формуле Гюйгенса:
(m) — масса груза,
(k) — коэффициент жёсткости пружины.
Пружинные маятники широко используются в качестве акселерометра в системах управления баллистических ракет, контактных взрывателях артиллерийских и авиационных боеприпасов и т. п.
Акселерометр (лат. accelero — «ускоряю» и др.-греч. μετρέω — «измеряю») — прибор, измеряющий проекцию кажущегося ускорения (разности между истинным ускорением объекта и гравитационным ускорением). Как правило, акселерометр представляет собой чувствительную массу, закреплённую в упругом подвесе. Отклонение массы от её первоначального положения при наличии кажущегося ускорения несёт информацию о величине этого ускорения.
Рис. (4). Схема акселерометра
На рисунке (4) — схема простейшего акселерометра. Груз закреплён на пружине. Демпфер подавляет колебания груза. Чем больше кажущееся ускорение, тем сильнее деформируется пружина, изменяя показания прибора.
Источники:
Рис. 1. Колебания пружинного маятника. © ЯКласс.
Рис. 2. Колебания вертикального пружинного маятника. © ЯКласс.
Рис. 3. Изображение смещения маятника.
Рис. 4. Схема акселерометра.
План урока:
Колебательное движение
Период и частота колебаний
Свободные колебания
Амплитуда колебаний
Колебательные системы
Гармонические колебания
Величины, характеризующие колебательное движение
Затухающие колебания
Вынужденные колебания
Колебательное движение
В самом широком смысле, колебательное движение – это любое движение, повторяющееся с течением времени. Например, птица, машущая крыльями вверх-вниз, совершает ими колебательные движения. Ребенок, качающийся на качелях, тоже совершает колебательные движения. Игла швейной машины при шитье – тоже.
Но как же так, ведь в названных примерах тела движутся абсолютно по-разному? Крылья птицы и игла швейной машины движутся вертикально вверх-вниз (прямолинейно), ребенок на качелях движется горизонтально и по дуге (криволинейно). Это все неважно. Главный признак колебательного движения – его повторяемость через определенный промежуток времени, то есть через период колебаний.
Период и частота колебаний
Период колебаний (T) – это время, за которое тело совершает полный цикл движения, т.е. совершает одно колебание.
В случае с движением крыльев птицы, если считать, что один взмах начинается с верхней точки, полным колебанием будет считаться, когда крылья пройдут от верхней точки через середину до нижней и вернутся от нижней точки через середину до верхней (рисунок 1).
Рисунок 1 – Взмах крыльев птицы как пример полного колебания
Период колебаний обозначается латинской буквой T. По определению период – это время, значит, единица измерения периода будет такой же, как и единица измерения времени. В СИ это секунда.
[T] = 1 с
Как же можно вычислить период колебаний?
Самый простой способ – это посчитать количество колебаний и секундомером измерить время, за которое эти колебания были совершены. Например, ребенок на качелях совершает N = 10 колебаний за t = 30 секунд. Нетрудно подсчитать, что время совершения одного полного колебания будет 30/10 = 3 с. Если обобщить, получится формула для нахождения периода колебаний:
где t – время, за которое совершено N колебаний.
Рассмотрим еще одну важную характеристику.
Частота колебаний (ν) – это количество колебаний, совершаемое телом за единицу времени.
Частота колебаний обозначается греческой буквой (читается как «ню»).
Если сравнить определение частоты колебаний с определением периода, можно заметить, что это обратные величины. То есть:
Гц – единица измерения, которую назвали в честь немецкого физика Генриха Герца. При решении задач одинаково часто употребляется и герц, и с-1. Можно употреблять и то, и другое – в зависимости от того, что удобнее при решении конкретной задачи.
Следует так же отметить, что иногда физики пользуются циклической частотой колебаний:
Свободные колебания
Положение равновесия при колебательном движении
Сравним две ситуации:
1. Родитель толкает качели, на которых сидит ребенок, а потом просто наблюдает, как качели качаются сами по себе.
2. Родитель толкает качели с ребенком, а потом при каждом цикле движения подталкивает качели, поддерживая качания.
Физики говорят, что в первом случае система (качели и ребенок) совершает свободные колебания, то есть колебания под действием только внутренних сил. После выведения системы из равновесия (то есть толчка родителя) к ней больше не прикладывают внешних сил. Во втором случае говорят, что система совершает вынужденные колебания – то есть колебания, под действием периодического внешнего воздействия.
Поговорим о свободных колебаниях. Для простоты рассмотрим систему, состоящую из маленького тяжелого шарика на длинной крепкой нити. Такая система называется нитяным маятником (рисунок 2).
Рис.2 – Нитяной маятник
Без воздействия внешних сил шарик будет находиться в положении 1. Такое состояние называется положением равновесия. Далее к шарику прикладывают силу, направленную влево и он начинает совершать колебания. Траектория шарика будет: 1-2-1-3-1 (см. рисунок 1).
Как при этом будет меняться скорость тела? Для того, чтобы рассмотреть подробно, нужно помнить определения потенциальной и кинетической энергии*, а также в чем заключается закон сохранения энергии (систему считаем замкнутой – потерь энергии не происходит, а, значит, закон сохранения энергии выполняется – энергия колебательной системы остается постоянной):
- при движении из точки 1 в 2 шарик постепенно замедляется (уменьшается его кинетическая энергия, а потенциальная увеличивается);
- в точке 2 он на мгновенье останавливается (кинетическая энергия равна нулю, потенциальная максимальна);
- далее он начинает движение с ускорением, но уже в обратном направлении (кинетическая энергия увеличивается, потенциальная уменьшается) — при движении из 2 в 1 тело будет ускоряться;
- когда шарик дойдет до точки 1 его кинетическая энергия будет максимальна, а потенциальная минимальна.
При движении от точки 1 в 3 будет происходить то же самое, что и при движении из 1 в 2 – предлагаем описать процесс изменения величин (скорости и энергии) самостоятельно.
Если обобщить все сказанное, можно сделать вывод: при колебаниях в положении равновесия кинетическая энергия тела максимальна, а потенциальная минимальна (или равна нулю, в зависимости от выбранной точки отсчета). В крайних положениях потенциальная энергия максимальна, а кинетическая равна нулю. То есть положение равновесия маятника – это такое положение, в котором его потенциальная энергия минимальна (или равна нулю, в зависимости от точки отсчета). При удалении маятника от положения равновесия кинетическая энергия будет уменьшаться, а потенциальная увеличиваться.
*Потенциальная энергия тела зависит от его положения в пространстве; кроме того, это относительная величина – она зависит от того, какая точка отсчета выбрана.
Кинетическая энергия зависит от модуля скорости тела.
Амплитуда колебаний
Помимо частоты и периода важной характеристикой колебаний является амплитуда.
Амплитуда колебаний – это модуль максимального смещения тела от положения равновесия. Другими словами, это расстояние между положением равновесия и крайней точкой траектории маятника. Рассмотрим рисунок 3. На нем изображен уже знакомый вам нитяной маятник. В идеальном случае амплитуду колебаний маятника нужно считать как длину дуги от положения равновесия до крайней точки. Но если мы считаем, что колебания малые – то есть длина нити маятника (l) гораздо больше смещения (S), можно считать, что длина дуги совпадает с длиной отрезка между проекциями положения равновесия и крайней точки на ось ОХ.
Рис.3 – Амплитуда колебаний нитяного маятника
Обычно амплитуда обозначается большой латинской буквой A.
Колебательные системы
Для того, чтобы рассмотреть колебательные движения подробнее, рассмотрим несколько колебательных систем, на примере которых будет рассматривать все закономерности.
1. Маятник
В общем случае маятник – это система, способная совершать колебания под действием каких-либо сил, например, сил трения, упругости, тяжести.
2. Пружинный маятник
Пружинный маятник – это система, состоящая из упругой пружины, один конец которой закреплен, а на другой прикреплен груз.
Такой маятник может быть вертикальным (рисунок 4а), тогда колебания будут совершаться под действием сил тяжести и упругости; и горизонтальным (рисунок 4б), тогда на груз будут действовать сил упругости и трения.
Рис.4 – Пружинный маятник
Для пружинного маятника справедливы формулы:
где T –период колебаний пружинного маятника; π ~ 3.14; m–масса груза;k–коэффициент жесткости пружины; — частота колебаний пружинного маятника.
*Ранее говорилось, что существует такая характеристика, как циклическая частота. Формула для ее нахождения будет выглядеть так:
3. Нитяной маятник
Этот вид маятника уже рассматривался ранее (см. рисунок 3), он состоит из длинной нити и тяжелого грузика, подвешенного на ней.
Для нитяного маятника справедливы формулы:
где T – период колебаний нитяного маятника; π ~ 3.14; l –длина нити; g – ускорение свободного падения (~9,8 м/с2), v — частота колебаний.
Интересно отметить, что период нитяного маятника и, следовательно, его частота не зависят от массы грузика, прикрепленного к нити.
*Следует отметить, что все приведенные формулы справедливы только для малых колебаний.
** Циклическая частота нитяного маятника:
Гармонические колебания
При решении задач часто используется не нитяной маятник, а его упрощенная модель – математический маятник. Это идеальная колебательная система, в которой нить считается очень длинной по сравнению с амплитудой колебаний и размерами грузика; сам груз достаточно тяжелым, чтобы пренебречь массой нити. Кроме того, считается, что не происходит потерь энергии.
Рассмотрим подробно, какие силы действуют на такую систему. В первую очередь, на грузик действует сила тяжести mg, направленная вниз (см. рисунок 5). Так же на него действует сила натяжения со стороны нити F, она направлена вдоль нити. Обозначим угол, на который смещается тело от положения равновесия.
Рис.5 – Силы, действующие на математический маятник
Запишем 2-й закон Ньютона:
Рисунок 6 – Силы, действующие на математический маятник при смещении на угол φ
В случае малых углов sinφ можно считать равным φ. Из геометрического определения синуса:
Тогда в крайней точке 2-й закон Ньютона в проекции на ось OX перепишется следующим образом:
То есть ускорение, с которым движется маятник прямо пропорционально его смещению от положения равновесия. Минус в данном выражении означает, что ускорении направлено в противоположную сторону от смещения.
Интересно заметить, что ускорение грузика, подвешенного к ниточке (а значит и самого маятника), не зависит от его массы. Период колебаний математического маятника тоже не зависит от массы грузика:
В случаях, когда колебания происходят под действием силы, пропорциональной смещению тела от положения равновесия, говорят, что тело совершает гармонические колебания.*
График зависимости смещения от времени при гармоническом колебательном движении представляет собой синусоиду или косинусоиду (см. рисунок 7).
Для лучшего понимания, почему график выглядит именно так, можно посмотреть урок в курсе алгебры «Тригонометрические функции»:
Рис. 7 – График зависимости смещения (x) от времени (t) при гармонических колебаниях
На графическом представлении колебаний (рисунок 7) удобно находить период и амплитуду гармонических колебаний.
*Могло сложиться впечатление, что гармонические колебания может совершать только математический маятник. Это не так. Любое тело может совершать колебания, близкие к гармоническим (нужно учитывать не идеальность систем). Например, можно говорить о гармонических колебаниях пружины, если она достаточно жесткая, чтобы она деформировалась упруго, а колебания совершаются с небольшой амплитудой.
Величины, характеризующие колебательное движение
Ранее рассматривались такие характеристики колебаний, как период, частота и амплитуда. Помимо этих величин, колебания характеризуются фазой колебаний.
Фаза колебаний
На рисунке 7 изображен график зависимости смещения от времени при гармонических колебаниях. Такой график называется синусоидой (косинусоидой). В общем случае уравнение зависимости координаты Х от времени t будет выглядеть так:
Разность фаз
Понятие «разность фаз» применяется, когда мы хотим сравнить движение двух маятников. Пусть маятник 1 и маятник 2 двигаются по законам соответственно:
Найдем разность фаз колебаний этих двух маятников.
Если взять конкретный момент времени , фаза гармонических колебаний каждого из маятников в этот момент времени будет:

Затухающие колебания
Во всех рассмотренных ранее случаях считалось, что на колеблющуюся систему не действуют силы извне. На самом деле, идеальных систем не существует, поэтому любой маятник во время движения будет преодолевать внешние силы сопротивления и терять энергию. Например, пружинный маятник (рисунок 
Рисунок 8 – Пружинный маятник на шероховатой поверхности
Колебания, энергия которых уменьшается с течением времени, называются затухающими.
Амплитуда затухающих колебаний уменьшается со временем. График таких колебаний изображен на рисунке 9.
Рисунок 9 – График зависимости координаты от времени при затухающих колебаниях
Вынужденные колебания
Собственная частота колебаний. Частота вынуждающей силы. Установившиеся вынужденные колебания
В реальных (неидеальных) системах колебания всегда нужно поддерживать внешним воздействием.
Под действием периодической внешней изменяющейся силы возникают вынужденные колебания.
Почему же обязательно сила должны быть периодически изменяющейся? Ответ на этот вопрос легко найти, представив себе качели. Если на них действовать с постоянной по модулю и направлению силой, они никогда не начнут качаться. А толчками (то есть периодической изменяющейся силой) раскачать их не составит труда.
Внешняя сила, заставляющая систему совершать колебания, называется вынуждающей силой.
Так как эта сила периодическая, необходимо ввести частоту вынуждающей силы. А чтобы не запутаться, частоту свободных колебаний называют собственной частотой системы. Как показывают эксперименты, даже если изначально собственная частота системы и частота вынуждающей силы отличались, через некоторое время система начинает колебаться с частотой вынуждающей силы. В таких случаях говорят об установившихся вынужденных колебаниях.
Если частота вынуждающей силы равна собственной частоте системы, возникает резонанс – резкое увеличение амплитуды колебаний.
Период колебаний пружинного маятника

4.7
Средняя оценка: 4.7
Всего получено оценок: 87.
4.7
Средняя оценка: 4.7
Всего получено оценок: 87.
Одной из простейших колебательных систем, удобных для изучения, является пружинный маятник. Рассмотрим его подробнее, получим формулу периода колебаний.
Пружинный маятник
Идеальный пружинный маятник представляет собой некоторую точечную массу $m$, которая закреплена на одном конце пружины с постоянной жесткостью $k$, а другой конец пружины – закреплен к неподвижной опоре. Больше никакие силы на пружинный маятник не действуют, и он способен к совершению свободных незатухающих колебаний.
Уравнение движения пружинного маятника
Пусть начало координат находится в точке покоя маятника. Тогда, если маятник выведен из состояния равновесия на расстояние $x$, со стороны пружины на него начинает действовать сила $F=-kx$.
Знак «минус» означает, что направление действия этой силы противоположно смещению маятника.
Согласно второму закону Ньютона, если на тело действует сила, то оно приобретает ускорение:
$$a=-{kxover m}$$
Скорость – это производная координаты. А ускорение – производная скорости. Следовательно, ускорение – это вторая производная координаты. Получим уравнение:
$$x”=-{kover m}x$$
То есть, вторая производная координаты пропорциональна самой координате, взятой с противоположным знаком. Это дифференциальное уравнение, и в высшей математике доказывается, что единственная функция, являющаяся его решением – это круговая функця (синус или косинус).
Полное же решение данного уравнения выглядит следующим образом:
$$x(t)=A cos sqrt{kover m}t$$
Если взять вторую производную этой функции, то можно убедиться, что она равна самой себе, с противоположным знаком и необходимым коэффициентом.
Период колебаний маятника
Сравним полученное уравнение с уравнением гармонических колебаний:
$$x(t)=A cos( omega t+varphi)$$
Можно видеть, что фаза $varphi$ в уравнении координаты движения маятника равна нулю, а коэффициент $sqrt {kover m}$ представляет собой круговую частоту. Учитывая формулу, связывающей круговую частоту и период, получим формулу периода колебаний пружинного маятника:
$$T={2pi over omega}=2pisqrt {mover k}$$
Действительно, чем больше масса пружинного маятника, тем дольше будут совершаться колебания. А чем больше жесткость пружины, тем период колебаний будет меньше. Но величины эти связаны с периодом не прямо, а через коренную зависимость, то есть, для увеличения периода маятника вдвое, надо либо увеличить массу маятника вчетверо, либо во столько же раз уменьшить жесткость пружины.
В реальности на маятник всегда действует сила тяжести, кроме того, в нем происходят потери, связанные с трением и нагревом пружины. Поэтому, его колебания будут затухающими, а их период будет немного отличаться от расчетного. Наиболее близким к идеальному пружинному маятнику является механизм часового балансира.
Что мы узнали?
Пружинный маятник – это точечная масса, двигающая под воздействием пружины постоянной жесткости. Период колебаний пружинного маятника пропорционален корню из отношения его массы к жесткости пружины.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 87.
А какая ваша оценка?