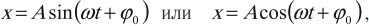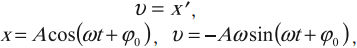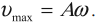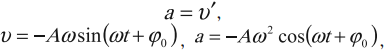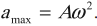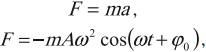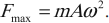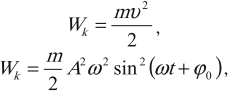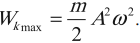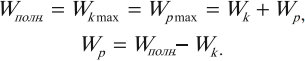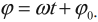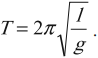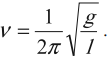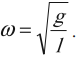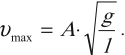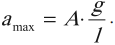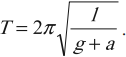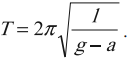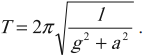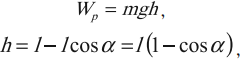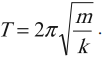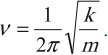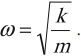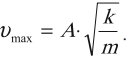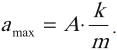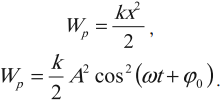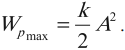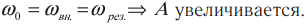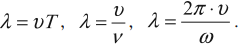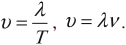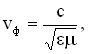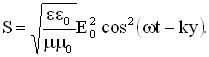Отдельные частицы любого тела — твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-то частица начинает колебаться, то благодаря взаимодействию между частицами это движение с некоторой скоростью начинает распространяться во все стороны.
Определение
Волна — колебания, распространяющиеся в пространстве с течение времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря силам упругости. Эти силы осуществляют связь между отдельными частями тела. В образовании волн на поверхности воды играют роль сила тяжести и сила поверхностного натяжения. Такие волны позволяют наиболее наглядно рассмотреть главные особенности волнового движения.
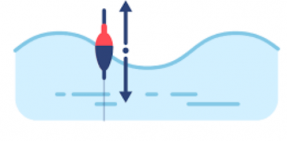
Волна на поверхности воды представляет собой бегущие вперед валы округлой формы. Расстояние между валами, которые также называют гребнями, примерно одинаковы. Волны распространяются в среде с определенной скоростью. Так, если чайка летит вперед, а по ней в любой момент времени оказывается один и тот же гребень, то скорость распространения волны можно принять равной скорости полета чайки. Волны на воде наблюдать удобно потому, что скорость их распространения невелика.
Если бросить в воду легкий предмет, он не будет увлекаться волной, а начнет совершать колебания вверх и вниз, оставаясь примерно на одном месте, как поплавок. Это говорит о том, что частицы воды остаются на месте в то время, как волна распространяется на большие расстояния.
Если же резко толкнуть горизонтальную пружину, можно будет наблюдать, как в одних местах она разрежается, в других — уплотняется. Это тоже волна. Видно, что энергия, полученная от толчка руки, переносится через пружину, хотя ее частицы остаются на месте.
Примеры с поплавком на воде и горизонтальной пружиной позволяют сделать вывод, что волна переносит энергию, но не переносит вещество среды.
Виды механических волн
По характеру колебаний частиц среды относительно положения равновесия различают два вида волн:
Определения
- Поперечная волна — волна, при которой частицы среды колеблются перпендикулярно направлению распространения этой волны.
- Продольная волна — волна, при которой частицы среды колеблются параллельно направлению распространения этой волны.
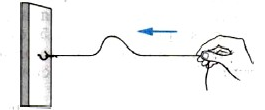
Волны, распространяющиеся вдоль резинового шнура, являются поперечными (см. рисунок ниже). Чтобы появилась волна, нужно взять конец шнура, прикрепленного к вертикальной опоре, и дернуть его. При этом волна побежит к вертикальной опоре, а сам шнур будет менять свою форму. Каждая частица шнура станет совершать колебания относительно своего неизмененного положения равновесия сверху вниз (перпендикулярно направлению распространения волны).
Рассмотрим поперечные волны подробнее. Каждый участок шнура обладает массой и упругостью. При деформации шнура в любом его сечении появляются силы упругости. Эти силы стремятся возвратить шнур в исходное положение. Благодаря инертности участок колеблющегося шнура не останавливается в положении равновесия, а проходит его, продолжая двигаться до тех пор, пока силы упругости не остановят этот участок в момент максимального отклонения от положения равновесия.
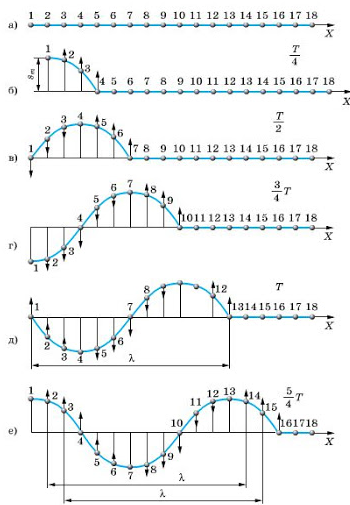
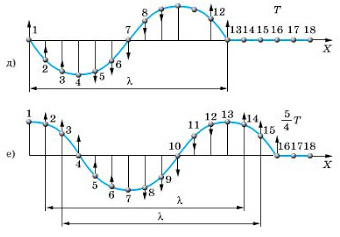
На рисунках а, б, в, г, д и е изображен процесс распространения поперечной волны. На них показаны положения частиц среды в последовательные моменты времени.
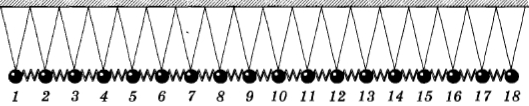
Теперь рассмотрим распространение в среде продольной волны. Такую волну можно наблюдать, собрав установку из цепочки массивных шариков, связанных пружинками. Шары подвешены так, чтобы они могли колебаться только вдоль цепочки (см. рисунок ниже).
Если первый шар привести в колебательное движение, то вдоль цепочки побежит продольная волна, состоящая из чередующихся уплотнений и разрежений шаров. Уплотнения и разрежения (см. рисунок ниже) появляются вследствие горизонтальных колебаний шаров у положения равновесия. Волна также распространяется горизонтально.
Физические характеристики волны
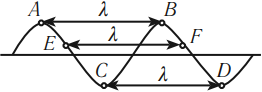
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Определение
Длина волны — расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ2, колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
v=λT
Но мы знаем, что период равен величине, обратной частоте колебаний:
T=1ν
Тогда скорость распространения волны равна:
v=λν
Скорость волны равна произведению длины волны на частоту колебаний.
При распространении волны мы имеем дело с периодичностью двоякого рода:
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
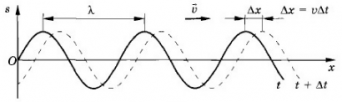
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
ν=nt
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v=λν=λnt=1·105=2 (мс)
Уравнение бегущей волны
Определение
Бегущая волна — волна, распространяющаяся в пространстве.
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
s = s(x, t)
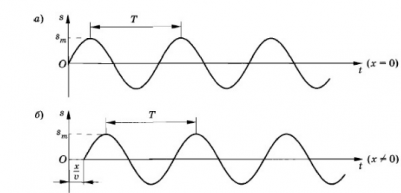
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = smaxsin ωt
smax — амплитуда колебаний (рис. а).
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
τ=xv
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Уравнение бегущей волны
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s(x, t)=0,1sin(2πt−xπ2). Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω=2π (радс)
v=4 (мс)
Циклическую частоту также можно рассчитать по формуле:
ω=2πν
Тогда частота волны равна:
ν=ω2π=2π2π=1 (Гц)
Тогда длина волны равна:
λ=vν=41=4 (м)
Задание EF18242
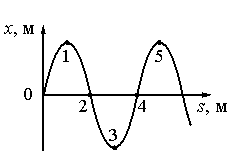
Ответ:
а) π/3
б) π/2
в) π
г) 2π
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу, которая связывает скорость волны с ее частотой и длиной.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Частота звуковой волны: ν = 400 Гц.
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν=4·400=1600 (мс)
Ответ: 1600
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18803
На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Расстояние наблюдателя до источника звука: s = 510 м.
Звук от удара проделает путь, равный одинарному расстоянию от наблюдателя до источника звука. Следовательно, для нахождения времени, через которое наблюдатель услышит звук, нужно разделить этот путь на скорость звука в воздухе:
t=sv=510340=1,5 (с)
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.1k
КОЛЕБАНИЯ И ВОЛНЫ
Колебания
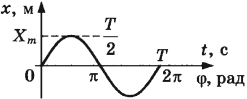
Механические колебания — периодически повторяющиеся изменения положения тела (материальной точки) относительно положения равновесия.
Амплитуда — максимальное отклонение тела от положения равновесия.
Период — время за которое совершается одно полное колебание. Единица измерения секунда (с).
Частота — количество колебаний
в единицу времени
. Измеряется частота в герцах (Гц) показывающих количество колебаний за секунду. К примеру величина 50 Гц говорит нам о том, что система за одну секунду совершила 50 колебаний.
Так как период это время за которое совершается одно полное колебание, можно выразить частоту следующим образом:
Гармонические колебания — колебания происходящие по законам синуса или косинуса (гармоническому закону).
Фаза колебания () — аргумент периодической функции, описывающей колебательный или волновой процесс.
Начальная фаза колебания — значение фазы колебаний в начальный момент времени, т.е. при t = 0.
Циклическая частота — скалярная физическая величина, мера частоты вращательного или колебательного движения. Единица измерения радиан в секунду (рад/с).
Исходя из этого можно записать
Свободные колебания — колебания возникающие за счет внутренних сил системы, после того как она была выведена из состояния равновесия.
Собственные частота колебаний — частота свободных колебаний колебательной системы.
Затухающие колебания — колебания в которых происходит постепенное уменьшение амплитуды в результате действия сил сопротивления движению (силы трения, силы сопротивления воздуха..).
Вынужденные колебания — колебания, происходящие под действием внешних периодически изменяющейся сил.
Резонанс — резкое увеличение амплитуды колебания при совпадении собственной частоты колебательной системы, с частотой вынуждающей силы.
Математический маятник
Математический маятник — механическая колебательная система представляющая из себя материальную точку подвешенную на нерастяжимой невесомой нити в поле силы тяжести.
Формула Гюгенса для определения периода колебаний математического маятника. l — длинна маятника.
Циклическая частота колебаний математического маятника.
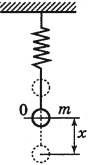
Пружинный маятник
Пружинный маятник — механическая колебательная система представляющая из себя пружину жесткостью , с материальной точкой массой
на одном конце этой пружины.
Колебательный контур
Электромагнитные колебания — периодические изменения напряжённости и магнитной индукции.
Колебательный контур — электрическая цепь, состоящая из конденсатора ёмкостью и катушки индуктивностью
. В этой цепи происходят свободные электромагнитные колебания.
Циклическая частота и период собственных колебаний контура определяются по формуле Томсона:
Связь между амплитудными (максимальными) значениями тока в контуре и заряда на конденсаторе:
Энергия контура:
Связь между амплитудными (максимальными) значениями тока и напряжения в контуре (закон сохранения энергии в колебательном контуре):
Переменный ток
Переменный ток — электрический ток периодически меняющий свое направление.
Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Действующее значение напряжения в цепи переменного тока равно напряжению постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
Средняя по времени тепловая мощность переменного тока:
Емкостное сопротивление — сопротивление конденсатора в цепи переменного тока. Емкостное сопротивление зависит от частоты переменного тока, чем частота выше, тем сопротивление ниже. Для постоянного тока конденсатор по сути представляет разрыв цепи, по этому для постоянного тока емкостное сопротивление стремиться к бесконечности.
Где циклическая частота переменного тока.
Закон Ома для участков цепи, содержащих емкость:
Индуктивное сопротивление — сопротивление катушки индуктивности в цепи переменного тока. Так как изменение тока в цепи приводит к появлению токов самоиндукции противодействующих этому изменению, то увеличение частоты переменного тока приводит к увеличению индукционного сопротивления.
Закон Ома для участков цепи, содержащих индуктивность:
Трансформатор
Трансформатор — электромагнитное устройство, которое используется для передачи и преобразования электрической энергии из одной катушки индуктивности на сердечнике в другую. Частота переменного тока при этом не меняется.
Идеальный трансформатор — трансформатор в котором энергетические потери пренебрежимо малы.
Отношение напряжений на вторичной и первичной
обмотках идеального трансформатора равно отношению количеств их витков. (
на вторичной и
первичной). Само это соотношение называют коэффициентом трансформации
.
Если коэффициент трансформации больше единицы, то трансформатор называется понижающим, если меньше, то повышающим.
Закон сохранения энергии для идеального трансформатора:
КПД неидеального трансформатора:
Волны
Волны — колебания распространяющийся в упругих средах. Если направление распространения волн и направление колеблющихся частиц среды совпадают то такие волны называются продольными. А если эти направления перпендикулярны друг другу, то такие волны называют поперечными.
Так как волновые процессы являются часным случаем колебательного движения, они так же будут характеризоваться своими частотой и периодом. Но помимо этого у волн есть еще свои дополнительные характеристики, отличающие их от обычного колебательного движения.
Длина волны — расстояние, на которое успевает распространиться волна за один период;
Скорость распространения волны — отношение длинны волны к периоду ее колебания.
Звуковые волны — разновидность механических волн в слышимом для человека диапазоне ( от 16 Гц до 20 кГц).
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
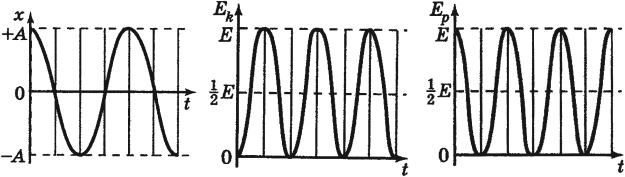
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
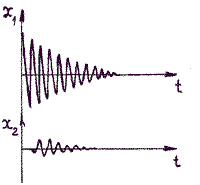
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
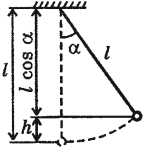
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
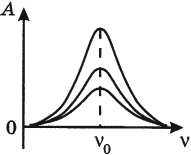
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
2.9 (58.68%) 152 votes
Гармонические колебания происходят по
закону:
x
= A
cos(ωt
+ φ0),
где
x
– смещение частицы от положения
равновесия, А
– амплитуда колебаний, ω – круговая
частота, φ0
– начальная фаза, t
– время.
Период
колебаний T
=
.
Скорость колеблющейся частицы:
υ
=
= – A
ω
sin (ωt
+ φ0),
ускорение
a
=
= –
Aω2
cos
(ωt
+ φ0).
Кинетическая энергия частицы, совершающей
колебательное движение: Ek
=
=
sin2(ωt+ φ0).
Потенциальная
энергия:
En
=
cos2(ωt
+ φ0).
Периоды колебаний маятников
– пружинного
T
=
,
где
m
– масса груза, k
– коэффициент жесткости пружины,
– математического
T
=
,
где
l
– длина
подвеса, g
– ускорение свободного падения,
– физического
T
=
,
где
I
– момент
инерции маятника относительно оси,
проходящей через точку подвеса, m
– масса маятника, l
– расстояние от точки подвеса до центра
масс.
Приведенная
длина физического маятника находится
из условия: lnp
=
,
обозначения те
же, что для физического маятника.
При сложении двух
гармонических колебаний одной частоты
и одного направления получается
гармоническое колебание той же частоты
с амплитудой:
A
= A12
+
A22
+
2A1
A2
cos(φ2
–
φ1)
и
начальной
фазой:
φ =
arctg
.
где
А1,
A2
– амплитуды, φ1,
φ2
– начальные фазы складываемых колебаний.
Траектория
результирующего движения при сложении
взаимноперпендикулярных колебаний
одной частоты:
+
–
cos
(φ2
– φ1)
= sin2
(φ2
– φ1).
Затухающие колебания происходят по
закону:
x
= A0
e—
βt
cos(ωt
+ φ0),
где
β – коэффициент затухания, смысл
остальных параметров тот же, что для
гармонических колебаний, А0
– начальная амплитуда. В момент времени
t
амплитуда колебаний:
A
= A0
e
— βt.
Логарифмическим
декрементом затухания называют:
λ
= ln
= βT,
где
Т
– период колебания: T
=
.
Добротностью колебательной системы
называют:
D
=
.
Уравнение плоской бегущей волны имеет
вид:
y
= y0
cos
ω(t
±
),
где
у
– смещение колеблющейся величины от
положения равновесия, у0
– амплитуда, ω – круговая частота, t
– время, х
– координата, вдоль которой распространяется
волна, υ
– скорость распространения волны.
Знак
«+» соответствует волне, распространяющейся
против оси X,
знак «–» соответствует волне,
распространяющейся по оси Х.
Длиной волны называют ее пространственный
период:
λ
= υT,
где
υ–скорость
распространения волны, T–период
распространяющихся колебаний.
Уравнение волны можно записать:
y
= y0
cos
2π
(+
).
Стоячая волна описывается уравнением:
y
= (2y0
cos
)
cos ωt.
В скобки заключена амплитуда стоячей
волны. Точки с максимальной амплитудой
называются пучностями,
xп
= n,
точки с нулевой
амплитудой – узлами,
xу
=
(n
+
)
.
Примеры решения задач
Задача
20
Амплитуда
гармонических колебаний равна 50 мм,
период 4 с и начальная фаза
.
а) Записать уравнение этого колебания;
б) найти смещения колеблющейся точки
от положения равновесия при t=0
и при t
= 1,5 с; в) начертить график этого движения.
Решение
Уравнение
колебания записывается в виде x
= a
cos(t
+
0).
По
условию известен период колебаний.
Через него можно выразить круговую
частоту
=
.
Остальные параметры известны:
а)
x
= 0,05 cos(t
+
).
б)
Смещение x
при t
=
0.
x1
= 0,05 cos=
0,05
=
0,0355 м.
При
t
=
1,5 c
x2
= 0,05 cos(1,5
+
)=
0,05 cos
=
– 0,05 м.
в
график функцииx=0,05cos
(t
+
)
выглядит следующим образом:
Определим
положение нескольких точек. Известны
х1(0)
и х2(1,5),
а также период колебаний. Значит, через
t
= 4 c
значение х
повторяется, а через t
=
2 c
меняет знак. Между максимумом и минимумом
посередине – 0 .
Задача
21
Точка
совершает гармоническое колебание.
Период колебаний 2 с, амплитуда 50 мм,
начальная фаза равна нулю. Найти скорость
точки в момент времени, когда ее смещение
от положения равновесия равно 25 мм.
Решение
1
способ. Записываем уравнение колебания
точки:
x
= 0,05 cos
t,
т.
к.
=
=.
Находим
скорость в момент времени t:
υ
=
= – 0,05
cos
t.
Находим
момент времени, когда смещение равно
0,025 м:
0,025
= 0,05 cos
t1,
отсюда
cos t1
=
,
t1
=
.Подставляем
это значение в выражение для скорости:
υ
= – 0,05
sin
=
–
0,05
=
0,136 м/c.
2
способ. Полная энергия колебательного
движения:
E
=
,
где
а
– амплитуда,
– круговая частота,
m
–
масса
частицы.
В
каждый момент времени она складывается
из потенциальной и кинетической энергии
точки
Ek
=
,
Eп
=
,
но k
= m2,
значит, Eп
=
.
Запишем
закон сохранения энергии:
=
+
,
отсюда
получаем: a22
=
υ
2 +
2x2,
υ
=
=
=
0,136 м/c.
Задача
22
Амплитуда
гармонических колебаний материальной
точки А
= 2 см, полная энергия Е
=
3∙10-7
Дж.
При каком смещении от положения равновесия
на колеблющуюся точку действует сила
F
=
2,25∙10-5
Н?
Решение
Полная
энергия точки, совершающей гармонические
колебания, равна:
E
=
.
(13)
Модуль
упругой силы выражается через смещение
точек от положения равновесия x
следующим образом:
F
= k
x
(14)
В
формулу (13) входят масса m
и круговая частота ,
а в (14) – коэффициент жесткости k.
Но круговая частота связана с m
и k:
2
=
,
отсюда
k
= m2
и F
= m2x.
Выразив m2
из
соотношения (13) получим:
m2
=
,
F
=
x.
Откуда
и получаем выражение для смещения x:
x
=
.
Подстановка
числовых значений дает:
x
=
= 1,5∙10-2
м
= 1,5 см.
Задача
23
Точка
участвует в двух колебаниях с одинаковыми
периодами и начальными фазами. Амплитуды
колебаний А1
=
3 см и А2
= 4 см. Найти амплитуду результирующего
колебания, если: 1) колебания происходят
в одном направлении; 2) колебания взаимно
перпендикулярны.
Решение
-
Если
колебания происходят в одном направлении,
то амплитуда результирующего колебания
определится как:
A
=
,
где
А1
и А2
– амплитуды складываемых колебаний,
1
и 2–начальные
фазы. По условию начальные фазы одинаковы,
значит 2
–
1
=
0, а cos
0 = 1.
Следовательно:
A
=
=
=
А1+А2
=
7 см.
-
Если
колебания взаимно перпендикулярны, то
уравнение результирующего движения
будет:
cos(
2
–
1)
= sin2(
2
–
1).
Так
как по условию 2
–
1
=
0, cos
0 = 1, sin
0 = 0, то уравнение запишется в виде:
=0,
или
=0,
или
.
Полученное
соотношение между x
и у
можно
изобразить на графике. Из графика видно,
что результирующим будет колебание
точки на прямой MN.
Амплитуда этого колебания определится
как:
A
=
=
5 см.
Задача
24
Период
затухающих колебаний Т=4
с, логарифмический декремент затухания
= 1,6 , начальная фаза равна нулю. Смещение
точки при t
=
равно 4,5 см. 1) Написать уравнение этого
колебания; 2) Построить график этого
движения для двух периодов.
Решение
-
Уравнение
затухающих колебаний с нулевой начальной
фазой имеет вид:
x
= A0e
—t
cos2.
Для
подстановки числовых значений не хватает
величин начальной амплитуды А0
и
коэффициента затухания .
Коэффициент
затухания можно определить из соотношения
для логарифмического декремента
затухания:
=
Т.
Таким
образом
=
=
= 0,4 с-1.
Начальную
амплитуду можно определить, подставив
второе условие:
4,5
см
= A0
cos
2= A0
cos
=A0
.
Отсюда
находим:
A0
=
4,5∙
(см)
= 7,75 см.
Окончательно
уравнение движения:
x
= 0,0775
cos
t.
-
Для
построения графика сначала рисуем
огибающую x
=
0,0775
,
а затем колебательную часть.
Задача
25
Чему
равен логарифмический декремент
затухания математического маятника,
если за t
=
1 мин амплитуда колебаний уменьшилась
в два раза? Длина маятника l
=
1 м.
Решение
Логарифмический
декремент затухания можно найти из
соотношения: =
Т,
где
– коэффициент затухания, Т
– период колебаний. Собственная круговая
частота математического маятника:
0
=
= 3,13 с-1.
Коэффициент
затухания колебаний можно определить
из условия:
A0
=
A0
e—t,
t
= ln2
= 0,693 ,
=
= 0,0116c-1.
Поскольку
<< 0,
то
в формуле
=
можно пренебречь
по сравнению с 0
и
период
колебаний определить по формуле:
T
=
= 2c.
Подставляем
и Т
в выражение для логарифмического
декремента затухания и получаем:
=
T
= 0,0116 с-1
∙ 2 с = 0,0232.
Задача
26
Уравнение
незатухающих
колебаний
дано
в виде
x
=
4
sin600
t
см.
Найти
смещение от положения равновесия точки,
находящейся на расстоянии l
= 75 см от источника колебаний, через t
= 0,01 с после начала колебаний. Скорость
распространения колебаний υ
= 300 м/с.
Решение
Запишем
уравнение волны, распространяющейся
от данного источника: x
= 0,04 sin
600 (t
–
).
Находим
фазу волны в данный момент времени в
данном месте:
t
–
= 0,01 –
= 0,0075 ,
600
∙
0,0075
= 4,5
,
sin
4,5
= sin
= 1.
Следовательно,
смещение точки x
= 0,04 м, т.е. на расстоянии l
=75
см от источника в момент времени t
= 0,01 c
смещение точки максимально.
Список литературы
-
Волькенштейн
В.С. Сборник задач по общему курсу
физики. – СПб.: СпецЛит, 2001. -
Савельев
И.В. Сборник вопросов и задач по общей
физике. – М.: Наука, 1998.
35
Соседние файлы в папке FIZIKA
- #
- #
- #
- #
- #
- #
- #
1. Упругие волны
1.1. Упругие продольные и поперечные волны
1.2. Характеристики бегущих волн
1.2.1. Длина волны
1.2.2. Фазовая скорость волны
1.2.3. Фазовая скорость различна для разных сред
1.2.4. Фронт волны. Волновая поверхность
1.2.5. Уравнение бегущей волны
1.2.6. Волновое уравнение
1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды
1.3. Энергия упругих волн
1.4. Принцип суперпозиции волн. Групповая скорость
1.5. Интерференция волн. Стоячие волны
2. Звуковые волны
3. Электромагнитные волны
Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие – волна. Волновые процессы представляют общий класс явлений, несмотря на их разную природу.
Процесс распространения колебаний в пространстве называется волной.
Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они “бегут” от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.
1. Упругие волны
1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.
Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.
Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.
2. Среда называется однородной, если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.
Среда называется изотропной, если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.
Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.
1.1. Упругие продольные и поперечные волны
Все волны делятся на продольные и поперечные.
Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.
Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.
Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига. Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды, или в твердых телах, где возникают деформации удлинения или сжатия. Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.
1.2. Характеристики бегущих волн
1.2.1. Длина волны
Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.
Длиной волны называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна
).
Если точки разделены расстоянием , их колебания происходят в противофазе.
1.2.2. Фазовая скорость волны
Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.
Фазовая скорость — это скорость распространения данной фазы колебаний, т.е. скорость волны.
Связь длины волны , фазовой скорости
и периода колебаний Т задается соотношением:
.
Учитывая, что , где
— линейная частота волны,
— период, а циклическая частота волны
, получим разные формулы для фазовой скорости:
.
Для волнового процесса характерна периодичность по времени и по пространству.
Т – период колебаний точек среды. Роль пространственного периода играет длина волны . Соотношение между периодом и циклической частотой задается формулой:
. Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом:
.
Таким образом. Можно добавить еще одно уравнение для фазовой скорости:
.
1.2.3. Фазовая скорость различна для разных сред
В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:
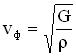
где — модуль сдвига среды,
-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
Фазовая скорость упругих продольных волн в твердом теле равна
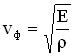
где Е — модуль Юнга, — плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
Фазовая скорость продольных волн в жидкости и газе определяется соотношением: 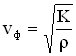
где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, — плотность невозмущенной среды.
Фазовая скорость продольных волн в идеальном газе задается формулой: 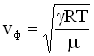
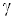
— молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (
) и от его термодинамического состояния (Т).
1.2.4. Фронт волны. Волновая поверхность
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.
Если известно положение фронта волны в некоторый момент времени и скорость волны , то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.
1.2.5. Уравнение бегущей волны
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.
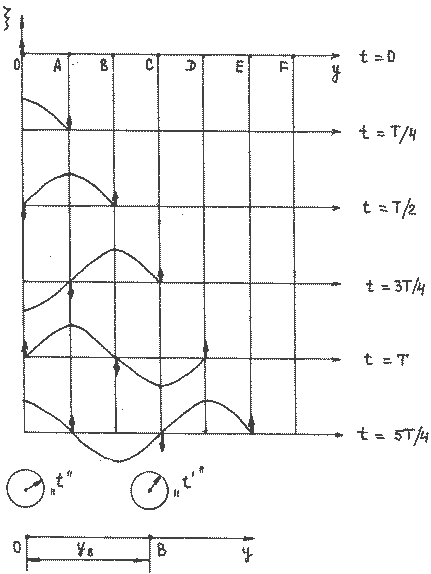
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О — центр (источник) колебаний, она колеблется по закону:
,
где — смещение точки О от положения равновесия,
— частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.
Через промежуток времени процесс колебаний дойдет до точки В, и она будет колебаться по закону:
.
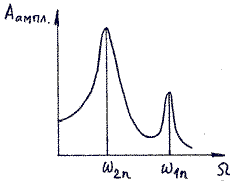
Рисунок 2.1.1.
Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время . Моменты времени t и
связаны между собой соотношением
или
. Расстояние между точками О и В обозначим
. Фазовая скорость волны равна
, тогда
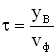
и
и формулы
и
, можно записать уравнение колебаний точки В в разных видах:
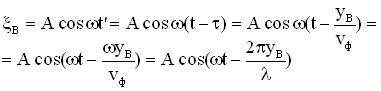
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:
,
где — волновое число (см. определение выше).
Это уравнение и есть уравнение для смещения любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина
— фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.
Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.
Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:
.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.
1.2.6. Волновое уравнение
Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:
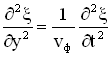
— фазовая скорость волны.
Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что есть функция двух переменных t и y.
1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:
,
то скорость этой точки есть величина , а ускорение —
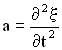
,
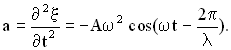
1.3. Энергия упругих волн
В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме равна:
, где
— объемная плотность среды.
Если выбранный объем записать как , где S – площадь его поперечного сечения, а
— его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком
через его поверхность:
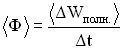
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.
Эта величина определяется соотношением:
,
где 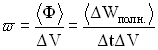
— фазовая скорость волны. Так как фазовая скорость волны
— вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:
.
Величина , вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова — Пойнтинга.
Интенсивностью волны называется модуль среднего значения вектора Умова 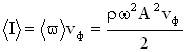
1.4. Принцип суперпозиции волн. Групповая скорость
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
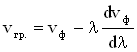
1.5. Интерференция волн. Стоячие волны
1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.
В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине , где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна
, т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.
Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.
2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источники и
испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника
, а от второго —
.
Колебания точки М под действием волн от двух источников и
описываются уравнениями:
,
. Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”):
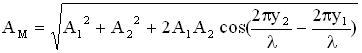
), если
, где
Величина
называется разностью хода двух волн. Условие максимума при интерференции имеет вид:
. Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (
), если
, (
). Условие минимума при интерференции имеет вид:
. Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид:
,
Суммарное смещение
частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений
и
:
.
Это и есть уравнение стоячей волны. Величина 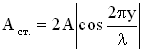
) — фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.
В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:
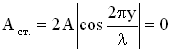
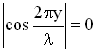
для
Итак, координаты узлов задаются формулой:
.
Расстояние между двумя соседними узлами равно .
Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:
.
Это уравнение можно получить из условия максимума амплитуды
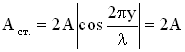
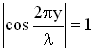
(
).
Расстояние между двумя соседними пучностями равно .
4. Изменение фазы волны при ее отражении.
Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на
радиан соответствует появлению дополнительного хода луча, равного
.
2. Звуковые волны
1. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.
Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.
2. Избыточное звуковое давление. Уравнение звуковой волны.
Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.
Если — давление и плотность невозмущенной среды (среды, по которой не проходит волна), а
— давление и плотность среды при распространении в ней волнового процесса, то величина
называется избыточным давлением. Величина
есть максимальное значение избыточное давление (амплитуда избыточного давления).
Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:
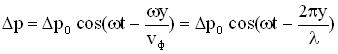
где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.
Если ввести величину избыточной плотности и ее амплитуды
так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так:
. 3. Объективные и субъективные характеристики звука.
Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.
К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.
Таблица 3.
| Субъективные Характеристики | Объективные характеристики |
| Высота звука | Высота звука определяется частотой волны |
| Тембр (окраска звука) | Тембр звука определяется его спектром |
| Громкость (сила звука) | Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды) |
Остановимся на некоторых определениях.
Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.
Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).
Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.
Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.
3. Электромагнитные волны
1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.
Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:
где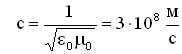
,
— электрическая и магнитная постоянные,
,
— соответственно диэлектрическая и магнитная проницаемость среды.
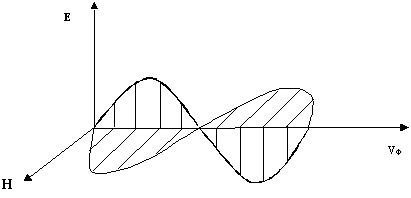
2. Электромагнитные волны — поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).
Для сравнения ориентации тройки векторов , Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.
Рисунок 2.1.4
Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:
которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
3. По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..
Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты . Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:
Такие волны называются плоско (или линейно) поляризованными волнами.
Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).
4. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.
Стоячая электромагнитная волна состоит из двух стоячих волн — магнитной и электрической, колебания которых сдвинуты по фазе на .
5. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением: 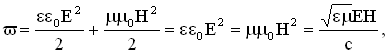
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:
соответственно объемная плотность энергии этой волны
Значение объемной плотности энергии волны меняется за период от 0 до .Среднее за период значение энергии равно:
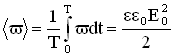
6. Вектор плотности потока энергии электромагнитной волны называется вектором Умова — Пойнтинга:
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен:
Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:
Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность бегущей монохроматической волны: — фазовая скорость волны,
среднее значение объемной плотности энергии поля волны.
Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.



![Rendered by QuickLaTeX.com [T=2pi sqrt{frac{l}{g}}]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-29425af3eec4256686ccf44fde46b3ca_l3.png)