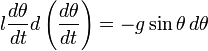Как найти период колебания физического маятника - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое колебательный процесс

Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.

Систему, совершающую колебания, называют колебательной системой или осциллятором.

Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.

Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.

При механических колебаниях, которые относят к категории вынужденных:

(F=F_{0}cos cot)

Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.

Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.

Определение периода колебаний, формула

Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:

(x(t)=Atimes cos left(omega _{0}t+phi _{0} right))

Где (x(t)) является отклонением колеблющейся физической величины от равновесного значения;

А представляет собой амплитуду гармонических колебаний;

(omega _{0}) равно циклической или круговой частоте колебаний;

(phi _{0}) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;

(cp(t)=(co_{0}t+cp_{0})) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.

В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:

(cos left(alpha +2pi right)=cos alpha,)

то х остается без изменений при фазе колебаний, получающей приращение в $$2pi$$

Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.

В этом случае фаза будет увеличена на (2pi:)

(omega _{0}(t+T)+phi _{0}=left(omega _{0}t+phi _{0} right)+2pi)

Из данного равенства можно вычислить период колебаний:

(T=frac{2pi }{omega _{0}})

Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:

(v=frac{omega _{0}}{2pi})

На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.

Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.

Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:

Смещение (x=Atimes cos left(omega _{0}t+phi _{0} right))

Скорость (v_{x}=dot{x}=-Aomega _{0}times sin left(omega _{0} t+phi_{0} right)=Aomega _{0}times cos left(omega _{0} t+phi_{0} +frac{pi }{2}right))

Ускорение

(a_{x}=dot{v_{x}}=ddot{x}=-Aomega _{0}times cos left(omega _{0} t+phi_{0} right)=Aomega _{0}^{2}times cos left(omega _{0} t+phi_{0} +pi right))

Как найти период для физического маятника

В случае, когда углы отклонения (varphi) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:

(F=mgtimes sin varphi)

Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла (alpha)

Учитывая малый угол (varphi) уравнение можно записать в следующем виде:

(F=mgtimesvarphi)

С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:

(J=ml^{2})

При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:

(frac{d^{2}varphi }{dt^{2}}+frac{mgl}{J}varphi =0)

В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:

(alpha _{x}(t)+omega ^{2}x(t)=0)

Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:

(omega =sqrt{frac{mgl}{J}})

В таком случае для расчета периода колебаний математического маятника будет использоваться формула:

(T =frac{2pi }{omega }=2pi sqrt{frac{J}{mgl}})

Исходя из расчетов, можно сделать следующие выводы:

Период пружинного маятника (T =2pi sqrt{frac{m}{k}})
Период математического маятника (T =2pi sqrt{frac{L}{g}})
Период крутильного маятника (T =2pi sqrt{frac{I}{K}})

В приведенных формулах:

T — период физического маятника;
J — момент силы маятника относительно оси вращения;
l — расстояние от оси вращения до центра масс;
m — масса маятника;
g=9.8 — ускорение свободного падения.

Примеры решений

Задача № 1

Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.

Решение

(T =frac{t}{N}=frac{120}{60}=2)

(V=frac{1}{T}=frac{1}{2}=0.5)

Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.

Задача № 2

Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.

Решение

А = 20

Т = 0,8

(V=frac{1}{T}=frac{1}{0,8}=1,25)

(x(t)=Asin 2pi Vt=0.2sin 2pi times 1.25t=0.2sin 2.5pi t)

Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: (x(t)=0.2sin 2.5pi t)

Задача № 3

Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.

Решение

Период колебаний математического маятника рассчитывается по формуле:

(T =2pi sqrt{frac{L}{g}})

Согласно определению:

(V=frac{1}{T})

Тогда:

(T=frac{1}{V})

Получим равенство:

(frac{1}{V}=2pi sqrt{frac{l}{g}})

Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:

(frac{1}{V^{2}}=4pi ^{2}times frac{l}{g}Rightarrow l=frac{g}{4pi ^{2}V^{2}})

(l=frac{1.5}{4*3.14 ^{2}*0.5^{2}}approx 0.16)

Ответ: длина математического маятника примерно составляет 0,16 метра.

Источник

Период физического маятника — твердое тело, совершающее колебания в гравитационном поле вокруг горизонтальной оси подвеса, расположенной выше его центра тяжести.

$Large T=2pi sqrt{frac{J}{mgl}}$

Давай те выведем формулу для периода физического маятника.

При небольших углах отклонения физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла . Так как угол маленький, у нас получается, что F равно:

Для вывода закона движения физического маятников используем основное уравнение динамики вращательного движения:

Так как момент силы определить в явном виде нельзя. Надо записать дифференциальное уравнение колебаний физического маятника:

$large frac{d^2varphi }{dt^2}+frac{mgl}{J}varphi =0$

Сравнивая полученное выражение с уравнением гармонических колебаний:

Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

$large omega=sqrt{frac{mgl}{J}}$

Тогда период колебаний математического маятника будет равен:

$Large T=frac{2pi }{omega } =2pi sqrt{frac{J}{mgl}}$

Так же есть:

Период пружинного маятника $T=2pi sqrt{frac{m}{k}}$

Период математического маятника $T=2pi sqrt{frac{L}{g}}$

Период крутильного маятника $T=2pi sqrt{frac{I}{K}}$

В Формуле мы использовали :

— Период физического маятника

— Момент силы маятника относительно оси вращения

— Расстояние от оси вращения до центра масс

— Масса маятника

— Ускорение свободного падения

Источник

Период колебаний физического маятника

Для
того, чтобы найти период колебаний
физического маятника, необходимо решить
уравнение качания.

Для этого умножим
левую
и
правую часть этого уравнения на
.
Тогда:

Интегрируя
это уравнение, получаем.

где
произвольная
постоянная. Её можно найти из граничного
условия, что в моменты
.
Получаем:
.
Подставляем и преобразовываем получившееся
уравнение:

Отделяем
переменные и интегрируем это уравнение:

Удобно
сделать замену переменной, полагая
.
Тогда искомое уравнение принимает вид:

Здесь
— нормальный
эллиптический интеграл Лежандра 1-го
рода.
Для периода колебаний получаем формулу:

Здесь
— полный
нормальный эллиптический интеграл
Лежандра 1-го рода.
Раскладывая его в ряд, можно получить
удобную для практических вычислений
формулу:

[Править]Период малых колебаний физического маятника

Если
амплитуда колебаний
мала,
то корень в знаменателе эллиптического
интеграла приближенно равен единице.
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:

Эта
формула даёт результаты приемлемой
точности (ошибка менее 1 %) при углах,
не превышающих 4°.

Следующий
порядок приближения можно использовать
с приемлемой точностью (ошибка менее
1 %) при углах до 1 радиана (≈60°)

Вопрос 4. Энергия гармонических колебаний

При механических колебаниях
колеблющееся тело (или материальная
точка) обладает кинетической и
потенциальной энергией. Кинетическая энергия
тела W:

(Скорость
тела v = ds/dt)

Для
вычисления потенциальной энергии тела
воспользуемся самой общей формулой,
связывающей силу и потенциальную энергию
тела в поле этой силы:

где
U — потенциальная энергия, набираемая
(или теряемая) телом, движущимся в силовом
поле F от точки 0 (точки, в которой
потенциальная энергия принимается
равной 0) до точки х.

Для
силы, линейно зависящей от смещения
(как в случае наших механических
маятников, такие силы носят общее
название квазиупругих сил) мы имеем:

Сравнивая
формулы

для кинетической и
потенциальной энергии механического
маятника, можно сделать следующие
выводы:

1.
Полная механическая энергия тела не
изменяется при колебаниях:

2.
Частота колебаний кинетической и
потенциальной энергии в 2 раза больше
частоты колебаний маятника.

3.
Колебания кинетической и потенциальной
энергии сдвинуты друг относительно
друга по фазе на  (на
полпериода). Когда кинетическая энергия
достигает максимума, потенциальная —
минимума (нуля) и наоборот. Энергия при
колебаниях постоянно перекачивается
из потенциальной в кинетическую и
обратно.

Вопрос 5.

Ускоре́ние
свобо́дного паде́ния g (оно
же ускорение силы тяжести), — ускорение,
придаваемое телу в вакууме силой
тяжести,
то есть геометрической
суммой гравитационногопритяжения
планеты (или другого астрономического
тела) и сил
инерции,
вызванных её вращением, за
исключением кориолисовых
сил инерции^[1].
В соответствии со вторым
законом Ньютона,
ускорение свободного падения численно
равно силе тяжести, воздействующей на
объект единичной массы.

Значение
ускорения свободного падения на
поверхности Земли обычно
принимают равным 9,8 или 10 м/с².
Стандартное («нормальное») значение,
принятое при построении систем единиц, g =
9,80665 м/с²^[2],
а в технических расчётах обычно
принимают g =
9,81 м/с².

Стандартное
значение g было
определено как «среднее» в каком-то
смысле ускорение
свободного падения на
Земле, примерно равно ускорению свободного
падения на широте45,5°
на уровне
моря.

Реальное
ускорение свободного падения на
поверхности Земли зависит от широты,
времени суток и других факторов. Оно
варьируется от 9,780 м/с² на экваторе до
9,832 м/с² наполюсах^[3].
Оно может быть вычислено (в м/с²) по
эмпирической формуле:

где
—
широта рассматриваемого места,
— высота
над уровнем моря в метрах.^[4] Эта
формула применима лишь в ограниченном
диапазоне высот от 0 до нескольких
десятков км, где убывание ускорения
свободного падения с высотой можно
считать линейным (на самом же деле оно
убывает квадратично).

Как
в лабораторке измеряли я хз ибо проебал^^

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Физический маятник — твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.

Определения

Момент инерции относительно оси, проходящей через точку подвеса:

${displaystyle I=mleft(r^{2}+h^{2}right)}$

Дифференциальное уравнение движения физического маятника

Пренебрегая сопротивлением среды, дифференциальное уравнение качания физического маятника записывается следующим образом:

${displaystyle I{frac {d^{2}theta }{dt^{2}}}=-mghsin theta }$

Полагая ${displaystyle {frac {r^{2}}{h}}+h=l}$ , предыдущее уравнение можно переписать в виде:

${displaystyle l{frac {d^{2}theta }{dt^{2}}}=-gsin theta }$

Величина называется приведенной длиной.

Центр качания физического маятника

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящий от точки подвеса через центр тяжести точку на расстоянии от точки подвеса. Эта точка и будет центром качания маятника.

Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен ${displaystyle I=ml^{2},}$ , а момент силы тяжести относительно той же оси . Легко заметить, что уравнение движения не изменится.

Теорема Гюйгенса

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Доказательство

Вычислим приведенную длину для нового маятника:

${displaystyle l_{1}={frac {r^{2}}{r^{2}/h}}+{frac {r^{2}}{h}}=h+{frac {r^{2}}{h}}=l}$

Период колебаний физического маятника

Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на ${displaystyle {frac {d^{2}theta }{dt^{2}}}dt=dleft({frac {dtheta }{dt}}right)}$ , а правую часть на . Тогда:

${displaystyle l{frac {dtheta }{dt}}dleft({frac {dtheta }{dt}}right)=-gsin theta ,dtheta }$

Интегрируя это уравнение, получаем.

${displaystyle lleft({frac {dtheta }{dt}}right)^{2}=2gcos theta +C}$

где произвольная постоянная. Её можно найти из граничного условия, что в моменты ${displaystyle theta =pm alpha ,,,,{frac {dtheta }{dt}}=0}$ . Получаем: . Подставляем и преобразовываем получившееся уравнение:

${displaystyle {frac {dtheta }{dt}}=2{sqrt {frac {g}{l}}}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}}$

Отделяем переменные и интегрируем это уравнеие:

${displaystyle {sqrt {frac {g}{l}}}t=int limits _{0}^{theta }{frac {dleft({frac {theta }{2}}right)}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}}}$

Удобно сделать замену переменной, полагая ${displaystyle sin {frac {theta }{2}}=sin {frac {alpha }{2}}sin varphi }$ . Тогда искомое уравнение принимает вид:

${displaystyle t={sqrt {frac {l}{g}}}int limits _{0}^{varphi }{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}={sqrt {frac {l}{g}}}Fleft(varphi setminus alpha /2right)}$

Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:

${displaystyle T=4{sqrt {frac {l}{g}}},int limits _{0}^{pi /2}{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}=4{sqrt {frac {l}{g}}},Kleft(sin {frac {alpha }{2}}right)}$

Здесь ${displaystyle Kleft(sin {frac {alpha }{2}}right)}$ — полный нормальный эллиптический интеграл Лежандра 1-го рода.

Период малых колебаний физического маятника

Если амп мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

${displaystyle T=2pi {sqrt {frac {l}{g}}}=2pi {sqrt {frac {I}{mgh}}}}$

Отсюда видно, что физический маятник колеблется так же, как математический маятник с приведенной длиной.

См. также

Математический маятник

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Физический маятник. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник

Период и частота колебаний, теория и онлайн калькуляторы

Период и частота колебаний

Период колебаний

Определение

Период — это отрезок времени, которое необходимо для совершения одного цикла периодического процесса.

Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.

За время равное периоду колебаний фаза изменяется на величину равную $2pi $, поэтому:

[T=frac{2pi }{{omega }_0}left(1right).]

Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.

Гармонические колебания некоторого параметра $xi $ описываются уравнением:

[xi =A{cos ({omega }_0t+varphi ) } left(2right),]

где $A={xi }_{max}$ — амплитуда колебаний; ${omega }_0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ —
фаза колебаний. Величина $xi $ лежит в пределах $-Ale sle $+A.

Формулы для вычисления периода простейших колебательных систем

Период колебаний пружинного маятника определим как:

[T=2pi sqrt{frac{m}{k}} left(3right),]

на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.

Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)

[T=2pi sqrt{frac{l}{g}}left(4right).]

Формула для вычисления периода колебаний физического маятника представляет собой выражение:

[T=2pi sqrt{frac{J}{mga}left(5right),}]

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние от центра масс тела до оси вращения.

Единицами измерения периода служат единицы времени, например секунды.

[left[Tright]=c.]

Частота колебаний

Определение

Физическая величина обратная периоду колебаний называется частотой колебаний ($nu $).

Частота — это количество полных колебаний, которые колебательная система совершает за единицу времени.

[nu =frac{1}{T}left(6right).]

Частота колебаний связана с циклической частотой как:

[{omega }_0=2pi nu left(7right).]

Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:

[left[nu right]=с^{-1}=Гц.]

Примеры задач с решением

Пример 1

Задание. Каковы период ($T$) и частота ($nu $) колебаний, которые происходят в соответствии с уравнением: $x=A{sin ({omega }_0(t+tau )) }$, где ${omega }_0=2,5 pi (frac{рад}{с})$; $tau =0,4 $с?

Решение. Из уравнения колебаний:

[x=A{sin left({omega }_0left(t+tau right)right)left(1.1right), }]

заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:

[T=frac{2pi }{{omega }_0}left(1.1right).]

Подставляя имеющиеся данные, вычислим период колебаний:

[T=frac{2pi }{2,5pi }=0,8 left(сright).]

Частоту колебаний найдем как величину, обратную периоду:

[nu =frac{1}{T}left(1.2right).]

Вычислим частоту:

[nu =frac{1}{0,8}=1,25 left(Гцright).]

Ответ. $T=0,8$ с; $nu =1,25 Гц$

Пример 2

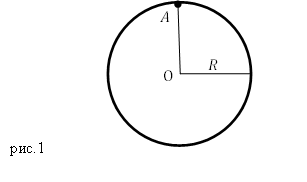
Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.

Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:

[T=2pi sqrt{frac{J}{mga}left(2.1right).}]

Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:

[a=R left(2.2right).]

Найдем момент инерции обруча относительно оси, перпендикулярной плоскости обруча, проходящей через точку $A$. Для этого воспользуемся теоремой Штейнера:

[J=J_0+mR^2 left(2.3right),]

где $J_0=mR^2$ — момент инерции обруча, относительно оси, проходящей через его центр (т.О), перпендикулярно плоскости обруча; расстояние между осями равно радиусу обруча. Получаем, момент инерции обруча относительно гвоздя равен:

[J=mR^2+mR^2=2mR^2left(2.4right).]

Используя формулы (2.1) (2.2) и (2.4), имеем:

[T=2pi sqrt{frac{2mR^2}{mgR}}=2pi sqrt{frac{2R}{g}}.]

Отталкиваясь от полученного результата, найдем частоту колебаний как:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{g}{2R}}.]

Ответ. $T=2pi sqrt{frac{2R}{g}},$ $nu =frac{1}{2pi }sqrt{frac{g}{2R}}$

Читать дальше: полная энергия колебаний.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник