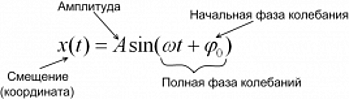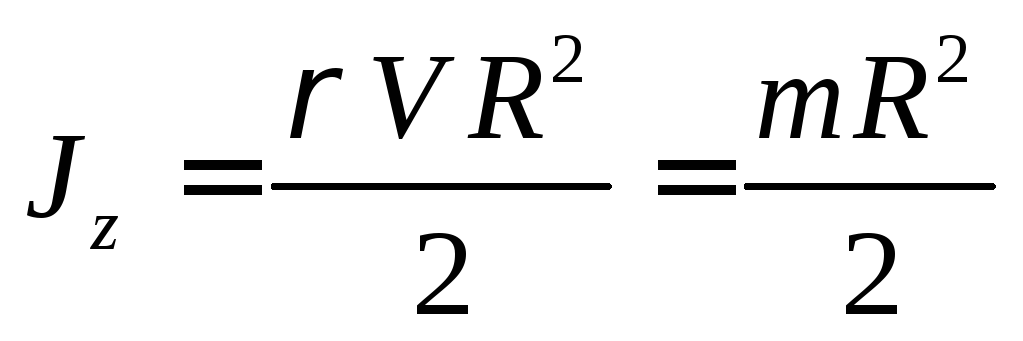Как найти период максимальной кинетической энергии

Кинетическая энергия

Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.

В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия. По мере движения вниз под действием силы тяжести, скорость груза нарастает и достигает максимума в нижней точке, после чего снова начинает запасаться по мере движения вверх.

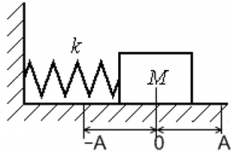
Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают — потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром — коэффициентом упругости.

Максимальная кинетическая энергия груза

Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как

$E = E_p + E_k = frac{m cdot v^2}{2} + frac{k cdot x^2}{2}$, где:

• $E_p$ — потенциальная энергия,
• $E_k$ — кинетическая энергия,
• $m$ — масса,
• $v$ — моментальная скорость,
• $k$ — коэффициент упругости,
• $x$ — приращение длины пружины в данный момент.

«Максимальная кинетическая энергия груза: формула» 👇

Максимальную кинетическую энергию можно вычислить как

$(E_k)_{max} = frac{m cdot v_{max}^2}{2}$,

где $v_{max}$ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:

$(E_k)_{max} = (E_p)_{max} = frac{k cdot x_{max}^2}{2}$,

где $x_{max}$ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.

Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.

Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.

Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac{1}{T}$ , где

v ― частота [Гц];

T ― период [c].

Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac{N}{t}$ , где

ν ― частота [Гц];

N ― количество колебаний;

t - время [с].

Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac{2pi}{T}$ , где

ω ― циклическая частота [рад/с];

ν ― частота [Гц];

T ― период [c].

Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:

x(t) = Asin(ωt + φ0) или x(t) = Acos(ωt + φ0), где

x ― смещение [м];

t ― время, [с];

A ― амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

φ0 ― начальная фаза колебаний, [рад];

(ωt + φ0) ― полная фаза колебаний [рад].

Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.

Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.

Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.

Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где

φ ― полная фаза колебаний [рад];

φ0 ― начальная фаза колебаний, [рад];

ω ― циклическая частота [рад/с];

t ― время, [с].

Пример анализа гармонических колебаний точки

Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где

x ― смещение [м];

t ― время, [с];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с].

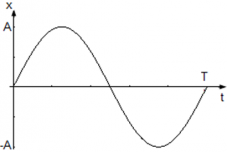
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac{pi}{2} +2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac{3pi}{2} +2pi n$ , где n = 0, 1 , 2, … N.

График колебания координаты точки имеет вид:

Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где

v ― скорость движения точки [м/с];

x ― координата точки [м];

t ― время, [с].

Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).

Уравнение скорости точки равно v(t) = Acos(ωt), где

v ― скорость движения точки [м/с];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

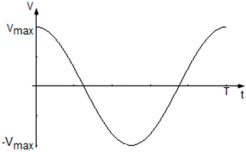
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.

График колебания скорости точки имеет вид:

Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.

Ускорение ― это производная скорости по времени: a = vt‘, где

a ― ускорение движения точки [м/с2];

v ― скорость движения точки [м/с];

t ― время, [с].

Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).

Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где

a ― ускорение движения точки [м/с2];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

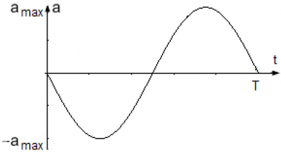
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.

График колебания ускорения точки имеет вид:

Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где

E ― полная механическая энергия системы, E = const, [Дж];

EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];

EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].

Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).

Потенциальная энергия деформированной пружины равна EП = $frac{kx^2}{2}$ , где

EП ― потенциальная энергия деформированной пружины, [Дж];

k ― коэффициент упругости пружины [Н/м];

x ― деформация пружины (величина ее удлинения или сжатия) [м].

У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac{k(x(t))^2}{2}$ = $frac{k(Asin(omega t))^2}{2}$ = $frac{k}{2} cdot A^2 sin^2 (omega t)$ .

Уравнение потенциальной энергии пружинного маятника EП = $frac{k}{2} cdot A^2 sin^2 (omega t)$ , где

EП ― потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac{k}{2}A^2$ , где

EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

A — амплитуда колебаний [м].

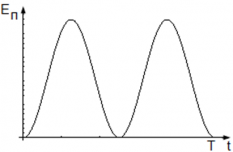
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.

График колебаний потенциальной энергии пружинного маятника:

Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac{mv^2}{2}$ , где

Eк ― кинетическая энергия тела, [Дж];

m ― масса тела, [кг];

v ― скорость движения тела, [м/с].

У тела, которое совершает колебательные движения, скорость ― переменная величина.

Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac{m(v(t))^2}{2}$ = $frac{m}{2} cdot (Aomegacos(omega t))^2$ = $frac{m}{2} cdot A^2 omega^2 cos^2 (omega t)$ .

Уравнение кинетической энергии маятника Eк = $frac{m}{2} cdot A^2 omega^2 cos^2 (omega t)$ , где

Eк ― кинетическая энергия маятника, [Дж];

m ― масса тела, [кг];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с];

t ― время, [с].

Амплитуда кинетической энергии маятника равна EКmax = $frac{m}{2} cdot A^2 omega^2$ , где

EКmax ― максимальная кинетическая энергия маятника, [Дж];

m ― масса тела, [кг];

A — амплитуда колебаний [м];

ω ― циклическая частота [рад/с].

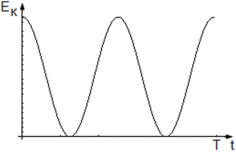
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.

График колебаний кинетической энергии маятника:

Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.

Период колебаний математического маятника равен T = $2pi sqrt{frac{l}{g}}$ , где

T ― период колебаний [с];

l ― длина нити математического маятника [м];

g ― ускорение свободного падения [м/с2].

Период колебаний пружинного маятника равен T = $2pi sqrt{frac{m}{k}}$ , где

T ― период колебаний [с];

m ― масса груза [кг];

k ― жесткость пружины [Н/м].

Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.

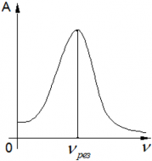
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.

На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.

Формулы пружинного маятника в физике

Формулы пружинного маятника

Определение и формулы пружинного маятника

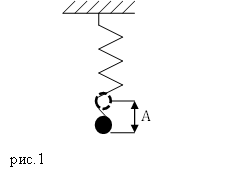
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

[ddot{x}+{omega }^2_0x=0left(1right),]

где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]

где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

[T=2pi sqrt{frac{m}{k}}left(4right).]

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]

начальная фаза при этом:

[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

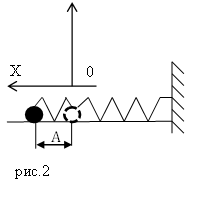
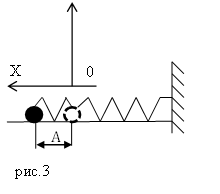
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

[E_p=-frac{dF}{dx}(8)]

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]

Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]

где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Читать дальше: формулы равноускоренного прямолинейного движения.

Введём энергию колебания.

Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:

(1)

• где

Вспомним зависимость скорости от времени при гармоническом колебании:

(2)

• где

Подставим (2) в (1) при условии (для упрощения):

=  (3)

Тогда максимальная кинетическая энергия данной системы:

(4)

т.к. максимальное значение .

С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:

(5)

• где

Вспомним зависимость координаты от времени при гармоническом колебании:

(6)

Подставим (5) в (4) при условии (для упрощения):

=  (7)

Тогда максимальная потенциальная энергия данной системы:

(8)

т.к. максимальное значение .

Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).

Энергия и работа при вращательном движении

Формула вычисления работы для поступательного прямолинейного движения имеет вид: W = F·s (Н·м) или (Дж).

Для того, чтобы вывести аналогичную формулу для вращательного движения, необходимо силу F преобразовать в момент силы M, а перемещение s, в угол Θ

Пусть для вращения колеса, радиусом r, прикладывается сила F, как показано на рисунке ниже.

Чему будет равна работа этой силы?

Для вычисления работы применим формулу:

При вращательном движении перемещение s будет равно произведению радиуса колеса r на его угол поворота Θ:

Момент М, создаваемой силой F, вычисляется по формуле:

Таким образом, работа будет равна:

Мы получили формулу вычисления работы для вращательного движения (угол поворота должен быть указан в радианах) — это произведение момента силы на угол поворота.

Вычислим работу, которую совершит колесо автомобиля после 10 оборотов, при условии, что к нему был приложен постоянный момент силы в 100 Н·м:

Кинетическая энергия вращательного движения

Кинетическая энергия объекта, массой m, движущегося поступательно со скоростью v, вычисляется по формуле: K = 1 /₂·(m·V 2 ).

Для получения формулы вычисления кинетической энергии для вращательного движения необходимо заменить массу тела m на момент инерции I, а скорость v на угловую скорость ω.

Формула связи тангенциальной скорости v и угловой скорости ω выглядит следующим образом (подробнее смотри «Параметры вращательного движения»):

Подставим это соотношение в предыдущую формулу:

Следует сказать, что данная формула расчета кинетической энергии подходит только для материальной точки.

Формула для вычисления кинетической энергии протяженного объекта будет выглядеть следующим образом:

В случае, если все материальные точки протяженного объекта вращаются с одинаковой угловой скоростью, ее можно вынести за знак суммирования:

Вспомним формулу момента инерции, и сделаем подстановку:

Закрепим полученные теоретические знания на практике, решив интересную задачу.

Предположим, что по наклонной плоскости скатываются два цилиндра одинаковой массы — полый и цельный. Выясним, какой из этих цилиндров скатится быстрее, т.е. будет иметь бОльшую скорость в конце наклонной плоскости.

Решая задачи подобного типа, надо понимать, что, если бы цилиндры просто скользили вниз по наклонной плоскости без вращения, то их потенциальная энергия превращалась бы в кинетическую энергию поступательного движения:

В нашем случае, потенциальная энергия цилиндров превращается в кинетическую энергию, как поступательного, так и вращательного движения:

Поскольку угловая скорость вычисляется по формуле ω=v/r, получим следующее равенство, и выведем формулу для вычисления скорости движения цилиндров:

Для обоих цилиндров все параметры в формуле одинаковы, за исключением момента инерции I (подробнее смотри «Момент инерции протяженного объекта»):

• для полого цилиндра: I=mr 2 ;
• для цельного цилиндра: I= 1 /₂mr 2

Подставляем соответствующие значения для момента инерции в формулу вычисления скорости цилиндров, и проводим несложные алгебраические преобразования:

Соотношение скоростей цилиндров будет равно:

Таким образом, скорость полого цилиндра будет немного ниже, чем цельного, следовательно, цельный цилиндр быстрее скатится по наклонной плоскости.

С физической точки зрения данный факт объясняется достаточно просто. В полом цилиндре основная масса материальных точек сосредоточена на краю цилиндра (на расстоянии радиуса от его центра), в то время, как в цельном цилиндре материальные точки распределены равномерно по всему радиусу, т.е., при одинаковой угловой скорости в полом цилиндре количество материальных точек, обладающих высокой тангенциальной скоростью, будет больше, чем в цельном, поэтому, полому цилиндру понадобится потратить больше энергии на свой разгон.

Если вам понравился сайт, будем благодарны за его популяризацию Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Закон сохранения энергии для вращательного движения

1. Момент импульса, законы изменения и сохранения момента импульса.

2. Работа и кинетическая энергия при вращательном движении. Закон изменения и сохранения механической энергии при вращательном движении.

3. Сопоставление поступательного и вращательного движений. Заключение.

ОТВОДИМОЕ ВРЕМЯ: 2 часа.

1. Суханов курс физики. – М.: 1996.

2. Савельев общей физики. Том 1. – M: – Наука, 1996. § 29, 41,42,43.

3. Трофимова физики. – М.: Высшая школа, 1999. § 17,19.

4. , Детлаф по физике. – М.: Наука, 1996. Глава 5.

Материальное обеспечение занятия:

Демонстрации: «Скамья Жуковского», «Фигурист».

Наряду с законами сохранения энергии и импульса закон сохранения момента импульса является одним из важнейших Фундаментальных законов природы.

В физике понятие, момента импульса расширяют на немеханические системы (которые не подчиняются законам Ньютона) и постулируют закон сохранения импульса для всех физических процессов.

I. МОМЕНТ ИМПУЛЬСА. ЗАКОН ИЗМЕНЕНИЯ И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Вспомним основной закон динамики вращательного движения:

(1)

учтем, что и подставим в (1)

,

Поскольку предполагалось, что момент инерции J=const можно внести его под знак дифференциала.

Тогда получим . Векторную величину называют моментом импульса твердого тела относительно оси. Тогда можно записать так:

(2)

Скорость изменения момента импульса тела равна векторной сумме моментов сил, действующих на тело.

Это более общая формулировка основного закона вращательного движения, она справедлива и для тела с изменяющимся моментом инерции.

Момент импульса измеряется в 1кг·м/с. Килограмм-метр в квадрате в секунду равен моменту импульса тела с моментом инерции 1кг·м, вращающегося с угловой скоростью 1рад/с.

Момент импульса – вектор, его направление всегда совпадает с направлением угловой скорости (рис 1).

Выберем произвольную систему тел.

Ведем понятие момента импульса данной системы как векторную сумму моментов импульсов ее отдельных частей:

(3)

где все векторы определены относительно одной и той же оси враще­ния заданной системы отсчета. Момент импульса системы тел – величина аддитивная; момент импульса системы тел равен векторной сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.

Выясним, какая величина определяет изменение момента импульса системы тел. Продифференцируем (3) по-времени:

(4)

Из Формулы (2) ясно, что равна моменту всех сил, действующих на i-ю часть системы тел. Представим момент в виде векторной суммы моментов внутренних и внешних сил:

(5)

где – суммарный момент всех внутренних сил относительно данной оси, – суммарный момент всех внешних сил относительно той же оси.

Суммарный момент всех внутренних сил относительно любой точки равен нулю, так как внутренние силы – это взаимодействия между частицами системы. По третьему закону Ньютона эти силы попарно равны по модулю, противоположны по направлению и лежат на одной прямой, то есть имеют одинаковые радиус-векторы. Поэтому моменты сил каждой пары взаимодействия равны по модулю и противоположны по направлению, Значит, суммарный момент всех внутренних сил равен нулю.

(6)

В результате уравнение (5) принимает вид:

(7)

где – суммарный момент всех внешних сил, называемый также главным моментом.

Производная момента импульса системы по времени равна суммарному моменту всех внешних сил относительна данной оси.

Пришли к важному выводу в уравнении (7): момент импульса системы тел может изменяться под действием только суммарного момента всех внешних сил.

В проекциях на оси неподвижной прямоугольной декартовой сис­теме координат с началом в точке 0 закон изменения момента импуль­са системы записывается в виде:

(8)

Здесь Lx, Ly, Lx и Mx, My, Mx – моменты импульса системы и главные моменты внешних сил относительно соответствующих осей координат.

Из основного закона динамики вращательного движения следует закон сохранения момента импульса.

Момент импульса замкнутой системы относительно любой неподвижной точки не изменяется с течением времени.

Для замкнутой системы ; ,

(9)

Закон сохранения момента импульса принадлежит к числу самых фундаментальных физических законов, он связан с изотропностью пространства. Изотропность пространства проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора направления осей координат инерциальной системы отсчета, т. е. не изменяются при повороте в пространстве замкнутой системы как целого на любой угол.

Особый интерес представляет случай, когда момент импульса сохраняется для незамкнутой системы. Если относительно некоторой оси выбранной системы отсчета главный момент внешних сил то момент импульса системы тел относительно этой оси сохраняется.

Обычно и Однако, если главный момент внешних сил относительно какой-либо оси, проходящей через точку 0, тождественно равен нулю, то момент импульса системы относительно этой оси не изменяется с течением времени. Например, если , то Такой случаи рассматривается в демонстрации со скамьей Жуковского (рис. 2).

Система тел: скамья, человек, гантели,

Эта система не замкнутая, но момент внешних сил относительно вертикальной оси Z равен нул^, следовательно

(10)

Подставляем

Найдем (11)

где J0 – момент инерции скамьи с человеком, m – масса одной гантели, r1 – расстояние гантели до оси в первом случае, r2 – расстояние гантели до оси во втором случае.

возрастает, если r2

Пусть твердое тело движется поступательно под действием консервативных и неконсервативных сил, т.е. общий случай. Тогда равнодействующая всех сил, действующих на тело 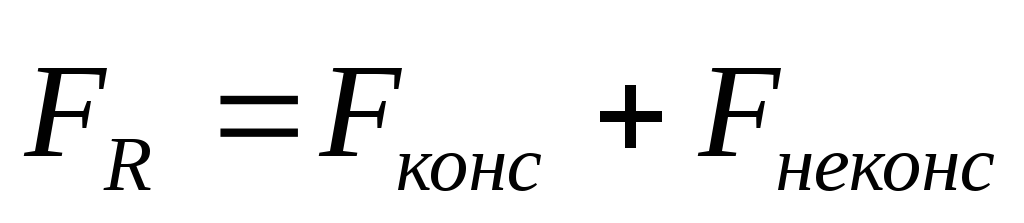. Работа равнодействующей всех сил в этом случае.

По теореме о кинетической энергии , а также учитывая, что, получим

– полная механическая энергия тела

(_*)

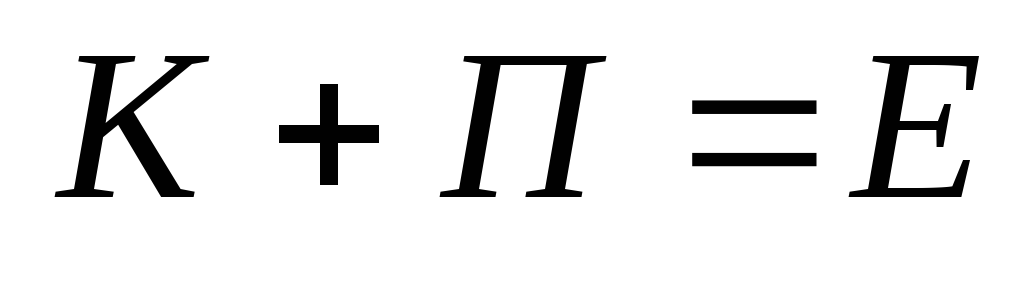
Если , то. Это и есть математическая запись закона сохранения энергии в механике для отдельного тела.

Формулировка закона сохранения энергии:

Полная механическая энергия тела не изменяется в отсутствии работы неконсервативных сил.

Для механической системы из Nчастиц нетрудно показать, что (_*) имеет место.

, при этом

Первая сумма здесь – суммарная кинетическая энергия системы частиц.

Вторая – суммарная потенциальная энергия частиц во внешнем поле консервативных сил

Третья – потенциальная энергия взаимодействия частиц системы друг с другом.

Вторая и третья суммы представляют собой полную потенциальную энергию системы.

, т.е.

Работа неконсервативных сил состоит из двух слагаемых, представляемых собой работу внутренних и внешних неконсервативных сил .

Также как и в случае движения отдельного тела, для механической системы из Nтел, если, то, и закон сохранения энергии в общем случае для механической системы гласит:

Полная механическая энергия системы частиц, находящихся только под действием консервативных сил, сохраняется.

Таким образом, при наличии неконсервативных сил полная механическая энергия не сохраняется.

Неконсервативными силами являются, например, сила трения , сила сопротивленияи другие силы, действия которых вызывают дессинацию энергии (переход механической энергии в теплоту).

Силы, приводящие к дессинации называются дессинативными. Некоторые силы не обязательно являются дессинативными.

Закон сохранения энергии имеет всеобщий характер и применим не только к механическим явлениям, но и ко всем процессам в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным. Энергия лишь может переходить из одной формы в другую.

Динамика вращательного движения

§12. Кинетическая энергия вращательного движения твердого тела. Момент инерции тел

Рассмотрим твердое тело, вращающееся на неподвижной оси.

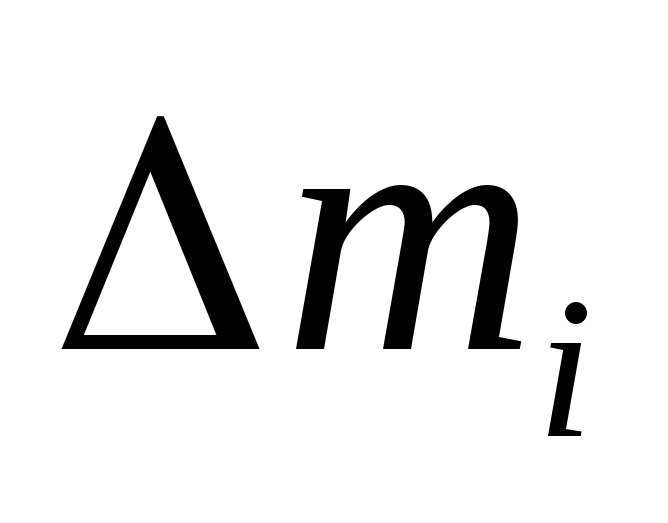
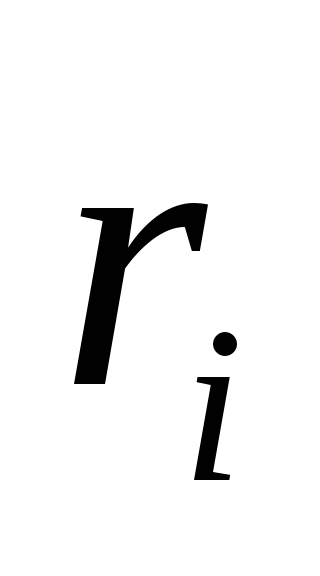
Мысленно разобьем его на Nэлементарных участков с массой, расстояние от которых до оси вращениямного больше линейных размеров участка. Тогда кинетическая энергия вращения тела вокруг осиzбудет равна сумме кинетических энергий всех элементарных участков,

(т.к. кинетическая энергия – величина аддитивная).

Ясно, что все элементарные участки вращаются по окружности, разного радиуса, но с одинаковой угловой скоростью ; для любого участка можно записать. С учетом этого равенства

Если размеры тела много меньше расстояния от него до некоторой его оси вращения z, то произведение массы этого тела на квадрат расстояния до данной оси вращения называется моментом инерции этого тела относительно оси вращенияz:

В нашем случае – моменты инерцииi-ых участков относительно осиz.

Моментом инерции всего тела вращения называется сумма моментов инерции всех его элементарных частей

Суммирование по элементарным участкам определяется разбиением, и лишь при , аесть предел и от разбиения не зависит. Поэтому точная формула для момента инерции есть:

Таким образом, кинетическая энергия есть

поступательное движение вращательное движение

– быстрота или скорость– скорость вращения

– мера инертностимера инертности

при движении при вращении

Моменты инерции некоторых однородных (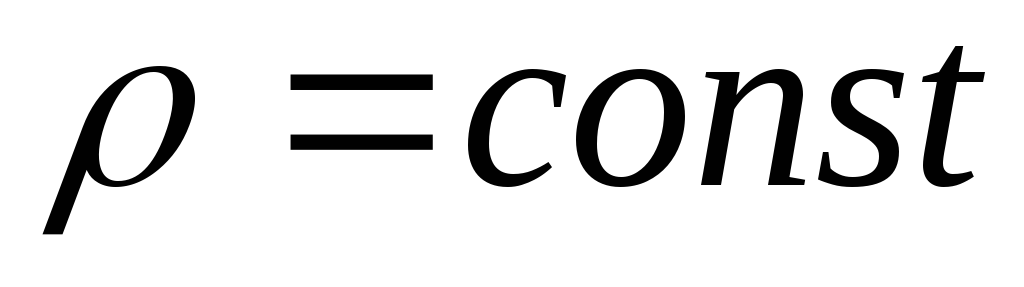) тел.

Момент инерции обруча или тонкостенного цилиндра относительно оси, проходящей через центр инертности перпендикулярно плоскости обруча.

Момент инерции диска или цилиндра относительно оси симметрии тела.

Выберем внутри цилиндра тонкостенный цилиндр с и толщиной.

Учитывая, что , получим

.

Момент инерции плоского стержня относительно оси, проходящей через центр тела и перпендикулярно к нему

Момент инерции шара относительно оси, проходящей через его центр.

1. Момент импульса вpащающегося, тела относительно оси

L = Jw.

2. Закон сохpанения момента импульса

SL = const.

где L – момент импульса i-го тела, входящего в состав системы. Закон сохpанения момента импульса для двух взаимодействующих тел

где J₁, J₂, w₁, w₂ – моменты инеpции и угловые скоpости

тел до взаимодействия, J₁ / , J₂ / , w₁ / , w₂ / – те же величины после

взаимодействия. Закон сохpанения момента импульса для одного тела, момент инеpции, котоpого меняется,

где J₁ и J₂ – начальный и конечный моменты инеpции, w₁ и w₂ –

начальная и конечная угловые скоpости тела.

3. Между формулами, описывающими поступательное и вращательное движения есть аналогия:

W_k = ( mv 2 )/2; W_k = (Jw 2 )/2;

С. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.

1. Уравнение гармонических колебаний

x = Acos(wt + j),

где х– смещение точки от положения равновесия;t – время;

А, w, j – соответственно амплитуда, угловая частота, начальная фаза колебаний; (wt + j)-фаза колебания в моментt

2. Угловая частота колебаний w = 2pn, или w = 2p/T,

где n и T – частота и период колебаний.

3. Скорость точки, совершающей гармонические колебания,

v = x / = – Awsin(wt + j).

4. Ускорение при гармоническом колебании

a = x // = – Aw 2 cos(wt + j).

5. Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящими по одной прямой, определяется по формуле

где А₁ и А₂ – амплитуды составляющих колебаний; j₁ и j₂ – их начальные фазы.

6. Дифференциальное уравнение гармонических колебаний материальной точки mx // = – kx, или x // + wx = 0,

гдеm – масса точки; k -коэффициент квазиупругой силы (kw 2 ) . 7. Полная энергия материальной точки, совершающей гармонические колебания, W = (mA 2 w 2 )/2 = (kA 2 )/2.

8. Период колебаний тела, подвешенного на пружине

T = 2pÖ(m/k),

где m – масса тела; k– жесткость пружины.

9. Период колебаний математического маятника T = 2pÖ(l/g),

гдеl – длина маятника; g – ускорение свободного падения.

10. Период колебаний физического маятника T = 2pÖ(J/mgl).

11. Период крутильных колебаний тела, подвешенного на упругой нити T = 2pÖ(J/k),

где J– момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.

12. Дифференциальное уравнение затухающих колебаний

mx // = – kx – rx / , или x // +2dx / + w 2 x = 0,

где r – коэффициент сопротивления; d – коэффициент затухания; d = r/(2m); w – cобственная частота колебаний (w = Ö(k/m).

13. Уравнение затухающих колебаний x = A . e – d t .cos(wt + j)

где А – начальная аплитуда; w – частота; е – основание натурального логарифма; d – коэффициент затухания.

14. Дифференциальное уравнение вынужденных колебаний

mx // = – kx – rx / + F .cos(wt), или x // + 2dx / + w 2 x = f .cos(wt).

где F .cos(wt) – внешняя периодическая сила, действующая на колеблющуюся точку и вызывающая вынужденные колебания; F – ее амплитудное значение; f = F /m.

Вариант 1.

Кинематика.

А.1. Пуля пущена с начальной скоростью vпод углом aк горизонту. Определить максимальную высоту подъема, дальность полета и радиус кривизны траектории пули в ее наивысшей точке.

Динамика.

Б.1.Через блок массой Мперекинута невесомая, нерастяжимая нить, к концам которой подвешены грузы с массами m₁и m₂ . Определить ускорения, с которыми будут двигаться грузы, если их предоставить самим себе, трением в оси блока пренебречь.

Законы сохранения при прямолинейном движении.

В.1.Тело массой m₁движется навстречу второму телу массой m₂ и абсолютно не упруго соударяется с ним. Скорости тел непосредственно перед ударом были v₁ и v₂ . Определить расстояние, пройденное телами после удара, если коэффициент трения μ ?

Энергия и работа.

Д.1. Под действием постоянной силы F вагонетка прошла путь Sи приобрела скорость v . Определить работу силы, если масса вагонетки равна m и коэффициент трения k .

Законы сохранения при вращательном движении.

Е.1. Стержень длиной Lи массой M может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня ударяет пуля массой m₂,летящая в горизонтальном направлении со скоростью vи застревает в нем. На какой угол отклонится стержень после удара?

6. Механические колебания.

С.1.Частица массой m совершает гармонические колебания с циклической частотой ω , по закону x= Asin(ωt). Определить период колебаний и амплитуду колебаний, если максимальная сила, действующая на частицу, равна F . Определить, также кинетическую, потенциальную и полную энергии через время tот начала колебания.

Вариант 2.

Кинематика.

А.2. Точка движется по окружности так, что зависимость пути от времени дается уравнением S = А – Bt + Ct 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорения.

Динамика.

Б.2.Акробат на мотоцикле описывает «мертвую петлю» радиусом R. С какой наименьшей скоростью должен проезжать акробат верхнюю точку петли, чтобы не сорваться?

Кинетическая энергия движения тела по окружности

«Физика — 10 класс»

Почему для увеличения угловой скорости вращения фигурист вытягивается вдоль оси вращения.
Должен ли вращаться вертолёт при вращении его винта?

Заданные вопросы наводят на мысль о том, что если на тело не действуют внешние силы или действие их скомпенсировано и одна часть тела начинает вращение в одну сторону, то другая часть должна вращаться в другую сторону, подобно тому как при выбросе горючего из ракеты сама ракета движется в противоположную сторону.

Момент импульса.

Если рассмотреть вращающийся диск, то становится очевидным, что суммарный импульс диска равен нулю, так как любой частице тела соответствует частица, движущаяся с равной по модулю скоростью, но в противоположном направлении (рис. 6.9).

Но диск движется, угловая скорость вращения всех частиц одинакова. Однако ясно, что чем дальше находится частица от оси вращения, тем больше её импульс. Следовательно, для вращательного движения надо ввести ещё одну характеристику, подобную импульсу, — момент импульса.

Моментом импульса частицы, движущейся по окружности, называют произведение импульса частицы на расстояние от неё до оси вращения (рис. 6.10):

Линейная и угловая скорости связаны соотношением v = ωr, тогда

Все точки твёрдого дела движутся относительно неподвижной оси вращения с одинаковой угловой скоростью. Твёрдое тело можно представить как совокупность материальных точек.

Момент импульса твёрдого тела равен произведению момента инерции на угловую скорость вращения:

Момент импульса — векторная величина, согласно формуле (6.3) момент импульса направлен так же, как и угловая скорость.

Основное уравнение динамики вращательного движения в импульсной форме.

Угловое ускорение тела равно изменению угловой скорости, делённому на промежуток времени, в течение которого это изменение произошло: Подставим это выражение в основное уравнение динамики вращательного движения отсюда I(ω₂ — ω₁) = MΔt, или IΔω = MΔt.

Изменение момента импульса равно произведению суммарного момента сил, действующих на тело или систему, на время действия этих сил.

Закон сохранения момента импульса:

Если суммарный момент сил, действующих на тело или систему тел, имеющих неподвижную ось вращения, равен нулю, то изменение момента импульса также равно нулю, т. е. момент импульса системы остаётся постоянным.

Изменение импульса системы равно суммарному импульсу сил, действующих на систему.

Вращающийся фигурист разводит в стороны руки, тем самым увеличивает момент инерции, чтобы уменьшить угловую скорость вращения.

Закон сохранения момента импульса можно продемонстрировать с помощью следующего опыта, называемого «опыт со скамьёй Жуковского». На скамью, имеющую вертикальную ось вращения, проходящую через её центр, встаёт человек. Человек держит в руках гантели. Если скамью заставить вращаться, то человек может изменять скорость вращения, прижимая гантели к груди или опуская руки, а затем разводя их. Разводя руки, он увеличивает момент инерции, и угловая скорость вращения уменьшается (рис. 6.11, а), опуская руки, он уменьшает момент инерции, и угловая скорость вращения скамьи увеличивается (рис. 6.11, б).

Человек может также заставить вращаться скамью, если пойдёт вдоль её края. При этом скамья будет вращаться в противоположном направлении, так как суммарный момент импульса должен остаться равным нулю.

На законе сохранения момента импульса основан принцип действия приборов, называемых гироскопами. Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.

Кинетическая энергия вращающегося твёрдого тела.

Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:

Угловая скорость вращения всех точек тела одинакова, следовательно,

Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид

В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна

В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика