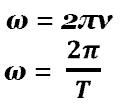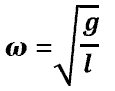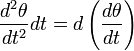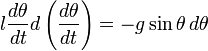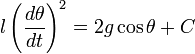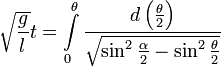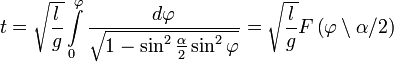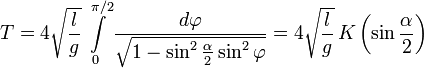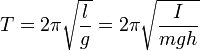Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
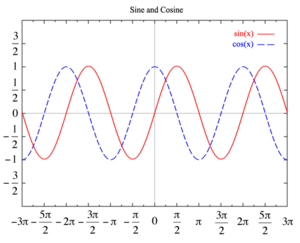
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
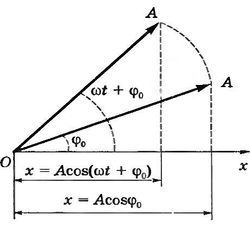
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
— амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий — по начальным значениям координаты и скорости.
к оглавлению ▴
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Видеоурок: Маятник — Физика в опытах и экспериментах
Лекция: Период и частота колебаний
Маятник — это физическое тело, совершающее колебания под действием сил тяжести или упругости.
Рассмотрим два вида маятников: математический и пружинный.

Идеальной системой колебаний является математический маятник. Данная модель состоит из упругой длинной нити с большой жесткостью и небольшого тела на её конце. Если отклонить такой маятник от состояния равновесия всего на 5 градусов или менее, то он будет совершать гармонические колебания.
Гармонические колебания данного тела совершаются благодаря силе натяжения нити и силе тяжести.
Для вывода формул периода математического маятника, следует воспользоваться Вторым законом Ньютона и основными уравнениями механики. В результате этого получим, что период и циклическая частота математического маятника равны:
Отсюда можно сделать вывод, что ни масса тела маятника, ни выбранная амплитуда не влияют на период и частоту колебаний. Они зависят только от длины нити и ускорения свободного падения в данной местности.
Математический маятник используют для регулирования часов в определенной местности в любой точке земного шара, поскольку, мы уже знаем, что ускорение свободного падения на разных частях поверхностей Земли отличается.
Математический маятник также используют для определения местонахождения залежей металлической руды, поскольку в данных местностях ускорение свободного падения увеличивает свое значение.

Пружинный маятник — это тело, прикрепленное к пружине, которое колеблется под действием силы упругости и силы тяжести.
Произведя аналогичные математические выкладки, получим период и циклическую частоту пружинного маятника:
18 Понятие колебательного движения.
Период и частота колебаний
Колеба́ния —
повторяющийся в той или иной степени
во времени
процесс изменения состояний системы
около точки равновесия. Например, при
колебаниях маятника
повторяются отклонения его в ту и другую
сторону от вертикального положения;
при колебаниях в электрическом
колебательном
контуре повторяются величина
и направление тока,
текущего через катушку.
Колебания
почти всегда связаны с попеременным
превращением энергии
одной формы проявления в другую форму.
Колебания
различной физической природы имеют
много общих закономерностей и тесно
взаимосвязаны c волнами.
Поэтому исследованиями этих закономерностей
занимается обобщённая теория
колебаний и волн. Принципиальное
отличие от волн: при колебаниях не
происходит переноса энергии, это, так
сказать, «местные» преобразования
энергии.
Выделение
разных видов колебаний зависит от
подчёркиваемых свойств колеблющихся
систем (осцилляторов)
[править]
По физической природе
-
Механические
(звук,
вибрация) -
Электромагнитные
(свет,
радиоволны,
тепловые) -
Смешанного
типа —
комбинации вышеперечисленных
[править]
По характеру взаимодействия с окружающей
средой
-
Вынужденные —
колебания, протекающие в системе под
влиянием внешнего периодического
воздействия. Примеры: листья на деревьях,
поднятие и опускание руки. При вынужденных
колебаниях может возникнуть явление
резонанса:
резкое возрастание амплитуды колебаний
при совпадении собственной
частоты
осциллятора
и частоты внешнего воздействия. -
Свободные
(или собственные) —
это колебания в системе под действием
внутренних сил, после того как система
выведена из состояния равновесия (в
реальных условиях свободные колебания
всегда затухающие).
Простейшими примерами свободных
колебания являются колебания груза,
прикреплённого к пружине, или груза,
подвешенного на нити. -
Автоколебания —
колебания, при которых система имеет
запас потенциальной
энергии,
расходующейся на совершение колебаний
(пример такой системы — механические
часы).
Характерным отличием автоколебаний
от свободных колебаний является, то
что их амплитуда определяется свойствами
самой системы, а не начальными условиями. -
Параметрические —
колебания, возникающие при изменении
какого-либо параметра колебательной
системы в результате внешнего воздействия. -
Случайные —
колебания, при которых внешняя или
параметрическая нагрузка является
случайным процессом.
[править]
Характеристики
-
Амплитуда —
максимальное отклонение колеблющейся
величины от некоторого усреднённого
её значения для системы,
(м) -
Период —
промежуток времени, через который
повторяются какие-либо показатели
состояния системы (система совершает
одно полное колебание),
(сек) -
Частота —
число колебаний в единицу времени,
(Гц,
сек−1).
Период
колебаний
и
частота
—
обратные величины;
и
В
круговых или циклических процессах
вместо характеристики «частота»
используется понятие круговая
(циклическая)
частота
(рад/сек,
Гц, сек−1),
показывающая число колебаний за 2π
единиц времени:
-
Смещение
— отклонение тела от положения
равновесия. Обозначение Х, Единица
измерения метр. -
Фаза
колебаний —
определяет смещение в любой момент
времени, то есть определяет состояние
колебательной системы.
19 Гармонические
колебания. Векторная диаграмма
гармонического колебания. Циклическая
частота, фаза, начальная фаза
Гармоническое
колебание —
явление периодического изменения
какой-либо величины, при котором
зависимость от аргумента имеет характер
функции синуса или косинуса. Например,
гармонически колеблется величина,
изменяющаяся во времени следующим
образом:
x(t)
= Asin(ωt
+ φ)
или
x(t)
= Acos(ωt
+ φ),
Графики
функций f(x)
= sin(x)
и g(x)
= cos(x)
на декартовой плоскости.
где
х —
значение изменяющейся величины, t —
время, остальные параметры — постоянные:
А —
амплитуда колебаний, ω —
циклическая частота колебаний, (ωt
+ φ) — полная фаза колебаний,
—
начальная фаза колебаний.
Обобщенное
гармоническое колебание в дифференциальном
виде
(Любое
нетривиальное
решение этого дифференциального
уравнения — есть гармоническое колебание
с циклической частотой ω.)
Способ
векторных диаграмм.
Пусть величина х изменяется со временем
по закону
На
плоскости выбирают произвольно
направленную координатную ось Ох.
Из начала координат под углом
равным
начальной фазе колебаний, проводят
вектор
,
модуль которого равен амплитуде
гармонического колебания A (рис. 13.5).
Если вектор
вращается
вокруг точки О с постоянной угловой
скоростью
против
часовой стрелки, то угол
между
вращающимся вектором и осью Ох
в любой момент времени определится
выражением
Проекция
конца вектора
будет
перемещаться по оси Ох
и принимать значения от —А до +А, а
колеблющаяся величина будет изменяться
со временем по закону
Рис.
13.5
Таким
образом, гармоническое колебание можно
представить проекцией на некоторую
произвольно выбранную ось вектора
амплитуды
,
отложенного от произвольной точки оси
под углом
,
равным начальной фазе, и вращающегося
с угловой скоростью
вокруг
этой точки.
Циклическая частота
колебний (ω) — число колебаний за 2π
секунд.
—
связь циклической частоты с частотой
колебаний и периодом.
Циклическая
частота в уравнениях колебаний:
—
циклическая частота колебаний
математического маятника.
Фа́за
колеба́ний —
физическая величина, при заданной
амплитуде
и коэффициенте
затухания,
определяющая состояние колебательной
системы в любой момент времени.[1]
Если колебания системы описываются
синусоидальным (косинусоидальным) или
экспоненциальным законами:
Acos(ωt
+ φ0),
Asin(ωt
+ φ0),
,
то
фаза колебаний определяется как аргумент
периодической функции,
описывающей гармонический колебательный
процесс (ω— угловая
частота
(чем величина выше, тем на большее
значение изменяется угол за ед. времени),
t—
время,
φ0—
(угол в начале колебаний) начальная фаза
колебаний, то есть фаза колебаний в
начальный момент времени t
= 0).
Фаза
обычно выражается в угловых единицах
(радианах,
градусах)
или в циклах
(долях периода):
1
цикл = 2π радиан = 360 градусов.
Строго
говоря, этот термин относится только к
колебаниям, но его также применяют и к
другим периодическим и квазипериодическим
процессам.
20 Гармонические
колебания под действием упругой силы
(вывод закона Гука)
Пружинный
маятник состоит из пружины и массивного
шара, насаженного на горизонтальный
стержень, вдоль которого он может
скользить. Пусть на пружине укреплен
шарик с отверстием, который скользит
вдоль направляющей оси (стержня). На
рис. 7.2,а показано положение шара в
состоянии покоя; на рис. 7.2,б — максимальное
сжатие и на рис. 7.2,в -произвольное
положение шарика.

Под
действием возвращающей силы, равной
силе сжатия, шарик будет совершать
колебания. Сила сжатия F = -kx , где k —
коэффициент жесткости пружины. Знак
минус показывает, что направление силы
F и смещение х противоположны. Потенциальная
энергия сжатой пружины
кинетическая
.
Для
вывода уравнения движения шарика
необходимо связать х и t. Вывод основывается
на законе сохранения энергии. Полная
механическая энергия равна сумме
кинетической и потенциальной энергии
системы. В данном случае :
.
В
положении б)
:
.
Так
как в рассматриваемом движении выполняется
закон сохранения механической энергии,
можно записать:
.
Определим
отсюда скорость:
Но
в свою очередь
и,
следовательно,
.
Разделим
переменные
.
Интегрируя
это выражение, получим:
,
где
—
постоянная интегрирования.
Из
последнего следует, что
|
|
(7.2) |
Сравнивая
(7.1) с (7.2), получаем
|
|
(7.3) |
Таким
образом, под действием упругой силы
тело совершает гармонические колебания.
Силы иной природы, чем упругие, но в
которых выполняется условие F = -kx,
называются квазиупругими. Под действием
этих сил тела тоже совершают гармонические
колебания. При этом:
|
смещение: |
|
|
скорость: |
|
|
ускорение: |
|
Сила
упругости, возникающая в теле при его
деформации, прямо пропорциональна
величине этой деформации
Для
тонкого растяжимого стержня закон Гука
имеет вид:
Здесь
F — сила натяжения стержня, Δl —
абсолютное удлинение (сжатие) стержня,
а k называется коэффициентом
упругости (или жёсткости).
Коэффициент
упругости зависит как от свойств
материала, так и от размеров стержня.
Можно выделить зависимость от размеров
стержня (площади поперечного сечения
S и длины L) явно, записав коэффициент
упругости как
Величина
E называется Модулем
упругости первого рода или модулем Юнга
и является механической характеристикой
материала.
Если
ввести относительное удлинение
и
нормальное напряжение в поперечном
сечении
то
закон Гука в относительных единицах
запишется как
В
такой форме он справедлив для любых
малых объёмов вещества.
Также
при расчёте прямых стержней применяют
запись закона Гука в относительной
форме
Следует
иметь в виду, что закон Гука выполняется
только при малых деформациях. При
превышении предела
пропорциональности связь между
напряжениями и деформациями становится
нелинейной. Для многих сред закон Гука
неприменим даже при малых деформациях.
21 Циклическая частота
и период колебаний под действием упругой
силы. Энергия колебания.
ЧАСТИЧНО НЕ НАЙДЕНО
При
механических
колебаниях колеблющееся тело (или
материальная точка) обладает кинетической
и потенциальной энергией. Кинетическая
энергия тела W:
(Скорость
тела v
= ds/dt)
Для
вычисления потенциальной энергии тела
воспользуемся самой общей формулой,
связывающей силу и потенциальную энергию
тела в поле этой силы:

где
U — потенциальная энергия, набираемая
(или теряемая) телом, движущимся в силовом
поле F от точки 0 (точки, в которой
потенциальная энергия принимается
равной 0) до точки х.
Для
силы, линейно зависящей от смещения
(как в случае наших механических
маятников, такие силы носят общее
название квазиупругих сил) мы имеем:
|
для |
1.
Полная механическая энергия тела не
изменяется при колебаниях:
2.
Частота колебаний кинетической и
потенциальной энергии в 2 раза больше
частоты колебаний маятника.
3.
Колебания кинетической и потенциальной
энергии сдвинуты друг относительно
друга по фазе на
(на полпериода). Когда кинетическая
энергия достигает максимума, потенциальная
— минимума (нуля) и наоборот. Энергия при
колебаниях постоянно перекачивается
из потенциальной в кинетическую и
обратно.
В
случае электрических колебаний энергия
в конуре представляет собой сумму
энергии электрического поля, запасенной
между обкладками конденсатора, и энергии
магнитного поля, запасенной в катушке
с индуктивностью. Вычислим обе
составляющие.
Сравнивая
эти формулы, можно сделать следующие
выводы:
1.
Полная энергия в контуре остается
неизменной:
2.
Частота колебаний энергий в 2 раза
превосходит частоту колебаний заряда
и тока в контуре.
3. Электрическая и
магнитная энергии сдвинуты по фазе на
полпериода друг относительно друга;
происходит непрерывное перекачивание
энергии из одной формы в другую и обратно.
Поскольку
в контуре происходят колебания
электрической и магнитной энергий,
электрический колебательный контур
также называют электромагнитным.
22 Сложение одинокого
направленных гармонических колебаний.
Колеблющееся
тело может принимать участие в нескольких
колебательных процессах, тогда следует
найти результирующее колебание, другими
словами, колебания необходимо сложить.
В данном разделе будем складывать
гармонические колебания одного
направления и одинаковой частоты
применяя
метод вращающегося вектора амплитуды,
построим графически векторные диаграммы
этих колебаний (рис. 1). Tax как векторы A1
и A2
вращаются с одинаковой угловой скоростью
ω0,
то разность фаз (φ2
— φ1)
между ними будет оставаться постоянной.
Значит, уравнение результирующего
колебания будет
(1)
В формуле (1) амплитуда А и начальная
фаза φ соответственно определяются
выражениями
(2)
Значит,
тело, участвуя в двух гармонических
колебаниях одного направления и
одинаковой частоты, совершает при этом
также гармоническое колебание в том же
направлении и с той же частотой, что и
складываемые колебания. Амплитуда
результирующего колебания зависит от
разности фаз (φ2
— φ1)
складываемых колебаний.

Рис.1
Исследуем
выражение (2) в зависимости от разности
фаз (φ2
— φ1):
1) φ2
— φ1
= ±2mπ (m = 0, 1, 2, …), тогда A=A1+A2,
т. е. амплитуда результирующего колебания
А будет равна сумме амплитуд складываемых
колебаний;
2) φ2
— φ1
= ±(2m+1)π (m = 0, 1, 2, …), тогда A=|A1–A2|,
т. е. амплитуда результирующего колебания
будет равна разности амплитуд складываемых
колебаний.
Для практики представляет
особый интерес случай, когда два
складываемых гармонических колебания
одинакового направления мало отличаются
по частоте. После сложения этих колебаний
получаются колебания с периодически
изменяющейся амплитудой. Периодические
изменения амплитуды колебания, которые
возникают при сложении двух гармонических
колебаний с близкими частотами, называются
биениями.
Пусть амплитуды складываемых
колебаний равны А, а частоты равны ω и
ω+Δω, причем Δω<<ω. Выберем начало
отсчета так, чтобы начальные фазы обоих
колебаний были равны нулю:
Складывая
эти выражения и учитывая, что во втором
сомножителе Δω/2<<ω, получим
(3)
Результирующее колебание (3) можно
считать как гармоническое с частотой
ω , амплитуда Аσ
которого изменяется по следующему
периодическому закону:
(4)
Частота изменения Аσ
в два раза больше частоты изменения
косинуса (так как берется по модулю), т.
е. частота биений равна разности частот
складываемых колебаний:
Период
биений
Вид
зависимости (3) показан на рис. 2, где
сплошные жирные линии представляют
график результирующего колебания (3), а
огибающие их линии — график медленно
меняющейся согласно уравнению (4)
амплитуды.

Рис.2
Нахождение
частоты тона (звука определенной высоты)
биений между эталонным и измеряемым
колебаниями — наиболее часто используемый
на практике метод сравнения измеряемой
величины с эталонной. Метод биений
применяется для настройки музыкальных
инструментов, анализа слуха и т. д.
При
исследовании сложного колебательного
процесса нужно знать, что любые сложные
периодические колебания s=f(t) можно
представить в виде суперпозиции
(наложения) одновременно совершающихся
гармонических колебаний с различными
амплитудами, начальными фазами, а также
частотами, которые кратны циклической
частоте ω0
:
(5)
Представление в виде (5) любой
периодической функции связывают с
понятием гармонического
анализа сложного периодического
колебания,
или разложения
Фурье.
Слагаемые ряда Фурье, которые определяют
гармонические колебания с частотами
ω0,
2ω0,
3ω0,
…, называются первой
(или основной),
второй,
третьей
и т. д. гармониками
сложного периодического колебания.
23 Колебания физического
маятника.
Физический маятник
— осциллятор,
представляющий собой твёрдое
тело, совершающее колебания
в поле
каких-либо сил
относительно точки, не являющейся
центром
масс этого тела, или неподвижной
оси, перпендикулярной направлению
действия сил и не проходящей через центр
масс этого тела.
Определения
-
—
угол отклонения маятника от равновесия; -
—
начальный угол отклонения маятника; -
—
масса маятника; -
—
расстояние от точки подвеса до центра
тяжести маятника; -
—
радиус инерции относительно оси,
проходящей через центр тяжести. -
—
ускорение свободного падения.
Момент
инерции относительно оси,
проходящей через точку подвеса:
.
[Править] Дифференциальное уравнение движения физического маятника
Основная
статья: Приведённая
длина
Пренебрегая
сопротивлением среды, дифференциальное
уравнение колебаний физического маятника
в поле силы тяжести записывается
следующим образом:
.
Полагая
,
предыдущее уравнение можно переписать
в виде:
.
Последнее
уравнение аналогично уравнению колебаний
математического
маятника длиной
.
Величина
называется
приведённой
длиной физического маятника.
[Править] Центр качания физического маятника
Центр
качания — точка, в которой надо
сосредоточить всю массу физического
маятника, чтобы его период колебаний
не изменился.
Поместим
на луче,
проходящем от точки подвеса через центр
тяжести точку на расстоянии
от
точки подвеса. Эта точка и будет центром
качания маятника.
Действительно,
если всю массу сосредоточить в центре
качания, то центр качания будет совпадать
с центром масс. Тогда момент инерции
относительно оси подвеса будет равен
,
а момент
силы тяжести относительно той
же оси
.
Легко заметить, что уравнение движения
не изменится.
[править]
Теорема Гюйгенса
[править]
Формулировка
Если
физический маятник подвесить за центр
качания, то его период колебаний не
изменится, а прежняя точка подвеса
сделается новым центром качания.
[править]
Доказательство
Вычислим
приведенную длину для нового маятника:
.
Совпадение
приведённых длин для двух случаев и
доказывает утверждение, сделанное в
теореме.
[править]
Период колебаний физического маятника
Для
того, чтобы найти период колебаний
физического маятника, необходимо решить
уравнение качания. Для этого умножим
левую часть этого уравнения на
,
а правую часть на
.
Тогда:
.
Интегрируя
это уравнение, получаем.
,
где
произвольная
постоянная. Её можно найти из граничного
условия, что в моменты
.
Получаем:
.
Подставляем и преобразовываем получившееся
уравнение:
.
Отделяем
переменные и интегрируем это уравнение:
.
Удобно
сделать замену переменной, полагая
.
Тогда искомое уравнение принимает вид:
.
Здесь
—
нормальный
эллиптический интеграл Лежандра 1-го
рода. Для периода колебаний
получаем формулу:
.
Здесь
—
полный
нормальный эллиптический интеграл
Лежандра 1-го рода.
[Править] Период малых колебаний физического маятника
Если
амплитуда колебаний
мала,
то корень в знаменателе эллиптического
интеграла приближенно равен единице.
Такой интеграл легко берется, и получается
хорошо известная формула малых колебаний:
.
24 Колебания
математического маятника
Математи́ческий
ма́ятник —
осциллятор,
представляющий собой механическую
систему,
состоящую из материальной
точки,
находящейся на невесомой
нерастяжимой
нити или на невесомом стержне
в однородном поле сил тяготения.
Период
малых собственных колебаний
математического маятника длины l
неподвижно подвешенного в однородном
поле тяжести с ускорением
свободного падения
g
равен
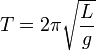
и
не зависит[1]
от амплитуды
и массы
маятника.
Плоский
математический маятник со стержнем —
система с одной степенью
свободы.
Если же стержень заменить на растяжимую
нить, то это система с двумя степенями
свободы со связью. Пример школьной
задачи, в которой важен переход от одной
к двум степеням свободы.
При
малых
колебаниях
физический
маятник
колеблется так же, как математический
с приведённой
длиной.
Уравнение
колебаний маятника
Колебания
математического маятника описываются
обыкновенным
дифференциальным уравнением
вида
где
ω ― положительная константа, определяемая
исключительно из параметров маятника.
Неизвестная функция x(t)
― это угол отклонения маятника в момент
t
от нижнего положения равновесия,
выраженный в радианах;
,
где L
― длина подвеса, g
― ускорение
свободного падения.
Уравнение малых колебаний маятника
около нижнего положения равновесия
(т. н. гармоническое уравнение) имеет
вид:
.
[править]
Решения уравнения движения
[править]
Гармонические колебания
Маятник,
совершающий малые колебания, движется
по синусоиде. Поскольку уравнение
движения является обыкновенным ДУ
второго порядка, для определения закона
движения маятника необходимо задать
два начальных условия — координату
и скорость, из которых определяются две
независимых константы:
где
A —
амплитуда
колебаний маятника, θ0 —
начальная фаза
колебаний, ω — циклическая
частота,
которая определяется из уравнения
движения. Движение, совершаемое маятником,
называется гармоническими
колебаниями
[править]
Нелинейный маятник
Для
маятника, совершающего колебания с
большой амплитудой, закон движения
более сложен:
где
—
это синус
Якоби.
Для
он
является периодической функцией, при
малых
совпадает
с обычным тригонометрическим синусом.
Параметр
определяется
выражением
где
—
энергия маятника в единицах t−2.
Период
колебаний нелинейного маятника
где
K — эллиптический интеграл первого
рода.
[править]
Движение по сепаратрисе
Движение
маятника по сепаратрисе является
непериодическим. В бесконечно далёкий
момент времени он начинает падать из
крайнего верхнего положения в какую-то
сторону с нулевой скоростью, постепенно
набирает её, и останавливается,
возвратившись в исходное положение.
25 Затухающие колебания.
Зависимость амплитуды от времени.
Затухающие колебания —
колебания, энергия которых уменьшается
с течением времени. Бесконечно длящийся
процесс вида
в
природе невозможен. Свободные колебания
любого осциллятора рано или поздно
затухают и прекращаются. Поэтому на
практике обычно имеют дело с затухающими
колебаниями. Они характеризуются тем,
что амплитуда колебаний A является
убывающей функцией. Обычно затухание
происходит под действием сил сопротивления
среды, наиболее часто выражаемых линейной
зависимостью от скорости колебаний
или
её квадрата.
Пускай
имеется система, состоящая из пружины
(подчиняющейся закону
Гука), один конец которой жёстко
закреплён, а на другом находится тело
массой m. Колебания совершаются в
среде, где сила сопротивления
пропорциональна скорости с коэффициентом
c (см. вязкое
трение).
Тогда
второй
закон Ньютона для рассматриваемой
системы запишется так:
где
Fc — сила сопротивления,
Fy — сила упругости
Fc
= − cv, Fy = − kx, то
есть
ma + cv
+ kx = 0
или
в дифференциальной форме
где
k — коэффициент упругости в законе
Гука, c — коэффициент
сопротивления, устанавливающий
соотношение между скоростью движения
грузика и возникающей при этом силой
сопротивления.
Для
упрощения вводятся следующие обозначения:
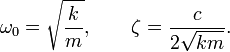
Величину
ω называют собственной частотой системы,
ζ — коэффициентом затухания.
Тогда
дифференциальное уравнение принимает
вид
Сделав
замену x = eλt,
получают характеристическое
уравнение
Корни
которого вычисляются по следующей
формуле
Математическим маятником называют материальную точку (тело небольших размеров), подвешенную на тонкой невесомой нерастяжимой нити или на невесомом стержне.
Рис. (1). Силы, действующие на материальную точку в положении равновесия и при отклонении от положения равновесия
В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое.
При отклонении материальной точки от положения равновесия на малый угол
α
на тело будет действовать возвращающая сила (F), которая является тангенциальной составляющей силы тяжести:
Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки уменьшаются. В момент прохождения положения равновесия угол отклонения
α
(=0), тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна.
Далее материальная точка проходит по инерции положение равновесия и, двигаясь далее, сбавляет скорость. В крайнем положении материальная точка останавливается и затем начинает двигаться в обратном направлении.
Период малых собственных колебаний математического маятника длины (l), неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения (g), равен
Обрати внимание!
Период колебаний математического маятника не зависит от амплитуды колебаний и массы груза.
Наиболее известным практическим использованием маятника является применение его в часах для измерения времени. Впервые это сделал голландский физик X. Гюйгенс.
Рис. (2). Колебания маятника часов
Поскольку период колебаний маятника зависит от ускорения свободного падения (g), то часы, которые идут верно в Москве, будут идти вперёд в Санкт-Петербурге. Чтобы эти часы шли верно в Санкт-Петербурге, приведённую длину их маятника нужно увеличить.
В геологии маятник применяют для опытного определения числового значения ускорения свободного падения (g) в разных точках земной поверхности. Для этого по достаточно большому числу колебаний маятника в том месте, где измеряют (g), находят период его колебаний, а затем вычисляют ускорение свободного падения, выразив его из формулы периода маятника.
Заметное отклонение величины (g) от нормы для какой-либо местности называют гравитационной аномалией.
Определение аномалий помогает находить залежи полезных ископаемых.
Опыт показывает, что качающийся маятник сохраняет плоскость, в которой происходят его колебания. Это означает, что если привести в движение маятник, установленный на диске центробежной машины, а диск заставить вращаться, то плоскость качания маятника относительно комнаты изменяться не будет. Это позволяет с помощью опыта обнаружить вращение Земли вокруг своей оси.
В (1850) г. Ж. Фуко подвесил маятник под куполом высокого здания так, что острие маятника при качании оставляло след на песке, насыпанном на полу. Оказалось, что при каждом качании острие оставляет на песке новый след. Таким образом, опыт Фуко показал, что Земля вращается вокруг своей оси. В условиях вращения Земли при достаточно большой нити подвеса плоскость, в которой маятник совершает колебания, медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли.
При исследовании гармонических колебаний твердого тела, которое не моделируют в виде материальной точки, рассматривают физический маятник.
Источники:
Рис. 1. Силы, действующие на материальную точку в положении равновесия и при отклонении от положения равновесия. . © ЯКласс.
Рис. 2. Колебания маятника часов. ЮК, Public domain, via Wikimedia Commons. 2021-08-29.
Периоды малых колебаний математического и пружинного маятников
Математическим маятником называется груз, подвешенный на нити, длина которой намного больше размера груза, а масса пренебрежимо мала по сравнению с массой груза.
Расчеты показывают, что
период малых колебаний математического маятника 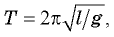
Например, если длина нити равна 1 м, период колебаний равен примерно 2 с.
Поскольку период колебаний математического маятника зависит от значения ускорения свободного падения, с помощью маятника можно производить очень точные измерения величины 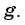
период малых колебаний математического маятника 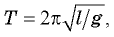
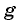
Механика.
2014