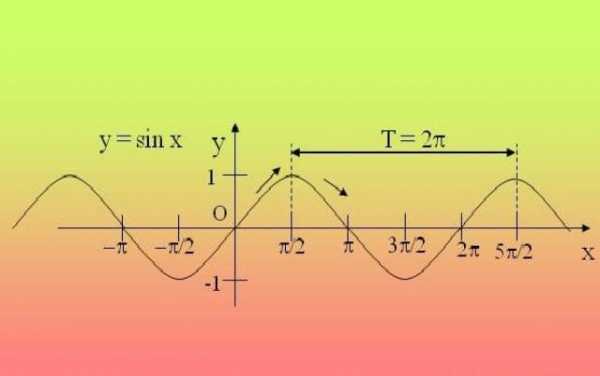
Как найти период математики - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

$[{T_1} = frac{T}{{left| k right|}}]$

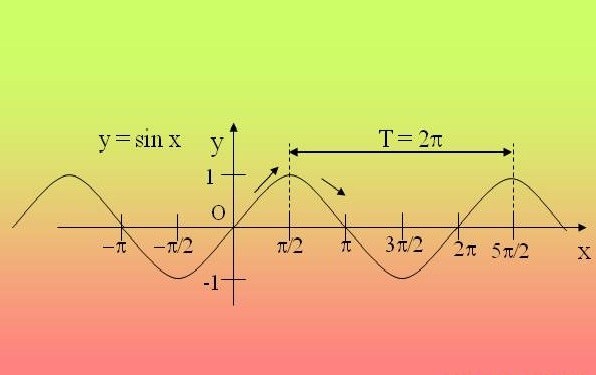
где T — период функции y=f(x). Эта формула позволяет быстро найти период тригонометрических функций такого вида. Для функций y=sin x и y=cos x наименьший положительный период T=2п, для y=tg x и y=ctg x T=п. Рассмотрим на конкретных примерах, как найти период функции, используя данную формулу.

Найти период функции:

1) y=5sin(3x-п/8).

Здесь А=5, k=3, b=-п/8. Для нахождения периода нам нужно только k — число, стоящее перед иксом. Поскольку период синуса T=2п, то период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| 3 right|}} = frac{{2pi }}{3}.]$

$[2)y = frac{2}{7}cos (frac{pi }{5} - frac{x}{{11}})]$

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

$[{T_1} = frac{T}{{left| k right|}} = frac{{2pi }}{{left| { - frac{1}{{11}}} right|}} = 2pi cdot 11 = 22pi .]$

$[3)y = 0,3tg(frac{{5x}}{9} - frac{pi }{7})]$

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {frac{5}{9}} right|}} = frac{{9pi }}{5}.]$

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

$[{T_1} = frac{T}{{left| k right|}} = frac{pi }{{left| {0,4} right|}} = frac{{10pi }}{4} = frac{{5pi }}{2}.]$

Источник

Как определить периодичность функции

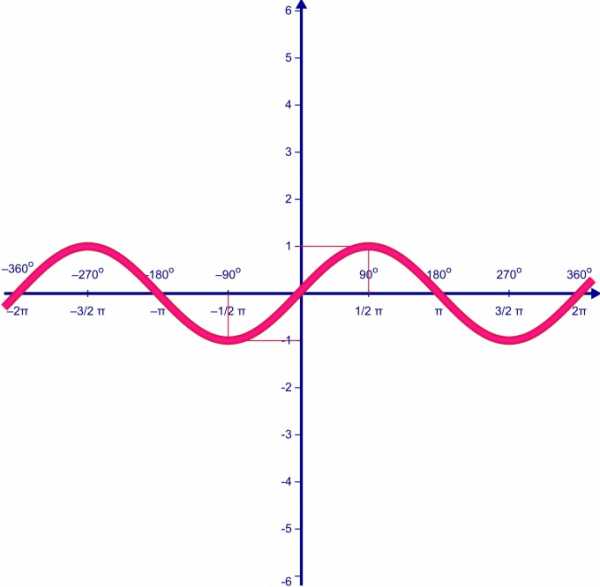
По школьным урокам математики каждый помнит график синуса, равномерными волнами уходящий вдаль. Аналогичным свойством — повторяться через определенный промежуток — обладают и многие другие функции. Они называются периодическими. Периодичность — очень важное свойство функции, часто встречающееся в различных задачах. Поэтому полезно уметь определять, является ли функция периодической.

Инструкция

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.

Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете график функции по горизонтали именно в столько раз

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Однако если соотношение периодов иррационально, то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.

Источники:

Теоретические сведения о функциях

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Это очень просто

Время на прочтение
2 мин

Количество просмотров 19K

Рассмотрим следующую задачу. Найти период дроби 1/81. Уверяю, что для решения не потребуется ни калькулятор, ни деление столбиком. Для начала вспомним чему равно 81*(Период). Пусть длина периода n, тогда исходная дробь запишется как:

$frac{1}p=frac{Период}{10^n}+frac{Период}{10^{2n}}+frac{Период}{10^{3n}}+...$

Перепишем данное представление в следующем виде:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotleft(frac{Период}{10^{n}}+frac{Период}{10^{2n}}+..right)$

Последнее выражение можно представить так:

$frac{1}p=frac{Период}{10^n}+frac{1}{10^n} cdotfrac{1}p$

Ну а теперь то соотношение, которое мы искали:

Для нашего случая это тождество будет следующим:

Разделим левую и правую часть на 9, получим:

Первое число, составленное из одних единиц, которое делится на 9 равно 111111111, это следует из признака делимости на 9. Делить будем через сумму цифр исходного числа. Двигаемся слева направо, складываем цифры делимого и на каждом шаге записываем полученную сумму. Результат работы данного алгоритма — число 12345678,9999… Здесь надо пояснить, что когда мы достигаем крайней правой цифры, то ставим запятую и полученную сумму цифр исходного числа дублируем как бесконечную десятичную дробь. Вспоминаем, что 0,999…=1 и получаем ответ, который мы искали 12345679. Если рассмотреть более общую задачу нахождения периода дроби $frac{1}{9^n}$ , то окажется, что период такой дроби имеет длину ${9^{n-1}}$ и если известен период для случая n-1, то следующий равен произведению данного периода на число вида 11111… (повторяется ${9^{n-1}}$ раз)22222… (повторяется ${9^{n-1}}$ раз)33333… (повторяется ${9^{n-1}}$ раз). Самая правая секция будет иметь вид 8888..889. Последняя цифра девятка.
И еще одно наблюдение, теперь для дробей вида $frac{1}{11^{n}}$ . В этом случае длина периода равна $2cdot{11^{n-1}}$ . И если известен период для случая n-1, то следующий период равен произведению данного периода на число, составленное из 10 блоков, где длина каждого блока $2cdot{11^{n-2}}$ . Блоки имеют следующую структуру:
09090909…
18181818…
27272727…
36363636…
…
последний блок 90909091. Для $frac{1}{11}$ период 09, для $frac{1}{11^{2}}$ период будет 09182736455463728191*9=0082644628099173553719.
Проверил формулу для $frac{1}{11^{3}}$ . Получил

75131480090157776108189331329827197595792637114951164537941397445529676934635612
32156273478587528174305033809166040570999248685199098422238918106686701728024042
0736288504883546205860255447032306536438767843726521412471825694966190833959429,

что совпадает с периодом без ведущих нулей.

Приведу код процедур, которые я использовал для проверки своих выводов.

Function GreatestCommonDivisor(x,y)

    if x=y then
        return x;
    endif;  

    a=min(x,y);
    if a=1 then
        return 1;
    endif;  
    b=x+y-a;

    while TRUE do
     c=b%a; 
     if c=0 then
         return a;
     endif;  
     b=a;
     a=c;
    enddo;

EndFunction

Function NumeratorFractionPeriod(numerator,denumerator)

    // дробь a/b

    a=numerator;
    b=denumerator;

    while b%2=0 do
        b=b/2;
        a=a*5;
    enddo;  

    while b%5=0 do
        b=b/5;
        a=a*2;
    enddo;  
    //наибольший общий делитель
    c=GreatestCommonDivisor(a,b);
    a=a/c;
    b=b/c;

    if b=1 then
        Period=string(a);
        return Period;
    endif;

    if a>b then
        Period=string((a-a%b)/b);
        a=a%b;
        if a=0 then
            return Period;
        endif;  
        Period=Period+"(";
    else
        Period="(";
    endif;      

    while a%10=0 do
        a=a/10;
    enddo;  

    i=a;
    while TRUE do
        j=0;
        while i<b do
            i=i*10;
            j=j+1;
            if j>1 then
             Period=Period+"0";
            endif; 
        enddo;  

        check=i-a;
        if (check%b)=0 then
            Period=Period+(check)/b;
            break;
        else
            j=i%b;
            Period=Period+(i-j)/b;
            i=j;
        endif;    
    enddo;

    return Period+")";
EndFunction

Источник

Совет 1: Как обнаружить период тригонометрической функции

Тригонометрические функции периодичны , то есть повторяются через определенный период. Вследствие этому довольно изучать функцию на этом интервале и распространить обнаруженные свойства на все остальные периоды.

Инструкция

1. Если вам дано примитивное выражение, в котором присутствует лишь одна тригонометрическая функция (sin, cos, tg, ctg, sec, cosec), причем угол внутри функции не умножен на какое-нибудь число, а она сама не возведена в какую-нибудь степень – воспользуйтесь определением. Для выражений, содержащих sin, cos, sec, cosec отважно ставьте период 2П, а если в уравнении есть tg, ctg – то П. Скажем, для функции у=2 sinх+5 период будет равен 2П.

2. Если угол х под знаком тригонометрической функции умножен на какое-нибудь число, то, дабы обнаружить период данной функции, поделите типовой период на это число. Скажем, вам дана функция у= sin 5х. Типовой период для синуса – 2П, поделив его на 5, вы получите 2П/5 – это и есть желанный период данного выражения.

3. Дабы обнаружить период тригонометрической функции, возведенной в степень, оцените четность степени. Для четной степени уменьшите типовой период в два раза. Скажем, если вам дана функция у=3 cos^2х, то типовой период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите внимание, функции tg, ctg в всякий степени периодичны П.

4. Если вам дано уравнение, содержащее произведение либо частное 2-х тригонометрических функций, вначале обнаружьте период для всей из них отдельно. После этого обнаружьте минимальное число, которое умещало бы в себе целое число обоих периодов. Скажем, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое дозволено уместить оба этих периода, это 2П, таким образом, желанный период – 2П.

5. Если вы затрудняетесь делать предложенным образом либо сомневаетесь в результате, попытайтесь делать по определению. Возьмите в качестве периода функции Т, он огромнее нуля. Подставьте в уравнение взамен х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром либо числом. В итоге вы обнаружите значение тригонометрической функции и сумеете подобрать наименьший период. Скажем, в итоге облегчения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, равно 2П, это и будет результат задачи.

Совет 2: Как находить период функции

Периодической функцией именуется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции именуется число, при добавление которого к доводу функции значение функции не меняется.

Вам понадобится

Знания по элементарной математике и началам обзора.

Инструкция

1. Обозначим период функции f(x) через число К. Наша задача обнаружить это значение К. Для этого представим, что функция f(x), пользуясь определением периодической функции, приравняем f(x+K)=f(x).

2. Решаем полученное уравнение касательно неведомой K, так, как словно x – константа. В зависимости от значения К получится несколько вариантов.

3. Если K>0 – то это и есть период вашей функции.Если K=0 – то функция f(x) не является периодической.Если решение уравнения f(x+K)=f(x) не существует ни при каком K не равном нулю, то такая функция именуется апериодической и у неё тоже нет периода.

Видео по теме

Обратите внимание!
Все тригонометрические функции являются периодическими, а все полиномиальные со степенью огромнее 2 – апериодическими.

Полезный совет
Периодом функции, состоящей из 2-х периодический функций, является Наименьшее всеобщее кратное периодов этих функций.

Совет 3: Как решать тригонометрические уравнения

Тригонометрические уравнения – это уравнения, которые содержат в себе тригонометрические функции неведомого довода (для примера: 5sinx-3cosx =7). Дабы обучиться решать их – необходимо знать некоторые для этого способы.

Инструкция

1. Решение таких уравнения состоит из 2-х этапов.Первое – реформирование уравнения для приобретения его простейшего вида. Простейшими тригонометрическими уравнениями именуются такие: Sinx=a; Cosx=a и т.д.

2. Второе – это решение полученного простейшего тригонометрического уравнения. Существует основные способы решения уравнений такого вида:Решение алгебраическим способом. Данный способ классно знаменит из школы, с курса алгебры. По иному называют способом замены переменной и подстановки. Применяя формулы приведения, преобразуем, делаем замену, позже чего находим корни.

3. Разложение уравнения на множители. Вначале переносим все члены налево и раскладываем на множители.

4. Приведение уравнение к однородному. Однородными уравнениями называют уравнения, если все члены одной и той же степени и синус, косинус одного и того же угла.Дабы его решить, следует: вначале перенести все его члены из правой части в левую часть; перенести все всеобщие множители за скобки; приравнять множители и скобки нулю; приравненные скобки дают однородное уравнение меньшей степени, что следует поделить на cos ( либо sin ) в старшей степени; решить полученное алгебраическое уравнение касательно tan.

5. Дальнейший способ – переход к половинному углу. Скажем, решить уравнение: 3 sin x – 5 cos x = 7.Переходим к половинному углу: 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ? ( x / 2 ) + 5 sin ? ( x / 2 ) = 7 sin ? ( x / 2 ) + 7 cos ? ( x/ 2 ) , позже чего все члены сводим в одну часть (отличнее в правую) и решаем уравнение.

6. Вступление вспомогательного угла. Когда мы заменяем целое значение cos(а) либо sin(а). Знак «а» – вспомогательный угол.

7. Способ реформирования произведения в сумму. Здесь нужно применять соответствующие формулы. Скажем дано: 2 sin x · sin 3x = cos 4x.Решим ее, преобразовав левую часть в сумму, то есть:cos 4x – cos 8x = cos 4x ,cos 8x = 0 ,8x = p / 2 + pk ,x = p / 16 + pk / 8.

8. Конечный способ, называемый многофункциональной подстановкой. Мы преобразовываем выражение и делаем замену, скажем Cos(x/2)=u, позже чего решаем уравнение с параметром u. При приобретении итога переводим значение в обратное.

Видео по теме

Совет 4: Как обнаружить период функции

Если рассматривать точки на окружности, то точки x, x + 2π, x + 4π и т.д. совпадают друг с ином. Таким образом, тригонометрические функции на прямой периодически повторяют свое значение. Если знаменит период функции , дозволено возвести функцию на этом периоде и повторить ее на других.

Инструкция

1. Период – это число T, такое что f(x) = f(x+T). Дабы обнаружить период, решают соответствующее уравнение, подставляя в качестве довода x и x+T. При этом пользуются теснее знаменитыми периодами для функций. Для функций синуса и косинуса период составляет 2π, а для тангенса и котангенса – π.

2. Пускай дана функция f(x) = sin^2(10x). Разглядите выражение sin^2(10x) = sin^2(10(x+T)). Воспользуйтесь формулой для понижения степени: sin^2(x) = (1 – cos 2x)/2. Тогда получите 1 – cos 20x = 1 – cos 20(x+T) либо cos 20x = cos (20x+20T). Зная, что период косинуса равен 2π, 20T = 2&#960. Значит, T = π/10. Т – минимальный правильный период, а функция будет повторяться и через 2Т, и через 3Т, и в иную сторону по оси: -T, -2T и т.д.

Полезный совет
Пользуйтесь формулами для понижения степени функции. Если вам теснее знамениты периоды каких-нибудь функций, пробуйте свести имеющуюся функцию к вестимым.

Совет 5: Как изучать функцию на четность

Изыскание функции на четность и нечетность помогает строить график функции и постигать нрав ее поведения. Для этого изыскания нужно сравнить данную функцию, записанную для довода “х” и для довода “-х”.

Инструкция

1. Запишите функцию, изыскание над которой нужно провести, в виде y=y(x).

2. Замените довод функции на “-х”. Подставьте данный довод в функциональное выражение.

3. Упростите выражение.

4. Таким образом, вы получили одну и ту же функцию, записанную для доводов “х” и “-х”. Посмотрите на две эти записи.Если y(-x)=y(x), то это четная функция.Если y(-x)=-y(x), то это нечетная функция.Если же про функцию невозможно сказать, что y(-x)=y(x) либо y(-x)=-y(x), то по свойству четности это функция всеобщего вида. То есть, она не является ни четной, ни нечетной.

5. Запишите сделанные вами итоги. Сейчас вы можете их применять в построении графика функции либо же в будущем аналитическом изыскании свойств функции.

6. Говорить о четности и нечетности функции дозволено также и в том случае, когда теснее задан график функции. Скажем, график послужил итогом физического эксперимента.Если график функции симметричен касательно оси ординат, то y(x) – четная функция.Если график функции симметричен касательно оси абсцисс, то x(y) – четная функция. x(y) – функция, обратная функции y(x).Если график функции симметричен касательно начала координат (0,0), то y(x) – нечетная функция. Нечетной будет также обратная функция x(y).

7. Значимо помнить, что представление о четности и нечетности функции имеет прямую связь с областью определения функции. Если, скажем, четная либо нечетная функция не существует при х=5, то она не существует и при х=-5, чего невозможно сказать про функцию всеобщего вида. При установлении четности и нечетности обращайте внимание на область определения функции.

8. Изыскание функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции довольно разглядеть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает значения от А до В, то те же значения она будет принимать и при x<0.Для нахождения множества значений, принимаемых нечетной функцией, тоже довольно разглядеть только одну часть функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).

Совет 6: Как решать тригонометрические функции

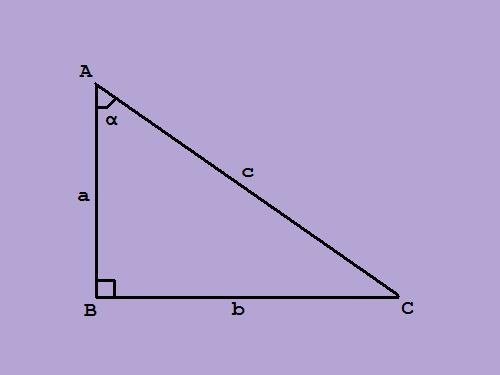
«Тригонометрическими» когда-то стали называть функции, которые определяются зависимостью острых углов в прямоугольном треугольнике от длин его сторон. К таким функциям относят в первую очередь синус и косинус, во вторую – обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Положительнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.

Инструкция

1. Если довод тригонометрической функции неведом, то вычислить ее значение дозволено косвенным методом исходя из определений этих функций. Для этого требуется знать длины сторон треугольника, тригонометрическую функцию для одного из углов которого требуется вычислить. Скажем, по определению синус острого угла в прямоугольном треугольнике – это отношение длины противолежащего этому углу катета к длине гипотенузы. Из этого вытекает, что для нахождения синуса угла довольно знать длины этих 2-х сторон. Схожее определение гласит, что синусом острого угла является отношение длины прилежащего к этому углу катета к длине гипотенузы. Тангенс острого угла дозволено вычислить, поделив длину противолежащего ему катета на длину прилежащего, а котангенс требует деления длины прилежащего катета к длине противолежащего. Для вычисления секанса острого угла нужно обнаружить отношение длины гипотенузы к длине прилежащего к необходимому углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.

2. Если же довод тригонометрической функции вестим, то знать длины сторон треугольника не требуется – дозволено воспользоваться таблицами значений либо калькуляторами тригонометрических функций. Такой калькулятор есть среди стандартных программ операционной системы Windows. Для его запуска дозволено нажать сочетание клавиш Win + R, ввести команду calc и щелкнуть кнопку «OK». В интерфейсе программы следует раскрыть раздел «Вид» и предпочесть пункт «Инженерный» либо «Ученый». Позже этого дозволено вводить довод тригонометрической функции. Для вычисления функций синус, косинус и тангенс довольно позже ввода значения щелкнуть по соответствующей кнопке интерфейса (sin, cos, tg), а для нахождения обратных им арксинуса, арккосинуса и арктангенса следует заблаговременно поставить отметку в чекбоксе Inv.

3. Есть и альтернативные методы. Один из них – перейти на сайт поисковой системы Nigma либо Google и ввести в качестве поискового запроса надобную функцию и ее довод (скажем, sin 0.47). Эти поисковики имеют встроенные калькуляторы, следственно позже отправки такого запроса вы получите значение введенной вами тригонометрической функции.

Видео по теме

Совет 7: Как обнаружить значение тригонометрических функции

Тригонометрические функции сначала появились как инструменты абстрактных математических вычислений зависимостей величин острых углов в прямоугольном треугольнике от длин его сторон. Теперь они дюже обширно используются как в научных, так и в технических областях человеческой деятельности. Для утилитарных вычислений тригонометрических функций от заданных доводов дозволено применять различные инструменты – ниже описано несколько особенно доступных из них.

Инструкция

1. Воспользуйтесь, скажем, устанавливаемой по умолчанию совместно с операционной системой программой-калькулятором. Она открывается выбором пункта «Калькулятор» в папке «Служебные» из подраздела «Типовые», размещенного в раздел «Все программы». Данный раздел дозволено обнаружить, открыв щелчком по кнопке «Пуск» основное меню операционной системы. Если вы используете версию Windows 7, то имеете вероятность примитивно ввести слово «Калькулятор» в поле «Обнаружить программы и файлы» основного меню, а после этого щелкнуть по соответствующей ссылке в итогах поиска.

2. Введите значение угла, для которого нужно рассчитать тригонометрическую функцию, а потом кликните по соответствующей этой функции кнопке – sin, cos либо tan. Если вас волнуют обратные тригонометрические функции (арксинус, арккосинус либо арктангенс), то вначале кликните кнопку с надписью Inv – она меняет присвоенные руководящим кнопкам калькулятора функции на противоположные.

3. В больше ранних версиях ОС (скажем, Windows XP) для доступа к тригонометрическим функциям нужно раскрыть в меню калькулятора раздел «Вид» и предпочесть строку «Инженерный». Помимо того, взамен кнопки Inv в интерфейсе ветхих версий программы присутствует чекбокс с такой же надписью.

4. Дозволено обойтись и без калькулятора, если у вас есть доступ в интернет. В сети много сервисов, которые предлагают по-различному организованные вычислители тригонометрических функций. Один их особенно комфортных вариантов встроен в поисковую систему Nigma. Перейдя на ее основную страницу, примитивно введите в поле поискового запроса волнующее вас значение – скажем, «арктангенс 30 градусов». Позже нажатия кнопки «Обнаружить!» поисковик рассчитает и покажет итог вычисления – 0,482347907101025.

Видео по теме

Совет 8: Что такое тригонометрические тождества

Тригонометрия – раздел математики для постижения функций, выражающих разные зависимости сторон прямоугольного треугольника от величин острых углов при гипотенузе. Такие функции получили называние тригонометрических, а для облегчения работы с ними были выведены тригонометрические тождества .

Представление тождества в математике обозначает равенство, которое выполняется при всяких значениях доводов входящих в него функций. Тригонометрические тождества – это равенства тригонометрических функций, подтвержденные и принятые для упрощения работы с тригонометрическими формулами.Тригонометрическая функция – это элементарная функция зависимости одного из катетов прямоугольного треугольника от величины острого угла при гипотенузе. Почаще каждого применяются шесть основных тригонометрических функций: sin (синус), cos (косинус), tg (тангенс), ctg (котангенс), sec (секанс) и cosec (косеканс). Эти функции именуются прямыми, существуют также обратные функции, скажем, синус – арксинус, косинус – арккосинус и т.д.Первоначально тригонометрические функции обнаружили отражение в геометрии, после этого распространились в другие области науки: физику, химию, географию, оптику, теорию вероятностей, а также акустику, теорию музыки, фонетику, компьютерную графику и многие другие. Сейчас теснее сложно представить себе математические расчеты без этих функций, правда в дальнем прошлом они использовались только в астрономии и архитектуре.Тригонометрические тождества используются для упрощения работы с длинными тригонометрическими формулами и приведения их к удобоваримому виду. Основных тригонометрических тождеств шесть, они связаны с прямыми тригонометрическими функциями:• tg ? = sin ?/cos ?;• sin^2? + cos^2? = 1;• 1 + tg^2? = 1/cos^2?;• 1 + 1/tg^2? = 1/sin^2?;• sin (?/2 – ?) = cos ?;• cos (?/2 – ?) = sin ?.Эти тождества легко подтвердить из свойств соотношения сторон и углов в прямоугольном треугольнике:sin ? = BC/AC = b/c; cos ? = AB/AC = a/c; tg ? = b/a.Первое тождество tg ? = sin ?/cos ? следует из соотношения сторон в треугольнике и исключением стороны c (гипотенузы) при делении sin на cos. Таким же образом определяется тождество ctg ? = cos ?/sin ?, от того что ctg ? = 1/tg ?.По теореме Пифагора a^2 + b^2 = c^2. Поделим это равенство на c^2, получим второе тождество:a^2/c^2 + b^2/c^2 = 1 => sin^2 ? + cos^2 ? = 1.Третье и четвертое тождества получает путем деления, соответственно, на b^2 и a^2:a^2/b^2 + 1 = c^2/b^2 => tg^2 ? + 1 = 1/cos^2 ?;1 + b^2/a^2 = c^2/a^2 => 1 + 1/tg^2 ? = 1/sin^ ? либо 1 + ctg^2 ? = 1/sin^2 ?.Пятое и шестое основные тождества доказываются через определение суммы острых углов прямоугольного треугольника, которая равна 90° либо ?/2.Больше трудные тригонометрические тождества : формулы сложения доводов, двойного и тройного угла, понижения степени, реформирования суммы либо произведения функций, а также формулы тригонометрической подстановки, а именно выражения основных тригонометрических функций через tg половинного угла:sin ?= (2*tg ?/2)/(1 + tg^2 ?/2);cos ? = (1 – tg^2 ?/2)/(1 = tg^2 ?/2);tg ? = (2*tg ?/2)/(1 – tg^2 ?/2).

Совет 9: Как обнаружить минимальное значение функции

Надобность обнаружить минимальное значение математической функции представляет собой фактический интерес в решении прикладных задач, скажем, в экономике. Огромное значение для предпринимательской деятельности имеет минимизация убытков.

Инструкция

1. Дабы обнаружить минимальное значение функции , необходимо определить, при каком значении довода x0 будет выполняться неравенство y(x0) ? y(x), где x ? x0. Как водится, эта задача решается на определенном промежутке либо во каждой области значений функции , если таковой не задан. Одним из аспектов решения является нахождение неподвижных точек.

2. Стационарной точкой именуется значение довода, при котором производная функции обращается в нуль. Согласно теореме Ферма, если дифференцируемая функция принимает экстремальное значение в некоторой точке (в данном случае – локальный минимум), то эта точка является стационарной.

3. Минимальное значение функция зачастую принимает именно в этой точке, впрочем ее дозволено определить не неизменно. Больше того, не неизменно дозволено с точностью сказать, чему равен минимум функции либо он принимает беспредельно малое значение . Тогда, как водится, находят предел, к которому она тяготится при убывании.

4. Для того дабы определить минимальное значение функции , надобно исполнить последовательность действий, состоящую из четырех этапов: нахождение области определения функции , приобретение неподвижных точек, обзор значений функции в этих точках и на концах промежутка, обнаружение минимума.

5. Выходит, пускай задана некоторая функция y(x) на промежутке с границами в точках А и В. Обнаружьте область ее определения и узнаете, является ли промежуток ее подмножеством.

6. Вычислите производную функции . Приравняйте полученное выражение нулю и обнаружьте корни уравнения. Проверьте, попадают ли эти стационарные точки в промежуток. Если нет, то на дальнейшем этапе они не учитываются.

7. Разглядите промежуток на предмет типа границ: открытые, закрытые, составные либо безмерные. От этого зависит, как вы будете искать минимальное значение . Скажем, отрезок [А, В] является закрытым промежутком. Подставьте их в функцию и рассчитайте значения. То же самое проделайте со стационарной точкой. Выберите наименьший итог.

8. С открытыми и безмерными промежутками дело обстоит несколько труднее. Тут придется искать односторонние пределы, которые не неизменно дают однозначный итог. Скажем, для промежутка с одной закрытой и одной выколотой рубежом [А, В) следует обнаружить функцию при х = А и односторонний предел lim y при х ? В-0.

Источник

как найти период функции
Периодичность функций
Периодичность тригонометрических функций
- - Поделитесь с другими:
Как найти наименьший положительный период функции
- - Инструкция
  - Инструкция
  - Инструкция
  - Инструкция
  - Инструкция
Как найти период тригонометрической функции
- Содержание
- Инструкция

как найти период функции

Как найти период функции вида y=Af(kx+b), где A, k и b — некоторые числа? Поможет формула периода функции

Найти период функции:

1) y=5sin(3x-п/8).

А=2/7, k=-1/11, b=п/5. Поскольку период косинуса T=2п, то

А=0,3, k=5/9, b=п/7. Период тангенса равен п, поэтому период данной функции

А=9, k=0,4, b=-7. Период котангенса равен п, поэтому период данной функции есть

www.uznateshe.ru

Периодичность функций

В этой статье обсуждаем периодичность функций: как определить, периодична ли функция, и каков ее период.

Функция периодична, если некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.

Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.

Периодичная функция

Пример 1: функция имеет период, равный 2: и при . Найдите значение выражения .

Раз наша функция принимает форму части параболы на отрезке [-2; 0] при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – [0;2], и на отрезке [2;4]. Изобразим ее:

Определение значения периодичной функции

Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6 единиц и т.д., тогда . Найдем эти значения функции. В точке (-1) функция принимает значение , в точке (3,5) функция принимает значение .

Теперь найдем значение искомого выражения: .

Строго говоря, функция периодична, если есть такое число Т, что .

Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.

Пример 2. Проверим, периодична ли функция .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется. Значит, функция непериодична.

Пример 3. Проверим, периодична ли функция .

Функцию для удобства представим в виде: .

Установим, выполняется ли условие: , то есть ? Очевидно, что данное условие не выполняется: . Значит, функция непериодична.

Пример 4. Проверим, периодична ли функция . Если функция периодична, то будет выполняться условие: , то есть . Поскольку нам все равно, в какой точке числовой оси мы проведем свое исследование, то очень удобно начать с точки . Тогда , или . Это означает, что либо , либо , то есть либо , либо , а так как главным считается наименьший положительный период, то .

Определение периода функции

В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: .

Пример 5. Определить периодичность функции .

Если Т – период, то .

В это равенство подставим какие-нибудь «удобные» точки, например, . Получим:

Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: . Подставим «удобную» точку :

Пользуясь четностью косинуса и нечетностью синуса можем записать:

Имеем систему:

Уравнения сложим, и получим

, откуда

, при получим – ведь нам нужен наименьший период.

Теперь испробуем второй путь, решим это уравнение: . Из основного тригонометрического тождества:

Оставим в левой части только корень:

Возведем в квадрат:

Тогда либо , либо и .

Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:

и наименьшим будет период при , то есть .

Здесь также необходимо сделать проверку. Подставим полученный период в условие :

, то есть

период данной функции – .

Определение периода функции

Пример 6. Определить периодичность функции и найти ее основной период.

Если Т – период, то

Подставим , имеем

Или , , наименьший период при , .

Проверим:

Определение периода функции

Пример 7. Определим период функции .

Запишем условие периодичности:

, если , то

, откуда , . При , , при , . Проверкой можно показать, что периодом не является. Тогда . Действительно:

Определение периода функции

Пример 8.

Доказать, что периодом функции является .

Тогда:

Пример 9. Доказать, что периодом функции является .

Тогда:

Если , то

, а так как и – одна и та же точка на единичной окружности, то равенство выполняется.

Удачи вам в учебе и надеюсь, эта статья вам помогла.

easy-physic.ru

Периодичность тригонометрических функций

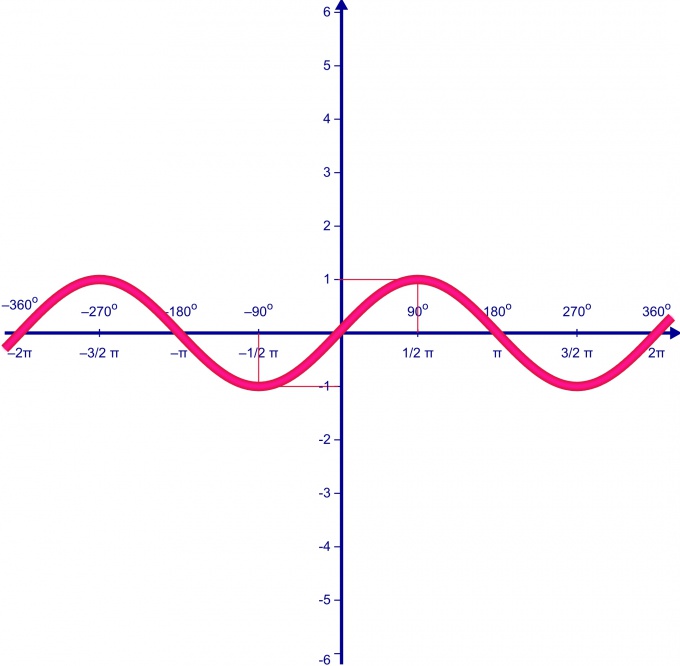
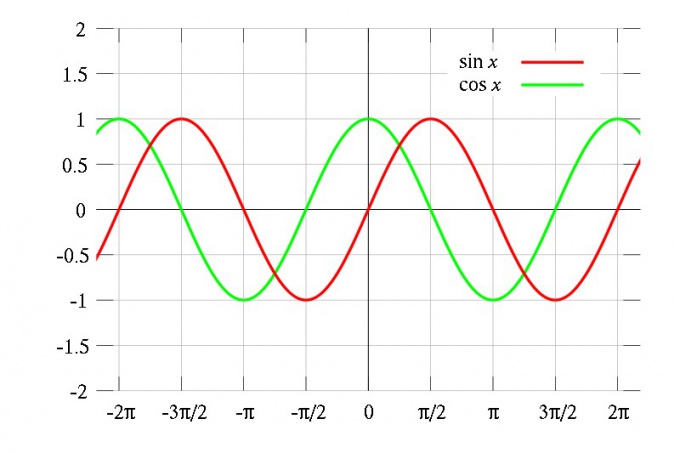
Тригонометрические функции sin(x) и cos(x) являются периодическими, с наименьшим периодом равным 2*π. Тригонометрические функции tg(x) и ctg(x) являются периодическими, с наименьшим периодом равным π.

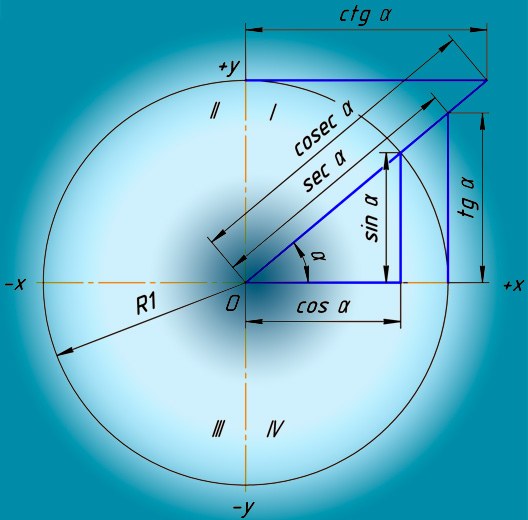
Величины углов (аргументы функций): ( alpha )

Тригонометрические функции:
( sin alpha ),
( cos alpha ),
( tan alpha ),
( cot alpha ),
( sec alpha ),
( csc alpha )

Целые числа: ( n )

Периодической называется функция, которая повторяет свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции): существует такое ненулевое число (T) (период), что на всей области определения функции выполняется равенство ( f(x)=f(x+T) ).

Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими.

( sin x,;cos x ) — периодические функции с наименьшим положительным периодом ( 2pi: )

( sin(x+2kpi)=sin x,;cos(x+2kpi)=cos x,;kinmathbb{Z}. )

( text{tg}x,;text{ctg}x ) — периодические функции с наименьшим положительным периодом ( pi: )

( text{tg}(x+kpi)=text{tg}x,;text{ctg}(x+kpi)=text{ctg}x,;kinmathbb{Z}. )

Тригонометрические функции ( sin alpha ) и ( cos alpha ) являются периодическими, с наименьшим периодом равным ( 2 pi ).

Тригонометрические функции ( tan alpha ) и ( cot alpha ) являются периодическими, с наименьшим периодом равным ( pi ).

Наименьший период функции синус составляет ( 2pi ) или ( 360^circ ):

( sin left( {alpha pm 2pi n} right) = sin alpha )

Наименьший период функции косинус составляет ( 2pi ) или ( 360^circ ):

( cos left( {alpha pm 2pi n} right) = cos alpha )

Наименьший период функции тангенс равен ( pi ) или ( 180^circ ):

( tan left( {alpha pm pi n} right) = tan alpha )

Наименьший период функции котангенс равен ( pi ) или ( 180^circ ):

( cot left( {alpha pm pi n} right) = cot alpha )

Наименьший период функции секанс составляет ( 2pi ) или ( 360^circ ):

( sec left( {alpha pm 2pi n} right) = sec alpha )

Наименьший период функции косеканс составляет ( 2pi ) или ( 360^circ ):

( csc left( {alpha pm 2pi n} right) = csc alpha )

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Как найти наименьший положительный период функции

Минимальный позитивный период функции в тригонометрии обозначается f. Он характеризуется наименьшим значением позитивного числа T, то есть поменьше его значение T теснее не будет являться период ом функции .

Вам понадобится

– математический справочник.

Инструкция

1. Обратите внимание на то, что период ическая функция не неизменно имеет минимальный правильный период . Так, к примеру, в качестве период а непрерывной функции может быть безусловно всякое число, а значит, у нее может и не быть наименьшего позитивного период а. Встречаются также и непостоянные период ические функции , у которых нет наименьшего правильного период а. Впрочем в большинстве случаев минимальный правильный период у период ических функций все же есть.

2. Минимальный период синуса равен 2?. Разглядите подтверждение этого на примере функции y=sin(x). Пускай T будет произвольным период ом синуса, в таком случае sin(a+T)=sin(a) при любом значении a. Если a=?/2, получается, что sin(T+?/2)=sin(?/2)=1. Впрочем sin(x)=1 лишь в том случае, когда x=?/2+2?n, где n представляет собой целое число. Отсель следует, что T=2?n, а значит, наименьшим позитивным значением 2?n является 2?.

3. Минимальный правильный период косинуса тоже равен 2?. Разглядите подтверждение этого на примере функции y=cos(x). Если T будет произвольным период ом косинуса, то cos(a+T)=cos(a). В том случае если a=0, cos(T)=cos(0)=1. Ввиду этого, наименьшим позитивным значением T, при котором cos(x)=1, есть 2?.

4. Рассматривая тот факт, что 2? – период синуса и косинуса, это же значение будет и период ом котангенса, а также тангенса, впрочем не минимальным, от того что, как знаменито, минимальный правильный период тангенса и котангенса равен ?. Удостовериться в этом сумеете, разглядев дальнейший пример: точки, соответствующие числам (х) и (х+?) на тригонометрической окружности, имеют диаметрально противоположное расположение. Расстояние от точки (х) до точки (х+2?) соответствует половине окружности. По определению тангенса и котангенса tg(x+?)=tgx, а ctg(x+?)=ctgx, а значит, минимальный правильный период котангенса и тангенса равен ?.

Вам понадобится

Знания по элементарной математике и началам обзора.

Инструкция

2. Решаем полученное уравнение касательно незнакомой K, так, как словно x – константа. В зависимости от значения К получится несколько вариантов.

Видео по теме

Инструкция

1. Период – это число T, такое что f(x) = f(x+T). Дабы обнаружить период, решают соответствующее уравнение, подставляя в качестве довода x и x+T. При этом пользуются теснее вестимыми периодами для функций. Для функций синуса и косинуса период составляет 2π, а для тангенса и котангенса – π.

Полезный совет
Пользуйтесь формулами для понижения степени функции. Если вам теснее знамениты периоды каких-нибудь функций, пробуйте свести имеющуюся функцию к знаменитым.

Функция, значения которой повторяются через определенное число, именуется периодической . То есть сколько бы периодов вы ни прибавили к значению х, функция будет равна одному и тому же числу. Всякое изыскание периодических функций начинается с поиска наименьшего периода, дабы не исполнять лишнюю работу: довольно исследовать все свойства на отрезке, равном периоду.

Инструкция

1. Воспользуйтесь определением периодической функции . Все значения х в функции замените на (х+Т), где Т – минимальный период функции . Решите полученное уравнение, считая Т незнакомым числом.

2. В итоге вы получите некое тождество, из него испробуйте подобрать наименьший период. Скажем, если получилось равенство sin(2T)=0,5, следственно, 2Т=П/6, то есть Т=П/12.

3. Если равенство получается правильным только при Т=0 либо параметр Т зависит от х (скажем, получилось равенство 2Т=х), делайте итог о том, что функция не периодична.

4. Для того дабы узнать минимальный период функции , содержащей лишь одно тригонометрическое выражение, воспользуйтесь правилом. Если в выражении стоит sin либо cos, периодом для функции будет 2П, а для функций tg, ctg ставьте минимальный период П. Учтите при этом, что функция не должна быть возведена в какую-нибудь степень, а переменная под знаком функции не должна быть умножена на число, хорошее от 1.

5. Если cos либо sin внутри функции построены в четную степень, уменьшите период 2П в два раза. Графически вы можете увидеть это так: график функции , расположенный ниже оси ох, симметрично отразится вверх, следственно функция будет повторяться в два раза почаще.

6. Дабы обнаружить минимальный период функции при том, что угол х умножен на какое либо число, действуете так: определите типовой период этой функции (скажем, для cos это 2П). После этого поделите его на множитель перед переменной. Это и будет желанный минимальный период. Уменьшение периода отменно видно на графике: он сжимается ровно во столько раз, на сколько умножен угол под знаком тригонометрической функции .

7. Обратите внимание, если перед х стоит дробное число поменьше 1, период возрастает, то есть график, наоборот, растягивается.

8. Если в вашем выражении две периодические функции умножены друг на друга, обнаружьте минимальный период для всякой по отдельности. После этого определите минимальный всеобщий множитель для них. Скажем, для периодов П и 2/3П минимальный всеобщий множитель будет 3П (он делится без остатка как на П, так и на 2/3П).

Расчет размера средней заработной платы работников нужен для начисления пособий по временной нетрудоспособности, оплаты командировок. Средний заработок экспертов исчисляется, исходя из реально отработанного времени, и зависит от оклада, надбавок, премий, указанных в штатном расписании.

Вам понадобится

– штатное расписание;
– калькулятор;
– право;
– производственный календарь;
– табель учета рабочего времени либо акт исполненных работ.

Инструкция

1. Для того дабы сделать расчет средней заработной платы работника, вначале определите период, за тот, что нужно ее исчислить. Как водится, таким периодом выступает 12 календарных месяцев. Но если работник трудится на предприятии менее года, к примеру, 10 месяцев, то вам необходимо обнаружить средний заработок за время, которое эксперт исполняет свою трудовую функцию.

2. Сейчас определите сумму заработной платы, которая была реально начислена ему за расчетный период. Для этого используйте расчетные ведомости, по которым работнику выдавались все положенные ему выплаты. Если немыслимо воспользоваться этими документами, то месячный оклад, премии, надбавки умножьте на 12 (либо то число месяцев, которое работник трудится на предприятии, если он оформлен в компании менее года).

3. Рассчитайте среднедневной заработок. Для этого сумму заработной платы за расчетный период поделите на среднее число дней в месяце (в текущее время оно составляет 29,4). Полученный итог поделите на 12.

4. После этого определите число реально отработанного времени. Для этого используйте табель учета рабочего времени. Данный документ должен заполнять табельщик, кадровый служащий либо другой работник, у которого это прописано в должностных обязанностях.

5. Число реально отработанного времени умножьте на среднедневной заработок. Полученная сумма является средней заработной платой эксперта за год. Итог поделите на 12. Это будет среднемесячным заработком. Такой расчет используется для работников, у которых начисление заработной платы зависит от реально отработанного времени.

6. Когда работнику установлена сдельная оплата труда, то тарифную ставку (указанную в штатном расписании и определенную трудовым договором) умножьте на число произведенных изделий (используйте акт исполненных работ либо иной документ, в котором это фиксируется).

Обратите внимание!
Не путайте функции y=cos(x) и y=sin(x) – имея идентичный период, эти функции изображаются по-различному.

Полезный совет
Для большей наглядности изобразите тригонометрическую функцию, у которой рассчитывается минимальный правильный период.

jprosto.ru

Как найти период тригонометрической функции

Содержание

Инструкция

Тригонометрические функции периодичны, то есть повторяются через определенный период. Благодаря этому достаточно исследовать функцию на этом промежутке и распространить найденные свойства на все остальные периоды.

Инструкция

Если вам дано простое выражение, в котором присутствует лишь одна тригонометрическая функция (sin, cos, tg, ctg, sec, cosec), причем угол внутри функции не умножен на какое-либо число, а она сама не возведена в какую-либо степень – воспользуйтесь определением. Для выражений, содержащих sin, cos, sec, cosec смело ставьте период 2П, а если в уравнении есть tg, ctg – то П. Например, для функции у=2 sinх+5 период будет равен 2П.
Если угол х под знаком тригонометрической функции умножен на какое-либо число, то, чтобы найти период данной функции, разделите стандартный период на это число. Например, вам дана функция у= sin 5х. Стандартный период для синуса – 2П, разделив его на 5, вы получите 2П/5 – это и есть искомый период данного выражения.
Чтобы найти период тригонометрической функции, возведенной в степень, оцените четность степени. Для четной степени уменьшите стандартный период в два раза. Например, если вам дана функция у=3 cos^2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите внимание, функции tg, ctg в любой степени периодичны П.
Если вам дано уравнение, содержащее произведение или частное двух тригонометрических функций, сначала найдите период для каждой из них отдельно. Затем найдите минимальное число, которое умещало бы в себе целое количество обоих периодов. Например, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое можно уместить оба этих периода, это 2П, таким образом, искомый период – 2П.
Если вы затрудняетесь действовать предложенным образом или сомневаетесь в ответе, попытайтесь действовать по определению. Возьмите в качестве периода функции Т, он больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. В результате вы найдете значение тригонометрической функции и сможете подобрать минимальный период. Например, в результате упрощения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, равно 2П, это и будет ответ задачи.

completerepair.ru

Источник