Мощность переменного тока
-
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
-
Мощность тока через резистор
-
Мощность тока через конденсатор
-
Мощность тока через катушку
-
Мощность тока на произвольном участке
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и
— мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени
— настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины
и
можно считать постоянными в течение интервала
.
Пусть за время через наш участок прошёл заряд
(в соответствии с правилом выбора знака для силы тока заряд
считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
(1)
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
к оглавлению ▴
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением
. Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
(2)
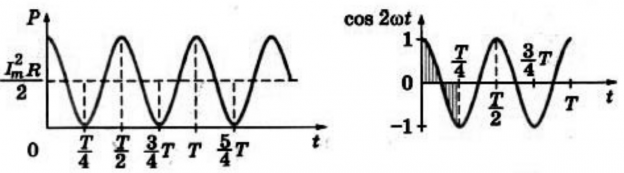
График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.
Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается
колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между
и
. Где же именно?
Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2.
Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
(3)
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
(4)
Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением
, то в обоих случаях лампочка будет гореть одинаково ярко.
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
к оглавлению ▴
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на
:
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3.
Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.
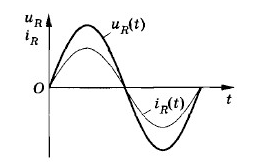
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).
Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
к оглавлению ▴
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на
:
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).
Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
к оглавлению ▴
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
(5)
Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:
В результате получим:
(6)
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
(7)
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки
, и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
Тогда,
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
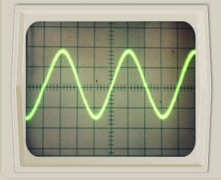
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
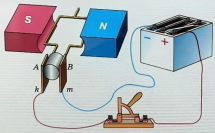
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
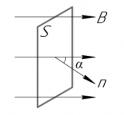
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
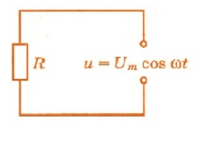
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
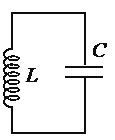
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
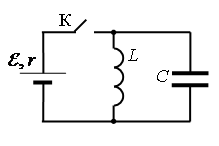
Задание EF18735
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
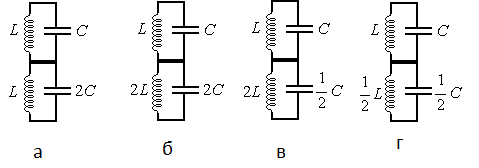
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
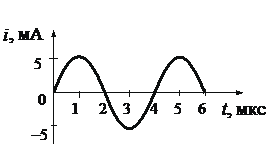
Задание EF18656
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.6k
Переменный электроток способен изменяться по направлению или своей величине внутри электрической цепи. Мощность переменного тока представляет собой произведение тока и напряжения.
Мощность в цепи переменного тока
Внутри схемы переменного электротока различается три вида мощностей: активного типа или Р, реактивного типа или Q, и полного типа или S. В первом случае стандартной единицей замеров является Ватт (Вт или W), при этом формула для вычисления активных мощностных параметров:
P = U × I × cos φ.
От характеристик коэффициента угла фазового сдвига или последнего показателя напрямую зависят расчеты положительной или отрицательной активной мощности.
Для замеров мощности реактивного типа применяется специальный вольт-ампер с обозначением «Вар» или Var.
Данной величиной характеризуются нагрузки, которые формируются внутри конструкций электротехнического типа под воздействием колебаний электромагнитных полей в цепях переменного синусоидального тока.
Расчет осуществляется на базе среднеквадратичных показателей напряжения и токовых параметров, умноженных на угловую синусоиду фазного сдвига, согласно значениям:
Q = U × I × sin φ.
В условиях значений на уровне 0/+90° синусовая величина будет положительной, а для показателей в пределах 0/-90° — только отрицательной. Замеры полной электромощности осуществляются исключительно в вольт-амперах (В·А или V·A).
Зависимость мощности от времени для переменного и постоянного тока
Величину, соответствующую произведению стандартного напряжения в зажимной области с показателями электротока периодического типа внутри цепи, целесообразно рассчитывать в соответствии с формулами:
S = U × I или S = √Р2 + Q2, где
- значение Р представлено активной мощностью;
- значение Q2 — показатель реактивной мощности.
Немаловажное значение отводится комплексной мощности, соответствующей импедансу. В любом случае необходимо учитывать, что положительная мощность соответствует P > 0, а отрицательные показатели — P < 0.
Крупными отечественными производителями электрической энергии генерируется переменный ток с так называемой промышленной частотой, равной 50 Гц, и показателями напряжения в пределах 10-20 кВ, а электрическое напряжение повышается на специальных трансформаторных подстанциях.
Формула мощности переменного тока

Несмотря на сложность измерения мощности, важно помнить, что такие данные не показательны, поэтому с практической точки зрения интерес представляет активная средняя мощность в определенном периоде.
В однофазной цепи
Для однофазной цепи используется формула определения полной мощности: S = U × I, где
- S — показатели полных мощностных характеристик (Ва);
- I — уровень действующей силы электротока с учетом обмотки генератора (А);
- U — параметры расчетного действующего значения напряжения в генераторе (В).
Полные мощностные характеристики, учитываемые при стандартных самостоятельных расчетах, влияют на габариты генератора с переменными показателями электрического тока, что обусловлено поперечным сечением и числом витков обмоточных проводов, а также толщиной изоляционного материала. Для активного и реактивного сопротивления важна мощность, расходуемая при активном сопротивлении, и в реактивной части.
Однофазные электрические цепи переменного тока
Реактивные мощностные показатели обуславливаются энергетическими колебаниями в условиях формирования и потери электрических или магнитных полей. Запасаемая внутри поля такого сопротивления электроэнергия поступательно возвращается обратно на генератор, который подключается к стандартной электрической цепи.
Наличие реактивных токов между реактивным приемником и генератором, которые имеют индуктивное и емкостное сопротивление, способствует бесполезной загрузке линии и генератора, что сопровождается дополнительными энергетическими потерями.
В трехфазной цепи
Мощностные показатели переменного тока при равномерной трехфазной нагрузке определяются наличием равноценного тока, протекающего по проводникам фазы. В этом случае показатели силы тока в условиях использования нулевого проводника составляют «О». Формула для расчета мощности переменного тока в условиях трехфазной сети: Р = 3 × U φ × I × соs(φ).
Симметричная (равномерная) нагрузка фаз в трехпроводной цепи трехфазного тока
Протекание внутри фазных проводников различных по величине токов представляет собой несимметричную, или неравномерную нагрузку. При этом именно несимметричная нагрузка сопровождается протеканием тока по нулевым или нейтральным проводам, поэтому уровень мощностных показателей определяется в соответствии со стандартной и общеизвестной формулой:
Робщая = Uа × Iа × соs(φ1) + Ub × Ib × соs(φ2) + Uс × Iс × соs(φ3).
Средняя мощность в активной нагрузке
Мощностные параметры электросети или любой установки являются наиболее важными данными практически любого электрического прибора. Передача проходящих или потребляемых мощностных характеристик активного типа осуществляются в течение определенного периода времени.
Табличные значения средних мощностных характеристик основных бытовых приборов
| Устройство | Показатели |
| Зарядное устройство | 2,0 Вт/час |
| Люминесцентные лампы «ДРЛ» | 50 Вт/час и более |
| Электрический чайник | 1,5 кВт/час |
| Акустические системы | 30 Вт/час |
| Стиральная машина | 2,5 кВт/час |
| Мойка под высоким давлением | 3,5 кВт/час |
| Инверторы полуавтоматического типа | 3,5 кВт/час |
| Кухонный блендер | 1,0-1,2 кВт/час |
| Микроволновая СВЧ-печь | 1,8 кВт/час |
| Кухонные тостеры | 1,2 кВт/час |
| Телевизор | 0,2 кВт |
| Холодильник | 0,4 кВт |
| Пылесос | 1,0 кВт |
| Компьютер стационарный | 0,55 кВт |
| Электрическая плита | 2,5 кВт/час |
| Фен для сушки волос | 1,0 кВт/час |
| Утюг | 1,0 кВт/час |
| Электрическая духовка | 1,2 кВт/час |
| Электрический обогреватель | 1,4 кВт/час |
Мощность при наличии сдвига фаз между током и напряжением
В условиях переменного электротока совпадения в токовом направлении и напряжении отмечаются только при отсутствии катушечной индукции и конденсаторов. В этом случае векторное направление тока и напряжения идентичны. Присутствие в схеме катушек и конденсатора сопровождается совпадением токовых фаз и показателей напряжения, но векторное вращение происходит на одинаковой скорости и при неизменных параметрах угла.
Фазовое смещение или сдвиг совпадает с углом, который наблюдается между векторными радиусами токовых показателей и параметров напряжения, а отставание в этих критериях провоцирует несовпадение.
Сдвиг фаз переменного тока и напряжения
При этом мощностные характеристики являются отрицательными за счет произведения положительной и отрицательной величин. В подобных условиях электрическая цепь внешнего типа становится стандартным источником электроэнергии. Незначительный объем энергии, поступающей в цепь на положительных показателях мощности, осуществляет возврат только при наличии отрицательных значений.
Продолжительность частей периода напрямую зависит от уровня фазового сдвига, при этом показатели смещения определяются длительностью отрицательных мощностей, или так называемыми средними мощностными характеристиками электрического тока.
Баланс мощностей
Самостоятельное нахождение некоторых электротехнических неизвестных, как правило, требует обязательной проверки правильности полученных значений с учетом баланса мощностей.
В соответствии с общепринятыми характеристиками, баланс в электрической цепи базируется на законе сохранения энергии, поэтому суммарные потребляемые и отдаваемые мощности должны быть равными.
При расчетах учитываются показатели эквивалентного сопротивления и знакомый большинству из курса физики закон Ома.
Допускаются небольшие расхождения в значениях, что обуславливается стандартными округлениями, осуществляемыми в процессе выполнения самостоятельных расчетов. Таким образом, вне зависимости от уровня сложности создаваемой цепи баланс обязательно должен сходиться, что является гарантией сохранения работоспособности и полной безопасности эксплуатации.
Величина l
/dkэ
= Т , обратная величине показателя
экспоненциала в решении элементарного
уравнения кинетики реактора n(t) = no
exp (dkэ
t / l), называется периодом реактора при
заданной величине реактивности.
Подобное название
обусловлено тем, что, во-первых, эта
величина имеет размерность времени, а,
во-вторых, само это название заимствовано
из математики, где период экспоненциальной
функции является наиболее наглядной
её характеристикой. Смысл этой величины
применительно к рассматриваемому случаю
можно пояснить следующим образом.
Решение элементарного уравнения кинетики
реактора с учётом принятого обозначения
периода имеет вид:
n(t)
/ no
= exp ( t / T ) , (11.17)
из которого следует,
что за время t = T величина плотности
нейтронов в реакторе изменяется в е =
2.718281… раз ( при определённой постоянной
величине сообщённой реактору реактивности,
или, что то же, при постоянной величине
избыточного коэффициента размножения
dkэ
).
При положительной
величине реактивности (r
>
0) величина периода реактора также имеет
положительный
знак, при
отрицательной величине реактивности
(r
<
0) величина периода реактора отрицательна.
Период реактора
является единственной характеристикой
для чисто экспоненциального переходного
процесса n(t) в реакторе, позволяющей
оценивать интенсивность изменения
плотности нейтронов или мощности
реактора, и при этом является легко
воспринимаемой и легко
измеряемой
величиной. Чем выше величина периода
Т, тем менее круто (более плавно) происходит
изменение мощности при сообщении
критическому реактору реактивности
того или иного знака.
Из определения
периода следует, что его величина
определяется величиной сообщённой
реактору реактивности ( или величиной
dkэ
). Из этого следует, что при относительно
малых значениях реактивности величина
периода обратно пропорциональна величине
реактивности, причём коэффициентом
пропорциональности
Т
»l /r(11.18)
служит величина
среднего времени жизни поколения
нейтронов в реакторе l.
Рис. 11.4. Изображения переходных процессов,
вытекающих из решения элементарного
уравнения кинетики реактора, в натуральной
и полулогарифмической системах координат.
Из правого графика следует, что величина,
обратная периоду реактора, интерпретируется
как тангенс угла наклона к оси абсцисс
прямой переходного процесса в
полулогарифмической системе координат.
В переходных
процессах n(t), которые в соответствии с
решением элементарного уравнения
кинетики имеют чисто экспоненциальный
вид, величина Т при постоянной величине
сообщённой критическому реактору
реактивности — есть величина постоянная
в течение всего времени переходного
процесса n(t), а это говорит о том, что и
величина среднего времени жизни
поколения нейтронов (l) — тоже предполагается
величиной постоянной в любой момент
времени переходного процесса.
Если построить
любую из экспонент, даваемых решением
ЭУКР, в полулогарифмической системе
координат ln n(t) = f(t), то экспоненциальный
процесс в такой системе координат
изобразится прямыми линиями с угловыми
коэффициентами, равными величине
обратного периода (1 / T) при любом знаке
реактивности. Пара таких экспонент
(возрастающая — при r
>
0 и убывающая — при r
<
0) показаны на рис.11.5.
Рис.11.5. Экспоненциальные переходные
процессы n(t) в натуральной и
полулогарифмической системах координат
(линии 1 соответствуют положительной,
линии 2 — нулевой, линии 3 — отрицательной
реактивности).
Угловой коэффициент
прямой линии (если вспоминать аналитическую
геометрию) — это тангенс угла наклона
её к оси абсцисс. В более общем случае,
применительно к кривым линиям, тангенс
угла наклона касательной в точке кривой
линии — интерпретируется как значение
первой производной функции, описывающей
эту линию, в этой точке.
Поэтому, если
прологарифмировать по точкам график
переходного процесса в реальном реакторе
(о котором говорилось в п.11.1.1), становится
ясным, что величина периода реактора
будет примерно
постоянной только в развитой части
переходного процесса, а на стадии
начального скачка величина периода
реактора — переменна.
Рис.11.6. Переходные процессы в реальном
реакторе при сообщении ему положительной
( 1), нулевой (2) или отрицательной (3)
реактивности постоянной величины,
построенные в полулогарифмической
системе координат. Наклон линий на
стадии начального скачка, как видите,
является величиной переменной.
Приходится признать,
что на первой стадии переходного процесса
n(t), то есть на стадии начального скачка,
при постоянной величине реактивности
(или dkэ)
переменной величиной является величина
среднего времени жизни поколения
нейтронов. За счёт чего? —
Очевидно, за счёт того, что в течение
начального скачка переменной величиной
является соотношение скоростей генерации
мгновенных и запаздывающих нейтронов.
Величина периода
реактора Т, являясь удобной аналитической
характеристикой интенсивности переходного
процесса n(t) в реакторе, для
практика-оператора реакторной установки
не очень удобна с точки зрения её
практического измерения. Представим
себе, как это делается: в определённый
момент переходного процесса, когда
стрелка измерителя нейтронной мощности
проходит определённое деление на его
шкале, включается секундомер, который
должен быть остановлен в тот момент,
когда стрелка прибора будет показывать
значение нейтронной мощности, в
2.71828…раза превосходящее значение при
включении секундомера; в этом случае
секундомер как раз и покажет величину
периода реактора Т. Оператору для
измерения величины периода необходимо
знать, на каком делении следует остановить
секундомер, для чего он должен выполнить
быстрое вычисление: величину начальной
нейтронной мощности умножить на число
е = 2.7182818.., что, конечно, можно проделать
при наличии калькулятора, но “в уме”
такое вычисление явно затруднительно.
Поэтому операторы
пользуются более практичной характеристикой,
пропорциональной величине периода
реактора Т и называемой периодом
удвоения мощности
реактора ( Т2),
которая, как следует из её названия,
представляет собой время
изменения нейтронной мощности реактора
в два раза.
Взаимосвязь величин Т2
и Т (при одной и той же величине сообщаемой
реактору реактивности r)
вытекает из того же решения ЭУКР. Если
в него подставить значение t = T2
, то отношение n(T2)
/ no
= 2 (как следует из определения ), и,
следовательно
2 = exp ( T2
/ T ), или Т2
/ T = ln 2 »
0.693, откуда следует, что
Т2
»
0.693 Т, или, наоборот, Т »
1.44 Т2
(11.19)
И последнее.
Элементарное уравнение кинетики реактора
и его решение, несмотря на простоту,
неплохо служит в прикладном плане, давая
возможность непосредственно измерять
мгновенное значение периода реактора
или периода удвоения его мощности, а,
точнее, указывает путь к реализации
периодомера — прибора для измерения
величины периода. Если в выражение
элементарного уравнения кинетики
подставить величину периода реактора
Т = l / dkэ,
то получается
dn /dt = n / T,
откуда следует, что Т = (dn / dt) / n(t),
(11.20)
то
есть:
Мгновенное
значение величины периода реактора
есть отношение производной изменения
плотности нейтронов в реакторе к
мгновенному значению самой величины
плотности нейтронов.
Нейтронная
мощность реактора измеряется, как
известно, с помощью нейтронных камер,
по величине электрического тока камер,
пропорциональной величине измеряемой
нейтронной мощности реактора. Из
последней формулы для Т вытекает, что
для измерения мгновенного значения
величины периода реактора Т(t) следует
выходной сигнал ионизационных камер:
-
продифференцировать
(в дифференцирующем блоке); -
получить его
обратную величину (в конвертирующем
блоке); -
подать выходные
сигналы с этих двух блоков на блок
перемножения, в котором получается
сигнал, пропорциональный их произведению
(и пропорциональный величине периода
реактора Т); -
пропустить этот
сигнал через масштабирующий блок с
коэффициентом 0.693 для получения
электрического сигнала, пропорционального
величине периода удвоения мощности
реактора Т2
и подать полученный сигнал на показывающий
электроизмерительный прибор.
Рис. 11.6. Принципиальная блок-схема
измерителя периода удвоения мощности
реактора.
Краткие
выводы
Кинетика реактора
— раздел теории, изучающий и описывающий
закономерности изменения во времени
плотности нейтронов в реакторе при
ненулевых реактивностях.
В кинетическом
описании переходных процессов существенную
роль играет величина времени
жизни поколения нейтронов в реакторе.
Элементарное
уравнение кинетики реактора
, которое не учитывает различий между
мгновенными и запаздывающими нейтронами,
не даёт полного объяснения закономерного
характера переходных процессов n(t) в
реальных реакторах при сообщении им
реактивности. Его решение объясняет
лишь экспоненциальную стадию в развитой
части переходных процессов, но не даёт
объяснения наличию в реальных переходных
процессах стадии начального скачка
плотности нейтронов, с которой начинается
переходный процесс n(t). Это вынуждает
заниматься более детальным изучением
закономерностей генерации нейтронов
в реакторе и выделять среди них
запаздывающие нейтроны.
Запаздывающие
нейтроны
получаются за счёт выхода при делении
ядер топлива тринадцати основных типов
потенциально нейтроноактивных осколков
деления, называемых предшественниками
запаздывающих нейтронов. Предшественники,
испытывая первым b-распад,
в качестве дочерних продуктов этого
распада дают нейтроноактивные излучатели
запаздывающих нейтронов, из которых и
испускаются запаздывающие нейтроны.
Отличия
запаздывающих нейтронов,
испускаемых различными излучателями,
заключаются в различных величинах их
начальной кинетической энергии и их
абсолютными долями выхода, а также
величинами времени запаздывания. Для
более компактного описания тринадцать
типов запаздывающих нейтронов объединены
в шесть групп по принципу близости их
основных характеристик. Эти шесть групп
характеризуются усреднёнными значениями
долей выхода, постоянных b-
распада и начальной энергии. Средняя
начальная кинетическая энергия
запаздывающих нейтронов всех шести
групп равна 0.49 МэВ, а суммарная доля
выхода в общем балансе генерации
нейтронов для запаздывающих нейтронов
в критическом реакторе бесконечных
размеров равна 0.0064 (для 235U)
и 0.0021 (для 239Pu).
В реальном уран-плутониевом топливе
энергетических реакторов усреднённая
величина доли выхода запаздывающих
нейтронов в процессе кампании активной
зоны снижается пропорционально уменьшению
содержания 235U
в топливе. В реакторах АЭС величина
эффективной доли выхода запаздывающих
нейтронов уменьшается от 0.0064 (для
свежего топлива в начале кампании) до
0.0045 — 0.0050 (в конце кампании). В реакторах
больших размеров (реакторах АЭС) величины
теоретической и эффективной долей
выхода запаздывающих нейтронов
приблизительно равны (величина ценности
запаздывающих нейтронов в этих реакторах
близка к единице).
Роль запаздывающих
нейтронов
состоит в том, что относительно небольшое
их количество в реакторе увеличивает
значение среднего времени жизни
поколения нейтронов как минимум на три
порядка величины (от ~10
-4
до ~
10 -1
с), благодаря чему и реализуется
возможность безопасного управления
реактором.
Характеристиками
интенсивности развития экспоненциальных
переходных процессов n(t)
в реакторах являются период реактора
и период удвоения мощности. Последняя
характеристика для практика более
удобна из-за простоты её “безоружного”
измерения. Эти две характеристики
пропорционально взаимосвязаны друг с
другом зависимостью:
T2
»
0.693 Т , или Т »
1.44 Т2
Математической
интерпретацией мгновенного значения
изменяющегося периода Т является
отношение мгновенных значений производной
плотности нейтронов и самой величины
плотности нейтронов в реакторе.
-
Кинетика реактора
с учётом запаздывающих нейтронов
Здесь, как и в
предыдущей теме, будет рассматриваться
кинетика «холодного» реактора в
точечно-параметрическом приближении.
Как и ранее, оговариваемся, что в рамках
нашего рассмотрения величина положительной
или отрицательной реактивности
первоначально критическому реактору
сообщается самым простым и жёстким
образом — мгновенным скачком (рис.12.1).
Рис.12.1. Мгновенный скачок
положительной и отрицательной
реактивности.
Дело в том, что для
изучения общих закономерностей поведения
плотности нейтронов n(t) надо, чтобы
величина вводимой реактивности во
времени изменялась одинаковым образом,
общим для всех случаев сообщения реактору
конкретной величины реактивности,
независимо от её величины и знака.
Поэтому и способ сообщения реактору
реактивности избран общим: мгновенный
скачок.
В действительности
реальному реактору таким образом
сообщить заданную величину реактивности
невозможно: при ограниченной скорости
перемещения органа СУЗ перемещение
поглотителя всегда требует определённого
конечного времени, тем более короткого,
чем выше скорость линейного перемещения
стержня-поглотителя. Но вследствие
инерционности воплощённой в металле
кинематической схемы любого органа СУЗ
процесс сообщения реактивности
критическому реактору всегда будет
иметь более “мягкий” (растянутый во
времени) характер: на начальном участке
перемещения поглотителя требуется
преодолеть инерцию покоя всего механизма,
на конечном участке — наоборот — инерцию
движения, а на стадии равномерного
перемещения поглотителя (с постоянной
скоростью) процесс сообщения реактору
реактивности имеет приблизительно
линейный характер (рис.12.2).
Рис.12.2. Характер реального процесса
сообщения реактору положительной и
отрицательной реактивности во времени
за счёт перемещения подвижного
стержня-поглотителя в реакторе из
критического положения.
Рассмотрение
случая сообщения реактивности реактору
мгновенным скачком обусловлено ещё и
тем, что любые иные реальные способы
воздействия на реактор более
безопасны.
-
Система
дифференциальных уравнений кинетики
реактора с учётом
шести
групп запаздывающих нейтронов.
Очевидно, что
плотность тепловых нейтронов, полученных
в результате замедления в любом
микрообъёме активной зоны в любой момент
времени всегда равна сумме плотностей
тепловых нейтронов, полученных в
результате замедления мгновенных и
запаздывающих нейтронов.
n(t)
= nм(t)
+ nз(t).
Из этой очевидности
вытекает и другая: так как производная
суммы двух функций одного аргумента
равна сумме их производных, то
dn
/dn = dnм
/dt + dnз
/dt . (12.1)
На основе этого
равенства и построен вывод первого из
системы дифференциальных уравнений
кинетики реактора — уравнения скорости
изменения плотности нейтронов в реакторе.
Примечание.Впредь, говоря о плотности
тепловых нейтронов, получаемых в
результате замедления мгновенных (или
запаздывающих) нейтронов, будем выражаться
кратко: “плотность мгновенных
(запаздывающих) нейтронов”, оговаривая
лишь случаи, когда использование таких
кратких выражений приводит к двусмысленному
пониманию их.
-
Дифференциальное
уравнение скорости изменения плотности
нейтронов.
Используя один из простейших приёмов
математической физики, величину
эффективного коэффициента размножения
нейтронов в реакторе можно представить
как сумму двух слагаемых, каждое из
которых словно бы отдельно ответственно
за размножение мгновенных и запаздывающих
нейтронов:
kэ
= kэ
— kэ
bэ
+ kэbэ
= kэ
(1 — bэ)
+ kэbэ
= kэм
+ kэз
, (12.2)
где kэм
= kэ
( 1 — bэ
) — произведение эффективного коэффициента
размножения на долю выхода мгновенных
нейтронов, называемое коэффициентом
размножения на мгновенных нейтронах,
а
kэз
= kэ
bэ
— произведение
эффективного коэффициента размножения
на эффективную долю выхода запаздывающих
нейтронов, называемое коэффициентом
размножения на запаздывающих нейтронах.
Величина bэ
— в обоих случаях — это суммарная
эффективная доля выхода запаздывающих
нейтронов всех групп (мы рассматриваем
приближение с шестью группами запаздывающих
нейтронов).
Аналогично понятию
избыточного коэффициента размножения
(dkэ
= kэ
-1) вводится понятие избыточного
коэффициента размножения на мгновенных
нейтронах, величина которого будет
равна:
dkэм
= kэм
— 1 = kэ
(1 — bэ)
— 1 = kэ
— 1 — kэbэ
= dkэ
— kэbэ
»
r
— bэ
, (12.3)
так как при kэ»1 величинаdkэ»r, а kэbэ»bэ
.
Обособленное
рассмотрение размножения на мгновенных
нейтронах даёт возможность первое
слагаемое правой части (12.1) записать
сразу, без вывода, используя известное
нам элементарное уравнение кинетики
реактора, в котором следует произвести
лишь формальную замену: вместо dkэ
— подставить величинуdkэм»r-bэ, а вместо среднего времени жизни
поколения нейтронов — подставить l —
время жизни мгновенных нейтронов, то
есть
dnм/dt
= [(r
— bэ)
/ l] n(t) (12.4)
Примечание.
Из (12.3), строго говоря, следует, что
dkэм
= dkэ
— kэbэ
= kэ
[(dkэ
/ kэ)
— bэ]
= kэ
(r
— bэ)
,
но, как уже неоднократно отмечалось,
величина kэв практике управления
реальными энергетическими реакторами
мало когда отличается от единицы более
чем на 0.002, поэтому величина kэбез
заметного ущерба для точности может
быть принята равной единице
.
Второе слагаемое
в правой части (12.1.1) — скорость изменения
плотности тепловых нейтронов, полученных
в результате замедления запаздывающих
нейтронов dnз
/dt. Эта величина находится из простых
рассуждений.
Предположим, что
реальная концентрация ядер-предшественников
запаздывающих нейтронов i-ой группы в
рассматриваемый момент времени равна
Сi.
Это означает, что в единичном объёме
активной зоны будет происходить b-распад
этих предшественников со скоростью
liCi
( где li
— постоянная b-распада
предшественников i-ой группы. Это, в свою
очередь, означает, что в этом единичном
объёме ежесекундно будут образовываться
liCi
ядер-излучателей запаздывающих нейтронов
этой группы, а, поскольку каждое
ядро-излучатель практически без
запаздывания испускает один запаздывающий
нейтрон, величина liCi
является ещё и мгновенным значением
скорости образования быстрых запаздывающих
нейтронов i-ой группы.
Если бы эти быстрые
запаздывающие нейтроны со стопроцентной
достоверностью избегали утечки и
резонансного захвата при замедлении,
то в каждом единичном объёме активной
зоны в среднем из них рождалось бы
столько же
тепловых нейтронов за 1 с, но если учесть,
что из всех их только (рз
j)-ая
часть остаётся в активной зоне, то
фактически в каждом единичном объёме
активной зоны ежесекундно будет рождаться
liCi
pз
j
тепловых нейтронов, получаемых из
запаздывающих нейтронов i-ой группы.
Общая же скорость генерации тепловых
нейтронов из запаздывающих нейтронов
всех шести групп будет равна
6
6
dnз
/ dt = S
liCi
pз
j
= S
li
ci
, (12.5)
i=1
i=1
где обозначенная
малым символом (сi)
величина ci
= Ci
pзj
, (12.6)
называется
эффективной
концентрацией предшественников i-ой
группы. Эта
величина, введенная в обиход из соображений
чистого удобства (компактности записи),
имеет смысл некоторой условной
эквивалентной концентрации тех же
предшественников, из которых ежесекундно
получалось бы реальное количество
тепловых запаздывающих нейтронов i-ой
группы в случае, когда утечка и резонансный
захват замедляющихся нейтронов в
реакторе отсутствовали бы.
Таким образом, с
учётом выражений (12.5) и (12.4) исходное
уравнение для скорости изменения
плотности нейтронов в реакторе (12.1)
приобретает вид:
6
dn /
dt = [(r
— bэ)
/ l ] n(t) + S
li
ci(t)
(12.7)
i=1
Это уравнение
является неопределённым,
так как, кроме основной неизвестной
функции n(t) оно содержит ещё шесть
неизвестных функций — временных
зависимостей эффективных концентраций
предшественников запаздывающих нейтронов
всех шести групп. Поэтому для того, чтобы
получить конкретное
решение, необходимо замкнуть систему,
то есть присоединить к (12.7) ещё, как
минимум, шесть дифференциальных
уравнений, в которых функции сi(t)
фигурировали бы независимым от уравнения
(12.7) образом.
12.1.2.Дифференциальные
уравнения скоростей изменения эффективных
концентраций предшественников
запаздывающих нейтронов шести групп.
Логический вид этих шести уравнений
одинаков:
dCi/dt
= (скорость генерации предшественников
i-ой группы) — (скорость их b-распада)
(12.8)
Первое слагаемое
правой части (12.8) получается из следующих
рассуждений. Если n(t)
— средняя по объёму активной зоны
плотность тепловых нейтронов в некоторый
произвольный момент времени (t),
то через промежуток времени, равный
среднему времени жизни поколения
мгновенных нейтронов ( l ) плотность
нейтронов станет равной kэn
(что следует из определения эффективного
коэффициента размножения kэ).
Эти тепловые нейтроны очередного
поколения получены в результате
замедления быстрых нейтронов, исходное
число которых в единичном объёме активной
зоны было kэ
n /pз
j
, то есть рождались эти нейтроны со
средней скоростью kэn
/ pзj
l в каждом см3
активной зоны за 1 с. Но среди всех этих
быстрых нейтронов bi-ая
часть рождались как запаздывающие
нейтроны i-ой группы, а так как каждый
запаздывающий нейтрон i-ой группы
испускался одним излучателем, а каждый
излучатель получался в результате
b-распада
одного предшественника i-ой группы, то
из этого следует, что скорость генерации
предшественников i-ой группы составляет
kэn
bэi
/ pзj
l ядер/см3
с. Такова
величина первого слагаемого правой
части логического уравнения (12.8).
Со вторым слагаемым
этого уравнения дело значительно проще:
в соответствии с известным законом
радиоактивного распада скорость
b-распада
предшественников i-ой группы определяется
только наличной в данный момент времени
концентрацией их Сi,
то есть равна liCi.
Поэтому искомое
дифференциальное уравнение для скорости
изменения действительной концентрации
предшественников i-ой группы будет :
dCi
/ dt = (kэ
bэi
/ pзj
l) n(t) — li
Ci(t)
,
а если, руководствуясь
формулой (12.6), перейти к эффективным
концентрациям предшественников любой
группы, и полагая, что, как и в предыдущем
выводе, kэ
»
1, то:
dci
/ dt = ( bэi/
l) n(t) — li
ci(t)
(12.9)
Таков общий вид
шести дифференциальных уравнений для
скоростей изменения эффективных
концентраций предшественников
запаздывающих нейтронов шести групп.
Таким образом
полная замкнутая система семи
дифференциальных уравнений кинетики
реактора с учётом запаздывающих нейтронов
имеет вид:
6
dn / dt =
[(r
— bэ)
/ l ] n(t) + S
lici(t)
(12.10)
i=1
dci
/ dt = (bэi
/ l) n(t) — li
ci(t)
i = 1, 2,…, 6 (12.11)
-
Решение системы
дифференциальных уравнений кинетики.
Одинаковый вид всех дифференциальных
уравнений кинетики подсказывает, что
их решения можно отыскать в форме
выражений:
n(t)
= no
exp (t / T) (12.12) и
ci(t)
= cio
exp (t / T) , (12.13)
где no
и cio
— соответственно величины плотности
нейтронов и эффективной концентрации
предшественников запаздывающих нейтронов
i-ой группы в момент времени t = 0, когда
реактор перед сообщением ему реактивности
был ещё критичен.
Но, коль скоро эти
выражения являются решениями системы
уравнений кинетики, то подстановка их
самих и их производных:
dn / dt = [no
exp (t / T)] / T = n(t) / T
(12.14)
dci
/ dt = [cioexp
(t / T)] / T = ci(t)
/ T (12.15)
в исходную систему
уравнений должна обратить последние в
тождества.
В этих выражениях
параметр Т имеет физический смысл
периода соответствующих экспоненциальных
процессов.
Примечание. Впредь ради краткости
записи функции n(t) и ci(t) будем
обозначать просто n и ci.
Подставим вначале
(12.15) только в левую часть уравнения
(12.11):
сi
/ T = (bэi
/ l) n — li
ci,
откуда ci
= bэi
T n / (1 + liT)
l . (12.16)
Далее выражения
(12.16) и (12.14) подставляются в уравнение
(12.10):
6
n / T = [(r
— bэ)
/ l ] n + S
{libэiT
/ (1 + liT)
l} n
i=1
Умножив обе части
полученного равенства на (l / n), получаем:
6
l /
T = r
— bэ
+ S
{libэiT
/(1 + liT)}
(12.17)
i=1
6
Если учесть,
что bэ
= S
bэi
, то, объединив две суммы в правой части
(12.17) в одну
i=1
и приведя выражение
под знаком суммы к общему знаменателю,
несложно получить:
6
r
= (l / T) + S
bэi
/ (1 + liT)
(12.18)
i=1
Уравнение (12.18) по
отношению к уравнению (12.10) является
характеристическим
и называется уравнением
обратных часов.
Замечание. Получена, строго
говоря, приближённая форма уравнения
обратных часов, поскольку в процессе
его вывода было принято одно допущение:
предполагалось, что величина эффективного
коэффициента размножения kэочень
мало отличается от единицы, в связи с
чем допускалось, чтоr»dkэ.
Эта натяжка незначительно влияет на
точность решения и не меняет качественного
характера решения системы дифференциальных
уравнений кинетики реактора, но даёт
возможность при этом значительно
сократить объём математических
преобразований при выводе уравнения
обратных часов. Если бы мы не прибегали
к указанному допущению, в результате
более громоздкого вывода можно было бы
получить более точное выражение
для уравнения обратных часов
(сравните):
6
r
= l /(T + l) + [T /(T + l)] S
bэi
/ (1 + li
T) (12.18а)
i=1
Уравнение обратных
часов настолько важно и для анализа
решений системы дифференциальных
уравнений кинетики реактора, и для
практической деятельности оператора
реакторной установки, что мы временно
прервём ход решения дифференциальных
уравнений кинетики и остановимся на
нём более подробно.
-
Уравнение
обратных часов.
а ) Уравнение
обратных часов как характеристическое
уравнение системы дифференциальных
уравнений кинетики реактора.
Развёрнутый вид уравнения обратных
часов:
r
= (l/T) + bэ1/(1+l1T)
+ bэ2/(1+l2T)
+ bэ3/(1+l3T)
+ bэ4/(1+l4T)+
bэ5/(1+l5Т)
+ bэ6/
(1 + l6T)
свидетельствует
о том, что это — алгебраическое уравнение
седьмой степени относительно Т. Для
того, чтобы понять это, достаточно
мысленно представить, что получится в
числителе выражения правой части
уравнения после приведения его к общему
знаменателю: седьмая степень уравнения
становится очевидной. А это значит, что
уравнение обратных часов в самом общем
случае должно иметь семь корней.
В разделе математики
“Решение дифференциальных уравнений”
говорится, что вид, величины и знаки
корней характеристического уравнения
определяют вид решения дифференциальных
уравнений. В частности, если
характеристическое уравнение имеет
действительные корни, то решение
дифференциального уравнения (или системы
дифференциальных уравнений) имеет
экспоненциальный вид. Это побуждает
нас заняться анализом корней уравнения
обратных часов.
Но вначале следует
уточнить одну немаловажную деталь:
отыскивая с самого начала именно
экспоненциальное решение для
дифференциального уравнения изменения
плотности нейтронов в виде одной
экспоненты — n(t) = no
exp (t / T), — мы невольно совершили небольшой
просчёт, который следует исправить по
ходу дела. Если уравнение обратных часов
имеет семь корней, то общее решение
системы дифференциальных уравнений
кинетики реактора будет не одной
экспонентой, а
будет представлять собой сумму семи
экспонент, показатели которых определяются
величинами этих семи корней уравнения
обратных часов:
n(t) = Aoexp(t/To)
+ A1exp(t/T1)
+ A2exp(t/T2)
+ A3exp(t/T3)
+ A4exp(t/T4)
+ A5exp(t/T5)
+ A6exp(t/T6)
или
в более краткой форме:
6
n(t)
= Aoexp(t/To)
+ S
Aiexp(t/Ti)
, (12.19)
i=1
где То,
T1,
T2,
… , T6
— значения семи корней уравнения обратных
часов, а Ao,
A1,
A2,
… , A6
— величины постоянных интегрирования,
находимые путём подстановки в общее
решение (12.19) конкретных начальных
условий.
Знаки корней
уравнения обратных часов наиболее
наглядно видны, если показать его решение
в графическом виде (см. рис.12.3).
Рис,12.1. График зависимости корней
уравнения обратных часов при положительных
и отри- цательных реактивностях
разной величины.
На этом графике
показано решение уравнения обратных
часов в зависимости не от величины
самого периода Т, а от обратной ему
величины 1 / Т: так удобнее выполнять
решение уравнения аналитически.
Как видим, функция
r
= f (1 / T) имеет шесть точек разрыва (второго
рода), и именно благодаря этой разрывности
отдельные корни уравнения обратных
часов отображаются на графике достаточно
наглядно: области изменения каждого из
семи корней по оси 1/T лежат между
соответствующими точками разрыва;
например, нулевой обратный корень 1/То
лежит правее первой точки разрыва (-
l1),
первый обратный корень 1/Т1
— между первой и второй точками разрыва
(-l1
и -l2),
второй обратный корень 1/T2
— между второй и третьей точками разрыва
(-l2
и -l3
) и так далее; значения последнего,
седьмого, обратного корня 1/Т7
— располагаются левее последней, шестой,
точки разрыва (-l6).
При этом знаки
всех семи корней уравнения обратных
часов определяются самым наглядным
образом: в точках пересечения
соответствующих участков графика с
горизонтальной прямой, отсекающей на
оси ординат рассматриваемое значение
реактивности r.
Из графика видно,
что, если величина сообщаемой реактору
реактивности положительна, то нулевой
обратный корень 1/То
, а, значит, и сам корень То,
— положителен (т.к. располагается в правой
полуплоскости, или правее оси О — r
). Остальные шесть корней (Т1
¸
Т6)
уравнения обратных часов — отрицательны
(лежат в левой полуплоскости).
Если же величина
сообщаемой реактору реактивности
отрицательна, то все семь корней уравнения
обратных часов отрицательны (лежат в
левой, отрицательной, полуплоскости).
Что касается
величин самих корней, то они, как следует
из графика, определяются только величиной
сообщаемой реактору реактивности r.
Теперь о знаках
постоянных интегрирования (Ао
¸
А6).
Здесь не приводится полный (и очень
громоздкий) аналитический вывод общего
выражения для любой из постоянных
интегрирования, которое имеет вид:
r
Ti
Аi
= __________________________ (12.20)
6
l
+ S
{libэi
/ [(1/Ti)
+ li]2}
i=1
Квадрат выражения
в квадратных скобках, независимо от
знака корня Тi
, всегда имеет положительный знак, и,
поскольку все остальные величины
знаменателя положительны, то весь
знаменатель (12.1.20) — всегда положителен.
А раз так, то знак постоянной интегрирования
Аi всегда
определяется знаком произведения rТi
в числителе правой части этого выражения.
То есть, если нулевой корень То
при r
>
0, как говорилось выше, положителен (То
>
0), то произведение rТо
>
0, а, следовательно, Ао
>
0. При отрицательной же величине
реактивности (r
<
0) произведение отрицательного нулевого
корня То
на отрицательную величину реактивности
r
даёт положительную величину произведения
rТо,
и, следовательно, величина нулевой
постоянной интегрирования будет иметь
положительный знак. Проделав такой
микроанализ со всеми величинами
постоянных интегрирования, можно прийти
к общему выводу:
при r>0:
То
>
0 и Ао
>
0, а остальные корни (Т1¸Т6)<0
и (А1¸А6)
<
0 (12.21)
при r<0:
все 7 корней (То¸Т6)<0,
а постоянные интегрирования (Ао¸А6)>0
(12.22)
б) Самостоятельное
практическое значение решения уравнения
обратных часов.
Анализ знаков
корней уравнения обратных часов и
постоянных интегрирования безусловно
важен, так как он даёт возможность
выявить качественную структуру и дать
физическое толкование характеру
переходных процессов при сообщении
реактору реактивности того или иного
знака.
Но значение
уравнения обратных часов не исчерпывается
только этим. Забегая немного вперёд,
заметим, что из семи корней уравнения
обратных часов старший корень То
(старший — в математическом понимании
этого слова, то есть — наибольший по
величине) имеет простое физическое
толкование: это
— тот самый установившийся период,
определяющий “чисто экспоненциальное”
изменение плотности нейтронов в реакторе
в развитой стадии переходного процесса
n(t). (Почему
это так, станет ясно немного позже).
Эту величину
установившегося периода, как уже
говорилось, легко измерить практически
с помощью самого обычного секундомера.
Вместе с тем, величина установившегося
периода (То)
для конкретного реактора в рассматриваемый
момент кампании определяется только
величиной сообщённой реактору реактивности
r,
следовательно, уравнение обратных часов
для конкретного реактора (с конкретной
величиной bэ)
устанавливает жёсткую однозначную
взаимосвязь величин реактивности r
и установившегося периода То
(или r
— с величиной установившегося периода
удвоения мощности реактора Т2,
которая, как мы знаем, пропорциональна
величине установившегося периода То).
А это значит, что
по величине измеренного установившегося
периода удвоения мощности можно находить
величину сообщённой реактору реактивности,
и, наоборот, — по величине сообщённой
реактору реактивности можно предсказывать,
с каким установившимся периодом удвоения
будет происходить установившийся разгон
(или спад) мощности ядерного реактора.
Это, согласитесь, практически очень
важно для оператора реакторной установки.
Эту взаимосвязь можно занести в программу
компьютера, можно выразить в форме
таблицы или в форме графика.
Рис. 12.2. Две наглядные формы взаимосвязи
реактивности реактора rи установившегося периода удвоения
мощности реактора Т2, вытекающие
из решения уравнения обратных часов.
Пользуясь
приведенными таблицей или графиком,
оператор имеет возможность быстро
оценить величину реактивности реактора
по измеренному периоду удвоения мощности
или предсказать величину установившегося
периода разгона реактора по величине
реактивности, которую он собирается
сообщить реактору.
-
Переходные
процессы при сообщении реактору
отрицательной
реактивности
-
Характер
переходных процессов n(t) при r
<
0. Так как
при сообщении реактору отрицательной
реактивности все семь корней уравнения
обратных часов отрицательны, это
означает, что общее решение системы
дифференциальных уравнений кинетики
представляет собой алгебраическую
сумму убывающих экспонент (любая
экспонента с отрицательным показателем
— убывающая). А поскольку (см. условие
(12.22)) все без исключения постоянные
интегрирования Аi
в случае отрицательной реактивности
положительны, то можно выразиться более
точно: при отрицательной реактивности
решение системы дифференциальных
уравнений кинетики есть арифметическая
сумма семи
убывающих экспонент, и если обозначать
через Тi
абсолютную величину корней уравнения
обратных часов, то:
6
n(t)
= Ao
exp(- t / To)
+ S
Ai
exp (- t / Ti)
(12.23)
i = 1
Геометрическое
суммирование семи убывающих экспонент
показано на рис.12.2. Как видим, переходный
процесс n(t) в “холодном” реакторе имеет
уже не тот моноэкспоненциальный вид,
который получался из решения элементарного
уравнения кинетики: здесь хорошо
просматриваются две стадии развития
переходного процесса, свойственные
реальным переходным процессам во всех
реакторах, а именно, — стадия начального
скачка, продолжительность которой
определяется временем, в течение которого
шесть младших экспонент спадают до
практического нуля, и стадия чисто
экспоненциального спада плотности
нейтронов, определяемая старшей,
экспонентой Ао
exp (- t / To),
показатель которой обратно пропорционален
наибольшему по абсолютной величине
корню уравнения обратных часов.
Рис.12.3. Экспоненциальные составляющие
переходного процесса n(t) при скачкообразном
сообщении критическому реактору
отрицательной реактивности.
Теперь смысл
названия установившегося
периода То
должен быть окончательно ясен.
Зависимость любого
(переходного) периода Тiпри
отрицательной величине сообщаемой
реактору реактивности имеет обратный
характер: чем больше абсолютная величина
сообщаемой реактору отрицательной
реактивности, тем меньше абсолютная
величина любого из корней уравнения
обратных часов Тi(что очень
наглядно иллюстрирует график решения
уравнения обратных часов). Следовательно,
крутизна переходных процессов n(t) в
реакторе определяется только величиной
сообщаемой реактору отрицательной
реактивности: чем больше абсолютная
величина отрицательной реактивности,
тем более круто идёт спад плотности
нейтронов n(t), причём, и на стадии
начального скачка, и на стадии последующего
экспоненциального спада.
Можно сказать и
иными словами: чем больше абсолютная
величина сообщаемой реактору отрицательной
реактивности, тем больше абсолютная
величина начального скачка.
Нелинейный характер
начальной стадии переходного процесса
ещё более наглядно иллюстрируется
графиком зависимости, построенным в
полулогарифмической системе координат
для различных значений отрицательной
реактивности.(рис.12.4):
Рис.12.4. Качественный вид переходных
процессов n(t) в натуральной и
полулогарифмической системах координат.
Логарифмирование
экспоненциальной функции даёт, как
известно, линейную зависимость,
изображаемую прямой линией, угловой
коэффициент которой численно равен
постоянному сомножителю в показателе
экспоненты, то есть, в данном случае, —
величине (- 1 / То).
Поэтому в полулогарифмической системе
координат прямой линией изображается
только вторая, чисто
экспоненциальная,
стадия переходного процесса n(t), а на
стадии начального скачка переходный
процесс выглядит нелинейно.
Наличие стадии
начального скачка в переходном процессе
n(t) физически объясняется тем, что при
скачкообразном сообщении критическому
реактору отрицательной реактивности
первыми всегда реагируют на это возмущение
мгновенные нейтроны: резко уменьшается
скорость генерации и резко возрастает
скорость их поглощения. И если бы к
моменту введения отрицательной
реактивности в реакторе не были бы
накоплены достаточно большие стационарные
концентрации предшественников
запаздывающих нейтронов всех групп,
процесс начального спада n(t) происходил
бы во много раз быстрее (поскольку время
жизни мгновенных нейтронов во много
раз меньше времени жизни запаздывающих
нейтронов любой группы), то есть это был
бы практически безынерционный бросок
n(t) вниз, почти синхронно отслеживающий
уменьшение величины коэффициента
размножения на мгновенных нейтронах.
Но предшественники запаздывающих
нейтронов в реакторе есть, и их стационарные
концентрации в критическом реакторе
достаточно высоки, а это значит, что в
первые секунды начального скачка
достаточно высоки и скорости их b-распада
(вспомните: dCi/dt
= — liCi),
а, значит, вначале высоки и скорости
генерации запаздывающих нейтронов всех
групп, и получается, что эти добавки
запаздывающих нейтронов в общий цикл
размножения тормозят общее падение
плотности нейтронов n(t), которое без них
было бы очень резким.
Но поскольку с
уменьшением n(t) синхронно уменьшается
и скорость деления ядер топлива, то с
той же синхронностью уменьшается и
скорость генерации предшественников
запаздывающих нейтронов всех групп, а
с некоторым запаздыванием — и скорость
генерации излучателей запаздывающих
нейтронов. Скорость уменьшения
концентраций ядер-предшественников
запаздывающих нейтронов не может стать
ниже скорости их b-распада
(равной liCi(t)).
Следовательно, экспоненциальный процесс
снижения концентрации предшественников
каждой группы (надеюсь, вы не сомневаетесь,
что он чисто экспоненциальный: ведь
решения 6 уравнений для концентраций
были найдены в виде Ci(t)
= Coi
exp(-t / Ti)
) не может идти с периодом, меньшим, чем
период распада предшественников каждой
группы (равным 1 / li).
Поэтому понятным становится и физический
смысл величины переходного периода Тi:
это — периоды экспоненциальных процессов
Сi(t),
описывающих переходы величин концентраций
предшественников запаздывающих нейтронов
от одного стационарного значения (Соi)
до другого (соответствующего концу
переходного процесса n(t). В частности,
судя по виду решения, конечной концентрацией
предшественников запаздывающих нейтронов
может быть и нулевая их концентрация.
Примечание. Обратим внимание с
самого начала на эту “несуразицу”: при
любом значении сообщаемой реактору
отрицательной реактивности концентрации
предшественников запаздывающих нейтронов
устремляются к нулю, то есть, в соответствии
с известным правилом, через (4¸5) периодов Тiвеличины концентраций
Сiдолжны обратиться в практический
ноль. Объяснение этому будет дано при
рассмотрении кинетики подкритического
реактора с независимым источником
нейтронов.
И лишь тогда, когда
скорость снижения n(t) ”вплотную”
снизится до скорости b-распада
предшественников самой долгоживущей
(первой) группы, переходный процесс n(t)
плавно переходит во вторую (чисто
экспоненциальную) стадию уменьшения
плотности нейтронов с установившимся
периодом То.
-
Величина
начального скачка при отрицательных
реактивностях.
Вопрос о величине начального скачка
при сообщении реактору отрицательных
реактивностей имеет не только чисто
теоретическое значение, но и представляет
большой практический интерес и для
конструктора реактора, и для
оператора-эксплуатационника. Он
возникает из приблизительно таких
соображений: отрицательные реактивности
сообщаются критическому реактору не
только ради снижения его мощности (для
этого нужны совсем небольшие величины
отрицательных реактивностей), но и для
выполнения быстрой (аварийной) остановки
реактора в случаях возникновения
ситуаций, угрожающих перерасти в аварию
реактора или какого-либо другого
элемента АЭУ. Для этого в реакторе
предусматривается аварийная защита.
В одних энергетических реакторах — это
специальные группы стержней-поглотителей,
автоматически «выстреливаемые” в
активную зону при возникновении
аварийных ситуаций; в большинстве
реакторов АЭС в качестве стержней АЗ
используются все штатные подвижные
поглотители (включая и регулирующие
группы), которые в нормальных условиях
находятся вне активной зоны (кроме
регулирующих групп), но по сигналу АЗ
вводятся в активную зону с максимальной
предусмотренной скоростью.
Одним словом,
стержни АЗ — как раз и есть те самые
поглотители, с помощью которых критическому
реактору за сравнительно короткое время
может быть сообщена сравнительно большая
отрицательная реактивность.
Из рис.12.4. мы уже
видели, что плотность нейтронов (или
нейтронная мощность реактора) при
сообщении реактору отрицательной
реактивности уменьшается тем более
высоким темпом, чем большая величина
отрицательной реактивности воздействует
на реактор. Величина начального скачка
тоже находится явно в прямой зависимости
от величины сообщаемой реактору
отрицательной реактивности. Вопрос
заключается в том, каков характер этой
зависимости.
Договоримся считать
условной величиной начального скачка
Dn¢
разницу величин начальной плотности
нейтронов no
и постоянной интегрирования Ао
старшей экспоненты Аоexp(-t/To):
Dn¢= no— Ao(12.24)
Конечно, (см.
рис.12.3) истинная величина начального
скачка (Dn)
несколько больше, чем величинаDn¢,
но даже такое приближение позволяет
качественно оценить предельные величины
начальных скачков. Из графика рис.12.3.
следует, что приближенная величина
начального скачка есть не что иное как
сумма всех постоянных интегрирования,
кроме Ао:
6
Dn¢
= S
Ai
= A1
+ A2
+ A3
+A4
+ A5
+ A6
i=1
Для большей общности
попытаемся найти зависимость от
реактивности величины относительного
начального скачка:
6
Dn¢/no
= (no
— Ao)
/ no
= 1 — Ao
/ no
= 1 — 1 / [1 + (S
Ai)
/ Ao]
(12.25)
i=1
Подставляя сюда
общее выражение для постоянной
интегрирования Аi
(12.20), после нескольких простейших
преобразований можно получить выражение:
Dn¢
/ no
= 1 — To
/ (To
+ T1
+ T2
+ T3
+ T4
+ T5
+ T6)
(12.26)
Теоретически
предельная (наибольшая) величина
начального скачка будет иметь место
при бесконечно большой по абсолютной
величине отрицательной реактивности
(то есть при r
®
— ¥
). Но при этом корни уравнения обратных
часов вплотную приближаются к своим
асимптотическим значениям (см. график
корней уравнения обратных часов):
То®
— 1 /l1,
T1®
-1 /l2,
T2
®
— 1 /l3,
T3
®
— 1 /l4,
T4
®
— 1 /l5,
T5
®
— 1 / l6,
T6
®
— l / dkэ
Примечание.
В числителе выражения для Т6 стоит
величина времени жизни мгновенных
нейтронов l, в отличие от прочих выражений,
в числителях которых стоят единицы.
Считаю своим долгом предупредить об
этом, поскольку эти два символа близки
по начертанию, и их можно перепутать.
Если подставить
эти значения в формулу (12.26), можно
получить величину предельного
относительного начального скачка при
отрицательной реактивности
(Dn¢
/ no)пред
0.639 (12.27)
Из этого следует
не слишком весёлый для оператора
реакторной установки вывод:
Реактор
сразу остановить нельзя!
Энергетический
реактор, как видим, является аппаратом
достаточно инерционным не только в
тепловом, но и в нейтронно-физическом
отношении, и единственным утешением
оператору может служить только то, что
для избежания аварии в подавляющем
большинстве случаев срабатывания
аварийной защиты полного сброса мощности
до нуля не требуется. Однако, это не
умаляет нашего практического интереса
к следующему закономерно возникающему
у практика вопросу: а что же дальше?
сколь интенсивен темп дальнейшего
снижения мощности реактора после
начального скачка?
-
Предельный темп
снижения мощности реактора после
завершения начального скачка.
С окончанием начального скачка процесс
снижения плотности нейтронов (нейтронной
мощности) реактора идёт по экспоненциальному
закону n(t) = Aoexp
(-t / To),
то есть темп снижения определяется
величиной старшего (наибольшего по
абсолютной величине) корня уравнения
обратных часов То.
Поведение
величины То
при различных величинах сообщаемой
реактору отрицательной реактивности
легко прослеживается по самой правой
ветви графического решения уравнения
обратных часов: при r®
— ¥
величина (1 / To)
®
— l1,
то есть сама абсолютная величина корня
То
устремляется к величине (1 / l1).
Следовательно, предельный темп снижения
мощности реактора после начального
скачка при сообщении реактору очень
большой (по абсолютной величине)
отрицательной реактивности
Тоmin
= 1 / l1
= 1 / 1.263. 10 -2
»
79.2 c (12.28)
Физическое
толкование этого ограниченного темпа
снижения плотности нейтронов после
завершения начального скачка кажется
вполне очевидным: c таким периодом идёт
b-распад
самой долгоживущей группы предшественников
запаздывающих нейтронов, и обогнать
этот темп плотность нейтронов в реакторе
не в состоянии.
Так как любая
убывающая экспонента достигает своего
практического нуля через 4 ¸
5 своих периодов, то можно оценить время
спада нейтронной мощности реактора до
практического нуля с момента окончания
начального скачка. Оно приблизительно
составит
5
.
79.2 »
400 с »
6.6 мин
Так обстоит дело
в гипотетическом случае сообщения
критическому реактору
бесконечно-большой величины отрицательной
реактивности. И ясно, что в реальных
случаях сообщения реактору более
умеренной величины отрицательной
реактивности темп снижения мощности
по завершении начального скачка будет
ешё более медленным (то есть величина
установившегося периода То
будет ещё большей). Например, при
срабатывании быстродействующей аварийной
защиты с физическим весом всего в — 2.5%
(то есть сообщающей критическому реактору
при полном вводе в активную зону величину
отрицательной реактивности r
= — 0.025 ) величина установившегося периода
спада мощности после начального скачка
оказывается равной около 92 с, а при r
= — 0.010 — величина То »
96 с.
Эти числовые
примеры подталкивают к практическому
выводу о том, что нет никакого смысла
снабжать реактор аварийной защитой
большого физического веса из одного
стремления увеличить её быстродействие:
увеличение физического веса стержней
аварийной защиты свыше 3% вообще
нецелесообразно, поскольку заметного
выигрыша в быстродействии АЗ при этом
не наблюдается. Поэтому при выборе
физического веса системы АЗ обычно
руководствуются другими практическими
соображениями.