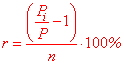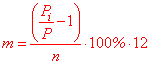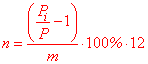Что нужно знать при расчете процентов по вкладам (депозитам)
Рано или поздно перед нами встает вопрос о расчете процентов по банковским вкладам (депозитам).
В банковском деле существует два способа начисления процентов:
- по формуле простых процентов;
- по формуле сложных процентов.
Расчет процентов по формулам может совершаться с использованием плавающей и фиксированной процентной ставки.
Фиксированная ставка — процентная ставка, которая остается постоянной на весь срок размещения вклада. Как правило, ставка может быть изменена в момент пролонгации (продления) договора, выплате процентов при досрочном расторжении договора.
Плавающая ставка — процентная ставка, которая может меняться во время размещения вклада. Условия и порядок изменения ставки оговариваются в договоре (например, такими условиями могут быть изменение ставки рефинансирования, изменение курсов валют и т.п.).
Для того, чтобы начать расчет, нам необходимо знать следующие параметры депозита:
- сумма вклада;
- годовая процентная ставка;
- период начисления процентов по депозиту;
- срок размещения депозиа;
- вид процентной ставки — фиксированная или плавающая.
Формула начисления простых процентов
Расчет наращенной суммы вклада
Данной формулой необходимо воспользоваться если начисление процентов происходит в конце действия депозита.
S = P × (1 + n × i),
где S — наращенная сумма;
P — сумма вклада (первоначальная сумма);
n — период размещения вклада;
i — годовая процентная ставка.
Пример расчета наращенной суммы по формуле простых процентов
Первоначальная сумма вклада P = 45000 руб. помещена в банк на n = 2 года под i = 15% годовых. Определим наращенную сумму после двух лет
S = 45000 × (1 + 2 × 0,15) = 58500 руб.
Следовательно, за два года размещения вклада в данном случает доход составит 13500 руб.
Расчет периода начисления вклада
Зная первоначальную сумму вклада P, наращенную сумму S, простую годовую процентную ставку i, можно определить период начисления
n = (S — P)/(i × P).
Данной формулой возможно воспользоваться, например, в случае расчета времени начисления необходимой нам суммы.
Пример расчета периода начисления по формуле простых процентов
Первоначальная сумма P = 10000 руб., необходимо нарастить сумму S до 20000 руб., i = 20% годовых. Определим какой период времени нам понадобится для получения 20000 руб.
n = (20000 — 10000)/(0,2 × 20000) = 2,5 года.
Определение простой годовой процентной ставки
Чтобы определить необходимую нам процентную ставку воспользуемся формулой
i = (S — P)/(n × P).
Пример расчета простой процентной ставки
Имеем первоначальную сумму 30000 руб., необходимо ее нарастить (заработать) до 35000 руб, предполагаем разместить на 1 год. Определим необходимую нам процентную ставку
i = (35000 — 30000)/(1 × 30000) = 16,7%.
Расчет наращенной суммы при плавающей процентной ставки
Если процентная ставка по депозиту менялась в течении срока размещения, то воспользуемся формулой
S = P × (1 + n1 × i1 + n2 × i2 + … + n k × ik).
Пример расчета наращенной суммы при плавающей процентной ставки
Первоначальная сумма вклада P = 75000 руб., в первой половине года применялась простая процентная ставка 7,5% годовых, во второй половине года — 9,5% годовых. Определим наращенную сумму по вкладу в конце года
S = 75000 × (1 + 0,5 × 0,075 + 0,5 × 0,095) = 81375 руб.
Формула начисления сложных процентов
Формула сложных процентов применяется при капитализации процентов (начисления процентов на проценты), т.е. начисление процентов по депозиту происходит через равные промежутки времени, а начисленные проценты прибавляются ко вкладу.
Расчет наращенной суммы вклада (сложные проценты)
Наращенная сумма при периоде начисления в годах определяется
S = P × (1 + i)n.
Пример расчета наращенной суммы при сложных процентах
Первоначальная сумма вклада P = 25000 руб., помещена в банк на n = 3 года под i = 7,5% годовых. Определим наращенную сумму
S = 25000 × (1 + 0,075)3 = 31057 руб.
Расчет периода начисления в годах при сложных процентах
Если мы знаем первоначальную сумму вклада P, наращенную сумму S и сложную годовую процентную ставку i, то определим период начисления n (в годах) по формуле
n = ln(S/P)/ln(1 + i).
Пример расчета периода начисления при сложных процентах
Первоначальная сумма вклада P = 27500 руб., наращенная сумма S = 33700 руб., i = 10% годовых. Определим за какой период была начислена сумма
S = ln(33700/27500)/ln(1 + 0,1)= 2,1 года.
Расчет годовой процентной ставки при сложных процентах
Определить годовую процентную ставку при сложных процентах можно по формуле
i = n√S/P — 1.
Пример расчета годовой процентной ставки при сложных процентах
Первоначальная сумма вклада P = 75000 руб., наращенная сумма S = 97000 руб., период начисления n = 2 года. Определим процентную ставку
i = 2√97000/75000 — 1 =0,136 = 13,6%.
Расчет наращенной суммы при плавающей процентной ставки сложных процентов
S =P × (1 + i1)n1 × (1 + i2)n2 × … × (1 + in)nk
Пример расчета наращенной суммы при плавающей процентной ставки сложных процентов
Первоначальная сумма вклада P = 35000 руб., n1 = 2 года применялась сложная процентная ставка i1 = 10% годовых, затем n2 = 3 года применялась сложная процентная ставка i2 = 12% годовых. Определим наращенную сумму
S =35000 × (1 +0,1)2 × (1 +0,12)3 = 59498 руб.
Начисление сложных процентов несколько раз в году
Если начисление сложных процентов происходит несколько раз в году, то воспользуемся формулой
S = P × (1 + j/m)n×m
где j — номинальная процентная ставка; m — интервал начисления.
Пример начисление сложных процентов несколько раз в году
Первоначальная сумма инвестирования 62000 руб., период начисления 3 года, сложная процентная ставка j = 9% годовых ежеквартально, m = 4, т.к. в году 4 квартала. Определим наращенную сумму.
S = 62000 × (1 +0,09/4)3×4 = 80975 руб.
Загрузка…
Задача 1
Определите,
какой из вариантов кредитования (по уровню доходности по ставке простых
процентов) наиболее выгоден для заемщика:
— сумма
первоначального долга 120000 рублей; срок кредитования 250 дней; наращенная
сумма долга 130000 рублей;
— сумма
первоначального долга 120000 рублей; срок кредитования 180 дней; наращенная
сумма долга 128000 рублей;
— сумма
первоначального долга 120000 рублей; срок кредитования 320 дней; наращенная
сумма долга 136000 рублей;
Задача 2
Клиент взял
в банке кредит на 180 дней по номинальной ставке 16% и в конце срока вернул всю
сумму долга с процентами, что составило 310 тыс. руб. Определить сумму
выданного кредита.
Задача 3
На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.
Задача 5
5 июня клиент взял кредит 200 тыс. руб. При
погашении кредита единым платежом клиент заплатил 230 тыс. руб. Определить срок
операции и дату погашения кредита, если в операции использовалась простая
процентная ставка 18% годовых (точные проценты с фактическим сроком операции).
Задача 6
Через 120
дней с момента подписания кредитного договора заемщик должен вернуть банку 750
тыс. руб. Процентная ставка по кредиту равна 18% годовых. Чему равна
первоначальная сумма долга?
Задача 7
Банк
принимает депозиты на 3 месяца по ставке 50% годовых, на 6 месяцев по ставке
70% годовых и на год по ставке 90% годовых. Определить суммы, которые может
получить владелец депозита 4500 руб., выбрать наиболее выгодный вариант
размещения вклада.
Задача 8
Банк
объявил следующие условия выдачи ссуды на один год: за первый квартал ссудный
процент 50%; за второй квартал – 75%; за третий – 100%; за четвертый квартал –
125%. Определить сумму к возврату в банк, если ссуда составляет 200000 руб.
Задача 9
Найдите
простой процент, начисленный за четыре месяца по ставке 1% на сумму 10 тыс.
руб.
Задача 10
Ссуда в
размере 50 тыс. руб. была выдана на полгода при условии начисления на нее
простых процентов по ставке 20%. Определите сумму погашения.
Задача 11
Банк
начисляет 10 тыс. руб. за использование 800 руб. в течение 60 дней. Найдите
простую процентную ставку, если применяются обыкновенные проценты.
Задача 12
Какая
сумма необходима для того, чтобы накопить за пять лет 70 тыс. руб., если на эту
сумму будут начисляться простые проценты по ставке 8%?
Задача 13
За
сколько дней сумма 800 тыс. руб. увеличится до 900 тыс. руб., если на исходную
сумму начисляются обыкновенные простые проценты по ставке 9%?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Сумма 100
тыс. руб. была получена в долг 20 января с условием начисления на нее точных
простых процентов по ставке 25% и возвращения денег через год в сумме 120 тыс.
руб. Определите дату погашения долга, если год високосный.
Задача 15
В один и
тот же день в банк были вложены сумма 20 000 руб. под 4 % годовых и сумма 18
000 руб. под 5 % годовых. Вычислите, через сколько лет оба дохода будут
одинаковыми.
Задача 16
Ставка процентов банка по вкладам до
востребования, составлявшая в начале года 10% годовых, через полгода была
снижена до 8% годовых, а еще через 3 месяца до 6% годовых. Определите общую сумму, полученную клиентом банка
через год, если им был внесен вклад в размере 10 тыс. руб.
Задача 17
Банк
предлагает разместить вкладчику 700 000 руб. на срочный депозит в трех
вариантах: а) на 1 день под 6% годовых с последующим реинвестированием
ежедневно в течение месяца; б) на 10 дней под 10% годовых с последующим
реинвестированием каждую декаду в течение месяцев; в) на 1 месяц под 18%
годовых. Определить наиболее выгодный вариант вложения денежных средств.
Задача 18
Какая сумма была внесена на счет в
банке, если по истечении 5 лет на счета стало 5200 руб. Начисление процентов
осуществлялось по схеме простых процентов по ставке 10% за каждое полугодие?
Задача 19
Ссуда в
размере 10 тыс. руб. выдается по учетной ставке простых процентов 8% годовых.
Определить срок ссуды в годах, если заемщик хочет получить 9,5 тыс. руб.
Задача 20
Проценты
по ссуде размером 5 тыс. р., выданной на два месяца, составила 125 р. Какова
процентная ставка?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Кредит для покупки товара на сумму
50 тыс. руб. открыт с 12.02 до 02.10 включительно под 18% годовых. Какую сумму
заплатит должник в конце срока при начислении простых процентов? (временная база — ACT/360)
Задача 22
Найти простой процент для 7000 руб.
за пять месяцев при 3% годовых.
Задача 23
Какой капитал, будучи отдан в рост
под 7,5%, обратится через год вместе с процентными деньгами в 1343 рубля 75
копеек?
Задача 24
Ссуда
800000 руб. выдана на квартал по простой ставке процентов 20% годовых.
Определить наращенную сумму.
Задача 25
Какую сумму необходимо положить в
банк на 9 месяцев, чтобы накопить 900 руб., если он принимает вклады на
условиях 30% годовых?
Задача 26
Определите размер наращенной суммы
за один год, если первоначальная сумма равна 10 тыс. руб., первые полгода
годовая ставка простых процентов равна 18%, а вторые 21%.
Задача 27
Вклад в размере 250 000 руб.
помещен в банк по ставке 15% годовых. Спустя некоторое время получатель снял со
своего вклада 290 000 руб. Необходимо найти срок размещения вклада в
банке.
Задача 28
Через сколько лет сумма вклада
утроится, если банк работает по ставке 18% годовых.
Задача 29
Банк «Российский кредит» принимает
вклады до востребования по простой ставке 40% годовых. Определить сумму
начисленных процентов и сумму долга с начисленными процентами на вклад 2000 руб.,
размещенный на полгода.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 30
Вкладчик положил в банк 3000 руб.,
который выплачивает в год 6% (простых). Какая сумма будет на счету вкладчика
через 170 дней?
Задача 31
В банк было положено 150000 руб.
Сколько процентов (простых) выплачивает банк в год? Если через 2 года 9 месяцев
на счету было 270000 руб.
Задача 32
Найти
сумму начисленных простых процентов I и конечную сумму S, если
вклад P=1107.08 руб. размещен на t=10 месяцев при годовой
ставке i=70.7%.
Задача 33
Сколько
дней t понадобится, чтобы сумма в P=2228.23 рублей
«заработала» I=2.77 рублей, если она инвестируются при ставке i=23.7%
обыкновенного простого процента?
Задача 34
В банк положены на срочный
сберегательный счет 10000 руб. на 2 года по простой ставке 9% годовых с
дальнейшей пролонгацией на последующие 3 года по простой ставке 5% годовых:
а) Найдите наращенную сумму по
истечении 5 лет;
б) Найдите наращенную сумму по
истечении 5 лет, если через 2 года вклад изымается и кладется на новый счет на
3 года по простой ставке 5% годовых.
Укажите, какой вариант является
более предпочтительным а) или б)
Задача 35
Вами открыт вклад под 21% годовых.
На него начислен процентный платеж в сумме 21 тыс. руб. Найдите величину
вклада, если он был открыт на 21 год.
Задача 36
Ссуда в размере 30 000 руб. выдана
на полгода по простой ставке 100% годовых. Определить наращенную сумму.
Задача 37
Определите годовую ставку простых
процентов, при которой сумма в 5 тыс. руб. за три квартала возрастет до 6,5
тыс. руб.
Задача 38
В банк помещен капитал под 20%
годовых (обыкновенные проценты). По истечении 270 дней его величина составила
575 тыс. руб. Определить величину помещенного в банк капитала и сумму
начисленных процентов.
Задача 39
Банк
принимает депозиты на 3 месяца по ставке 15% годовых, на 8 месяцев по ставке
17% годовых и на год по ставке 19% годовых. Определить суммы, которые может
получить владелец депозита 14500 руб. Выбрать наиболее выгодный вариант
размещения вклада.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 40
Определить
срок в годах, при начислении простых процентов, по следующим данным:
Процентная
ставка 18%
Вклад –
2000 руб.
Вклад с
процентами – 10200 руб.
Задача 41
По
контракту кредитор предоставил в долг 60000 руб. Заемщик должен уплатить 70000
руб. через 90 дней. Определить доходность финансовой операции для кредитора в
виде процентной ставки i простых процентов.
Задача 42
Годовая ставка простых процентов в
банке составляет 12%. Через сколько лет вложенная сумма а) удвоится; б)
утроится?
Задача 43
В банк
положено 10000 руб., а через 2,5 года на счете было 120000 руб. Определить
ставку процентов банка.
Задача 44
За
сколько лет удвоится сумма долга, если применяется простая годовая ставка 17%?
Задача 45
При
открытии сберегательного счета при ставке 8% годовых 20 апреля на счет была
положена сумма 1 млн. рублей. Затем 5 июля этого же года было добавлено 500
тыс. руб. 10 сентября сняли сумму 750 тыс. рублей, а 20 ноября того же года
счет был закрыт.
Какую
сумму получил вкладчик при закрытии счета?
Задача 46
Какую
сумму надо положить в банк, выплачивающий 4% простых в год, чтобы получить 50
тыс. руб. а) через 4 месяца, б) через 1 год, в) через 2 года 9 месяцев?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 47
Договор
предусматривает следующие ставки простых процентов: за первый квартал j1=20%, за второй квартал j2=18%, за третий квартал j3=16%, за четвертый квартал j4=14%. Определить
коэффициент наращения за год.
Задача 48
Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.
Задача 49
На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?

Если нравится — подписывайтесь на телеграм-канал Бробанк.ру и не пропускайте новости
Высшее образование в Международном Восточно-Европейском Университете по направлению «Банковское дело». С отличием окончила Российский экономический институт имени Г.В. Плеханова по профилю «Финансы и кредит». Десятилетний опыт работы в ведущих банках России: Альфа-Банк, Ренессанс Кредит, Хоум Кредит Банк, Дельта Кредит, АТБ, Связной (закрылся). Является аналитиком и экспертом сервиса Бробанк по банковской деятельности и финансовой стабильности. rusanova@brobank.ru
Открыть профиль
Специалист сервиса Бробанк.ру в этой статье расскажет о простой формуле. Разберем формулу простого расчета процентов, как ею пользоваться и как провести расчет вклада. После этого останется только подставить свои цифры. Также расскажем, от чего зависят ставки по депозитам.
-
Как банки начисляют проценты по вкладам
-
Как выглядит формула простых процентов по вкладу
-
Как рассчитать вклад на специальном калькуляторе
-
Считаем вклад Тинькофф по простой формуле
-
Считаем вклад Тинькофф по сложной формуле
-
Что влияет на ставку по вкладу
Как банки начисляют проценты по вкладам
Процентная ставка — показатель доходности депозита. Сравнивая вклады в разных банках, вы смотрите на ставки. В каком она больше, тому и отдаете предпочтение. Но сам показатель процента не говорит о том, какой именно доход будет в итоге получен вкладчиком.
Ставка 8% годовых не значит, что вы получите 8% прибыли. Точный доход зависит от срока договора, формулы расчета процентов и операций, которые вкладчик проводит со счетом.
Варианты формул расчета:
- Простая. Применяется, когда банк начисляет доход по вкладу и передает его вкладчику. Начисление проводится ежемесячно, ежеквартально, ежегодно или в конце срока. Клиент получает деньги и распоряжаться ими на свое усмотрение.
- Сложная. Применяется для вкладов с капитализацией. Банк каждый месяц или квартал начисляет проценты, которые остаются на счете, увеличивая сумму вклада. В итоге доход становится выше.
Банк указывает ставку в годовом эквиваленте. Но срок вклада может составлять 3, 6, 9, 18 месяцев и так далее. Поэтому за основу можно брать доход за месяц. Например, если это ставка 8% годовых, ежемесячная прибыль составит 8/12, то есть округленно 0,67%. Такой вариант расчета прибыли можно использовать, если сумма вклада не меняется весь срок.
Как выглядит формула простых процентов по вкладу
Если по депозиту нет капитализации, проценты сразу выдают вкладчику или выплачивают по окончании срока размещения, при расчете дохода применяется формула простого процента.
Она выглядит так:
Подпись: Так выглядит формула простых процентов по вкладу.
Расшифровка формулы:
S — прибыль вкладчика
P — сумма вклада
I — процентная ставка
T — количество дней вклада
K — количество дней в году
Теперь рассчитаем прибыль вкладчика по простой формуле. Для примера возьмем депозит Газпромбанка «Копить»:
- 500 000 рублей;
- на 181 день;
- ставка для этого срока — 7,48% годовых;
- капитализации нет;
- доход клиент получит в конце срока.
Подставляем значения в формулу простых процентов по вкладу:
(500000 × 7,48 × 181 )/ 366 : 100 = 18495.
Сумма начисленных процентов составит 18 495 рублей. Именно столько получит вкладчик, если выберет вариант получения дохода одной суммой в конце срока.

Но вкладчик Газпромбанка может выбрать вариант получения процентов ежемесячно. В определенное число каждого месяца банк будет переводить ему начисленный доход на расчетный счет или карту.
В этом случае в срок подставляем количество дней в текущем месяце. Например, для мая, в котором 31 день, расчет будет таким:
(500000 × 7,48 × 31 / 366) : 100 = 3167
Если в месяце 30 дней, клиент получит 3065 рублей.
Каждый месяц потенциальный вкладчик будет получать от Газпромбанка 3167 или 3065 рублей.
Если речь о вкладе с возможностью пополнения или снятия, каждый месяц сумма может быть разной, поэтому и размер дохода не будет постоянным. Каждый месяц проводится отдельный расчет.
| Сумма от | 15 000Р |
| Проц. ставка | До 9,5% |
| Срок | До 3 лет |
| Макс. сумма | Любая |
| Пополнение | Нет |
| Снятие | Нет |
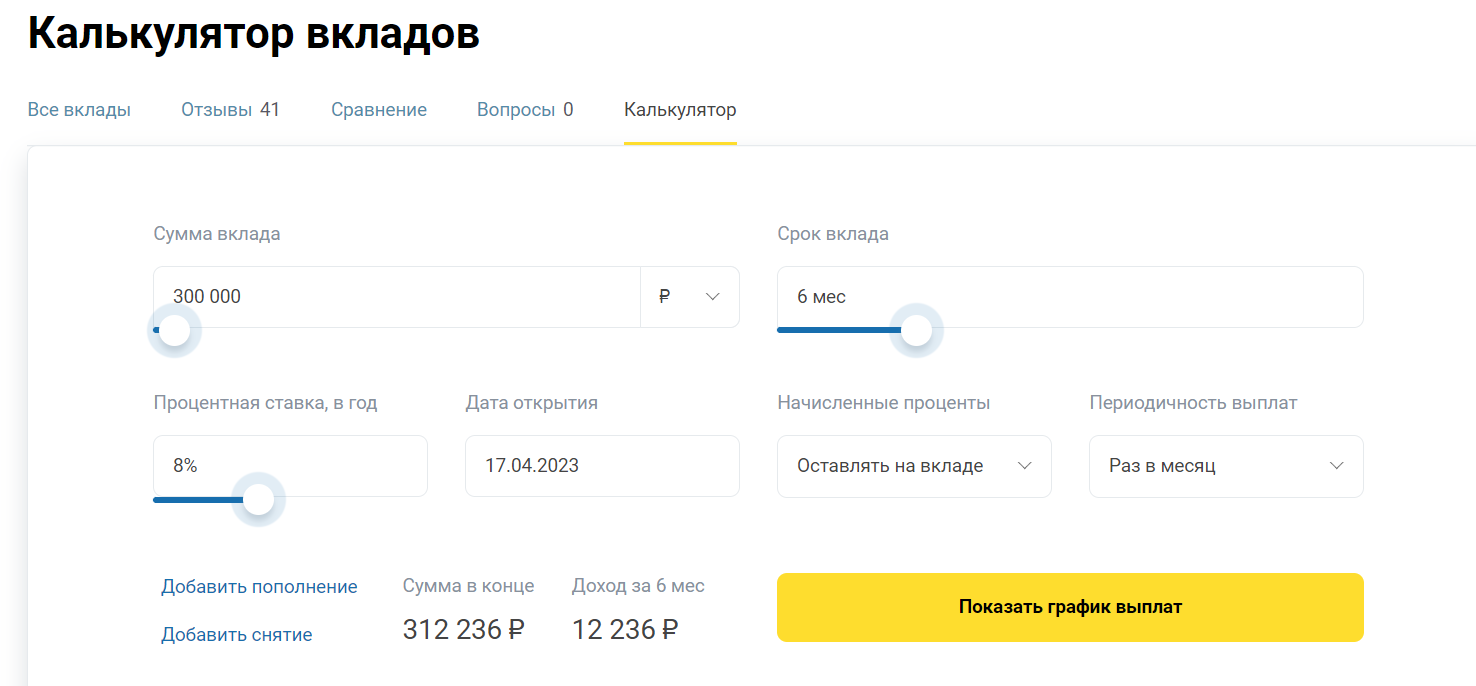
Как рассчитать вклад на специальном калькуляторе
На практике не обязательно знать формулу расчета процентов. Банки начисляют доход честно, применяя сложные или простые проценты. А вкладчики пользуются калькуляторами вкладов, в которые уже запрограммированы все формулы и схемы расчетов.
Сервис Бробанк.ру разработал калькулятор вкладов, которым все могут пользоваться бесплатно. Для расчетов переходите на страницу калькулятора.
Он выглядит так:
Так выглядит калькулятор расчета доходности вкладов на Бробанк.ру.
Для верного расчета определенного вклада внимательно изучите сетку тарифов. Не используйте процент, указанный как максимальный. В тарифах найдете точное значение для выбранного срока.
Считаем вклад Тинькофф по простой формуле
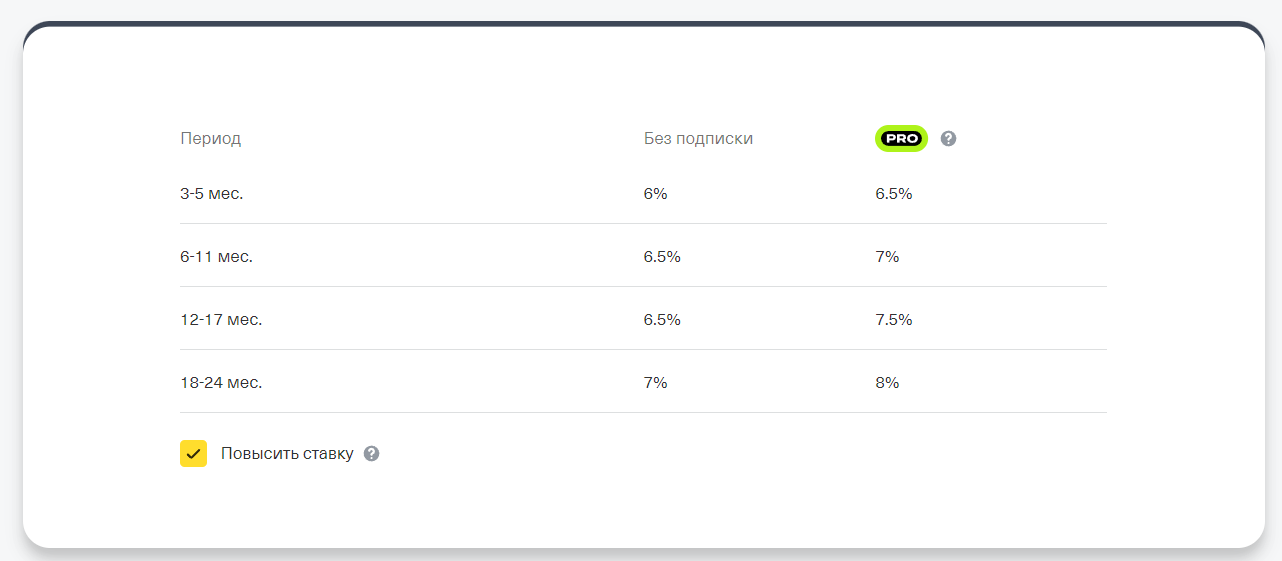
Например, вас заинтересовал вклад Тинькофф, годовая ставка в котором зависит от срока и от наличия у клиента подписки ПРО.
Ставки по вкладам в банке Тинькофф на момент создания материала — на апрель 2023 года.
Рассчитаем на универсальном калькуляторе доходность вклада Тинькофф со следующими параметрами:
- размер вложений — 500 000 рублей;
- договор заключается на 18 месяцев;
- у клиента нет подписки ПРО, ставка — 7%;
- выплата процентов — раз в месяц.
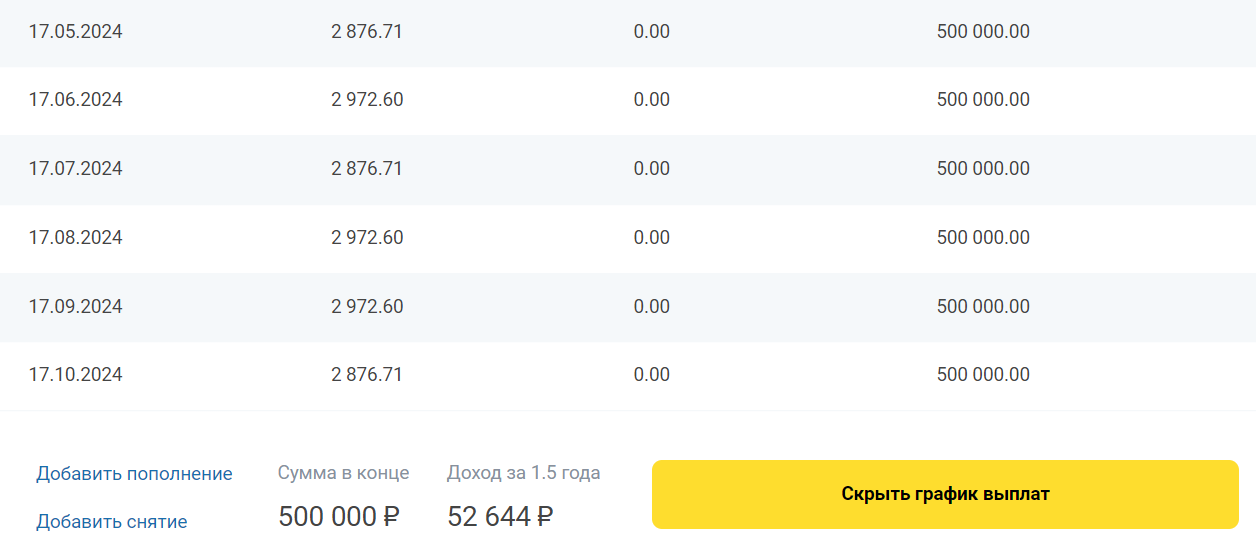
Вносим эти данные в калькулятор, и сразу видно, какую прибыль принесет открытие депозита в Тинькофф на 1,5 года — 52 644 рубля.
Пример расчета вклада Тинькофф на калькуляторе Бробанк по формуле простого процента.
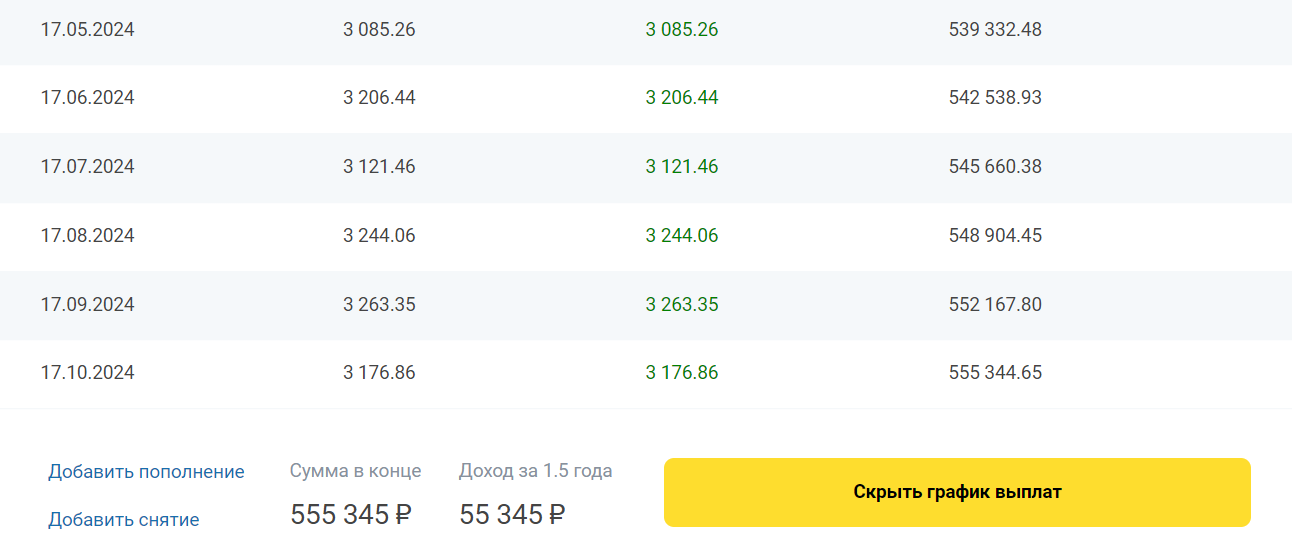
Считаем вклад Тинькофф по сложной формуле
С капитализацией калькулятор считает прибыль по формуле сложных процентов. В этом случае в опциях выбирайте вариант «Оставлять проценты на вкладе». Расчет процентов будет таким:
Пример расчета вклада Тинькофф на калькуляторе Бробанк по формуле сложного процента.
С капитализацией доход составит 55 345 рублей, без нее — 52 544. Делаем вывод — сложный вариант начисления процентов более выгодный для вкладчика, чем простой. По возможности лучше выбирайте программы с капитализацией.
| Сумма от | 50 000Р |
| Проц. ставка | До 8% |
| Срок | До 2 лет |
| Макс. сумма | 30 млн руб. |
| Пополнение | Возможно |
| Снятие | Возможно |
Что влияет на ставку по вкладу
На прибыль по вкладу влияет не формула расчета процентов, а характеристики вклада и сетка тарифов по программе. Наиболее выгодный вариант размещения средств — классический вклад без снятия и пополнения. Менее выгодный — с частичным снятием.
Ставки по вкладу зависят:
- от срока. Для каждого возможного срока по программе может быть установлена своя ставка;
- от суммы на счете. Например, если на счете лежат 100 000 рублей, процент один, а если 1 000 000 — другой;
- от схемы выплаты процентов: ежемесячно, в конце срока, сразу наперед при открытии счета;
- от клиента. Зарплатным клиентам банки часто увеличивают процент;
- от способа открытия вклада. Некоторые банки увеличивают ставку, если клиент открывает депозит онлайн.

Так что, смотрите не на формулу расчетов процентов, а на сетку тарифов по выбранной программе. А для анализа дохода используйте универсальный калькулятор вкладов на Бробанк.ру — он считает по тем же простым и сложным формулам.
Частые вопросы
Когда банки делают расчет процентов по вкладу по простой формуле?
Если речь о вкладе без капитализации, банк рассчитывает прибыль, когда вкладчик получает проценты на руки, или они выплачиваются банком в конце срока.
Какой вариант расчета выгоднее?
По сложной формуле расчет более выгоден для вкладчика. Если он не забирает проценты, они ежемесячно суммируются с телом вклада и прибыль становится больше.
Можно ли при открытии вклада выбрать формулу расчета процентов?
Нет, это происходит автоматически. Если вклад без капитализации, используется простая формула. Если с ней — сложная.
По какой формуле делается расчет после пролонгации?
Если в предыдущий период расчет велся по простой формуле, после пролонгации ничего не изменится. Договор продлевают на тех же условиях, поменяться может только ставка — устанавливается та, что действует на день пролонгирования.
Можно ли изменить схему начисления процентов?
Нет. Какие условия были установлены при заключении договора, такие и будут действовать весь срок вклада.
Комментарии: 0
/formula-rascheta-procentov-po-vkladam.jpg)
Общая формула расчета процентов по вкладу
Формула для вкладов с ежемесячной капитализацией
Формула для вкладов с ежедневной капитализацией
Формула для вкладов с ежеквартальной капитализацией
Что такое эффективная ставка по депозиту?
Как рассчитать через Excel?
Налоги на доход по вкладам
Подробнее про формулу
Банки в своей практике руководствуются несколькими формулами, позволяющими рассчитывать простые % и сложные. При их начислении применяется фиксированный и плавающий вид ставок. Фиксированную закрепляют договором при размещении вклада, она не меняется до конца периода его действия. Она может измениться в случае автоматических пролонгаций действия договора. Также она изменится в случае досрочного разрыва соглашения между клиентом и банком с выплатой % за фактический период размещения вложений, если вклад был размещен до востребования. Эти нюансы должны быть описаны в договорах.
В случае плавающих ставок, установленных изначально, их размер может изменяться на протяжении действия договоров.
При каких условиях и в каком порядке будет осуществляться этот процесс, нужно описывать в договорах. Изменение процентов привязано к изменениям:
- ключевой ставки;
- валютного курса;
- переводом депозита в иную категорию и др.
Для расчетов указываются все требуемые формой данные:
- сумма вклада;
- размер % ставки конкретного вклада;
- периодичность начислений % (поквартально, помесячно, ежедневно и др.);
- срок заключения договора;
- иногда нужно знать вид применяемой ставки – она может плавать или быть зафиксированной.
Общая формула расчета процентов по вкладу
Использование формулы простых процентов целесообразно в случае начисления процентов в конце срока размещения депозита или если они будут переводиться на отдельный счет – если капитализация договором не предусмотрена.
Выбирая вклад, клиент банка должен обратить внимание на порядок, который применяется при начислении процентов.
Формула расчета простых:
S = (P x I x t / K) / 100
Обозначения:
- S – прибыль со вклада (только проценты, без тела вклада);
- P – сумма, изначально внесенная на депозит;
- I – размер % ставки (за год);
- t – кол-во дней начисления %;
- K – кол-во дней за год по календарю.
A = P * (1 + r/n)^(n*t)
Здесь все более сложно, поскольку нужно высчитывать степень (^ – знак степени). Остальные обозначения:
- A – общая сумма денег (тело вклада + проценты), которую вы получите после того, как срок вклада закончится.
- P – стартовая сумма, которую вы кладете на счет вклада.
- r – процентная ставка по вкладу.
- n – количество расчетов прибыль в году, для ежедневной капитализации – 365 или 366, для ежемесячной – 12 и так далее.
- t – количество лет вклада. 6 месяцев – это 0.5 года.
Формула для вкладов с ежемесячной капитализацией
Чтобы рассчитать возможную прибыль в случае выбора вида депозита с капитализацией % с ежемесячным начислением % подойдет такая формула:
S = Р * (1 + (N/100)/12)^n, здесь используются следующие обозначения:
n – количество проведенных операций перевода процентов в тело вклада на протяжении полного срока действия договора (то есть месяцев вклада);
S – сумма вклада на дату окончания действия депозита, которую вкладчик получит на руки;
Р – изначально внесенная сумма на депозит с возможностью капитализации;
N — % ставка (годовая).
Формула для вкладов с ежедневной капитализацией
Если выбрана форма начисления % с ежедневной капитализацией, применяется следующая формула:
S = P * (1 + (N/100)/K)^T, где:
S – суммарный доход (тело вклада + проценты);
Р – внесенная при заключении договора сумма;
N – годовая % ставка;
К – 365 или 366 дней;
Т – кол-во дней, на которые открыт депозит.
Формула для вкладов с ежеквартальной капитализацией
В данном случае расчет процентов будет выглядеть следующим образом:
S=Р * (1+ (N/100)/4)^Т, где:
S — получаемый в конце срока доход (тело вклада + проценты);
Р – изначально размещенная сумма на депозите;
N — годовой %;
Т – количество кварталов, на протяжении которых открыт вклад.
Что такое эффективная ставка по депозиту?
Эффективная ставка = фактическая ставка + прибыль от капитализации. Если вклад – без капитализации, то эффективная ставка равна фактической ставке (указана в договоре); если вклад – с капитализацией, то эффективная ставка будет выше фактической, поскольку капитализация будет увеличивать тело вклада.
Как рассчитать через Excel?
Рассчитать в Excel доход от депозита можно на примере. Если необходимо положить на депозит 50 000 руб. с процентной ставкой 8% на три года с ежемесячной капитализацией и просчитать размер дохода через 24 месяца, нужно составить таблицу:
- A1-A24 – указываем месяцы, то есть 1,2,3…
- D1 – указываем сумму тела кредита.
- D2 – указываем ставку в процентах
Теперь нужно в ячейку B1 вставить специальную формулу для подсчета сложного процента: =БС($D$2/12;A1;;-$D$1). Первый аргумент ($D$2/12) – проценты, нужно делать на 12, поскольку считаем ежемесячное начисление. Второй аргумент (A1) – месяц, за который считаем. Третий аргумент оставляем пустым (комиссии/сборы). Четвертый (-$D$1) – тело вклада, ввиду некоторых особенностей работы функции БС его нужно указывать с минусом. Теперь выделяем ячейку B1, растягиваем ее содержимое на ячейки ниже, до B24. Получаем суммарное количество денег на счете в каждом месяце, через 24 месяца получим 58 644 рубля.
Как рассчитать онлайн?
Онлайн расчет процентов можно осуществлять на сайте банка, выбранного для размещения депозита. Для этого нужно найти на странице банка онлайн калькулятор вкладов, ввести в него требуемые данные и рассчитать:
- сумму;
- срок;
- дату начала размещения вклада;
- % ставку;
- период капитализации;
- пополнение (если возможно).
Пример расчета
Расчет при ежемесячной капитализации:
Исходные данные:
Сумма вклада – 50 000 руб.;
Годовая ставка — 8%;
Срок вклада – 12 мес.
50 000 х(1+0,08/12)^12= 54 150 руб.
Налоги на доход по вкладам
За 2021 и 2022 годы налог по вкладам не начисляли вовсе. На доход со вкладов, полученный с 1 января 2023 года, начисляется НДФЛ в размере 13%, но – только на доход, превышающий определенный порог. Порог рассчитывается так: берут максимальную ключевую ставку ЦБ РФ за год, после чего умножают ее на 1 000 000 рублей. Например, максимальная ключевая ставка составила 6% – значит, налогом не будет облагаться доход за год в 60 000 рублей. Если ваш доход за год превысил эту сумму – на сумму превышения начисляется 13%. Если вы получили за год 90 000 рублей дохода со вкладов – с 30 000 рублей нужно будет заплатить 13% НДФЛ, то есть 3 900 рублей. Налог рассчитывается автоматически, в 2024 году вам пришлют уведомление за 2023-й год. Это работает как для резидентов, так и для нерезидентов РФ.
Задачи на простые проценты встречаются в школьном курсе алгебры, экономике, банковской сфере и т.д. Без понимания их содержания и знания формул решить задачи часто бывает сложно. Ниже на распространенных примерах будут даны основные задачи и формулы для их решения.
Процентом ( процентом ) от числа А называется одна сотая часть этого числа. Слово «процент» произошло от латинского pro centо, что значит «с сотни ». Обозначение процентов «%» происходит от искажения письменного сto.
Например: 10% = 0,1; 10 часть числа А.
В случае кредитов и депозитов используют формулы для вычисления простых процентов на период в годах, месяцах и днях. Задачи не требуют сложных вычислений и понравятся как школьникам, так и тем, кто первый раз знакомится с процентами. На практике проценты используют в банковской сфере, химии, медицине, хозяйстве.
Другая часть задач касается нахождения содержания чего-то по известным процентами, или наоборот — за содержанием найти процентное соотношение.
Оба типа задач будут рассмотрены ниже.
Простой процент на период в годах
Формула простого процента на период в годах
P[i]=P*(1+n/100*r) 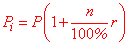
Задача 1. Вкладчик разместил сумму размером 2400 рублей в банк. Определите, какую сумму получит вкладчик через 3 года, если процентная ставка составляет 19 % в год.
Решение: Данные задачи подставляем в формулу простых процентов
P[3]=2400*(1+19/100*3)=3768 (рублей.)
Таким образом за 3 года вкладчик получит 3768 рублей.
Обратная задача на проценты
Обратной задачей на проценты называют такую, в которой за неизвестные выступают количество лет или процентная ставка.
Задача 2. Вкладчик взял в кредит 3000 рублей и должен вернуть через пять лет. Найти процентную ставку кредита, если известно, что нужно отдать банку 8100 грн.
Решение: Выведем формулу для этой задачи.
P[i]=P*(1+n/100*r);
P[i]/P=1+n/100*r;
n= (P[i]/P-1)/r*100.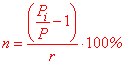
n= (8100/3000-1)/5*100=1,7/5*100=34 (%).
Следовательно, процентная ставка кредита составляет 34 %.
Если в обратной задачи на проценты нужно найти количество лет, то нужная формула на основе предыдущих выкладок будет выглядеть
r= (P[i]/P-1)/n*100
Расчет простых процентов за период в несколько месяцев
Формула простых процентов в этом случае будет иметь вид
P[i]=P*(1+n/100*m/12)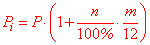
Задача 3. Вкладчик разместил сумму размером 1600 рублей в банк на один год, однако ему пришлось забрать деньги через семь месяцев. Процентная ставка при досрочном снятии депозита составляет 9 % в год. Найти сумму, которую получит вкладчик.
Решение: Применяем формулу для вычислений
P[3]=1600*(1+9/100*7/12)=1684 (рублей.)
За 7 месяцев вкладчик получит 1684 рублей.
Из приведенной формулы достаточно просто получить все необходимые величины для обратной задачи.
Количество месяцев определяют по формуле
m= (P[i]/P-1)/n*100*12
а процентную ставку находят из зависимости
n= (P[i]/P-1)/m*100*12
Расчет простых процентов за период в днях
Данный тип задач применяют при имитации кратковременных кредитов или депозитов. Формула начислений имеет вид
P[i]=P*(1+n/100*d/365)
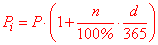
здесь d – количество дней.
Задача 4. Заемщик получил кредит на сумму 20000 рублей под 32% годовых. Через 240 дней кредит был полностью погашен. Рассчитайте, какую сумму заемщик отдал банку? Насколько отличается эта сумма от одолженной?
Решение: Применяем формулу простых процентов для вычислений
P[i]=20000*(1+32/100*240/365)=24208,22 (рублей)
24208,22-20000=4208,22 (рублей)
Получили, что за этот период насчитана сума 4208,22 рублей.
Простые проценты в математике
Задача 5. В класс закупили 3 энергосберегающие окна, которые на 20 % дороже обычных. Сколько потратили денег, если за обычные окна нужно заплатить 1400 гривен.
Решение: Найдем цену энергосберегающего окна
P[в]=1400*(1+20/100)=1680 (грн.)
За три окна заплатили
1680*3=5040 (грн).
Задача 6. В бочке объемом 200 литров перевозили масло . На станции отлили 60 литров. Сколько процентов от обьема осталось?
Решение: Задача состоит в нахождении количества в процентах масла от общего объема бочки.
200-60=140 (л);
140/200*100%=70 %
Осталось 70% объема бочки.
Задача 7. При несвоевременной уплате долгов насчитывают 2% пени за каждый просроченный день. Какую сумму нужно заплатить через 12 дней после срока погашения 500 рублей долга?
Решение: По формуле простых процентов находим
P[i]=500*(1+2/100*12)=620 (рублей)
Нужно заплатить 620 рублей.
Рассмотрим задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир « Аглгебра ». (Номер в скобках)
Задача 8. (542) К сплаву массой 600 г, содержащему 12 % серебра, добавили 60 г серебра. Какое содержание серебра в новом сплаве?
Решение: Определяем сколько грамм серебра в первом сплаве
P[i]=600*12/100=72 (г)
К найденному значению добавляем 60 грамм серебра
P1=72+60=132 (г)
При определении процентного содержания серебра не следует забывать, что вес нового сплава вырос на массу серебра, которую добавили.
Если би Вы вычисляли следующим образом
132/600*100%=22%
то получили — неправильный результат .
ЗАПОМНИТЕ: в подобных задачах сначала находят меру ( вес, объем, длину) нового объекта, а затем находят содержание.
В заданной задачи новый сплав получит массу
P2=600+60=660 (г)
а процентное содержание серебра
P1/P2*100%=132/660*100%=20 %
будет следующим — 20%.
Задача 9. (543) В саду росли яблони и вишни, причем яблони составляли 42% всех деревьев. Вишен было на 48 деревьев больше, чем яблонь. Сколько деревьев росло в саду?
Решение: К правильному ответу можно идти несколькими способами. Рассмотрим следующий из них.
Пусть яблони составляют 42% всех деревьев, тогда вишни
100-42=58%.
Вишен на 48 больше нежели яблонь.
Разница между ними в процентах составляет
58-42=16%
а в количестве — 48 деревьев.
Задача состоит в нахождении количества деревьев, поэтому складываем отношения
16% – 48 деревьев
100 % –Х деревьев
Отсюда находим количество деревьев в саду
Х=100*48/16=300 (деревьев).
Задача 10. (544) За два дня был проложен кабель. За первый день проложили 56% кабеля, а за другой — на 132 м меньше, чем первого. Сколько всего метров кабеля было проложено за два дня?
Решение: Задача похожа на предыдущую. За второй день проложили
100-56=44%
кабеля, разница между первым и вторым днем составляет
56-44=12%
и составляет 132 метра.
На основе этого составляем отношение
12% – 132 м
100 % –Х м
Отсюда находим искомую длину
Х=100*132/12=1100 (м.)
За два дня проложили 1100 м.. кабеля.
Задача 11. (545) За первый день мальчик прочитал 25% всей книги, за второй — 72% от количества страниц что осталась, а за третий — остальные 84 страницы. Сколько страниц в книге?
Решение: 72 % процента от остатка книги составляет
72*(100-25)/100= 54%.
На третий день оставалось прочитать
100-25-54=21%
или 84 страницы.
Составляем соотношение
21% – 84 ст
100 % –Х ст
с которого находим
Х=100*84/21=400 (ст),
что книга содержит 400 страниц.
Сложные задачи на простые проценты
В данную категорию входят задачи , которые вызывают немало трудностей у школьников. Однако , если достаточно хорошо разобраться в их решении, то все сложности отходят на второй план.
Задача 12. (547) Морская вода содержит 5% соли. Сколько пресной воды нужно добавить к 40 кг морской воды, чтобы концентрация соли составляла 2% ?
Решение: Находим вес соли в 40 кг морской воды
40*5/100=2 (кг).
Находим вес воды, которая содержала 2% соли (2 кг)
2% – 2 кг
100 % –Х кг
или
Х=100*2/2=100 кг.
Сейчас у нас есть 40 кг воды, поэтому нужно добавить
100-40=60 кг
пресной воды.
Задача 13. (554) Перемешали 30- процентный раствор соляной кислоты с 10- процентным раствором и получили 800 г 15 — процентного раствора. Сколько граммов каждого раствора взяли для этого?
Решение: В таких задачах требуется составить два уравнения, решение которых и приведет к отысканию нужных величин.
Обозначим A – вес первого раствора, B – соответственно второго.
Тогда из условия задачи составляем два уравнения:
первый касается процентных соотношений ( * 100 )
30*A+10*B=800*15
второе — веса смеси
A+B=800.
С второго выражаем одну из неизвестных и подставляем в первое уравнение
A=800-B;
30*(800-B)+10*B=800*15
и решаем его
24000-30*B+10*B=12000;
20*B=24000-12000=12000;
B=12000/20=600 (г).
Массу первого раствора находим из зависимости
A=800-B=800-600=200 (г).
Следовательно, нужно 600 г 30% раствора и 200 г 10% раствора соляной кислоты.
Задача 14. (560) К сплаву меди и цинка, содержащему меди на 12 кг больше, чем цинка, добавили 6 кг меди. Вследствие этого содержание цинка в сплаве снизилось на 5%. Сколько цинка и сколько меди содержал сплав в самом начале?

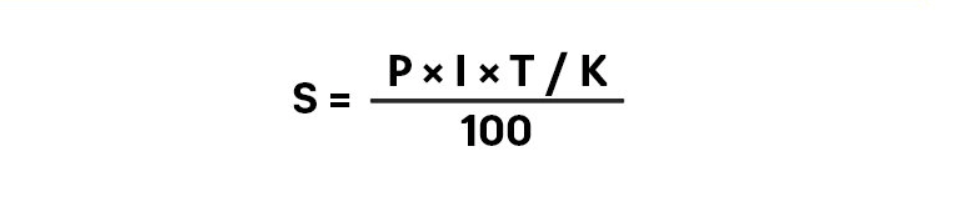


/formula-rascheta-procentov-po-vkladam-2.jpg)

/formula-rascheta-procentov-po-vkladam-4.jpg)