Как найти радиус окружности вращения электрона
Определите радиус окружности и период обращения электрона. Физика, 11 класс, параграф 1-7, 4 задача. Мякишев и Буховцев
Всем привет. Решили уже?
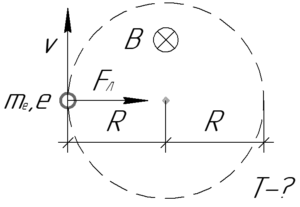
Определите радиус окружности и период обращения электрона в однородном магнитном поле с индукцией B =0,01 Тл. Скорость электрона перпендикулярна вектору магнитной индукции и равна 106 м/с.
Привет! Вот
Сила Лоренца является центростремительной силой:
Период обращения:
Ответ: 0,57 мм; 3,6 нс.
Шпаргалка по общей электронике и электротехнике.
5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
В некоторых электровакуумных приборах используется движение электронов в магнитном поле.
Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.
При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.
Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.
Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.
Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).
Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.
Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.
Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.
Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.
Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.
Сила Лоренца
Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Величина и направление силы Лоренца определяются соотношением
где $vector $, $vector $ и $vector $ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Вычислить, найти силу Лоренца действующую на электрон или протон
Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10 -31 кг — масса электрона, | кг |
| e | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
При больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя электронов me, а необходимо учитывать релятивистское увеличение массы.
Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Радиус траектории протона в магнитном поле
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10 -27 кг — масса протона, | кг |
| p | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Аналогично при больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя протонов mp, а необходимо учитывать релятивистское увеличение массы.
Определите радиус окружности и период обращения электрона. Физика, 11 класс, параграф 1-7, 4 задача. Мякишев и Буховцев
Всем привет. Решили уже?
Определите радиус окружности и период обращения электрона в однородном магнитном поле с индукцией B =0,01 Тл. Скорость электрона перпендикулярна вектору магнитной индукции и равна 106 м/с.
Привет! Вот
Сила Лоренца является центростремительной силой:
Период обращения:
Ответ: 0,57 мм; 3,6 нс.
№ 842. Электрон движется в однородном магнитном поле индукцией В = 4 мТл. Найти период Т обращения электрона.

задача №842
к главе «ГЛАВА IX. МАГНИТНОЕ ПОЛЕ. 39. Магнитное поле тока. Магнитная индукция. Магнитный поток. Закон Ампера. Сила Лоренца. Магнитные свойства веществ».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
http://class.rambler.ru/temy-gdz/opredelite-radius-okruzhnosti-i-period-obrascheniya-elektrona-fizika-11-klass-paragraf-1-7-4-zadacha-myakishev-i-buhovcev-14553.htm
http://5terka.com/node/3991
При
движении в магнитном поле на электрон
действует сила Лоренца (рис.3.1):
,
(3.1)
где
-е — заряд электрона (e > 0), v
— скорость электрона, B
— индукция магнитного поля.
Таким
образом, Fл
= -еvB
sin,
где
— угол между векторами
и
,
а направлениевыбирается так, как показано на рис.3.1
(вспомните определение векторного
произведения).
|
Рис.3.1 |
Если
|
откуда
радиус окружности, по которой движется
электрон, равен
, (3.3)
Один
оборот электрон совершает за время
, (3.4)
Таким
образом, период обращения электрона по
окружности не зависит от скорости
электрона. Период определяется только
величиной индукции
и удельным зарядом электрона.
Если
угол
между векторами скорости
и индукции
не равен,
то скорость
можно представить в виде суммы:
,
где,
а.
При этом,
так как.
Таким
образом, электрон движется с постоянной
скоростью
вдоль
и одновременно вращается вокруг
линии, параллельной,
с периодом,
|
Рис.3.2 |
определенным |
Предположим,
что в однородном магнитном поле В из
некоторой точки С вылетают электроны
(пучок электронов), имеющие одинаковую
скорость
и разные скорости
.
Если«
для всех электронов (малые углы α,
см.рис.3.3), то.
В этом случае все электроны, вылетающие
из точки С, через одинаковое время Т
попадут в одну и ту же точку О или, как
говорят, сфокусируются в точке О.
Очевидно, что
Следовательно,
зная расстояние СО, v
и В, можно найти е/m.
На этой идее и основан метод определения
удельного заряда электрона в дан- ной
работе. На рис.3.3 схематически показана
электронно-лучевая трубка. Электроны,
испускаемые горячим катодом, проходят
через отверстие в диафрагме А, играющей
роль анода.
|
|
При ½mv2
Затем |
ется
переменное напряжение. Под действием
переменного электрического поля
электроны в разные моменты времени
будут отклоняться на разные углы α от
оси прибора и на экране трубки появится
светящаяся полоска НК (см. рис.3.3).
Кроме
электрического поля на электрон будет
действовать продольное магнитное поле
соленоида, внутрь которого вставлена
электронно-лучевая трубка. Таким образом,
в промежутке между диафрагмой и экраном
электроны будут двигаться по винтовым
линиям.
При
увеличении магнитного поля линия НК на
экране осциллографа сокращается и
постепенно стягивается в точку. Эту
точку называют фокусом
электронов.
Обозначим через Вф
магнитное поле, при котором наступает
фокусировка. За время Т
электроны проходят отрезок
L
= v||Т. (3.6)
Учитывая,
что v||
≈
v
при малых α выражение (3.4) в формулу (3.6)
получим:
(3.7)
Таким
образом, все электроны через время,
равное одному периоду, пересекут ось
прибора на одинаковом расстоянии L от
конденсатора. На рис.3.3 показаны траектории
нескольких электронов. Все они пересекаются
в одной точке О.
Магнитное
поле можно подобрать так, чтобы фокус
пришелся как раз на флуоресцирующий
экран. При этом отрезок L равен расстоянию
между конденсатором и экраном, которое
легко измерить.
Подставляя
в формулу (3.7) значение скорости из
выражения (3.5), получаем расчетную формулу
для удельного заряда электрона:
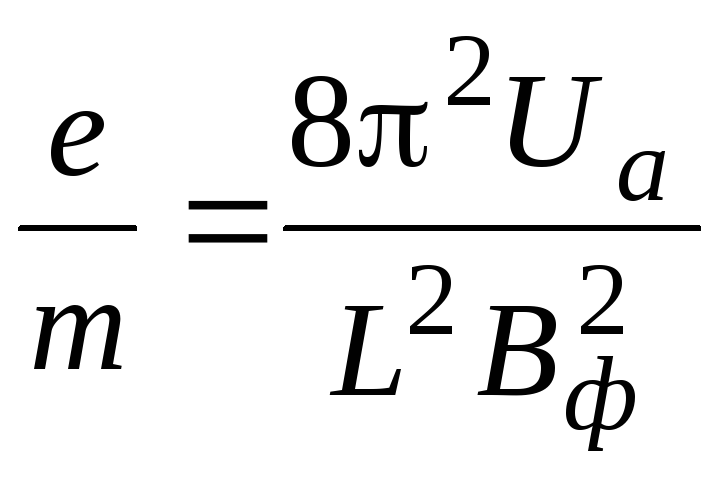
В
данной установке используется электронный
осциллограф СИ-1, электронно-лучевая
трубка которого вынута из него и
закреплена в соленоиде, создающем
магнитное поле. Оси трубки и соленоида
совпадают. Питание трубки и напряжение,
подаваемое на отклоняющие пластины,
подводятся многожильным кабелем. Анодное
напряжение трубки измеряется
электростатическим киловольтметром.
-
Порядок
выполнения работы
-
Собрать
схему (имеется на рабочем месте установки.
При этом ручки осциллографа установить
в положение: «Род синхронизации»
— на «Внешнее, «Делитель» — на
«Калибровку», «Род работы» —
на «Усиление». -
Включить
блок питания осциллографа. После
прогрева на экране трубки должна
появиться светящаяся линия. Отрегулировать
яркость и четкость линии ручками
«Яркость» и «Фокус». Расположить
светящуюся линию в центре экрана
электронно-лучевой трубки ручками
«Смещение У» и «Смещение Х». -
С
помощью ручек осциллографа «Усиление»
и «Калибровка» ограничить длину
светящейся линии до 1..1,5 см, чтобы угол
α был мал. -
Измерить
величину ускоряющего напряжения Ua
с помощью вольтметра блока питания.
Величину Ua
записать в таблицу измерения. -
Включить
блок питания соленоида тумблером
«Сеть». Перед включением ручка
«Регулировка тока соленоида»
должна находиться в положении «О». -
Постепенно
увеличивая силу тока в соленоиде,
добиться, чтобы светящаяся линия на
экране трубки стянулась в точку при
данной величине ускоряющего потенциала.
При дальнейшем увеличении силы тока
на экране вновь появится светящаяся
линия, которая затем снова стянется в
точку. Второе прохождение через фокус
происходит в том случае, когда электроны
на пути к экрану совершают два оборота
по винтовой линии, третье прохождение
— при трех оборотах и т.д. Каждое
прохождение электронов фиксируется и
значение тока соленоида Iсn
/
n
(n
— число прохождения электронов через
фокус), соответствующее этим прохождениям,
заносится в таблицу измерений. -
На
движение электронов в трубке влияют
внешние поля. Наибольшее влияние на
точность измерений оказывает продольное
магнитное поле, складывающееся с полем
соленоида. Внешнее продольное поле
накладывается на поле соленоида. Для
того, чтобы исключить влияние внешних
полей, измерения, указанные в п.6
проводятся при двух направлениях тока
в соленоиде. Это выполняется с помощью
тумблера «Переполюсовка соленоида».
Полученные
значения I+сn
при прямом включении соленоида и I—cn
при обратном включении соленоида нужно
усреднить для каждого прохождения
электронов через фокус и среднее значение
занести в таблицу измерений. Соответствующие
значения Вфп
найти по графику В= f(I).
Если
Вф1,
Вф2,
Вф3
— магнитные поля, при которых электроны
фокусируются на экране после прохождения
одного, двух и трех витков по спирали
соответственно, то нужно найти среднее
значение
,
которое
и подставляется затем в формулу (3.8) для
определения е/m.
Абсолютная
ошибка в определении e/m находится по
формуле
где
учтено, что ∆Вф/Вф
= ∆Iс/Iс.
Таблица
2
|
m |
I+сn, |
I—cn, |
Icn, |
Вфп, |
Ua, |
L, |
e/m, |
∆(e/m), |
|
1 |
||||||||
|
2 |
||||||||
|
3 |
-
Контрольные
вопросы
-
Сила
Лоренца. -
По
какой траектории движется электрон в
однородном магнитном поле при произвольном
направлении начальной скорости? -
В
чем заключается фокусировка электронов? -
Каким
будет движение электронов в
электронно-лучевой трубке при переменном
напряжении на отклоняющих пластинах
при В = О и В ≠ О? -
Как
изменяется скорость электронов при
движении в постоянном магнитном поле? -
Чему
равен период обращения электрона в
магнитном поле? -
Получите
расчетная формула для определения е/m.
Литература.
[1, §§ 18.1, 18.3; 2, §§ 36-38; 3, §§ 41, 43] .
-
ОПРЕДЕЛЕНИЕ
УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
МЕТОДОМ
МАГНЕТРОНА
Цель
работы:
знакомство с методом магнетрона и
определение удельного заряда электрона
(е/m).
Приборы
и принадлежности:
электронная лампа 2Ц2С (или аналогичная
ей), соленоид, источник питания, вольтметр,
амперметр, миллиамперметр.
Лучший ответ
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
№ 842. Электрон движется в однородном магнитном поле индукцией В = 4 мТл. Найти период Т обращения электрона.

задача №842
к главе «ГЛАВА IX. МАГНИТНОЕ ПОЛЕ. 39. Магнитное поле тока. Магнитная индукция. Магнитный поток. Закон Ампера. Сила Лоренца. Магнитные свойства веществ».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
Как найти период обращения электрона
Атом Бора. Рентгеновские лучи
Найти период Т обращения электрона на первой боровской орбите атома водорода и его угловую скорость ω.
Дано:
Решение:
Внутренняя энергия атома равна сумме кинетической и потенциальной энергии
По II – му постулату Бора
Период обращения электрона на первой боровской орбите атома водорода
Или проще, если известны скорость и радиус на первой боровской орбите (см. задачу 20.1),
Электрон влетает в однородное магнитное поле с индукцией 0,004 Тл так, что направление
Электрон влетает в однородное магнитное поле с индукцией 0,004 Тл так, что направление его скорости перпендикулярно линиям магнитной индукции. Найти период обращения электрона.
Задача №8.2.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
Под действием силы Лоренца электрон в магнитном поле будет совершать равномерное движение по окружности. Очевидно, что если электрон движется по окружности радиуса (R) со скоростью (upsilon), то период обращения (T), то есть время, за которое электрон сделает один оборот (одну длину окружности, равную (2pi R)), можно найти так:
Силу Лоренца (F_Л) определяют по следующей формуле:
Здесь (B) – индукция магнитного поля, (upsilon) – скорость электрона, (e) – модуль заряда электрона, (alpha) – угол между вектором скорости и вектором магнитной индукции.
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.
Сила Лоренца (F_Л) сообщает электрону центростремительное ускорение (a_ц), поэтому из второго закона Ньютона следует, что:
Центростремительное ускорение (a_ц) можно определить через скорость (upsilon) и радиус кривизны траектории (R) по формуле:
Подставим (4) в (3), тогда:
Приравняем правые части (2) и (5):
Откуда отношение (frac), которое нам будет нужно в ходе дальнейшего решения, равно:
Полученное выражение подставим в (1):
Напомним, что масса электрона (m_e) равна 9,1·10 -31 кг, а его заряд (e) (вернее модуль заряда) равен 1,6·10 -19 Кл. Подставим численные данные в формулу и посчитаем ответ:
Ответ: 8,9 нс.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.

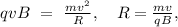
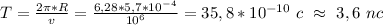
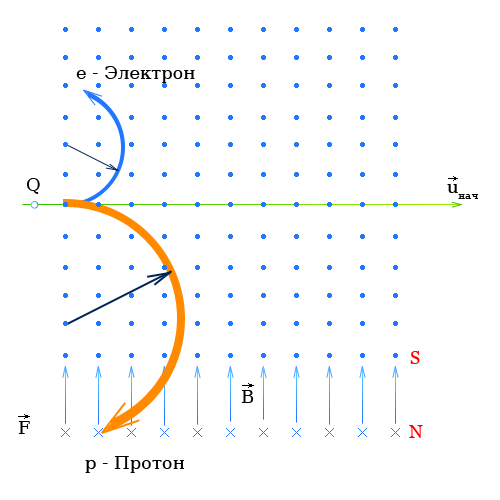
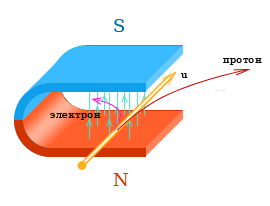

 Рис.3.3
Рис.3.3