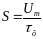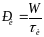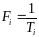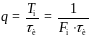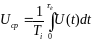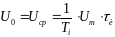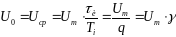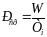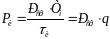Частота повторения импульсов
время передачи
или длительность
импульса τ
Следующий
зондирующий
импульс
Тестовые
импульсы
Эхо-сигнал
интервал приема
интервал
покоя
Время повторения импульса (PRT)
или период повторения импульса (PRP)
Рис. 1: Временные этапы периодов работы радиолокатора
время передачи
или длительность
импульса τ
Следующий
зондирующий
импульс
Тестовые
импульсы
Эхо-сигнал
интервал приема
интервал
покоя
Время повторения импульса (PRT)
или период повторения импульса (PRP)
Рис. 1: Временные этапы периодов работы радиолокатора
Что такое частота повторения?
Частота повторения импульсов
Частота повторения импульсов (англ.: Pulse Repetition Frequency PRF )
— это количество импульсов, которые формируются передатчиком в единицу времени, обычно — в секунду.
Радиолокатор излучает каждый импульс на несущей частоте в течение времени передачи (или длительности импульса τ),
ожидает возврата эхо-сигналов в течение времени «слушания» или интервала приема и затем излучает следующий импульс (что показано на Рисунке 1).
Время между началом одного импульса и началом следующего импульса называется периодом повторения (иногда — следования) импульсов или межимпульсным интервалом
(англ.: Pulse Repetition Time PRT
или Pulse Repetition Period PRP ).
Период повторения импульсов есть величина, обратная частоте повторения импульсов, то есть:
Интервал приема
В общем смысле, интервал приема — это интервал времени между излучаемыми импульсами.
Интервал приема всегда меньше чем разность между периодом повторения импульсов и длительностью импульса.
Он иногда ограничивается так называемым интервалом покоя,
в течение которого приемник уже выключен непосредственно перед следующим излучаемым импульсом.
В некоторых радиолокаторах между излучаемым импульсом и интервалом приема существует короткий интервал времени,
соответствующий времени восстановления антенного переключателя.
В течение этого времени
антенный переключатель
исключает проникновение излучаемых импульсов большой мощности в приемник.
В случае очень низкой излучаемой мощности необходимости в этом нет и прием эхо-сигналов может происходить уже во время излучения.
В таких случаях интервал приема включает в себя время излучения.
следующая пачка
пачка
(состоящая здесь из
четырех импульсов)
общий интервал покоя
Рисунок 2. Режим излучения пачек для импульсного радиолокатора
следующая пачка
пачка
(состоящая здесь из
четырех импульсов)
общий интервал покоя
Рисунок 2. Режим излучения пачек для импульсного радиолокатора
Интервал покоя
Если интервал приема заканчивается еще до момента излучения следующего импульса, то промежуток между ними называют интервалом покоя.
Как правило, в современных радиолокаторах в этом промежутке времени выполняются циклы тестирования.
Для радиолокаторов, использующих
фазированные антенные решетки,
такой интервал покоя является критически необходимым.
В это время
фазовращатели
антенны должны быть перепрограммированы для подготовки к переносу луча антенны в следующее требуемое направление.
Эта операция может занимать до 200 мкс, поэтому в таких случаях интервал покоя принимает довольно большие значения по сравнению с интервалом приема.
В течение этого интервала покоя приемник уже выключен поскольку во время перепрограммирования антенны не может выполняться прием эхо-сигналов.
Поскольку в течение интервала покоя в любом случае не могут быть обработаны никакие реальные данные,
то это время используется для выполнения внутренних процедур тестирования в модулях приемного тракта.
Это делается для проверки состояния определенных электронных цепей и, в случае необходимости, их регулировки.
Для этого генерируются сигналы с известными параметрами.
Такие сигналы поступают в приемный тракт и их обработка в отдельных модулях контролируется.
Для того, чтобы отметки этих сигналов не появлялись на индикаторе видеопроцессор отключает эти сигналы.
При необходимости, по результатам тестирования модули приемника могут быть автоматически перенастроены и сформировано детализированное сообщение об ошибке.
Режим излучения пачек импульсов
Распределение длительности интервала покоя не должно быть равномерным.
Для этого могут излучаться один за другим несколько импульсов, каждый из которых имеет короткий интервал приема до начала интервала покоя.
Например, если в течение нескольких периодов импульсы излучаются в одном направлении
(как это необходимо для обработки пары импульсов или для
обнаружения движущейся цели), тогда интервал покоя не является необходимым.
Это положительно влияет на
бюджет времени радиолокатора.
Кроме этого, в течение более короткого времени случайное нежелательное изменение фазы генерируемого сигнала маловероятно.
Поэтому радиолокатор будет более точным при измерении дальности.
Одновременно с этим в таком режиме частота повторения импульсов намного выше, чем в обычном режиме.
Благодаря этому увеличивается однозначно определяемая скорость (смотри
Противоречие Допплера).
Режим излучения пачек импульсов в основном используется в
дидактических (учебных) радиолокаторах.
В таких радиолокаторах не требуется большого интервала приема из-за коротких расстояний в лабораторных помещениях.
Однако им требуется более длительный интервал покоя для передачи данных об эхо-сигналах по относительно узкополосному последовательному интерфейсу на компьютер.
Например, они передают только 10 импульсов в секунду, что соответствует средней частоте повторения импульсов 10 Гц.
Эти десять импульсов передаются, но в течение 200 микросекунд.
Для расчета однозначной допплеровской частоты это соответствует частоте повторения импульсов 50 кГц.
Последующее время покоя составляет почти целую секунду.
В течение этого времени данные передаются по интерфейсу USB со скоростью 280 Мбит/с.
The pulse repetition frequency (PRF) is the number of pulses of a repeating signal in a specific time unit. The term is used within a number of technical disciplines, notably radar.
In radar, a radio signal of a particular carrier frequency is turned on and off; the term «frequency» refers to the carrier, while the PRF refers to the number of switches. Both are measured in terms of cycle per second, or hertz. The PRF is normally much lower than the frequency. For instance, a typical World War II radar like the Type 7 GCI radar had a basic carrier frequency of 209 MHz (209 million cycles per second) and a PRF of 300 or 500 pulses per second. A related measure is the pulse width, the amount of time the transmitter is turned on during each pulse.
After producing a brief pulse of radio signal, the transmitter is turned off in order for the receiver units to hear the reflections of that signal off distant targets. Since the radio signal has to travel out to the target and back again, the required inter-pulse quiet period is a function of the radar’s desired range. Longer periods are required for longer range signals, requiring lower PRFs. Conversely, higher PRFs produce shorter maximum ranges, but broadcast more pulses, and thus radio energy, in a given time. This creates stronger reflections that make detection easier. Radar systems must balance these two competing requirements.
Using older electronics, PRFs were generally fixed to a specific value, or might be switched among a limited set of possible values. This gives each radar system a characteristic PRF, which can be used in electronic warfare to identify the type or class of a particular platform such as a ship or aircraft, or in some cases, a particular unit. Radar warning receivers in aircraft include a library of common PRFs which can identify not only the type of radar, but in some cases the mode of operation. This allowed pilots to be warned when an SA-2 SAM battery had «locked on», for instance. Modern radar systems are generally able to smoothly change their PRF, pulse width and carrier frequency, making identification much more difficult.
Sonar and lidar systems also have PRFs, as does any pulsed system. In the case of sonar, the term pulse repetition rate (PRR) is more common, although it refers to the same concept.
Introduction[edit]
Electromagnetic (e.g. radio or light) waves are conceptually pure single frequency phenomena while pulses may be mathematically thought of as composed of a number of pure frequencies that sum and nullify in interactions that create a pulse train of the specific amplitudes, PRRs, base frequencies, phase characteristics, et cetera (See Fourier Analysis). The first term (PRF) is more common in device technical literature (Electrical Engineering and some sciences), and the latter (PRR) more commonly used in military-aerospace terminology (especially United States armed forces terminologies) and equipment specifications such as training and technical manuals for radar and sonar systems.
The reciprocal of PRF (or PRR) is called the pulse repetition time (PRT), pulse repetition interval (PRI), or inter-pulse period (IPP), which is the elapsed time from the beginning of one pulse to the beginning of the next pulse. The IPP term is normally used when referring to the quantity of PRT periods to be processed digitally. Each PRT having a fixed number of range gates, but not all of them being used. For example, the APY-1 radar used 128 IPP’s with a fixed 50 range gates, producing 128 Doppler filters using an FFT. The different number of range gates on each of the five PRF’s all being less than 50.
Within radar technology PRF is important since it determines the maximum target range (Rmax) and maximum Doppler velocity (Vmax) that can be accurately determined by the radar.[1] Conversely, a high PRR/PRF can enhance target discrimination of nearer objects, such as a periscope or fast moving missile. This leads to use of low PRRs for search radar, and very high PRFs for fire control radars. Many dual-purpose and navigation radars—especially naval designs with variable PRRs—allow a skilled operator to adjust PRR to enhance and clarify the radar picture—for example in bad sea states where wave action generates false returns, and in general for less clutter, or perhaps a better return signal off a prominent landscape feature (e.g., a cliff).
Definition[edit]
Pulse repetition frequency (PRF) is the number of times a pulsed activity occurs every second.
This is similar to cycle per second used to describe other types of waveforms.
PRF is inversely proportional to time period 
PRF is usually associated with pulse spacing, which is the distance that the pulse travels before the next pulse occurs.
Physics[edit]
PRF is crucial to perform measurements for certain physics phenomenon.
For example, a tachometer may use a strobe light with an adjustable PRF to measure rotational velocity. The PRF for the strobe light is adjusted upward from a low value until the rotating object appears to stand still. The PRF of the tachometer would then match the speed of the rotating object.
Other types of measurements involve distance using the delay time for reflected echo pulses from light, microwaves, and sound transmissions.
Measurement[edit]
PRF is crucial for systems and devices that measure distance.
- Radar
- Laser range finder
- Sonar
Different PRF allow systems to perform very different functions.
A radar system uses a radio frequency electromagnetic signal reflected from a target to determine information about that target.
PRF is required for radar operation. This is the rate at which transmitter pulses are sent into air or space.
Range ambiguity[edit]
A real target in 100 km or a second-sweep echo in a distance of 400 km
A radar system determines range through the time delay between pulse transmission and reception by the relation:
For accurate range determination a pulse must be transmitted and reflected before the next pulse is transmitted. This gives rise to the maximum unambiguous range limit:
The maximum range also defines a range ambiguity for all detected targets. Because of the periodic nature of pulsed radar systems, it is impossible for some radar system to determine the difference between targets separated by integer multiples of the maximum range using a single PRF. More sophisticated radar systems avoid this problem through the use of multiple PRFs either simultaneously on different frequencies or on a single frequency with a changing PRT.
The range ambiguity resolution process is used to identify true range when PRF is above this limit.
Low PRF[edit]
Systems using PRF below 3 kHz are considered low PRF because direct range can be measured to a distance of at least 50 km. Radar systems using low PRF typically produce unambiguous range.
Unambiguous Doppler processing becomes an increasing challenge due to coherency limitations as PRF falls below 3 kHz.
For example, an L-Band radar with 500 Hz pulse rate produces ambiguous velocity above 75 m/s (170 mile/hour), while detecting true range up to 300 km. This combination is appropriate for civilian aircraft radar and weather radar.
Low PRF radar have reduced sensitivity in the presence of low-velocity clutter that interfere with aircraft detection near terrain. Moving target indicator is generally required for acceptable performance near terrain, but this introduces radar scalloping issues that complicate the receiver. Low PRF radar intended for aircraft and spacecraft detection are heavily degraded by weather phenomenon, which cannot be compensated using moving target indicator.
Medium PRF[edit]
Range and velocity can both be identified using medium PRF, but neither one can be identified directly. Medium PRF is from 3 kHz to 30 kHz, which corresponds with radar range from 5 km to 50 km. This is the ambiguous range, which is much smaller than the maximum range. Range ambiguity resolution is used to determine true range in medium PRF radar.
Medium PRF is used with Pulse-Doppler radar, which is required for look-down/shoot-down capability in military systems. Doppler radar return is generally not ambiguous until velocity exceeds the speed of sound.
A technique called ambiguity resolution is required to identify true range and speed. Doppler signals fall between 1.5 kHz, and 15 kHz, which is audible, so audio signals from medium-PRF radar systems can be used for passive target classification.
For example, an L band radar system using a PRF of 10 kHz with a duty cycle of 3.3% can identify true range to a distance of 450 km (30 * C / 10,000 km/s). This is the instrumented range. Unambiguous velocity is 1,500 m/s (3,300 mile/hour).
The unambiguous velocity of an L-Band radar using a PRF of 10 kHz would be 1,500 m/s (3,300 mile/hour) (10,000 x C / (2 x 10^9)). True velocity can be found for objects moving under 45,000 m/s if the band pass filter admits the signal (1,500/0.033).
Medium PRF has unique radar scalloping issues that require redundant detection schemes.
High PRF[edit]
Systems using PRF above 30 kHz function better known as interrupted continuous-wave (ICW) radar because direct velocity can be measured up to 4.5 km/s at L band, but range resolution becomes more difficult.
High PRF is limited to systems that require close-in performance, like proximity fuses and law enforcement radar.
For example, if 30 samples are taken during the quiescent phase between transmit pulses using a 30 kHz PRF, then true range can be determined to a maximum of 150 km using 1 microsecond samples (30 x C / 30,000 km/s). Reflectors beyond this range might be detectable, but the true range cannot be identified.
It becomes increasingly difficult to take multiple samples between transmit pulses at these pulse frequencies, so range measurements are limited to short distances.[2]
Sonar[edit]
Sonar systems operate much like radar, except that the medium is liquid or air, and the frequency of the signal is either audio or ultra-sonic. Like radar, lower frequencies propagate relatively higher energies longer distances with less resolving ability. Higher frequencies, which damp out faster, provide increased resolution of nearby objects.
Signals propagate at the speed of sound in the medium (almost always water), and maximum PRF depends upon the size of the object being examined. For example, the speed of sound in water is 1,497 m/s, and the human body is about 0.5 m thick, so the PRF for ultrasound images of the human body should be less than about 2 kHz (1,497/0.5).
As another example, ocean depth is approximately 2 km, so sound takes over a second to return from the sea floor. Sonar is a very slow technology with very low PRF for this reason.
Laser[edit]
Light waves can be used as radar frequencies, in which case the system is known as lidar. This is short for «LIght Detection And Ranging,» similar to the original meaning of the initialism «RADAR,» which was RAdio Detection And Ranging. Both have since become commonly-used english words, and are therefore acronyms rather than initialisms.
Laser range or other light signal frequency range finders operate just like radar at much higher frequencies. Non-laser light detection is utilized extensively in automated machine control systems (e.g. electric eyes controlling a garage door, conveyor sorting gates, etc.), and those that use pulse rate detection and ranging are at heart, the same type of system as a radar—without the bells and whistles of the human interface.
Unlike lower radio signal frequencies, light does not bend around the curve of the earth or reflect off the ionosphere like C-band search radar signals, and so lidar is useful only in line of sight applications like higher frequency radar systems.
See also[edit]
- Radar
- Pulse-Doppler radar
- Weather radar
References[edit]
- ^ «Pulse Repetition Frequency». Radartutorial.
- ^ Piper, Samuel; Wiltse, James (2007). «Continuous Wave Radar». RF and Microwave Applications and Systems. Electrical Engineering Handbook. Vol. 20071745. doi:10.1201/9781420006711.ch14. ISBN 978-0-8493-7219-3. Retrieved January 29, 2011.[permanent dead link]
-
Электрические импульсы и их параметры
Под
электрическим
импульсом
понимают отклонение напряжения или
тока от некоторого постоянного уровня
(в частности, от нулевого), наблюдаемое
в течение времени, меньшего или сравнимого
с длительностью переходных процессов
в схеме.
Как
уже было сказано, под переходным процессом
понимается всякое резкое изменение
установившегося режима в электрической
цепи за счёт действия внешних сигналов
или переключений внутри самой цепи.
Таким образом, переходный процесс –
это процесс перехода электрической
цепи из одного стационарного состояния
в другое. Как бы ни был короток этот
переходный процесс, – он всегда конечен
во времени. Для цепей, в которых время
существования переходного процесса
несравненно меньше времени действия
внешнего сигнала (напряжения или тока),
режим работы считается установившимся,
а сам внешний сигнал для такой цепи не
является импульсным. Примером этого
может служить срабатывание электромагнитного
реле.
Когда
же длительность действующих в электрической
цепи сигналов напряжения или тока
становится соизмеримой с длительностью
процессов установления, переходный
процесс оказывает настолько сильное
влияние на форму и параметры этих
сигналов, что их нельзя не учитывать. В
этом случае бóльшая часть времени
воздействия сигнала на электрическую
цепь совпадает со временем существования
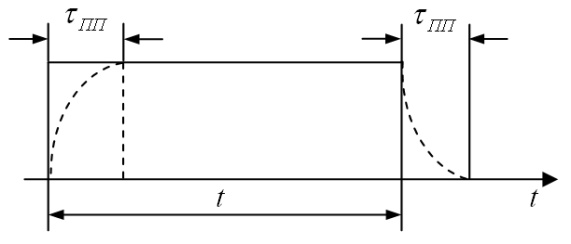
переходного процесса (рис.1.4). Режим
работы цепи во время действия такого
сигнала будет нестационарным, а
воздействие его на электрическую цепь
– импульсным.
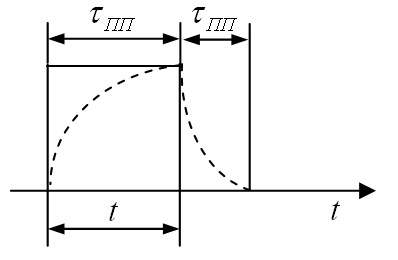
а)
б)
Рис.1.4.
Соотношение между длительностью сигнала
и длительностью
переходного
процесса:
а)
длительность
переходного процесса значительно меньше
длительности
сигнала
(τпп
<<
t);
б)
длительность переходного процесса
соизмерима с длительностью
сигнала
(τпп
≈
t).
Отсюда
следует, что понятие импульса связывается
с параметрами конкретной цепи и что не
для всякой цепи сигнал можно считать
импульсным.
Таким
образом, электрическим
импульсом для данной цепи называется
напряжение или ток, действующие в течение
промежутка времени, соизмеримого с
длительностью переходного процесса в
этой цепи.
При этом
предполагается, что между двумя
последовательно действующими в цепи
импульсами должен быть достаточный
промежуток времени, превышающий
длительность процесса установления. В
противном случае вместо импульсов будут
возникать сигналы сложной формы
(рис.1.5).
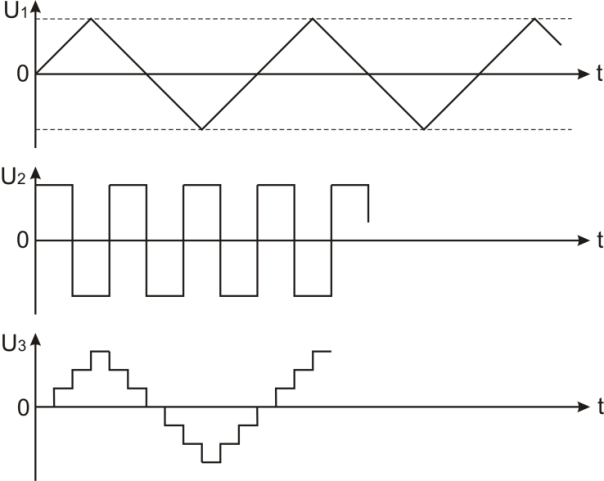
Рис.1.5. Электрические
сигналы сложной формы
Наличие
промежутков времени сообщает импульсному
сигналу характерную прерывистую
структуру. Некоторая условность таких
определений заключается в том, что
процесс установления теоретически
длится бесконечно.
Могут
быть такие промежуточные случаи, когда
переходные процессы в цепях не успевают
практически заканчиваться от импульса
к импульсу, хотя действующие сигналы
продолжают называть импульсными. В
таких случаях возникают дополнительные
искажения формы импульсов, вызванные
наложением переходного процесса на
начало последующего импульса.
Различают
два вида импульсов: видеоимпульсы
и радиоимпульсы.
Видеоимпульсы получают при коммутации
(переключении) цепи постоянного тока.
Такие импульсы не содержат высокочастотных
колебаний и имеют постоянную составляющую
(среднее значение), отличную от нуля.
Видеоимпульсы
принято различать по их форме. На рис.
1.6. показаны наиболее часто встречающиеся
видеоимпульсы.
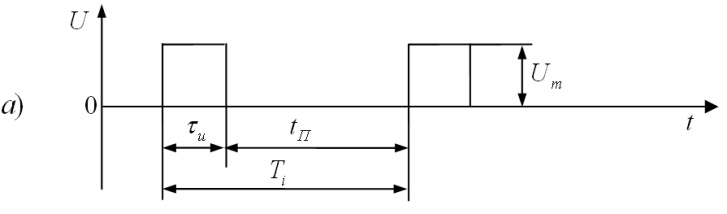
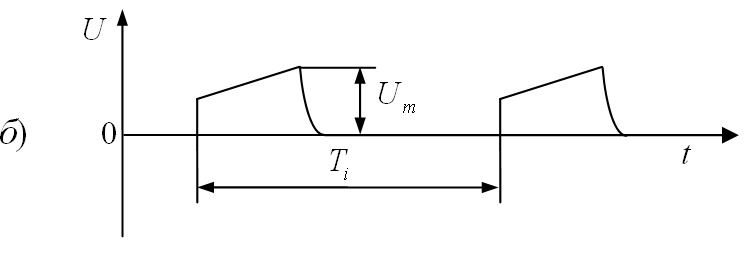
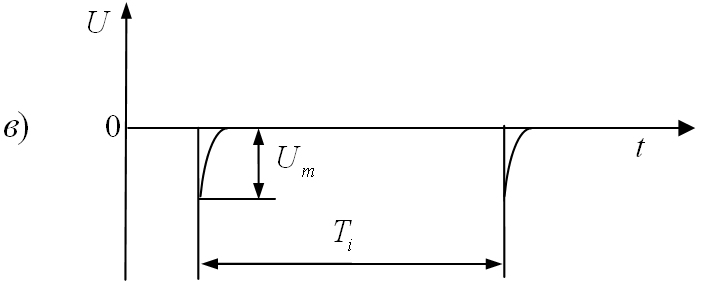
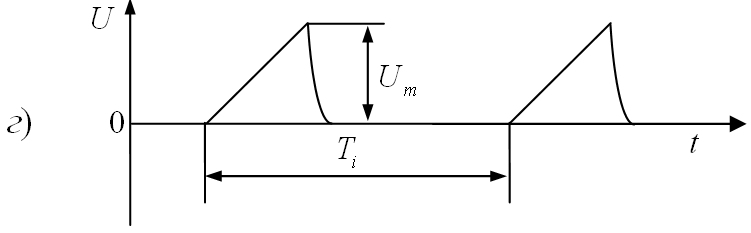
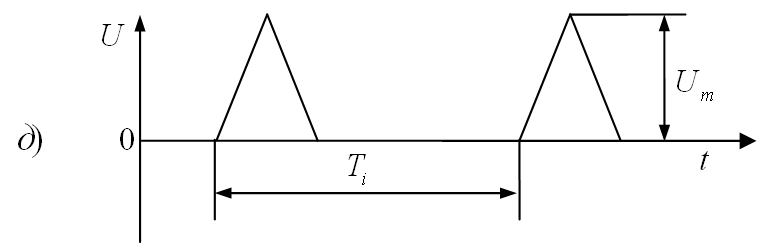
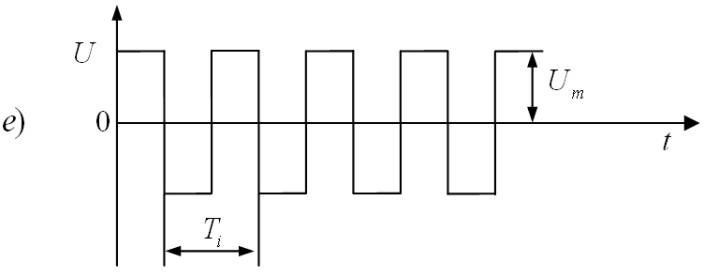
Рис.
1.6. Формы видеоимпульсов:
а)
прямоугольные; б)
трапецеидальные; в)
остроконечные;
г)
пилообразные; д)
треугольные; е)
разнополярные.
Рассмотрим
основные параметры одиночного импульса
(рис.1.7).
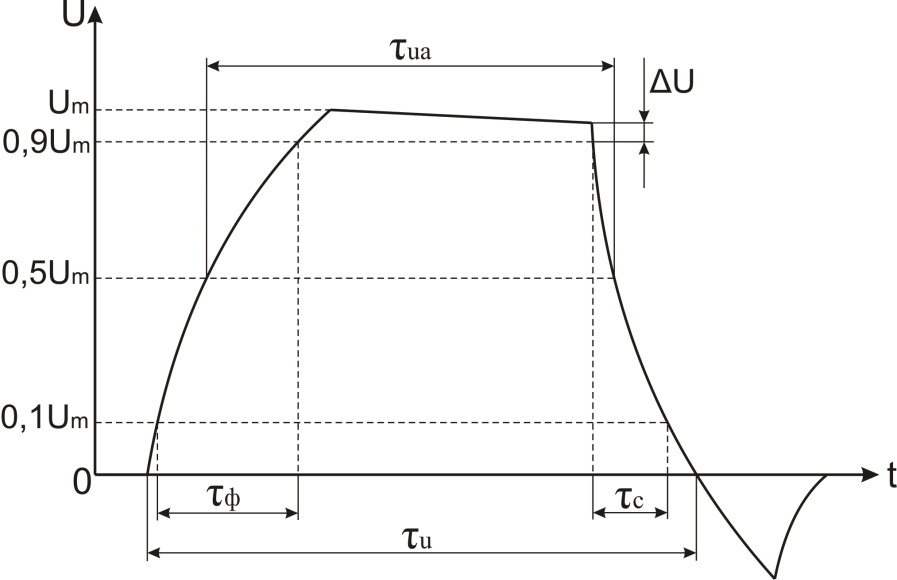
Рис. 1.7. Параметры
одиночного импульса
Форму
импульсов и свойства отдельных его
участков с количественной стороны
оценивают следующими параметрами:
-
Um
– амплитуда (наибольшее значение)
импульса. Амплитуда импульса Um
(Im)
выражается в
вольтах (амперах). -
τ
и –
длительность импульса. Обычно измерения
длительности импульсов или отдельных
участков производят на определённом
уровне от их основания. Если это не
оговаривается, то длительность импульса
определяется на нулевом уровне. Однако
чаще всего длительность импульса
определяется на уровне 0,1Um
или 0,5Um,
считая от основания. В последнем случае
длительность импульса называется
активной
длительностью и обозначается τ
иа.
При необходимости и в зависимости от
формы импульсов принятые значения
уровней для измерения специально
оговариваются.
-
τф
– длительность фронта, определяемая
временем нарастания импульса от уровня
0,1Um
до уровня 0,9Um
. -
τс
– длительность среза (заднего фронта),
определяемая временем спада импульса
от уровня 0,9Um
до уровня 0,1Um.
Когда длительность фронта или среза
измеряется на уровне 0,5Um
, она называется
активной длительностью и обозначается
добавлением индекса «а»
аналогично активной длительности
импульса. Обычно τф
и τс
составляет единицы процентов от
длительности импульса. Чем меньше τф
и τс
по
сравнению с τ
и
, тем
больше форма импульса приближается к
прямоугольной. Иногда вместо τф
и τс
фронты
импульса характеризуют скоростью
нарастания (спада). Эту величину называют
крутизной
(S)
фронта (среза)
и выражают в вольтах в секунду (В/с)
или киловольтах в секунду (кВ/с).
Для прямоугольного импульса
………………………………(1.14).
-
Участок
импульса между фронтами называют
плоской вершиной. На рис.1.7 показан спад
плоской вершины (ΔU). -
Мощность в импульсе.
Энергия W
импульса,
отнесённая к его длительности, определяет
мощность в импульсе:
………………………………(1.15).
Она выражается
в ваттах (Вт),
киловаттах (кВт)
или дольных едини-
цах ватта.
В
импульсных устройствах используются
импульсы, имеющие длительности от долей
секунды до наносекунд (10
– 9
с).
Характерными
участками импульса (рис.1.8), определяющими
его форму,
являются:
-
фронт
(1 – 2); -
вершина
(2 – 3); -
срез
(3 – 4), иногда называемый задним фронтом; -
хвост
(4 – 5).
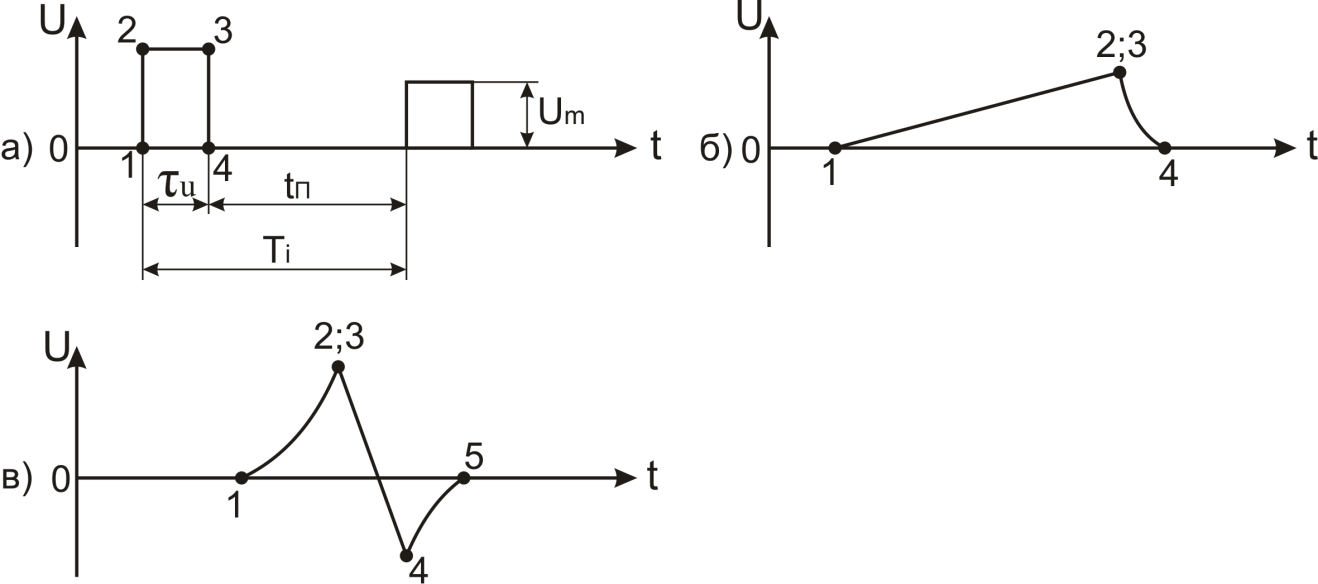
Рис.1.8.
Характерные участки импульса
Отдельные
участки у импульсов различной формы
могут отсутствовать. Следует иметь в
виду, что реальные импульсы не имеют
формы, строго соответствующей названию.
Различают импульсы положительной и
отрицательной полярности, а также
двусторонние (разнополярные) импульсы
(рис.
1.6,е).
Радиоимпульсами
называются импульсы высокочастотных
колебаний напряжения или тока обычно
синусоидальной формы. Радиоимпульсы
не имеют постоянной составляющей.
Радиоимпульсы получают модулированием
высокочастотных синусоидальных колебаний
по амплитуде. При этом амплитудная
модуляция производится по закону
управляющего видеоимпульса. Формы
соответствующих радиоимпульсов,
полученных с помощью амплитудной
модуляции, показаны на рис. 1.9:
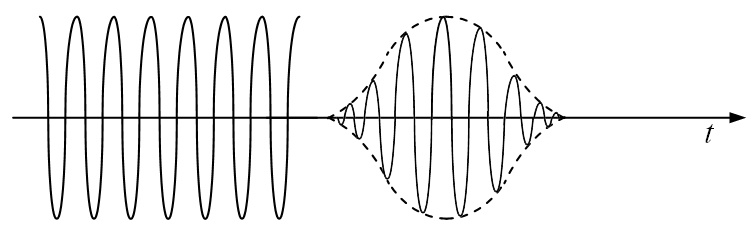
Рис.1.9.
Формы радиоимпульсов
Электрические
импульсы, следующие друг за другом через
равные промежутки времени, называются
периодической
последовательностью
(рис.1.10).
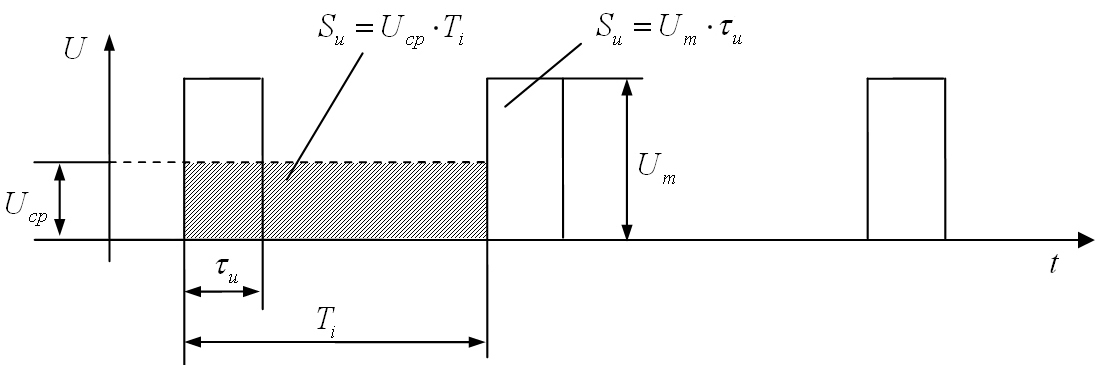
Рис.1.10. Периодическая
последовательность импульсов
Периодическая
последовательность импульсов
характеризуется следующими параметрами:
-
Период
повторения Тi
–
промежуток времени между началом двух
соседних однополярных импульсов. Он
выражается в секундах (с)
или дольных единицах секунды (мс;
мкс; нс).
Величина,
обратная периоду повторения, называется
частотой повторения (следования)
импульсов. Она определяет количество
импульсов, в течение одной секунды и
выражается в герцах (Гц),
килогерцах
(кГц)
и т.д.
………………………………..
(1.16)
-
Скважность
последовательности импульсов – это
отношение периода повторения к
длительности импульса. Обозначается
буквой q:
………………… (1.17)
Скважность
– безразмерная величина, которая может
изменяться в очень широких пределах,
так как длительность импульсов может
быть в сотни и даже тысячи раз меньше
периода импульсов или, наоборот, занимать
большую часть периода.
Величина,
обратная скважности, называется
коэффициентом заполнения. Эта величина
безразмерная, меньшая единицы. Она
обозначается буквой γ:
…………………………(1.18)
Последовательность
импульсов с q
= 2 называется
«меандром».
У такой
последовательности
(рис.1.6,е).
Если Тi
>>
τи,
то такая последовательность называется
радиолокационной.
-
Среднее
значение (постоянная составляющая)
импульсного колебания. При определении
среднего за период значения импульсного
колебания Uср
(или Іср)
импульс напряжения или тока распределяют
равномерно на весь период так, чтобы
площадь Uср
·Тi
была
равна площади импульса Sи
= Um
·
τи
(рис.
1.10).
Для
импульсов любой формы среднее значение
определяется из выражения
……………………(1.19),
где
U(t)
– аналитическое выражение формы
импульса.
Для
периодической последовательности
импульсов прямоугольной формы, у которой
U(t)
= Um
, период
повторения Тi
и
длительность импульса
τи,
это выражение
после подстановки и преобразования
принимает вид:
…………………….(1.20).
Из
рис. 1.10 видно, что Sи
= Um
·
τи
= Uср·Тi
, откуда
следует:
……………(1.21),
где
U0
– называется
постоянной составляющей.
Таким
образом, среднее значение (постоянная
составляющая) напряжения (тока)
последовательности прямоугольных
импульсов в q
раз меньше
амплитуды импульса.
-
Средняя
мощность последовательности импульсов.
Энергия импульса W,
отнесённая к периоду Тi
, определяет
среднюю мощность импульса
……………………………..
(1.22).
Сравнивая
выражения
Ри
и
Рср,
получим
Ри·
τи
= Рср·
Тi
,
откуда следует
…………………(1.23)
и
……………………. (1.24),
т.е.
средняя мощность и мощность в импульсе
отличаются в q
раз.
Отсюда
следует, что мощность в импульсе, которую
обеспечивает генератор, может в q
раз превосходить
среднюю мощность генератора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как связаны между собой частота колебаний и период?
Онлайн калькуляторы: перевод частоты колебаний в период и, наоборот –
перевод периода в частоту
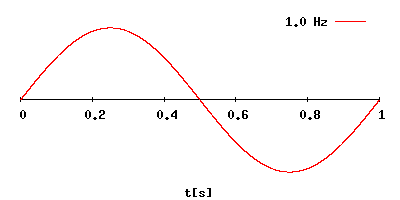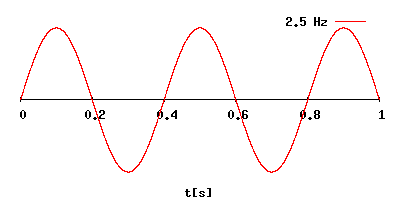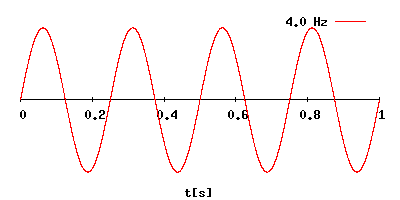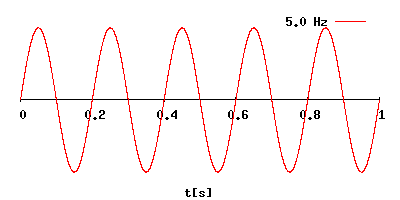
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического
(в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом:
F(Гц) = 1/T(с) и соответственно:
T(с) = 1/F(Гц)
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое может оказаться довольно громоздким,
а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим
пройденный материал парой простых онлайн калькуляторов.
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ПЕРИОДА КОЛЕБАНИЙ ПО ЧАСТОТЕ
Частота колебаний F |
||
Период Т |
А теперь всё то же самое, но наоборот:
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ПЕРИОДУ КОЛЕБАНИЙ
Период колебаний Т |
||
Частота F |
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина –
циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω.
В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно:
ω (рад/с) = 2πF(Гц).
Спектр периодической последовательности прямоугольных импульсов
Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите

Вводные замечания
В предыдущих разделах мы рассмотрели
разложение периодических сигналов в ряд Фурье,
а также изучили
некоторые свойства
представления периодических сигналов рядом Фурье.
Мы говорили, что периодические сигналы можно представить как ряд комплексных экспонент,
отстоящих друг от друга на частоту 
где 
В результате мы можем трактовать представление сигнала в виде ряда комплексных гармоник как комплексный спектр сигнала.
Комплексный спектр, в свою очередь, может быть разделен на амплитудный и фазовый спектры периодического сигнала.
В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов,
как одного из важнейших сигналов, используемого в практических приложениях.
Спектр периодической последовательности прямоугольных импульсов
Пусть входной сигнал 
прямоугольных импульсов амплитуды 

периодом 

Рисунок 1. Периодическая последовательность прямоугольных импульсов
Единица измерения амплитуды сигнала 
физического процесса, который описывает сигнал 
Это может быть напряжение, или, сила тока,
или любая другая физическая величина со своей единицей измерения,
которая меняется во времени как 
При этом, единицы измерения амплитуд спектра


будут совпадать с единицами
измерения амплитуды 
Тогда спектр 

данного сигнала может быть представлен как:
(1)
Спектр периодической последовательности прямоугольных импульсов представляет собой множество гармоник с огибающей вида

Свойства спектра периодической последовательности прямоугольных импульсов
Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.
Постоянная составляющая огибающей 
(2)
Для раскрытия неопределенности воспользуемся правилом Лопиталя [1, стр. 257]:
(3)
где 
периода повторения импульсов к длительности одиночного импульса.
Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность.
При увеличении скважности (т.е. при уменьшении длительности импульса при
фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.
Используя скважность импульсов выражение (1) можно переписать в виде:
(4)
где 
Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:
(5)
Знаменатель обращается в ноль только при 

(6)
Тогда огибающая обращается в ноль если
(7)
На рисунке 2 показана огибающая спектра периодической последовательности
прямоугольных импульсов 
соотношения огибающей и дискретного спектра 

Рисунок 2. Cпектр периодической последовательности
прямоугольных импульсов
Также показаны амплитудная огибающая 



Из рисунка 2 можно заметить, что фазовый спектр 
когда огибающая 
Заметим, что 

той же точке комплексной плоскости равной 
Пример спектра периодической последовательности прямоугольных импульсов
Пусть входной сигнал 
прямоугольных импульсов амплитуды 

и различной скважностью 
На рисунке 3а показаны временные осциллограммы указанных сигналов,
их амплитудные спектры 
а также непрерывные огибающие 

Рисунок 3. Cпектр периодической последовательности
прямоугольных импульсов при различном значении скважности
а — временные осциллограммы; б — амплитудный спектр
Как можно видеть из рисунка 3, при увеличении скважности сигнала, длительность импульсов 
огибающая спектра 
В результате, в пределах главного лепестка увеличивается количество гармоник спектра 
Спектр смещенной во времени периодической последовательности прямоугольных импульсов
Выше мы подробно изучили спектр периодической последовательности прямоугольных
импульсов для случая, когда исходный сигнал 

В результате спектр такого сигнала 
Теперь мы рассмотрим, что произойдет со спектром сигнала
если мы сместим сигнал 

Рисунок 4. Сдвинутая во времени периодическая последовательность прямоугольных импульсов
Смещенный сигнал 

задержанный на половину длительности импульса

Спектр 

согласно свойству
циклического временного сдвига
как:
(8)
Таким образом, спектр периодической последовательности прямоугольных импульсов, смещенной относительно нуля, не
является чисто вещественной функцией, а приобретает дополнительный фазовый множитель

Амплитудный 
спектры показаны на рисунке 5.

Рисунок 5. Амплитудный и фазовый спектры сдвинутой во времени периодической
последовательности прямоугольных импульсов
Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала,
но добавляет линейную составляющую к фазовому спектру сигнала.
Выводы
В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.
Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры
спектров при различном значении скважности.
Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано,
что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.
Программная реализация в библиотеке DSPL
Данные для построения рисунков данного раздела были просчитаны при использовании
библиотеки DSPL-2.0
Ниже приведён исходный код программы расчета данных для построения рисунка 3:
fourier_series_pimp_q.c
#include <stdio.h>
#include <string.h>
#include "dspl.h"
/* Размер векторов входных сигналов и огибающей спетра */
#define N 1000
/* Период повторения импульса. Для изменения скважности мы будем менять
* длительность импульса при фиксированном периоде повторения */
#define T 4.0
/* Амплитуда */
#define A 2.0
/* Количество спектральных гармоник разложения в ряд Фурье */
#define M 41
/* длина команды Gnuplot */
#define PLOTCMD_LEN 256
int main(int argc, char* argv[])
{
double t1[N]; /* время (сек) на одном периоде повторения */
double t4[N]; /* время (сек) на четырех периодах повторения */
double s[N]; /* входной сигнал */
complex_t S[M]; /* комплексный спектр периодического сигнала */
double Smag[M]; /* амплитудный спектр периодического сигнала */
double w[M]; /* частота (рад/c) дискретного спектра */
double wc[N]; /* частота (рад/с) огибающей спектра */
double Sc[N]; /* огибающая спектра */
double tau; /* длительность импульса */
/* скважность */
double Q[3] = {5.0, 2.0, 1.25};
int q, m, n;
char fname[64]; /* имя файла данных */
char plotcmd[PLOTCMD_LEN]; /* Команда Gnuplot */
void* hdspl; /* DSPL handle */
void* hplot; /* GNUPLOT handle */
hdspl = dspl_load();
if(!hdspl)
{
printf("Cannot to load libdspl!n");
return 0;
}
/* Вектор частот непрерывной огибаюхей вида sin(w/2*tau) / (w/2*T) */
linspace(-M_PI*(double)M/(double)T, M_PI*(double)M/(double)T, N, DSPL_SYMMETRIC, wc);
/* заполнение массива временных отсчетов */
/* на одном периоде повторения сигнала */
linspace(-T/2.0, T/2.0, N, DSPL_PERIODIC, t1);
/* заполнение массива временных отсчетов
* на 4-x периодах повторения сигнала
* для отображения на осциллограмме */
linspace(-T*2.0, T*2.0, N, DSPL_PERIODIC, t4);
/* Построение графиков пакетом GNUPLOT */
gnuplot_create(argc, argv, 800, 640, "img/fourier_series_rec.png", &hplot);
gnuplot_cmd(hplot, "unset key");
gnuplot_cmd(hplot, "set multiplot layout 3,2 rowsfirst");
gnuplot_cmd(hplot, "set yrange [0:2.2]");
for(q = 0; q < 3; q++)
{
tau = T/Q[q];
/* 4 периода повторения п-импульса скважности Q[q] */
signal_pimp(t4, N, A, tau, 0.0, T, s);
/* сохранение в текстовый файл временных осциллограмм */
sprintf(fname, "dat/pimp_time_%.2lf.csv", Q[q]);
writetxt(t4, s, N, fname);
/* Построение временнОй осциллограммы */
sprintf(plotcmd, "plot '%s' with lines", fname);
gnuplot_cmd(hplot, plotcmd);
/* один период повторения п-импульса скважности Q[q] */
signal_pimp(t1, N, A, tau, 0.0, T, s);
/* разложение в ряд Фурье */
fourier_series_dec(t1, s, N, T, M, w, S);
/* Рассчет амплитудного спектра */
for(m = 0; m < M; m++)
{
/*printf("S[%d] = %f %fn", m, RE(S[m]), IM(S[m]));*/
Smag[m] = ABS(S[m]);
}
/* Сохранение в файл амплитудного спетра для скважности Q[q] */
sprintf(fname, "dat/pimp_freq_discrete_%.2lf.csv", Q[q]);
writetxt(w, Smag, M, fname);
/* Построение на график амплитудного спектра для заданной скважности */
sprintf(plotcmd, "plot '%s' with impulses lt 1 ,\", fname);
printf("%sn", plotcmd);
gnuplot_cmd(hplot, plotcmd);
sprintf(plotcmd, "'%s' with points pt 7 ps 0.5 lt 1 ,\", fname);
printf("%sn", plotcmd);
gnuplot_cmd(hplot, plotcmd);
/* Расчет огибающей */
for(n = 0; n < N; n++)
Sc[n] = (wc[n] == 0.0) ? A/Q[q] : fabs( A * sin(0.5*wc[n]*tau) / (0.5*wc[n] * T));
/* сохранение огибающей в файл для скважности Q[q] */
sprintf(fname, "dat/pimp_freq_cont_%.2lf.csv", Q[q]);
writetxt(wc, Sc, N, fname);
/* Построение на график непрерывной огибающей
амплитудного спектра для заданной скважности */
sprintf(plotcmd, "'%s' with lines", fname);
printf("%sn", plotcmd);
gnuplot_cmd(hplot, plotcmd);
}
gnuplot_cmd(hplot, "unset multiplot");
gnuplot_close(hplot);
/* remember to free the resource */
dspl_free(hdspl);
return 0;
}
Смотри также
Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье
Список литературы
[1]
Основы математического анализа.
Москва, Наука, 1965, 572 c.
[2]
Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[3]
Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.
[4]
Дёч, Г.
Руководство по практическому применению преобразования Лапласа.
Москва, Наука, 1965, 288 c.
[5]
Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6
Последнее изменение страницы: 12.05.2022 (19:42:36)
Страница создана Latex to HTML translator ver. 5.20.11.14