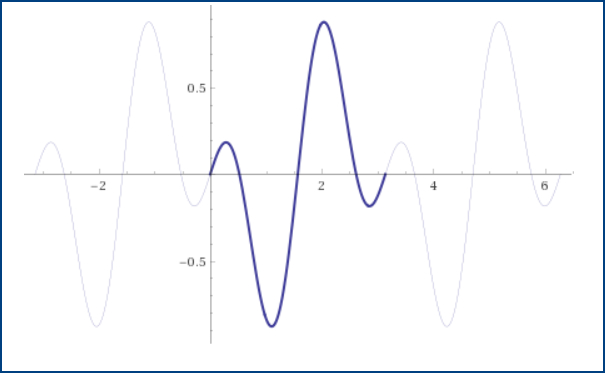
Типичная школьная задача — нахождение периода функции. Теперь вы можете решить эту быстро онлайн с помощью нашего калькулятора. Для это надо только ввести команду «period» и функцию для которой надо найти период. Кроме того что будет выведен период, если он есть, будет еще и график построен (как на рисунке слева) на котором будет показана величина периода.
Чтобы воспользоваться онлайн сервисом нажмите значок копирования, чтобы добавить команду из примера в окно ввода команд для обработки изображений.
Пример команды, которая находит период функции одной переменной. Ключевое слово — «period».
period y=sin(x)*cos(3x)
Пример команды, которая позволяет найти период функции двух переменных. Период определяется для каждой переменной отдельно.
period of f(x,y)=sin(x)*cos(3y)
Пример функции у которой нет периода (будет выведено сообщение «function not periodic»).
period y=sin(x)*cos(3x)+x^2
Пишите в комментарии примеры функция для которых вы нашли период с помощью нашего калькулятора.
Похожие публикации
2019-11-01 • Просмотров [ 46173 ]
Задача 12011 Найти период функции у =…
Условие
Найти период функции у = sin(3x/2)+ctg(5x/3)-cosx(2x+2)-3tg((4x-5)/3)
математика 10-11 класс
4539
Решение
Если период функции f(x) равен Т, то период функции f(kx) равен Т/k.
Если период функции f(x) равен T1, а период функции g(x) равен Т2, то период функции f(x)±g(x) равен наименьшему числу T, при делении которого на Т1 и Т2 получаются целые числа.
T1=(2π)/(3/2)=4π/3;
Т2=π/(5/3)=3π/5;
Т3=2π/2=π;
Т4=π/(4/3))=3π/4
Т=12π
Т:Т1=9
Т:Т2=20
Т:Т3=12
Т:Т4=16
Ответ: 12π
Написать комментарий
Онлайн калькулятор для определения периодичности функции. Периодическая функция — это функция повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции) на всей области определения.
Периодичная функция может иметь и несколько периодов, самый маленький положительный из них называется основным.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Y = sin x
T = 2π (T-период)
y = asin kx
T= (от а не зависит)
y = sin 3x
T=
Думаю теперь понятно как находить период такой функции
А вот как находить период суммы, произведения и частного функций
y = f(ax) + f(bx) — основные периоды соизмеримы
T = НОК(T₁; T₂ )
y = 2 sin (x/3) · 4 cos 5x
T₁ = T₂ =
T = НОК(6π; 2π/5) = 6π
если периоды не соизмеримы (нужно искать НОК разных иррациональных чисел) то функция суммы произведения частного не имеет периода
Алгебра
Митуля
30 августа, 08:20
+2
Ответы (1)
-
Настасьюшка
30 августа, 09:07
0
Период функции y=sinx равен 2 π
Период функции y=sin3x равен 2π/3
- Комментировать
- Жалоба
- Ссылка
Знаешь ответ?
Не уверен в ответе?
Найди верный ответ на вопрос ✅ «Период функции y=sin3x …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по алгебре
Периметр прямоугольника 6,6 дм. Одна сторона больше другой на 0,9 дм. найдите площадь прямоугольника.
Ответы (1)
Как решить систему уровнений x-y=17 3x-4y=-12
Ответы (1)
x (x+2) (5x-1) = 0
Ответы (1)
Турист проплыл по течению 240 км, затратив на этот путь 12 часов, при этом скорость течения равнялась 3 км/ч. Далее он продолжил путь по озеру, затратив на весь путь по нему 4 часа. Найдите расстояние, которое турист проплыл по озеру.
Ответы (2)
Решите систему уравнений 5y-6x=4 7x-4y=-1
Ответы (1)