Как найти период суммы двух функций

Спасибо за ответ. То есть если у меня две функции и , то период первой равен , а второй . После приведения к общему знаменателю, 6, числители равны 4 и 3 соответственно НОК(4,3)=12. Следовательно, период суммы равен .

Suppose that period of $f(x)=T$ and period of $g(x)=S$, I am interested what is a period of $f(x) g(x)$? period of $f(x)+g(x)$? What I have tried is to search in internet, and found following link for this.

Also I know that period of $sin(x)$ is $2pi$, but what about $sin^2(x)$? Does it have period again $pi n$, or? example is following function
$y=frac{sin^2(x)}{cos(x)}$
i can do following thing, namely we know that $sin(x)/cos(x)=tan(x)$ and period of tangent function is $pi$, so I can represent
$y=sin^2(x)/cos(x)$ as $y=tan(x)timessin(x)$,but how can calculate period of this?

Please help me.

УДК 517.17+517,51

ПЕРИОД СУММЫ ДВУХ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ

А/О. Эвнин

В работе полностью решен вопрос, каким может быть основной период периодической функции, являющейся суммой двух периодических функций с известными основными периодами. Изучается также случай отсутствия основного периода у периодической суммы периодических функций.

Мы рассматриваем действительнозначные функции действительного переменного. В энциклопедическом издании [1] в статье «Периодические функции» можно прочитать: «Сумма периодических функций с разными периодами является периодической только тогда, когда их периоды соизмеримы». Это утверждение справедливо для непрерывных функций1, но не имеет места в общем случае. Контрпример весьма общего вида был построен в [4]. В данной статье мы выясняем, каким может быть основной период периодической функции, являющейся суммой двух периодических функций с известными основными периодами.

Предварительные сведения

Напомним, что функция / называется периодической, если для некоторого числа Т Ф О при любом х из области определения D(f) числа х + Т и х — Т принадлежат D(f) и выполняются равенства f(x + T) =f(x) =f(x ~ Т). При этом число Г называют периодом функции.

Наименьший положительный период функции (если, конечно, он существует) будем называть основным периодом. Известен следующий факт.

Теорема 1. Если у функции есть основной период То, то любой период функции имеет вид пТо, где п Ф 0 — целое число.

Числа Т и Т2 называют соизмеримыми, если существует такое число Т0, которое целое число раз «укладывается» и в Т, и в Т2: Т = Т2 = п2Т0, щ,п2е Z. В противном случае числа Т и Т2 называют несоизмеримыми. Соизмеримость (несоизмеримость) периодов означает, таким образом, что их отношение есть число рациональное (иррациональное).

Из теоремы 1 следует, что у функции, имеющей основной период, любые два периода соизмеримы.

Классическим примером функции, не имеющей наименьшего периода, является функция Дирихле, равная 1 в рациональных точках, и нулю — в иррациональных. Любое рациональное число, отличное от нуля, является периодом функции Дирихле, а любое иррациональное число не является ее периодом. Как видим, и здесь любые два периода соизмеримы.

Приведем пример непостоянной периодической функции, имеющей несоизмеримые периоды.

Пусть функция /(х) в точках вида /и + ла/2, m, п е Z, равна 1, а в остальных точках равна

нулю. Среди периодов этой функции есть 1 и л

Период суммы функций с соизмеримыми периодами

Теорема 2. Пусть fug- периодические функции с основными периодами тТ0 и «То, где тип

mnj

— взаимно простые числа. Тогда основной период их суммы (если он существует), равен —

к

где к — натуральное число, взаимно простое с числом тп.

Доказательство. Пусть h = / + g. Очевидно, что число тпТ0 является периодом h. В силу

тпр

теоремы 1 основной период h имеет вид-где к- некоторое натуральное число. Предполо-

к

жим, что к не является взаимно простым с числом m, то есть к — dku m = dm, где d> 1 — наи-

1 Красивое доказательство того, что сумма любого конечного числа непрерывных функций с попарно несоизмеримыми периодами непериодична, содержится в статье [2] См. также [3].

больший общий делитель чисел т и к. Тогда период функции к равен

а функция f=h-g

имеет период mxnTо, не являющийся кратным ее основного периода mTQ. Получено противоречие с теоремой 1. Значит, к взаимно просто с т. Аналогично, взаимно простыми являются числа к и п. Таким образом, А: взаимно просто с тп. □

Теорема 3. Пусть т, п и к ~ попарно взаимно простые числа, а Т0 — положительное число. Тогда существуют такие периодические функции fug, что основные периоды f, g и (f + g) рае-

тппТ

ны соответственно тТ$, nTQ и-

к

Доказательство. Доказательство теоремы будет конструктивным: мы просто построим соответствующий пример. Предварительно сформулируем следующий результат. Утверждение. Пусть т — взаимно простые числа. Тогда функции

fx — cos— + cos-—- и f2= cos— m n m

cos— имеют основным периодом число 2ктп. п

Доказательство утверждения. Очевидно, что число 2птп является периодом обеих функций. Легко можно проверить, что этот период основной для функции Найдем ее точки максимума.

х=1 ,

Х-2 5GZ

/,(*) = 2о<

cos— = 1 т

о

х 1

cos— -1

п

х = 2лМ, te Z.

Имеем = п!. Из взаимной простоты тип следует, что 5 кратно /г, т.е. я = I е Ъ . Значит, /х(х) = 2 о х = 2тстп1,1 е 2, а расстояние между соседними точками максимума функции / равно 2ктп, и положительный период/1 не может быть меньше числа 2 шпп.

Для функции^ применим рассуждения другого рода (которые подходят и для функции/ь но

2ктп

менее элементарны). Как показывает теорема 1, основной период Г функции/2 имеет вид -,

где к- некоторое натуральное число, взаимно простое с тип. Число Гбудет и периодом функции

( 2 ^ 2 хп г т т /2 + /2 = — -1 cos

V

п

J

п

все периоды которой имеют вид 2пп1. Итак,

2ктп

2nnl, т.е. т = kl. Так как т и к взаимно про-

сты, отсюда следует, что к= 1.

Теперь для доказательства теоремы 3 можно построить искомый пример. Пример. Пусть т, п и к — попарно взаимно простые числа и хотя бы одно из чисел п или к отлично от 1. Тогда пф к ив силу доказанного утверждения функции

/ (х) = cos-—- + cos— т к

. X X

И g(x) = cos—cos — п к

имеют основные периоды 2 лтк и 2 тк соответственно, а у их суммы

к(х) = f(x) + = cos— + cos—

m n

основной период равен 2 ттп.

Если же п = к = 1, то подойдет пара функций

х

f{x)-2 cos— + COS X и g(x) — COS X. m

Их основные периоды, а также период функции к(х) — 2 равны соответственно 2лм, 2/ги 2тип.

( X cos— + COS X

m J

как легко проверить.

Математика

Обозначим Т = 2лк. Для произвольных попарно взаимно простых чисел тп, п и к указаны функции/и £ такие, что основные периоды функций/, g и/ + g равны соответственно тТ, пТ и

. Условию теоремы удовлетворяют функции / — л;

V^o j

и g

-X

Т0 J

Период суммы функций с несоизмеримыми периодами

Следующее утверждение почти очевидно.

Теорема 4. Пусть fug- периодические функции с несоизмеримыми основными периодами Т} и Т2, а сумма этих функций h = f + g периодична и имеет основной период Т. Тогда число Т несоизмеримо ни с Т], ни с Т2.

Доказательство. С одной стороны, если числа ТнТ} соизмеримы, то функция g = h-f имеет период, соизмеримый с Г]. С другой стороны, в силу теоремы 1 любой период функции g кратен числу Т2. Получаем противоречие с несоизмеримостью чисел Т и Т2. Несоизмеримость чисел Т и Т2 доказывается аналогично, d

Замечательным, и даже в некотором роде удивительным, является тот факт, что справедливо и утверждение, обратное к теореме 4. Широко распространено заблуждение о том, что сумма двух периодических функций с несоизмеримыми периодами не может быть функцией периодической. На самом же деле это не так. Более того, период суммы может быть любым положительным числом, удовлетворяющим утверждению теоремы 4.

Теорема 5. Пусть Т, Т2иТ~ попарно несоизмеримые положительные числа. Тогда существуют такие периодические функции fug, что их сумма h =/+ g периодична, а основные периоды функцииf guhравны соответственно Th Т2 и Т.

Доказательство. Доказательство вновь будет конструктивным. Наши построения будут существенно зависеть от того, представимо или не представимо число Т в виде рациональной комбинации Т = аТ + рТ2 (а и Р — рациональные числа) периодов Т и Т2.

I. Т не является рациональной комбинацией Тг и J2-

Пусть А = {mT + пТ2 + kTm,n, k е Z} — множество целых линейных комбинаций чисел Гь Т2 и Т. Отметим сразу, что если число представимо в виде пгТ + пТ2 + кТ, то такое представление единственно. Действительно, если тхТ + пТг + кТ- m2Tx + п2Т2 + к2Т9 то

(к} — к2)Т- (от2 — т)Т] + (п2 — щ)Тъ и при к * к2 получаем, что Т рационально выражается через Т] и Т2. Значит, к = к2. Теперь из несоизмеримости чисел Т и Т2 непосредственно получаются равенства т = т2 и щ = п2.

Важным является тот легко проверяемый факт, что множества А и дополнение к нему А замкнуты относительно прибавления чисел из А: если х е А и у е А, то х + у е А; если х е А и у е А, тох + у е А.

Положим, что во всех точках множества А функции/и g равны нулю, а на множестве А зададим эти функции следующим образом:

f(mTi + пТ2 + кТ) = пТ2 + кТ g(mT1 + пТ2 + кТ) — гпТ — кТ.

Поскольку, как было показано, по числу х е А коэффициенты т,пик линейной комбинации периодов Гь Т2 и Г восстанавливаются однозначно, указанные задания функций/и g корректны.

Функция h =/ + g на множестве А равна нулю, а в точках множества А равна

h(mT + пТ2 + кТ) — тТ + пТ2.

Непосредственной подстановкой легко убедиться, что число Т — период функции f число Т2 — период g, а Т~ период h. Покажем, что эти периоды — основные.

Сначала отметим, что любой период функции /принадлежит множеству А. Действительно,

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

если 0 фх в А,у е А, т ох + у е А и f(x + у) = 0 *f(x). Значит, у е А — не период функции /

Пусть теперь не равные друг другу числах, х2 принадлежат^ и f(x 1) ~f(x2). Из определения функции / отсюда получаем, что х — х2 = 1ТЬ где I- некоторое ненулевое целое число. Стало быть, любой период функции/кратен Т. Таким образом, Тх — действительно основной период/

Точно так же проверяются утверждения относительно Т2 и Т.

Замечание. В книге [4] на с. 172-173 приводится другая общая конструкция для случая I.

II. Т- рациональная комбинация Т и Т2.

Представим рациональную комбинацию периодов Т и Т2 в виде Г = — (кхТх + к2Т2), где кх и

Я

к2 ™ взаимно простые целые числа, к{Г + к2Т2 > 0, а/? и д — натуральные числа. Введем в рассмотри, лeZ>.

тТх+ пТ2

рение множество В——

I ?

Положим, что во всех точках множества В функцииfиg равны нулю, а на множестве В зададим эти функции следующим образом:

/

g

^ тТ + пТ2 Л Я

^ mTx + пТ2 Л

9

<«2

m

Р

m

h

Здесь, как обычно, [х] и {х} обозначают соответственно целую и дробную часть числах. Функция к =/+ д на множестве В равна нулю, а в точках множества В равна

h

fmTx +пТ: л Ч

п m

_Р_

+

Т2

J

‘2 Л1

Непосредственной подстановкой несложно проверить, что число Тх — период функции/, число Т2 — период g, а Т- период h. Покажем, что эти периоды — основные.

Любой период функции / принадлежит множеству В. Действительно, если 0 * х е В, у е В, то f(x) Ф 0, j{x + у) = 0 */(*)■ Значит, у е В _ Не период функции/

Итак, всякий период функции / имеет вид Ту =

, где 5i и 52 — целые числа. Пусть

777

х =—7] 4- —Г2, х е 5. Если я = 0, то /(я) — рациональное число. Теперь из рациональности числа /(х + 7}) вытекает равенство -I — I — 0. Значит, имеем равенство 52 = Хр, где X — некоторое целое

[Р)

число. Соотношение/(х + 7}) = /(х) принимает вид

О)

^ П + I + I ш +

к2 1 Я 1 1 Ч

Данное равенство должно выполняться при всех целых тип. При т-п~ 0 правая часть (1) рав-

Я

на нулю. Поскольку дробные части неотрицательны, получаем отсюда, что —<0, а при

к2

т = п = д — ] сумма дробных частей в правой части равенства (1) не меньше суммы дробных час-X

тей слева. Значит, — >0. Таким образом, X = 0 и 52 = 0. Поэтому период функции / имеет вид

Тг =

sT

а равенство (1) переходит в

п | [w + Jij^fwl | т

(2)

Математика

При т-п~ 0 получаем I — > = О, т.е. делится на д, а любой период функции/кратен Гь Дока-

Ы

зано, что Т — основной период функции/

Аналогичные рассуждения применимы и к функции g.

Перейдем теперь к функции к. Так же, как и выше, устанавливаем, что период функции к

должен быть вида Тн — ^ + , где 5] и 52 — целые числа. Из соотношений

Ч

й(0) = 0 = й(ГА) =

52 Л

.Р J .Р.

к2 кх

¡2

(3)

ч.Л IР^

получаем, что числа 51 и ^ должны быть кратны р, т.е. при некоторых целых Лх и Л2 имеем 51 = Лр, Э2 = Л2р. Тогда соотношение (3) можно переписать в виде

к2 к{

Из равенства Л2кх = к2Л и взаимной простоты чисел к и к2, вытекает, что Л2 делится на к2. Отсюда

Е я

для некоторого целого числа t справедливы равенства Л2 = k2t и Лх ~ kxt, т.е. Th ~—{кхТх + к2Т2).

Показано, что любой период функции h кратен периоду Т = — (к{Гх + к2Т2)9 который, таким обра-

Ч

зом, является основным. □

Отсутствие основного периода

Теорема 6. Пусть Тх и Т2~- произвольные положительные числа. Тогда существуют такие периодические функции fug, что их основные периоды равны соответственно Т и Т2, а их сумма h=f+g периодична, но не имеет основного периода.

Доказательство. Рассмотрим два возможных случая.

I. Периоды Тх и Т2 несоизмеримы.

Пусть A = + пТ2 +kT . Как и выше, легко показать, что если число

представимо в виде тТх + пТ2 + кТ , то такое представление единственно.

Положим, что во всех точках множества А функции / и g равны нулю, а на множестве А зададим эти функции следующим образом:

/от; + пТ2 + кТ) = пТ2 + кТ, g(mTx + пТ2 + кТ) = тТх — кТ.

Несложно убедиться в том, что число Тх — основной период функции / , число Т2 — основной период g , и при любом рациональном к число кТ — период функции h — f + g, у которой, таким образом, нет наименьшего периода.

II. Периоды Тх и Т2 соизмеримы.

Пусть Тх =тТ0,Т2 = пТ0, где Т0 > О, m и п — натуральные числа. Введем в рассмотрение множество Я = + .

Положим, что во всех точках множества В функции fug равны нулю, а на множестве В зададим эти функции так:

/((/ + ЩТ0) = Щ + Jit, g((/ + 4lk)T0) — Щ — 42к.

Функция h ~ / + g на множестве В равна нулю, а в точках множества В равна

Нетрудно проверить, что число 7j = mTQ — основной период функции / , число Т2 ~ пТ0 — основной период g, в то время как среди периодов функции h~ f + g есть все числа вида л/2кТ0, где к — произвольное рациональное число. □

В основе конструкций, доказывающих теорему 6, лежит несоизмеримость периодов функции h~ / + g с периодами функций / и g . Приведем в заключение пример таких функций fug, что все периоды функций /, g и / + g соизмеримы между собой, но у / и g есть основные периоды, а у f + g — нет.

Пусть m — некоторое фиксированное натуральное число, М — множество несократимых нецелых дробей, числители которых кратны m . Положим

1, если хеМ; 1

fix)

еслихе mZ;

g(x)

—, ecnuxeZXmZ; 2

О в остальных случаях; 1, если хеМU

~,еслихе2 2

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

О, ecnnxgZ.

Тогда h(x)

[О в противном случае.

Легко видеть, что основные периоды функций fug равны соответственно m и 1, в то время как сумма / + g имеет периодом любое число вида m/n, где п — произвольное натуральное число, взаимно простое с m .

Литература

1. Математический энциклопедический словарь/Гл. ред. Ю.В. Прохоров — М.: Сов. энциклопедия, 1988.

2. Микаэлян Л.В., Седракян Н.М. О периодичности суммы периодических функций// Математическое образование. — 2000. — № 2(13). — С. 29-33.

3. Геренштейн A.B., Эвнин А.Ю. О сумме периодических функций// Математика в школе. -2002. — № 1. — С. 68-72.

4. Ивлев Б.М. и др. Сборник задач по алгебре и началам анализа для 9 и 10 кл. — М.: Просвещение, 1978.

Поступила в редакцию 18 августа 2004 г.

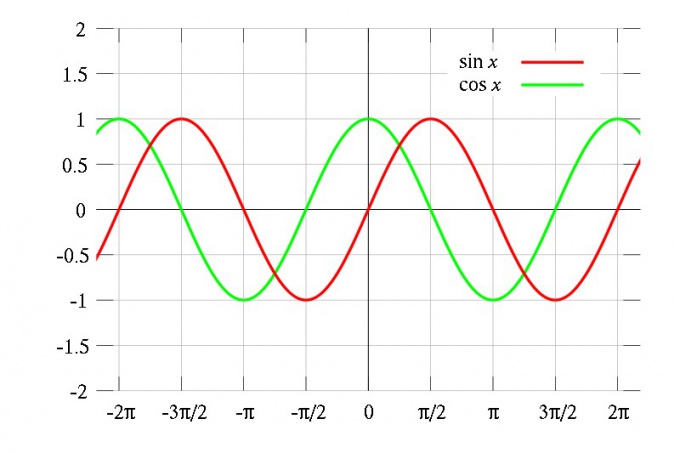
С периодическими функциями мы встречаемся в школьном курсе алгебры. Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем этот паттерн на всей области определения функции. Например,  — периодические функции.

Дадим определение периодической функции:

Функция называется периодической, если существует такое число , не равное нулю, что для любого из ее области определения

Другими словами, это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого фиксированного ненулевого числа . Число называется периодом функции. Как правило, говоря о периоде, мы имеем в виду наименьший положительный период функции.

Например, — периодические функции.

Для функций и период ,

Для функций и период

Но не только тригонометрические функции являются периодическими. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задачи:

1. Периодическая функция определена для всех действительных чисел. Ее период равен двум и Найдите значение выражения

График функции может выглядеть, например, вот так:

Отметим точку М (1; 5), принадлежащую графику функции . Поскольку период функции равен 2, значения функции в точках будут также равны пяти. Здесь k — целое число.

Как ведет себя функция в других точках — мы не знаем. Но знаем, что ее график состоит из повторяющихся элементов длиной 2, что и нарисовано.

Значения функции в точках -3 и 7 равны пяти. Мы получим:

2. График четной периодической функции совпадает с графиком функции  на отрезке от 0 до 1; период функции равен 2. Постройте график функции и найдите f(4 ).

Построим график функции при

Поскольку функция четная, ее график симметричен относительно оси ординат. Построим часть графика при симметричную части графика от 0 до 1.

Период функции равен 2. Повторим периодически участок длины 2, который уже построен.

Найдем

3. Найдите наименьший положительный период функции

Наименьший положительный период функции равен

График функции получается из графика функции сжатием в 3 раза по оси X (смотри тему «Преобразование графиков функций).

Значит, у функции частота в 3 раза больше, чем у функции , а наименьший положительный период в 3 раза меньше и равен . Значит, на отрезке укладывается ровно 3 полных волны функции

Рассуждая аналогично, получим, что для функции наименьший положительный период равен На отрезке укладывается ровно 5 полных волн функции

Числа 3 и 5 — взаимно простые. Поэтому наименьший положительный период функции равен .

4. Период функции равен 12, а период функции равен 8. Найдите наименьший положительный период функции

По условию, период функции равен 12. Это значит, что все значения повторяются через 12, через . Если мы выберем любую точку на графике функции то через значение функции будет такое же, как и в точке

Аналогично, все значения функции повторяются через . В этих точках значения будут такие же, как и в точке

На каком же расстоянии от точки расположена точка, в которой значение функции такое же, что и в точке ? Очевидно, на расстоянии Это значит, что число делится и на 12, и на 8, то есть является их наименьшим общим кратным. Значит, .

Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых. 

Как определить периодичность функции

По школьным урокам математики каждый помнит график синуса, равномерными волнами уходящий вдаль. Аналогичным свойством — повторяться через определенный промежуток — обладают и многие другие функции. Они называются периодическими. Периодичность — очень важное свойство функции, часто встречающееся в различных задачах. Поэтому полезно уметь определять, является ли функция периодической.

Инструкция

Если F(x) — функция аргумента x, то она называется периодической, если есть такое число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.

Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.

Обычно математика интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.

Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.

Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.

Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку первообразная периодически повторяется, то должна повторяться и производная. Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.

Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете график функции по горизонтали именно в столько раз

Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.

Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или поздно (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.

Однако если соотношение периодов иррационально, то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.

Источники:

• Теоретические сведения о функциях

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?